| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
.anchy.
Forumaš(ica)

Pridružen/a: 14. 11. 2007. (20:03:46)
Postovi: (1BC)16
Lokacija: Zgb
|
 Postano: 10:55 ned, 8. 1. 2012 Naslov: Postano: 10:55 ned, 8. 1. 2012 Naslov: |
    |
|
|
@Megy Poe: pa vidiš da je u tablicama [latex]L(sin(kt))=\frac{k}{s^2+k^2}[/latex]
Znači,tebi fali k u brojniku,pa jednostavno pomnožiš sa [latex]\frac{2}{2}[/latex], i dvojku staviš u brojnik,a [latex]\frac{1}{2}[/latex] izlučiš ispred Laplace-a i dobiješ [latex]\frac{1}{2}sin(2t)[/latex]
edit:može netko objasniti postupak kako dobimo Jordnaovu bazu kod matrica kojima je npr dimenzija svojstvenog potprostora 2,a geometrijska kratnost sv.vrijednosti 3?
Primjer iz vježbi,
[latex]A=\begin{bmatrix} 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \\ -2 & 2 & -3 & 1 \\ 2 & -2 & 1 & -3 \end{bmatrix}[/latex]
karakteristični polinom je [latex]k_A(\lambda)=\lambda(\lambda+2)^3[/latex]
[latex]v_0=(1,1,0,0)[/latex]
Dobili smo da je baza svoj.potprostora za -2 [latex]\{(1,0,-2,0),(0,1,0,-2)\}[/latex].
Sada mi nije dalje jasno kako smo dobili [latex]v_1,v_2,v_3[/latex] :?:
@Megy Poe: pa vidiš da je u tablicama 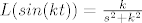
Znači,tebi fali k u brojniku,pa jednostavno pomnožiš sa 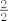 , i dvojku staviš u brojnik,a , i dvojku staviš u brojnik,a 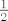 izlučiš ispred Laplace-a i dobiješ izlučiš ispred Laplace-a i dobiješ 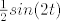
edit:može netko objasniti postupak kako dobimo Jordnaovu bazu kod matrica kojima je npr dimenzija svojstvenog potprostora 2,a geometrijska kratnost sv.vrijednosti 3?
Primjer iz vježbi,
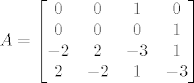
karakteristični polinom je 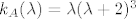
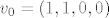
Dobili smo da je baza svoj.potprostora za -2 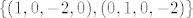 . .
Sada mi nije dalje jasno kako smo dobili 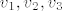 
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
.anchy.
Forumaš(ica)

Pridružen/a: 14. 11. 2007. (20:03:46)
Postovi: (1BC)16
Lokacija: Zgb
|
|
| [Vrh] |
|
Gost
|
 Postano: 13:59 ned, 8. 1. 2012 Naslov: Postano: 13:59 ned, 8. 1. 2012 Naslov: |
    |
|
|
[quote=".anchy."]@Megy Poe: pa vidiš da je u tablicama [latex]L(sin(kt))=\frac{k}{s^2+k^2}[/latex]
Znači,tebi fali k u brojniku,pa jednostavno pomnožiš sa [latex]\frac{2}{2}[/latex], i dvojku staviš u brojnik,a [latex]\frac{1}{2}[/latex] izlučiš ispred Laplace-a i dobiješ [latex]\frac{1}{2}sin(2t)[/latex]
edit:može netko objasniti postupak kako dobimo Jordnaovu bazu kod matrica kojima je npr dimenzija svojstvenog potprostora 2,a geometrijska kratnost sv.vrijednosti 3?
Primjer iz vježbi,
[latex]A=\begin{bmatrix} 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \\ -2 & 2 & -3 & 1 \\ 2 & -2 & 1 & -3 \end{bmatrix}[/latex]
karakteristični polinom je [latex]k_A(\lambda)=\lambda(\lambda+2)^3[/latex]
[latex]v_0=(1,1,0,0)[/latex]
Dobili smo da je baza svoj.potprostora za -2 [latex]\{(1,0,-2,0),(0,1,0,-2)\}[/latex].
Sada mi nije dalje jasno kako smo dobili [latex]v_1,v_2,v_3[/latex] :?:[/quote]
Ja sam baš htjela postaviti pitanje za taj primjer matrice.
ja sam to išla računat preko :
Av1=0
Av2=-2v2+v3
Av3=-2v3
Av4=-2v4
i iz toga dobim da je su mi sv vektori = (1,1,0,0),(1,0,-2,0),(0,1,0,-2),(0,0,0,1)
jel to krivo rješenje ili ?? ne kužim
| .anchy. (napisa): | @Megy Poe: pa vidiš da je u tablicama 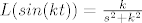
Znači,tebi fali k u brojniku,pa jednostavno pomnožiš sa 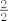 , i dvojku staviš u brojnik,a , i dvojku staviš u brojnik,a 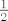 izlučiš ispred Laplace-a i dobiješ izlučiš ispred Laplace-a i dobiješ 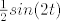
edit:može netko objasniti postupak kako dobimo Jordnaovu bazu kod matrica kojima je npr dimenzija svojstvenog potprostora 2,a geometrijska kratnost sv.vrijednosti 3?
Primjer iz vježbi,
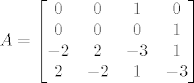
karakteristični polinom je 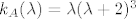
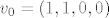
Dobili smo da je baza svoj.potprostora za -2 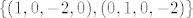 . .
Sada mi nije dalje jasno kako smo dobili 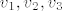  |
Ja sam baš htjela postaviti pitanje za taj primjer matrice.
ja sam to išla računat preko :
Av1=0
Av2=-2v2+v3
Av3=-2v3
Av4=-2v4
i iz toga dobim da je su mi sv vektori = (1,1,0,0),(1,0,-2,0),(0,1,0,-2),(0,0,0,1)
jel to krivo rješenje ili ?? ne kužim
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
Megy Poe
Forumaš(ica)

Pridružen/a: 05. 11. 2009. (23:14:52)
Postovi: (122)16
|
|
| [Vrh] |
|
sasha.f
Forumaš(ica)

Pridružen/a: 25. 10. 2011. (20:04:19)
Postovi: (3D)16
|
|
| [Vrh] |
|
banank0
Forumaš(ica)
Pridružen/a: 11. 06. 2013. (13:36:04)
Postovi: (25)16
|
|
| [Vrh] |
|
ipeula
Forumaš(ica)

Pridružen/a: 07. 01. 2013. (20:24:46)
Postovi: (3)16
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
student_92
Forumaš(ica)

Pridružen/a: 17. 09. 2011. (16:31:46)
Postovi: (B9)16
|
 Postano: 18:29 sub, 1. 2. 2014 Naslov: Postano: 18:29 sub, 1. 2. 2014 Naslov: |
    |
|
|
Pitanje: Ako želim primijeniti formulu [tex]f(x) = e^{\alpha x} (P_m (x) \cos (\beta x) + Q_n (x) \sin (\beta x))[/tex] na [tex]f(x) = 18x e^{-x}[/tex], onda stavim [tex]\alpha = -1, \beta = 0, P_m (x) = 18x, m = 1[/tex]. Sada mogu staviti [tex]n = -1[/tex] ako uzmem da je [tex]Q_n[/tex] nulpolinom pa mi je onda [tex]l = 1[/tex] (maksimum od m i n). Ali zbog [tex]\beta = 0[/tex] svejedno mi je kakav je [tex]Q_n[/tex] jer je svakako [tex]Q_n \cdot \sin (0 \cdot x) = 0[/tex]. [b]Konačno, pitanje je[/b]: je li dobro u ovakvoj situaciji uzeti [tex]n \leq m[/tex] pa da mi onda ispadne [tex]l = m[/tex]? Rješenje ovoga zadatka ispalo mi je dobro tim postupkom.
Pitanje: Ako želim primijeniti formulu [tex]f(x) = e^{\alpha x} (P_m (x) \cos (\beta x) + Q_n (x) \sin (\beta x))[/tex] na [tex]f(x) = 18x e^{-x}[/tex], onda stavim [tex]\alpha = -1, \beta = 0, P_m (x) = 18x, m = 1[/tex]. Sada mogu staviti [tex]n = -1[/tex] ako uzmem da je [tex]Q_n[/tex] nulpolinom pa mi je onda [tex]l = 1[/tex] (maksimum od m i n). Ali zbog [tex]\beta = 0[/tex] svejedno mi je kakav je [tex]Q_n[/tex] jer je svakako [tex]Q_n \cdot \sin (0 \cdot x) = 0[/tex]. Konačno, pitanje je: je li dobro u ovakvoj situaciji uzeti [tex]n \leq m[/tex] pa da mi onda ispadne [tex]l = m[/tex]? Rješenje ovoga zadatka ispalo mi je dobro tim postupkom.
|
|
| [Vrh] |
|
banank0
Forumaš(ica)
Pridružen/a: 11. 06. 2013. (13:36:04)
Postovi: (25)16
|
 Postano: 19:30 sub, 1. 2. 2014 Naslov: Postano: 19:30 sub, 1. 2. 2014 Naslov: |
    |
|
|
[quote="student_92"]Pitanje: Ako želim primijeniti formulu [tex]f(x) = e^{\alpha x} (P_m (x) \cos (\beta x) + Q_n (x) \sin (\beta x))[/tex] na [tex]f(x) = 18x e^{-x}[/tex], onda stavim [tex]\alpha = -1, \beta = 0, P_m (x) = 18x, m = 1[/tex]. Sada mogu staviti [tex]n = -1[/tex] ako uzmem da je [tex]Q_n[/tex] nulpolinom pa mi je onda [tex]l = 1[/tex] (maksimum od m i n). Ali zbog [tex]\beta = 0[/tex] svejedno mi je kakav je [tex]Q_n[/tex] jer je svakako [tex]Q_n \cdot \sin (0 \cdot x) = 0[/tex]. [b]Konačno, pitanje je[/b]: je li dobro u ovakvoj situaciji uzeti [tex]n \leq m[/tex] pa da mi onda ispadne [tex]l = m[/tex]? Rješenje ovoga zadatka ispalo mi je dobro tim postupkom.[/quote]
Da.
| student_92 (napisa): | | Pitanje: Ako želim primijeniti formulu [tex]f(x) = e^{\alpha x} (P_m (x) \cos (\beta x) + Q_n (x) \sin (\beta x))[/tex] na [tex]f(x) = 18x e^{-x}[/tex], onda stavim [tex]\alpha = -1, \beta = 0, P_m (x) = 18x, m = 1[/tex]. Sada mogu staviti [tex]n = -1[/tex] ako uzmem da je [tex]Q_n[/tex] nulpolinom pa mi je onda [tex]l = 1[/tex] (maksimum od m i n). Ali zbog [tex]\beta = 0[/tex] svejedno mi je kakav je [tex]Q_n[/tex] jer je svakako [tex]Q_n \cdot \sin (0 \cdot x) = 0[/tex]. Konačno, pitanje je: je li dobro u ovakvoj situaciji uzeti [tex]n \leq m[/tex] pa da mi onda ispadne [tex]l = m[/tex]? Rješenje ovoga zadatka ispalo mi je dobro tim postupkom. |
Da.
|
|
| [Vrh] |
|
slonic~tonic
Forumaš(ica)

Pridružen/a: 26. 10. 2011. (14:16:34)
Postovi: (84)16
Spol: 
|
|
| [Vrh] |
|
aptx
Forumaš(ica)

Pridružen/a: 11. 01. 2013. (00:15:01)
Postovi: (15)16
|
|
| [Vrh] |
|
banank0
Forumaš(ica)
Pridružen/a: 11. 06. 2013. (13:36:04)
Postovi: (25)16
|
|
| [Vrh] |
|
slonic~tonic
Forumaš(ica)

Pridružen/a: 26. 10. 2011. (14:16:34)
Postovi: (84)16
Spol: 
|
|
| [Vrh] |
|
banank0
Forumaš(ica)
Pridružen/a: 11. 06. 2013. (13:36:04)
Postovi: (25)16
|
|
| [Vrh] |
|
aptx
Forumaš(ica)

Pridružen/a: 11. 01. 2013. (00:15:01)
Postovi: (15)16
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
banank0
Forumaš(ica)
Pridružen/a: 11. 06. 2013. (13:36:04)
Postovi: (25)16
|
 Postano: 19:00 ned, 2. 2. 2014 Naslov: Postano: 19:00 ned, 2. 2. 2014 Naslov: |
    |
|
|
[quote="aptx"][quote="banank0"][quote="aptx"]Može kratke upute što se radi sa 3.b) ?
http://web.math.pmf.unizg.hr/nastava/odif/kolokviji/odjkol22011.pdf[/quote]
rješavaš po onoj velikoj formuli za rj nehomogenog sustava. lako je tu kad ti je e^tA već izračunat. staviš W(t)=e^tA jer je to fundametalna matrica i dalje radiš po formuli
[size=9][color=#999999]Added after 2 minutes:[/color][/size]
[/quote]
Dakle, računa se inverz od W(t) ?
Zašto je onda zadana matrica A?[/quote]
po meni, ta matrica A je meni tu viška. i niš ne predstavlja
imamo fundametalno rj e^tA i ne moramo ga računat, samo ubacimo u formule.
[size=9][color=#999999]Added after 1 minutes:[/color][/size]
[quote="Anonymous"]Pitanje vezano za 2. zadatak ispod one tablice partikularnih rjesenja koji smo radili na vjezbama. Dobili smo da su nultocke pripadne homogene jednadzbe 2i i -2i i sad kak dobijemo da je cos(4i)=0 i zasto smo kod tog drugog dijela (-(x/2)*cos(2x)) gledali nultocku 2i, sto je s nultockom -2i?[/quote]
gledalui smo jedino da odredimo kratnost. isčitamo da je alfa=0, beta = 2
i gledamo je li alfa + i beta rješenje karak. jednadžbe. dobijemo 2i, i vidimo da je njena kratnost 1 pa je r= 1
| aptx (napisa): | | banank0 (napisa): |
rješavaš po onoj velikoj formuli za rj nehomogenog sustava. lako je tu kad ti je e^tA već izračunat. staviš W(t)=e^tA jer je to fundametalna matrica i dalje radiš po formuli
Added after 2 minutes:
|
Dakle, računa se inverz od W(t) ?
Zašto je onda zadana matrica A? |
po meni, ta matrica A je meni tu viška. i niš ne predstavlja
imamo fundametalno rj e^tA i ne moramo ga računat, samo ubacimo u formule.
Added after 1 minutes:
| Anonymous (napisa): | | Pitanje vezano za 2. zadatak ispod one tablice partikularnih rjesenja koji smo radili na vjezbama. Dobili smo da su nultocke pripadne homogene jednadzbe 2i i -2i i sad kak dobijemo da je cos(4i)=0 i zasto smo kod tog drugog dijela (-(x/2)*cos(2x)) gledali nultocku 2i, sto je s nultockom -2i? |
gledalui smo jedino da odredimo kratnost. isčitamo da je alfa=0, beta = 2
i gledamo je li alfa + i beta rješenje karak. jednadžbe. dobijemo 2i, i vidimo da je njena kratnost 1 pa je r= 1
|
|
| [Vrh] |
|
|






