| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
Tomislav
Forumaš(ica)

Pridružen/a: 04. 10. 2010. (20:18:25)
Postovi: (181)16
Spol: 
|
 Postano: 20:49 čet, 13. 1. 2011 Naslov: Postano: 20:49 čet, 13. 1. 2011 Naslov: |
    |
|
|
Ok neka su a1,a2,...,a5 brojevi takvi da je f(ai)=p, za i=1,..5.
Sada je f(x)-p=g(x)*(x-a1)..(x-a5)
Neka je y nultocka od f.
Sad je -p=(y-a1)...(y-a5)g(y)
Znaci da bi -p imao najmanje 5 razlicitih djelitelja,a ima ih samo 4, tj. +-1, +-p.
:)
Ok neka su a1,a2,...,a5 brojevi takvi da je f(ai)=p, za i=1,..5.
Sada je f(x)-p=g(x)*(x-a1)..(x-a5)
Neka je y nultocka od f.
Sad je -p=(y-a1)...(y-a5)g(y)
Znaci da bi -p imao najmanje 5 razlicitih djelitelja,a ima ih samo 4, tj. +-1, +-p.

|
|
| [Vrh] |
|
Lepi91
Forumaš(ica)


Pridružen/a: 15. 09. 2010. (15:22:23)
Postovi: (C8)16
Spol: 
|
|
| [Vrh] |
|
pupi
Forumaš(ica)

Pridružen/a: 20. 12. 2009. (11:03:15)
Postovi: (92)16
Spol: 
|
|
| [Vrh] |
|
pupi
Forumaš(ica)

Pridružen/a: 20. 12. 2009. (11:03:15)
Postovi: (92)16
Spol: 
|
|
| [Vrh] |
|
satja
Forumaš(ica)

Pridružen/a: 16. 05. 2010. (10:44:17)
Postovi: (F1)16
|
|
| [Vrh] |
|
Neno
Forumaš(ica)

Pridružen/a: 08. 02. 2008. (20:03:15)
Postovi: (98)16
Spol: 
Lokacija: Zagreb
|
|
| [Vrh] |
|
jema
Forumaš(ica)

Pridružen/a: 29. 09. 2011. (15:56:35)
Postovi: (52)16
|
 Postano: 22:08 pet, 6. 1. 2012 Naslov: Postano: 22:08 pet, 6. 1. 2012 Naslov: |
    |
|
|
moze par pitanja za 5. zadacu...3. zadatak radili smo na vjezbama skoro isti,, znaci da (x-alfa)|M(p,p')...i sad ja krenem radit tu mjeru od p,p' no nikako da dobijem na kraju 0. dobijem ovako: prvo dijeljenje mi daje ostatak x^2+x+1, drugo mi daje ostatak 2x+1 i onda kad podijelim x^2+x+1 sa 2x+1 dobijem ostatak 3/4....?? za 4.zad., je li odg ne? i jos...kako da otvorim rar ako ne mogu stisnut ono use evoluation version? XD ili ako je netko to skinuo, ako moze da mi to upload-a tu, ako se to moze XD hvala :)
moze par pitanja za 5. zadacu...3. zadatak radili smo na vjezbama skoro isti,, znaci da (x-alfa)|M(p,p')...i sad ja krenem radit tu mjeru od p,p' no nikako da dobijem na kraju 0. dobijem ovako: prvo dijeljenje mi daje ostatak x^2+x+1, drugo mi daje ostatak 2x+1 i onda kad podijelim x^2+x+1 sa 2x+1 dobijem ostatak 3/4....?? za 4.zad., je li odg ne? i jos...kako da otvorim rar ako ne mogu stisnut ono use evoluation version? XD ili ako je netko to skinuo, ako moze da mi to upload-a tu, ako se to moze XD hvala 
|
|
| [Vrh] |
|
Zenon
Forumaš(ica)


Pridružen/a: 09. 09. 2011. (19:14:43)
Postovi: (2B1)16
Sarma: -
Lokacija: [tex]\pm\infty[/tex]
|
 Postano: 23:04 pon, 9. 1. 2012 Naslov: Postano: 23:04 pon, 9. 1. 2012 Naslov: |
    |
|
|
Hello!
Molim pomoć oko zadatka iz zadaće :)
Odredi sve [tex]a,b\in\mathbb R[/tex] takve da polinom [tex]p(x)=x^4-4x^3+10x^2+ax+b[/tex] ima dvije dvostruke nultočke.
Probao sam napisati [tex]p(x)=\left(x+A\right)^2\left(x+B\right)^2=\left[\left(x+A\right)\left(x+B\right)\right]^2=\left(x^2+(A+B)x+AB\right)^2=x^4+2(A+B)x^3+\left((A+B)^2+2AB\right)x^2+2(A+B)ABx+A^2B^2[/tex], raspisati, izjednačiti koeficijente i dobijem:
[dtex]\left.\begin{array}{lcr}A+B&=&-2\\\left(A+B\right)^2+2AB&=&10\\2AB\left(A+B\right)&=&a\\A^2B^2&=&b\end{array}\right\}[/dtex]
Ups, sad sam ipak uspio dobiti rješenje [tex]A_{1,2}=1\pm3, \ B_{1,2}=-3\pm3[/tex].
I znači to sada samo uvrstim u zadnje dvije jednadžbe sustava i dobijem [tex]a_{1,2} \ i \ b_{1,2}[/tex] i to su onda sigurno sva i jedina rješenja koja zadovoljavaju uvjete zadatka?
Ovo jednostavno moram staviti jer je preškica :D
:krcko: hihihihihihi
Hvala unaprijed! :thankyou:
Hello!
Molim pomoć oko zadatka iz zadaće 
Odredi sve [tex]a,b\in\mathbb R[/tex] takve da polinom [tex]p(x)=x^4-4x^3+10x^2+ax+b[/tex] ima dvije dvostruke nultočke.
Probao sam napisati [tex]p(x)=\left(x+A\right)^2\left(x+B\right)^2=\left[\left(x+A\right)\left(x+B\right)\right]^2=\left(x^2+(A+B)x+AB\right)^2=x^4+2(A+B)x^3+\left((A+B)^2+2AB\right)x^2+2(A+B)ABx+A^2B^2[/tex], raspisati, izjednačiti koeficijente i dobijem:
[dtex]\left.\begin{array}{lcr}A+B&=&-2\\\left(A+B\right)^2+2AB&=&10\\2AB\left(A+B\right)&=&a\\A^2B^2&=&b\end{array}\right\}[/dtex]
Ups, sad sam ipak uspio dobiti rješenje [tex]A_{1,2}=1\pm3, \ B_{1,2}=-3\pm3[/tex].
I znači to sada samo uvrstim u zadnje dvije jednadžbe sustava i dobijem [tex]a_{1,2} \ i \ b_{1,2}[/tex] i to su onda sigurno sva i jedina rješenja koja zadovoljavaju uvjete zadatka?
Ovo jednostavno moram staviti jer je preškica 
 hihihihihihi hihihihihihi
Hvala unaprijed! 
|
|
| [Vrh] |
|
krcko
Forumaš nagrađen za životno djelo


Pridružen/a: 07. 10. 2002. (15:57:59)
Postovi: (18B3)16
|
 Postano: 14:41 uto, 10. 1. 2012 Naslov: Postano: 14:41 uto, 10. 1. 2012 Naslov: |
    |
|
|
Sustav ti je dobar, ali rjesenje mi ispada drugacije ([latex]A,B=1\pm i \sqrt{2}, a=-12, b=9[/latex]). Drugi nacin je preko Euklidovog algoritma: podijelis p s p', onda p' s ostatkom i izjednacis koeficijente novog ostatka s nulom. Dobit ces sustav od dvije jednadzbe u nepoznanicama a, b.
@jema: u prvom dijeljenju ostatak je x^2+x+2, u drugom je nula. U cetvrtom zadatku odgovor je ne, a ti objasni zasto :) I nemoj vise cross postati! :x
Sustav ti je dobar, ali rjesenje mi ispada drugacije (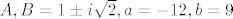 ). Drugi nacin je preko Euklidovog algoritma: podijelis p s p', onda p' s ostatkom i izjednacis koeficijente novog ostatka s nulom. Dobit ces sustav od dvije jednadzbe u nepoznanicama a, b. ). Drugi nacin je preko Euklidovog algoritma: podijelis p s p', onda p' s ostatkom i izjednacis koeficijente novog ostatka s nulom. Dobit ces sustav od dvije jednadzbe u nepoznanicama a, b.
@jema: u prvom dijeljenju ostatak je x^2+x+2, u drugom je nula. U cetvrtom zadatku odgovor je ne, a ti objasni zasto  I nemoj vise cross postati! I nemoj vise cross postati! 
_________________
Vedran Krcadinac
Ljudi su razliciti, a nula je paran broj.
Zadnja promjena: krcko; 14:52 uto, 10. 1. 2012; ukupno mijenjano 1 put.
|
|
| [Vrh] |
|
vsego
Site Admin


Pridružen/a: 06. 10. 2002. (22:07:09)
Postovi: (3562)16
Spol: 
Lokacija: /sbin/init
|
|
| [Vrh] |
|
Zenon
Forumaš(ica)


Pridružen/a: 09. 09. 2011. (19:14:43)
Postovi: (2B1)16
Sarma: -
Lokacija: [tex]\pm\infty[/tex]
|
|
| [Vrh] |
|
dalmatinčica
Forumaš(ica)


Pridružen/a: 01. 10. 2011. (18:46:54)
Postovi: (AC)16
|
|
| [Vrh] |
|
jema
Forumaš(ica)

Pridružen/a: 29. 09. 2011. (15:56:35)
Postovi: (52)16
|
|
| [Vrh] |
|
Zenon
Forumaš(ica)


Pridružen/a: 09. 09. 2011. (19:14:43)
Postovi: (2B1)16
Sarma: -
Lokacija: [tex]\pm\infty[/tex]
|
|
| [Vrh] |
|
gflegar
Forumaš(ica)


Pridružen/a: 12. 10. 2011. (15:03:41)
Postovi: (10D)16
Spol: 
|
|
| [Vrh] |
|
zaruljica
Forumaš(ica)

Pridružen/a: 23. 09. 2011. (13:15:25)
Postovi: (41)16
Spol: 
Lokacija: Split/Zagreb
|
|
| [Vrh] |
|
gflegar
Forumaš(ica)


Pridružen/a: 12. 10. 2011. (15:03:41)
Postovi: (10D)16
Spol: 
|
 Postano: 18:11 uto, 10. 1. 2012 Naslov: Postano: 18:11 uto, 10. 1. 2012 Naslov: |
    |
|
|
5. zadatak iz 5. zadace:
Sa [tex]x_1, x_2, \ldots, x_5[/tex] oznacimo tocke u kojima polinom [tex]f[/tex] poprima vrijednost [tex]p[/tex]. U tim tockama polinom [tex] F(x) = f(x) - p[/tex] poprima [tex]0[/tex] pa su [tex]x_1, x_2, \ldots, x_5[/tex] nultocke polinoma [tex]F[/tex], tj.
[dtex]F(x) = (x - x_1) \ldots (x-x_5)q(x) \Rightarrow f(x) = (x - x_1) \ldots (x-x_5)q(x) + p[/dtex]
Pretpostavimo da polinom [tex]f[/tex] ima cjelobrojnu nultocku [tex]x_0[/tex].
Tada vrijedi:
[dtex] f(x_0) = (x_0 - x_1) \ldots (x_0 - x_5)q(x_0) + p = 0 \Rightarrow (x_0 - x_1) \ldots (x_0 - x_5)q(x_0) = -p[/dtex]
Kako su [tex]x_1, \ldots, x_5[/tex] medjusobno razliciti, [tex]x_0-x_1, \ldots x_0-x_5[/tex] su medjusobno razliciti djelitelji broja [tex]-p[/tex].
Ali to je kontradikcija jer je [tex]p[/tex] prost pa su mu jednini djelitelji [tex]1, -1, p, -p[/tex].
Dakle, [tex]f[/tex] nema cjelobrojnih nultocaka.
5. zadatak iz 5. zadace:
Sa [tex]x_1, x_2, \ldots, x_5[/tex] oznacimo tocke u kojima polinom [tex]f[/tex] poprima vrijednost [tex]p[/tex]. U tim tockama polinom [tex] F(x) = f(x) - p[/tex] poprima [tex]0[/tex] pa su [tex]x_1, x_2, \ldots, x_5[/tex] nultocke polinoma [tex]F[/tex], tj.
[dtex]F(x) = (x - x_1) \ldots (x-x_5)q(x) \Rightarrow f(x) = (x - x_1) \ldots (x-x_5)q(x) + p[/dtex]
Pretpostavimo da polinom [tex]f[/tex] ima cjelobrojnu nultocku [tex]x_0[/tex].
Tada vrijedi:
[dtex] f(x_0) = (x_0 - x_1) \ldots (x_0 - x_5)q(x_0) + p = 0 \Rightarrow (x_0 - x_1) \ldots (x_0 - x_5)q(x_0) = -p[/dtex]
Kako su [tex]x_1, \ldots, x_5[/tex] medjusobno razliciti, [tex]x_0-x_1, \ldots x_0-x_5[/tex] su medjusobno razliciti djelitelji broja [tex]-p[/tex].
Ali to je kontradikcija jer je [tex]p[/tex] prost pa su mu jednini djelitelji [tex]1, -1, p, -p[/tex].
Dakle, [tex]f[/tex] nema cjelobrojnih nultocaka.
|
|
| [Vrh] |
|
zaruljica
Forumaš(ica)


Pridružen/a: 23. 09. 2011. (13:15:25)
Postovi: (41)16
Spol: 
Lokacija: Split/Zagreb
|
|
| [Vrh] |
|
krcko
Forumaš nagrađen za životno djelo


Pridružen/a: 07. 10. 2002. (15:57:59)
Postovi: (18B3)16
|
|
| [Vrh] |
|
Zenon
Forumaš(ica)


Pridružen/a: 09. 09. 2011. (19:14:43)
Postovi: (2B1)16
Sarma: -
Lokacija: [tex]\pm\infty[/tex]
|
|
| [Vrh] |
|
|














