| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
smajl
Forumaš(ica)

Pridružen/a: 02. 01. 2010. (12:59:23)
Postovi: (EB)16
Spol: 
Lokacija: Zagreb
|
|
| [Vrh] |
|
kkarlo
Forumaš(ica)

Pridružen/a: 19. 05. 2010. (08:43:59)
Postovi: (1B2)16
Spol: 
|
|
| [Vrh] |
|
smajl
Forumaš(ica)

Pridružen/a: 02. 01. 2010. (12:59:23)
Postovi: (EB)16
Spol: 
Lokacija: Zagreb
|
|
| [Vrh] |
|
Swerz
Forumaš(ica)


Pridružen/a: 13. 02. 2009. (21:30:28)
Postovi: (182)16
Spol: 
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
pravipurger
Forumaš(ica)


Pridružen/a: 11. 07. 2009. (10:29:44)
Postovi: (128)16
Spol: 
|
 Postano: 16:47 sub, 14. 1. 2012 Naslov: Postano: 16:47 sub, 14. 1. 2012 Naslov: |
    |
|
|
[quote="Anonymous"]Može li mi netko pomoć oko 6.zad ovdje http://web.math.pmf.unizg.hr/nastava/vekt/files/2009-10/popravak_2kol_0910.pdf
hvala[/quote]
A je hermitski ako i samo ako je normalan i spektar mu je podskup od R. Spektar ovog operatora o(f(H))=f(o(H))=0, dakle o(H)={1,-1,0} (o mi je oznaka za spektar, 1,-1,0 sam dobio kao nultočke polinoma x^4-x^3-x^2+x)
Dakle spektar je podskup od R -> op je hermitski.
(mislim da je tako)
A je hermitski ako i samo ako je normalan i spektar mu je podskup od R. Spektar ovog operatora o(f(H))=f(o(H))=0, dakle o(H)={1,-1,0} (o mi je oznaka za spektar, 1,-1,0 sam dobio kao nultočke polinoma x^4-x^3-x^2+x)
Dakle spektar je podskup od R → op je hermitski.
(mislim da je tako)
_________________
No, you clearly don’t know who you’re talking to, so let me clue you in: I am not in danger, Skylar. I am the danger. A guy opens his door and gets shot and you think that of me? No. I am the one who knocks.
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
pajopatak
Forumaš(ica)

Pridružen/a: 25. 10. 2009. (22:20:04)
Postovi: (BE)16
|
|
| [Vrh] |
|
Anon
Forumaš(ica)

Pridružen/a: 30. 01. 2011. (20:08:14)
Postovi: (3)16
Lokacija: Zagreb
|
|
| [Vrh] |
|
Flame
Forumaš(ica)

Pridružen/a: 12. 08. 2009. (02:14:39)
Postovi: (53)16
Spol: 
|
 Postano: 7:39 pon, 16. 1. 2012 Naslov: Postano: 7:39 pon, 16. 1. 2012 Naslov: |
    |
|
|
To je apsolutno tocno, i lako se pokaze da je to upravo ortogonalna projekcija na zadani potprostor (sto je sasvim ocekivano, primjerice uzmi tocku T i pravac u ravnini... od svih tocaka pravca, od T je najmanje udaljeno sjeciste pravca i okomice na pravac kroz T).
Ortogonalna projekcija vektora [latex]x[/latex] na potprostor [latex]W[/latex] je zadana formulom [latex]\displaystyle\sum_{i=1}^k \langle x, e_i \rangle e_i[/latex] gdje je [latex]\{e_1,...,e_k\}[/latex] ortonormirana baza za [latex]W[/latex].
A nije bas da nigdje nema formule ni postupka, to se radilo jos na linearnoj 2 i na vjezbama i predavanjima, a vjerujem da se radilo i na ovom kolegiju, iako ne mogu garantirati jer nisam dolazio. Evo, pogledao sam i u skripti profesora Muica i profesora Primca (online), u sadrzaju stoji: 7.8. Teorem o projekciji i najbolja aproksimacija. Pretpostavljam da je obradjeno :)
To je apsolutno tocno, i lako se pokaze da je to upravo ortogonalna projekcija na zadani potprostor (sto je sasvim ocekivano, primjerice uzmi tocku T i pravac u ravnini... od svih tocaka pravca, od T je najmanje udaljeno sjeciste pravca i okomice na pravac kroz T).
Ortogonalna projekcija vektora  na potprostor na potprostor 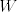 je zadana formulom je zadana formulom 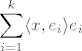 gdje je gdje je 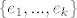 ortonormirana baza za ortonormirana baza za 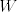 . .
A nije bas da nigdje nema formule ni postupka, to se radilo jos na linearnoj 2 i na vjezbama i predavanjima, a vjerujem da se radilo i na ovom kolegiju, iako ne mogu garantirati jer nisam dolazio. Evo, pogledao sam i u skripti profesora Muica i profesora Primca (online), u sadrzaju stoji: 7.8. Teorem o projekciji i najbolja aproksimacija. Pretpostavljam da je obradjeno 
|
|
| [Vrh] |
|
Lepi91
Forumaš(ica)


Pridružen/a: 15. 09. 2010. (15:22:23)
Postovi: (C8)16
Spol: 
|
 Postano: 8:52 pon, 16. 1. 2012 Naslov: Postano: 8:52 pon, 16. 1. 2012 Naslov: |
    |
|
|
imas matricu A u M2(2*2 matrica) i neki zdani potprostor M=[{A1,A2,A3}] matrice M2
prvo provijeris da su A1,2,A3 nezavisne,ok...sad ortonornormiramo A1,A2,A3
...gram-schmitd...i dobijes E1,E2,E3 i onda najbolja aproksimacija matrice A ti je matrica B koja izgleda B=<A|E1>E1 + <A|E2>E2 + <A|E3>E3
gdje ti je <|> skalarni produkt
nadam se da ce pomoc...
i sad naravno varijacije na to,vece matrice ili umjesto matrice polinomi i tako...
imas matricu A u M2(2*2 matrica) i neki zdani potprostor M=[{A1,A2,A3}] matrice M2
prvo provijeris da su A1,2,A3 nezavisne,ok...sad ortonornormiramo A1,A2,A3
...gram-schmitd...i dobijes E1,E2,E3 i onda najbolja aproksimacija matrice A ti je matrica B koja izgleda B=<A|E1>E1 + <A|E2>E2 + <A|E3>E3
gdje ti je <|> skalarni produkt
nadam se da ce pomoc...
i sad naravno varijacije na to,vece matrice ili umjesto matrice polinomi i tako...
_________________
tko rano rani,malo spava
|
|
| [Vrh] |
|
gogo_
Forumaš(ica)

Pridružen/a: 07. 10. 2009. (17:06:47)
Postovi: (3F)16
|
|
| [Vrh] |
|
spot137
Forumaš(ica)
Pridružen/a: 02. 11. 2009. (13:33:18)
Postovi: (55)16
Spol: 
|
|
| [Vrh] |
|
dine
Forumaš(ica)

Pridružen/a: 21. 06. 2010. (16:06:19)
Postovi: (18)16
Spol: 
Lokacija: dark side of the moon
|
 Postano: 3:22 sub, 28. 1. 2012 Naslov: Postano: 3:22 sub, 28. 1. 2012 Naslov: |
    |
|
|
[quote="pravipurger"][quote="Anonymous"]Može li mi netko pomoć oko 6.zad ovdje http://web.math.pmf.unizg.hr/nastava/vekt/files/2009-10/popravak_2kol_0910.pdf
hvala[/quote]
A je hermitski [b]ako i samo ako[/b] je normalan i spektar mu je podskup od R. Spektar ovog operatora o(f(H))=f(o(H))=0, dakle o(H)={1,-1,0} (o mi je oznaka za spektar, 1,-1,0 sam dobio kao nultočke polinoma x^4-x^3-x^2+x)
Dakle spektar je podskup od R -> op je hermitski.
(mislim da je tako)[/quote]
očito vrijedi ako je hermitski da je onda normalan, no nisam siguran za obrat, barem nisam uspio naći teorem koji to kaže, a ne znam kako bi dokazao
[size=9][color=#999999]Added after 11 minutes:[/color][/size]
[quote="spot137"]Jel zna tko riješiti 5,6 i 7 zadatak ovgodisnjeg kolokvija?
http://web.math.pmf.unizg.hr/nastava/vekt/files/2011-12/2_kol_11_12.pdf[/quote]
6.zad f(H)= H^3333 + H^333 + H^33 + H^3 - 4I =0 znaš da je jedna nultočka I, kad deriviraš funkciju dobije se da je derivacija konstantnog predzaka (zbog parnih potencija) pa je funkcija monotona pa ima samo jednu nultočku i onda je nužno H=I
| pravipurger (napisa): |
A je hermitski ako i samo ako je normalan i spektar mu je podskup od R. Spektar ovog operatora o(f(H))=f(o(H))=0, dakle o(H)={1,-1,0} (o mi je oznaka za spektar, 1,-1,0 sam dobio kao nultočke polinoma x^4-x^3-x^2+x)
Dakle spektar je podskup od R → op je hermitski.
(mislim da je tako) |
očito vrijedi ako je hermitski da je onda normalan, no nisam siguran za obrat, barem nisam uspio naći teorem koji to kaže, a ne znam kako bi dokazao
Added after 11 minutes:
6.zad f(H)= H^3333 + H^333 + H^33 + H^3 - 4I =0 znaš da je jedna nultočka I, kad deriviraš funkciju dobije se da je derivacija konstantnog predzaka (zbog parnih potencija) pa je funkcija monotona pa ima samo jednu nultočku i onda je nužno H=I
_________________
The death is road to awe
|
|
| [Vrh] |
|
slonic~tonic
Forumaš(ica)

Pridružen/a: 26. 10. 2011. (14:16:34)
Postovi: (84)16
Spol: 
|
|
| [Vrh] |
|
kkarlo
Forumaš(ica)

Pridružen/a: 19. 05. 2010. (08:43:59)
Postovi: (1B2)16
Spol: 
|
|
| [Vrh] |
|
jackass9
Forumaš(ica)

Pridružen/a: 19. 09. 2009. (10:23:58)
Postovi: (15D)16
Spol: 
Lokacija: pod stolom
|
|
| [Vrh] |
|
kkarlo
Forumaš(ica)

Pridružen/a: 19. 05. 2010. (08:43:59)
Postovi: (1B2)16
Spol: 
|
|
| [Vrh] |
|
jackass9
Forumaš(ica)

Pridružen/a: 19. 09. 2009. (10:23:58)
Postovi: (15D)16
Spol: 
Lokacija: pod stolom
|
|
| [Vrh] |
|
|


















