| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
kkarlo
Forumaš(ica)

Pridružen/a: 19. 05. 2010. (08:43:59)
Postovi: (1B2)16
Spol: 
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
spot137
Forumaš(ica)
Pridružen/a: 02. 11. 2009. (13:33:18)
Postovi: (55)16
Spol: 
|
|
| [Vrh] |
|
jackass9
Forumaš(ica)

Pridružen/a: 19. 09. 2009. (10:23:58)
Postovi: (15D)16
Spol: 
Lokacija: pod stolom
|
 Postano: 13:04 sub, 28. 1. 2012 Naslov: Postano: 13:04 sub, 28. 1. 2012 Naslov: |
    |
|
|
@kkarlo:
ma ja sam išao rješavati, rekoh ne škodi ako nešto napišem pa možda koji bod pokupim :)
@Gost:
to ja nemam u vježbama. A imam sve što se spominjalo...vjerojatno si ti kod drugog asistenta(ja sam kod Ane)
[size=9][color=#999999]Added after 6 minutes:[/color][/size]
[quote="spot137"]pa ja sam tako krenula (mislim na 5. zad), nisam stigla do kraja i dobila sam 0 :(
mozes napisati kako tocno ide?
a je li itko zna zadnji?
kad smo mi uopce radili tu polarnu formu?[/quote]
u našoj grupi je teorem o njoj spomenut kod pozitivnih operatora
A zadnji zadatak znam dokazat jedan smjer sigurno, a za drugi nisam sto posto siguran pa neću ni pisat
Dakle, U je unitarni operator, P je pozitivni (hermitski)
[u]Smjer gdje se treba dokazati da je A normalan(<=)[/u]
A=PU
A*=(PU)*=U*P*
AA*=PUU*P*=PIP*(jer je U unitaran)=PP*=PP(jer je P hermitski)
A*A=U*P*PU=U*PPU(jer je P hermitski)=U*PUP(komutativnost dana u uvjetu)=U*UPP(opet komutativnost)=IPP(U unitaran)=PP
i iz toga se vidi da je A normalan
@kkarlo:
ma ja sam išao rješavati, rekoh ne škodi ako nešto napišem pa možda koji bod pokupim 
@Gost:
to ja nemam u vježbama. A imam sve što se spominjalo...vjerojatno si ti kod drugog asistenta(ja sam kod Ane)
Added after 6 minutes:
| spot137 (napisa): | pa ja sam tako krenula (mislim na 5. zad), nisam stigla do kraja i dobila sam 0 
mozes napisati kako tocno ide?
a je li itko zna zadnji?
kad smo mi uopce radili tu polarnu formu? |
u našoj grupi je teorem o njoj spomenut kod pozitivnih operatora
A zadnji zadatak znam dokazat jedan smjer sigurno, a za drugi nisam sto posto siguran pa neću ni pisat
Dakle, U je unitarni operator, P je pozitivni (hermitski)
Smjer gdje se treba dokazati da je A normalan(⇐)
A=PU
A*=(PU)*=U*P*
AA*=PUU*P*=PIP*(jer je U unitaran)=PP*=PP(jer je P hermitski)
A*A=U*P*PU=U*PPU(jer je P hermitski)=U*PUP(komutativnost dana u uvjetu)=U*UPP(opet komutativnost)=IPP(U unitaran)=PP
i iz toga se vidi da je A normalan
_________________
Nema mozga do malog mozga
|
|
| [Vrh] |
|
.anchy.
Forumaš(ica)

Pridružen/a: 14. 11. 2007. (20:03:46)
Postovi: (1BC)16
Lokacija: Zgb
|
 Postano: 13:50 sub, 28. 1. 2012 Naslov: Postano: 13:50 sub, 28. 1. 2012 Naslov: |
    |
|
|
[quote="jackass9"]
@Gost:
to ja nemam u vježbama. A imam sve što se spominjalo...vjerojatno si ti kod drugog asistenta(ja sam kod Ane) [/quote]
A kako onda ja imam? Isto sam kod Ane, minimalno 3 zadatka u kojima se spominje: prvi tamo gdje smo dokazali da je spektar hermitskog podskup relanih brojeva,pa smo dokazali što je spektar ntihermitskog i unitarnog, koristi se ta činjenica u zad 4.4.3 i u predzadnjem zadatku koji smo riješili(koliko najviše elta ima spektar unitarnog operatora...)
[quote="jackass9"]
A zadnji zadatak znam dokazat jedan smjer sigurno, a za drugi nisam sto posto siguran pa neću ni pisat
Dakle, U je unitarni operator, P je pozitivni (hermitski)
[u]Smjer gdje se treba dokazati da je A normalan(<=)[/u]
A=PU
A*=(PU)*=U*P*
AA*=PUU*P*=PIP*(jer je U unitaran)=PP*=PP(jer je P hermitski)
A*A=U*P*PU=U*PPU(jer je P hermitski)=U*PUP(komutativnost dana u uvjetu)=U*UPP(opet komutativnost)=IPP(U unitaran)=PP
i iz toga se vidi da je A normalan[/quote]
=> smjer:
Neka je A normalan,tj AA*=A*A.
AA*=PU(PU)*=PUU*P*
A*A=U*P*PU
PUU*P*=U*P*PU (pomnožimo sa desne strane s U)
UPUU*P*=UU*P*PU (U unitaran)
UPP*=P*PU P hermitski
UP^2=P^2U
U komutira s polinomom od P,pa komutira i s P.
| jackass9 (napisa): |
@Gost:
to ja nemam u vježbama. A imam sve što se spominjalo...vjerojatno si ti kod drugog asistenta(ja sam kod Ane) |
A kako onda ja imam? Isto sam kod Ane, minimalno 3 zadatka u kojima se spominje: prvi tamo gdje smo dokazali da je spektar hermitskog podskup relanih brojeva,pa smo dokazali što je spektar ntihermitskog i unitarnog, koristi se ta činjenica u zad 4.4.3 i u predzadnjem zadatku koji smo riješili(koliko najviše elta ima spektar unitarnog operatora...)
| jackass9 (napisa): |
A zadnji zadatak znam dokazat jedan smjer sigurno, a za drugi nisam sto posto siguran pa neću ni pisat
Dakle, U je unitarni operator, P je pozitivni (hermitski)
Smjer gdje se treba dokazati da je A normalan(⇐)
A=PU
A*=(PU)*=U*P*
AA*=PUU*P*=PIP*(jer je U unitaran)=PP*=PP(jer je P hermitski)
A*A=U*P*PU=U*PPU(jer je P hermitski)=U*PUP(komutativnost dana u uvjetu)=U*UPP(opet komutativnost)=IPP(U unitaran)=PP
i iz toga se vidi da je A normalan |
⇒ smjer:
Neka je A normalan,tj AA*=A*A.
AA*=PU(PU)*=PUU*P*
A*A=U*P*PU
PUU*P*=U*P*PU (pomnožimo sa desne strane s U)
UPUU*P*=UU*P*PU (U unitaran)
UPP*=P*PU P hermitski
UP^2=P^2U
U komutira s polinomom od P,pa komutira i s P.
|
|
| [Vrh] |
|
jackass9
Forumaš(ica)

Pridružen/a: 19. 09. 2009. (10:23:58)
Postovi: (15D)16
Spol: 
Lokacija: pod stolom
|
|
| [Vrh] |
|
slonic~tonic
Forumaš(ica)

Pridružen/a: 26. 10. 2011. (14:16:34)
Postovi: (84)16
Spol: 
|
|
| [Vrh] |
|
Serious Sam
Forumaš(ica)


Pridružen/a: 09. 12. 2009. (15:08:32)
Postovi: (5C)16
Spol: 
|
|
| [Vrh] |
|
slonic~tonic
Forumaš(ica)

Pridružen/a: 26. 10. 2011. (14:16:34)
Postovi: (84)16
Spol: 
|
|
| [Vrh] |
|
kkarlo
Forumaš(ica)

Pridružen/a: 19. 05. 2010. (08:43:59)
Postovi: (1B2)16
Spol: 
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
kkarlo
Forumaš(ica)

Pridružen/a: 19. 05. 2010. (08:43:59)
Postovi: (1B2)16
Spol: 
|
 Postano: 0:00 ned, 29. 1. 2012 Naslov: Postano: 0:00 ned, 29. 1. 2012 Naslov: |
    |
|
|
[quote="Anonymous"]http://web.math.pmf.unizg.hr/nastava/vekt/files/2010-11/popravni_kol2_10_11.pdf
jel bi znao netko 5. rijesit ???? pliz[/quote]
Moguće da griješim ali evo mog pokušaja:
Pošto je P strogo pozitivni operator, to znači da ima i dijagonalni prikaz za svojstvenim vrijednostima na dijagonali sad kad bi računali P^3+2P^2+2P+I, zapravo dobiješ za bilo koji redak u toj nekoj matrici x^3+3x^2+2x+1 gdje x predstavlja svojstvenu vrijednost za taj neki redak... A znamo da je pozitivni operator ujedno i hermitski, a za hermitski smo već utvrdili da su mu svojstvene vrijednosti iz R-a, a isto tako znamo da kod unitarnog operatora modul svojstvene vrijednosti je jednak 1.
Znači ovaj x je realan broj zbog toga što je pretpostavka da je P pozitivan, pa imamo slijedeću jednakost:
x^3+3x^2+2x+1=1,
iz čega dobijemo nultočke 0,-2 i -1. I to su nam jedina rješenja, a to je u kontradikciji sa početnom pretpostavkom da je P strogo pozitivan.
Pošto je x sigurno >0 i realan, onda netreba ni provjeravat rješenja za x^3+3x^2+2x+1=i, x^3+3x^2+2x+1=-i te x^3+3x^2+2x+1=-1, ali bi vjerojatno bilo dobro napisat zašto isključujemo te mogućnosti.
Valjda to tak ide...
:roll:
[size=9][color=#999999]Added after 42 minutes:[/color][/size]
[quote="jackass9"][quote=".anchy."]
[b]
A kako onda ja imam?[/b] [/quote]
Ne znam vjerojatno si puno pametnija il pažljivija :D no,no imam i ja te zadatke
[b]Nije se spominjalo u skroz istom kontekstu al dok sam pročitao malo "koncetriranije" što je kolega/ica Gost napisao/la, shvatio sam gdje je poanta[/b][/quote]
Ajde molim te onda malo pojasni da i ja skužim...
Onaj peti...još mi je uvijek zagonetka...
http://web.math.pmf.unizg.hr/nastava/vekt/files/2011-12/2_kol_11_12.pdf
Koja subota...
Ako netko zna i 6 bio bih zahvalan. Ja sam tu dobio samo 2 boda, a rješio sam ga na sličan(rekao bih isti, ali nemogu sa sigurnošću tvrdit da nisam negdje nešt izostavio) način kako smo rješili onaj u zadaći...
Hvala!
| Anonymous (napisa): | http://web.math.pmf.unizg.hr/nastava/vekt/files/2010-11/popravni_kol2_10_11.pdf
jel bi znao netko 5. rijesit ???? pliz |
Moguće da griješim ali evo mog pokušaja:
Pošto je P strogo pozitivni operator, to znači da ima i dijagonalni prikaz za svojstvenim vrijednostima na dijagonali sad kad bi računali P^3+2P^2+2P+I, zapravo dobiješ za bilo koji redak u toj nekoj matrici x^3+3x^2+2x+1 gdje x predstavlja svojstvenu vrijednost za taj neki redak... A znamo da je pozitivni operator ujedno i hermitski, a za hermitski smo već utvrdili da su mu svojstvene vrijednosti iz R-a, a isto tako znamo da kod unitarnog operatora modul svojstvene vrijednosti je jednak 1.
Znači ovaj x je realan broj zbog toga što je pretpostavka da je P pozitivan, pa imamo slijedeću jednakost:
x^3+3x^2+2x+1=1,
iz čega dobijemo nultočke 0,-2 i -1. I to su nam jedina rješenja, a to je u kontradikciji sa početnom pretpostavkom da je P strogo pozitivan.
Pošto je x sigurno >0 i realan, onda netreba ni provjeravat rješenja za x^3+3x^2+2x+1=i, x^3+3x^2+2x+1=-i te x^3+3x^2+2x+1=-1, ali bi vjerojatno bilo dobro napisat zašto isključujemo te mogućnosti.
Valjda to tak ide...

Added after 42 minutes:
| jackass9 (napisa): | | .anchy. (napisa): |
A kako onda ja imam? |
Ne znam vjerojatno si puno pametnija il pažljivija  no,no imam i ja te zadatke no,no imam i ja te zadatke
Nije se spominjalo u skroz istom kontekstu al dok sam pročitao malo "koncetriranije" što je kolega/ica Gost napisao/la, shvatio sam gdje je poanta |
Ajde molim te onda malo pojasni da i ja skužim...
Onaj peti...još mi je uvijek zagonetka...
http://web.math.pmf.unizg.hr/nastava/vekt/files/2011-12/2_kol_11_12.pdf
Koja subota...
Ako netko zna i 6 bio bih zahvalan. Ja sam tu dobio samo 2 boda, a rješio sam ga na sličan(rekao bih isti, ali nemogu sa sigurnošću tvrdit da nisam negdje nešt izostavio) način kako smo rješili onaj u zadaći...
Hvala!
|
|
| [Vrh] |
|
.anchy.
Forumaš(ica)

Pridružen/a: 14. 11. 2007. (20:03:46)
Postovi: (1BC)16
Lokacija: Zgb
|
 Postano: 9:51 ned, 29. 1. 2012 Naslov: Postano: 9:51 ned, 29. 1. 2012 Naslov: |
    |
|
|
Ovaj peti..imam puno sumnji u rješenje,al evo:
Def. [latex]f(\lambda)=(\lambda - 1)^{2012}
g(\lambda)=(\lambda - 2)^{2013}
h(\lambda)=(\lambda-(1+i))^{2014} [/latex]
[latex]
\lambda \in \sigma(f(A))=f(\sigma(A)) => |\lambda| = 1
[/latex]
[latex]
|\lambda -1|^{2012} =1 [/latex]
[latex]
|\lambda-2|^{2013}=1[/latex]
[latex]
|\lambda-(1+i)|^{2014}=1 [/latex]
sad me muči možemo li umjesto 2012. korijena iz jedinice pisati samo 1 i -1,ili trebamo ostaviti 2012.korijen(u kompl.prostoru ih ima puno,zar ne?)?
onda,jel možemo reći da je [latex]|\lambda -1|=-1 [/latex] nemoguće,ako bismo uzimali samo +-jedinicu kao 2012.korijen iz 1?
Pp da se smije,ali nisam sigurna,s kompl.prostorom sam na Oni :oops:
ako se ovo sve može,onda dobijemo [latex]
|\lambda -1|=1 [/latex]
[latex]
|\lambda-2|=1[/latex]
[latex]
|\lambda-(1+i)|=1 [/latex]
tj.prva jednadžba je kružnica sa središtem u 1 sa radijusom 1,druga jednadžba je kružnica sa središtem u 2 sa radijusom 1,treća jednadžba je kružnica sa središtem u (1,i) - y-os je kompleksna, pa je to zapravo (1,1) - s radijusom 1.
Kada sve tri nacrtamo,vidimo da se te tri kružnice ne sijeku ni u jednoj zajedničkoj točki,pa takav operator ne postoji.
Bilo bi super kad bi mi netko riješio ove nedoumice,i rekao je li ovo točno?
Ovaj peti..imam puno sumnji u rješenje,al evo:
Def. 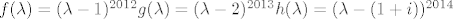
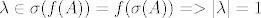
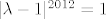
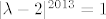
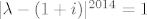
sad me muči možemo li umjesto 2012. korijena iz jedinice pisati samo 1 i -1,ili trebamo ostaviti 2012.korijen(u kompl.prostoru ih ima puno,zar ne?)?
onda,jel možemo reći da je 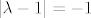 nemoguće,ako bismo uzimali samo +-jedinicu kao 2012.korijen iz 1? nemoguće,ako bismo uzimali samo +-jedinicu kao 2012.korijen iz 1?
Pp da se smije,ali nisam sigurna,s kompl.prostorom sam na Oni 
ako se ovo sve može,onda dobijemo 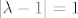
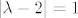

tj.prva jednadžba je kružnica sa središtem u 1 sa radijusom 1,druga jednadžba je kružnica sa središtem u 2 sa radijusom 1,treća jednadžba je kružnica sa središtem u (1,i) - y-os je kompleksna, pa je to zapravo (1,1) - s radijusom 1.
Kada sve tri nacrtamo,vidimo da se te tri kružnice ne sijeku ni u jednoj zajedničkoj točki,pa takav operator ne postoji.
Bilo bi super kad bi mi netko riješio ove nedoumice,i rekao je li ovo točno?
Zadnja promjena: .anchy.; 10:05 ned, 29. 1. 2012; ukupno mijenjano 1 put.
|
|
| [Vrh] |
|
rafaelm
Forumaš(ica)


Pridružen/a: 24. 12. 2006. (13:30:11)
Postovi: (21F)16
Spol: 
Lokacija: Zagreb
|
 Postano: 10:04 ned, 29. 1. 2012 Naslov: Postano: 10:04 ned, 29. 1. 2012 Naslov: |
    |
|
|
[quote=".anchy."][latex]
\lambda \in \sigma(f(A))=f(\sigma(A)) => \abs{\lambda} = 1
[/latex]
[/quote]
Fali apsolutna vrijednost, ti brojevi su po modulu jednaki jedan (tj. na jediničnoj kompkeksnoj kružnici su):
[dtex]|{(\lambda -1)}^{2012}|=1 \ \Rightarrow \ |{\lambda -1}|^{2012}=1 \ \Rightarrow \ |{\lambda -1}|= 1[/dtex]
Sad pročitaš da se [tex]\lambda[/tex] nalazi na kružnici oko 1 radijusa 1.
I tako za ostala dva operatora, pa dobiješ da je [tex]\lambda[/tex] u presjeku tri kružnice, koji je prazan.
EDIT: Vidim da si sve to napravila, ali ne vidim apsolutnu vrijednost.
EDIT2: Sad izgleda OK.
| .anchy. (napisa): | 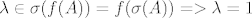
|
Fali apsolutna vrijednost, ti brojevi su po modulu jednaki jedan (tj. na jediničnoj kompkeksnoj kružnici su):
[dtex]|{(\lambda -1)}^{2012}|=1 \ \Rightarrow \ |{\lambda -1}|^{2012}=1 \ \Rightarrow \ |{\lambda -1}|= 1[/dtex]
Sad pročitaš da se [tex]\lambda[/tex] nalazi na kružnici oko 1 radijusa 1.
I tako za ostala dva operatora, pa dobiješ da je [tex]\lambda[/tex] u presjeku tri kružnice, koji je prazan.
EDIT: Vidim da si sve to napravila, ali ne vidim apsolutnu vrijednost.
EDIT2: Sad izgleda OK.
_________________
Rafael Mrđen
Zadnja promjena: rafaelm; 10:06 ned, 29. 1. 2012; ukupno mijenjano 1 put.
|
|
| [Vrh] |
|
.anchy.
Forumaš(ica)

Pridružen/a: 14. 11. 2007. (20:03:46)
Postovi: (1BC)16
Lokacija: Zgb
|
 Postano: 10:06 ned, 29. 1. 2012 Naslov: Postano: 10:06 ned, 29. 1. 2012 Naslov: |
    |
|
|
znam da fale,nisam ih znala staviti,tek sam sad skužila kak :D
hvala ti..A ovaj 2012.korijen iz jednice smijem maknuti,jel?
Eh,da,a 6 je identično kao iz zadaće.
Prvo komentiraš da jer je hermitski,pa posebno i normalan pa postoji ONB u kojoj matrica tog op. ima dijagonalnu matricu gdje su na dijagonali sv.vrijednosti, i zapravo trebamo dokazati da su te sv.vrijednosti sve jednake 1.
Onda koristiš [latex] f(\sigma(A))=\sigma(f(A))[/latex] pa slijedi da je za
[latex]\lambda \in \sigma(A)[/latex] [latex]\lambda^{3333}+\lambda^{333}+\lambda^{33}+\lambda^{3} - 4=0[/latex]
Jedna relna nultočka je 1,a funkcija je strogo rastuća(dokažeš derivacijom),pa je to jedina realna nultočka. Kompleksih nema,jer je operator hermitski. Dakle matrični prikaz od H u toj nekoj bazi je dijagonalna matrica s jedinicama na dijagonali,što je jedinična matrica-
znam da fale,nisam ih znala staviti,tek sam sad skužila kak 
hvala ti..A ovaj 2012.korijen iz jednice smijem maknuti,jel?
Eh,da,a 6 je identično kao iz zadaće.
Prvo komentiraš da jer je hermitski,pa posebno i normalan pa postoji ONB u kojoj matrica tog op. ima dijagonalnu matricu gdje su na dijagonali sv.vrijednosti, i zapravo trebamo dokazati da su te sv.vrijednosti sve jednake 1.
Onda koristiš 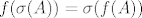 pa slijedi da je za pa slijedi da je za
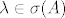 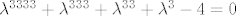
Jedna relna nultočka je 1,a funkcija je strogo rastuća(dokažeš derivacijom),pa je to jedina realna nultočka. Kompleksih nema,jer je operator hermitski. Dakle matrični prikaz od H u toj nekoj bazi je dijagonalna matrica s jedinicama na dijagonali,što je jedinična matrica-
Zadnja promjena: .anchy.; 10:16 ned, 29. 1. 2012; ukupno mijenjano 2 put/a.
|
|
| [Vrh] |
|
rafaelm
Forumaš(ica)


Pridružen/a: 24. 12. 2006. (13:30:11)
Postovi: (21F)16
Spol: 
Lokacija: Zagreb
|
|
| [Vrh] |
|
jackass9
Forumaš(ica)

Pridružen/a: 19. 09. 2009. (10:23:58)
Postovi: (15D)16
Spol: 
Lokacija: pod stolom
|
 Postano: 10:56 ned, 29. 1. 2012 Naslov: Postano: 10:56 ned, 29. 1. 2012 Naslov: |
    |
|
|
[quote=".anchy."]
Eh,da,a 6 je identično kao iz zadaće.
Prvo komentiraš da jer je hermitski,pa posebno i normalan pa postoji ONB u kojoj matrica tog op. ima dijagonalnu matricu gdje su na dijagonali sv.vrijednosti, i zapravo trebamo dokazati da su te sv.vrijednosti sve jednake 1.
Onda koristiš [latex] f(\sigma(A))=\sigma(f(A))[/latex] pa slijedi da je za
[latex]\lambda \in \sigma(A)[/latex] [latex]\lambda^{3333}+\lambda^{333}+\lambda^{33}+\lambda^{3} - 4=0[/latex]
Jedna relna nultočka je 1,a funkcija je strogo rastuća(dokažeš derivacijom),pa je to jedina realna nultočka. Kompleksih nema,jer je operator hermitski. Dakle matrični prikaz od H u toj nekoj bazi je dijagonalna matrica s jedinicama na dijagonali,što je jedinična matrica-[/quote]
ja sam taj šesti riješio na isti način i isto dobio samo dva boda...nisam napisao ovaj prvi "uvodni" dio gdje se komentira da je operator hermitski, normalan, i da postoji m-ca sa svojstvenim vrijednostima na dijagonali i da treba dokazati da su one jednake 1...ostalo mi je sve ok...
zar bi zbog toga skidali 3 boda?
sad ću pisat sve od riječi do riječi sutra :)
| .anchy. (napisa): |
Eh,da,a 6 je identično kao iz zadaće.
Prvo komentiraš da jer je hermitski,pa posebno i normalan pa postoji ONB u kojoj matrica tog op. ima dijagonalnu matricu gdje su na dijagonali sv.vrijednosti, i zapravo trebamo dokazati da su te sv.vrijednosti sve jednake 1.
Onda koristiš 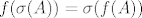 pa slijedi da je za pa slijedi da je za
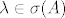 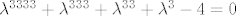
Jedna relna nultočka je 1,a funkcija je strogo rastuća(dokažeš derivacijom),pa je to jedina realna nultočka. Kompleksih nema,jer je operator hermitski. Dakle matrični prikaz od H u toj nekoj bazi je dijagonalna matrica s jedinicama na dijagonali,što je jedinična matrica- |
ja sam taj šesti riješio na isti način i isto dobio samo dva boda...nisam napisao ovaj prvi "uvodni" dio gdje se komentira da je operator hermitski, normalan, i da postoji m-ca sa svojstvenim vrijednostima na dijagonali i da treba dokazati da su one jednake 1...ostalo mi je sve ok...
zar bi zbog toga skidali 3 boda?
sad ću pisat sve od riječi do riječi sutra 
_________________
Nema mozga do malog mozga
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
kolovodja
Gost
|
|
| [Vrh] |
|
|
















