| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
mini
Forumaš(ica)
Pridružen/a: 04. 02. 2009. (14:31:34)
Postovi: (69)16
Spol: 
|
|
| [Vrh] |
|
sz
Forumaš(ica)


Pridružen/a: 26. 01. 2011. (15:17:39)
Postovi: (35)16
|
 Postano: 16:23 pet, 3. 2. 2012 Naslov: Postano: 16:23 pet, 3. 2. 2012 Naslov: |
    |
|
|
U definiciji fje ravnina je podijeljena na 3 dijela dvama paralelnim pravcima ([tex]x = 2y[/tex] i [tex]x = 2y + 2[/tex]) i očito je neprekidnost i diferencijabilnost upitna samo u točkama tih pravaca.
Neprekidnost slijedi iz činjenice da restrikcije fje s obiju strana danih pravaca imaju isti limes u proizvoljnim točkama tih pravaca (npr. za pravac [tex]x = 2y + 2[/tex] limes restrikcije fje f na poluravninu [tex]x > 2y + 2[/tex] u proizvoljnoj točki oblika [tex](2y+2,y)[/tex] je, zbog neprekidnosti te restrikcije, jednak [tex](2y+2)^2-4(2y+2)y=4-4y^2[/tex], ista stvar se dobije za restrikciju na prugi između dvaju pravaca pa imamo neprekidnost u proizvoljnoj točki pravca [tex]x = 2y + 2[/tex], slično za pravac [tex]x = 2y[/tex]).
Ispitajmo diferencijabilnost npr. u točkama oblika [tex](2y+2,y)[/tex]. Znamo da, ako je fja diferencijabilna u točki, onda postoje parcijalne derivacije u toj točki. Gledajmo parcijalnu derivaciju po x:
[dtex]\frac{\partial f}{\partial x}(2y+2,y)=\lim_{h\to 0}\frac{f((2y+2)+h,y)-f(2y+2,y)}{h}.[/dtex]
Ovaj limes postoji akko postoje [tex]\lim_{h\to 0-}\frac{f((2y+2)+h,y)-f(2y+2,y)}{h}[/tex] i [tex]\lim_{h\to 0+}\frac{f((2y+2)+h,y)-f((2y+2),y)}{h}[/tex] i oni su jednaki. Ali ovaj limes slijeva ovisi samo o tome kako fja izgleda na prugi [tex]0 < x-2y \leq 2[/tex], pa ga možemo dobiti kao parcijalnu derivaciju fje [tex]4x-x^2[/tex] po x u promatranoj točki. Slično, limes zdesna možemo dobiti kao parcijalnu derivaciju fje [tex]x^2-4xy[/tex] po x. Zaključujemo da parcijalna derivacija fje f po x u točki [tex](2y+2,y)[/tex] postoji akko su parcijalne derivacije po x tih dviju fja u toj točki jednake. Analogno zaključujemo za parcijalnu derivaciju po y i lako ispada da je jedina točka koja zadovoljava sve [tex](0,-1)[/tex]. Dakle, jedina točka pravca [tex]x=2y+2[/tex] u kojoj bi f mogla biti diferencijabilna je [tex](0, -1)[/tex].
Ali kako je i fja s jedne i fja s druge strane pravca diferencijabilna u točki [tex](0,-1)[/tex], očito je i fja f diferencijabilna u toj točki, s istim diferencijalom (jer on onda očito zadovoljava definiciju diferencijabilnosti fje f (onu s limesom)), znači fja je 100% diferencijabilna u točki [tex](0,-1)[/tex] (nap: tu je jučer bio argument s neprekidnošću parcijalnih derivacija, ali on mi se danas čini nekako mračan...).
Za drugi pravac postupak je isti, dobila sam diferencijabilnost samo u [tex](0,0)[/tex].
Znam da izgleda zbunjujuće, ali ideja je u suštini jednostavna, samo ju je teško precizno i jednostavno objasniti...
U definiciji fje ravnina je podijeljena na 3 dijela dvama paralelnim pravcima ([tex]x = 2y[/tex] i [tex]x = 2y + 2[/tex]) i očito je neprekidnost i diferencijabilnost upitna samo u točkama tih pravaca.
Neprekidnost slijedi iz činjenice da restrikcije fje s obiju strana danih pravaca imaju isti limes u proizvoljnim točkama tih pravaca (npr. za pravac [tex]x = 2y + 2[/tex] limes restrikcije fje f na poluravninu [tex]x > 2y + 2[/tex] u proizvoljnoj točki oblika [tex](2y+2,y)[/tex] je, zbog neprekidnosti te restrikcije, jednak [tex](2y+2)^2-4(2y+2)y=4-4y^2[/tex], ista stvar se dobije za restrikciju na prugi između dvaju pravaca pa imamo neprekidnost u proizvoljnoj točki pravca [tex]x = 2y + 2[/tex], slično za pravac [tex]x = 2y[/tex]).
Ispitajmo diferencijabilnost npr. u točkama oblika [tex](2y+2,y)[/tex]. Znamo da, ako je fja diferencijabilna u točki, onda postoje parcijalne derivacije u toj točki. Gledajmo parcijalnu derivaciju po x:
[dtex]\frac{\partial f}{\partial x}(2y+2,y)=\lim_{h\to 0}\frac{f((2y+2)+h,y)-f(2y+2,y)}{h}.[/dtex]
Ovaj limes postoji akko postoje [tex]\lim_{h\to 0-}\frac{f((2y+2)+h,y)-f(2y+2,y)}{h}[/tex] i [tex]\lim_{h\to 0+}\frac{f((2y+2)+h,y)-f((2y+2),y)}{h}[/tex] i oni su jednaki. Ali ovaj limes slijeva ovisi samo o tome kako fja izgleda na prugi [tex]0 < x-2y \leq 2[/tex], pa ga možemo dobiti kao parcijalnu derivaciju fje [tex]4x-x^2[/tex] po x u promatranoj točki. Slično, limes zdesna možemo dobiti kao parcijalnu derivaciju fje [tex]x^2-4xy[/tex] po x. Zaključujemo da parcijalna derivacija fje f po x u točki [tex](2y+2,y)[/tex] postoji akko su parcijalne derivacije po x tih dviju fja u toj točki jednake. Analogno zaključujemo za parcijalnu derivaciju po y i lako ispada da je jedina točka koja zadovoljava sve [tex](0,-1)[/tex]. Dakle, jedina točka pravca [tex]x=2y+2[/tex] u kojoj bi f mogla biti diferencijabilna je [tex](0, -1)[/tex].
Ali kako je i fja s jedne i fja s druge strane pravca diferencijabilna u točki [tex](0,-1)[/tex], očito je i fja f diferencijabilna u toj točki, s istim diferencijalom (jer on onda očito zadovoljava definiciju diferencijabilnosti fje f (onu s limesom)), znači fja je 100% diferencijabilna u točki [tex](0,-1)[/tex] (nap: tu je jučer bio argument s neprekidnošću parcijalnih derivacija, ali on mi se danas čini nekako mračan...).
Za drugi pravac postupak je isti, dobila sam diferencijabilnost samo u [tex](0,0)[/tex].
Znam da izgleda zbunjujuće, ali ideja je u suštini jednostavna, samo ju je teško precizno i jednostavno objasniti...
|
|
| [Vrh] |
|
markos
Forumaš(ica)
Pridružen/a: 20. 10. 2010. (20:09:26)
Postovi: (B)16
|
|
| [Vrh] |
|
googol
Forumaš(ica)


Pridružen/a: 29. 09. 2011. (21:23:09)
Postovi: (71)16
Spol: 
|
|
| [Vrh] |
|
weeh
Forumaš(ica)
Pridružen/a: 29. 10. 2008. (00:00:53)
Postovi: (32)16
Spol: 
Lokacija: Zagreb
|
 Postano: 17:37 sub, 4. 2. 2012 Naslov: Postano: 17:37 sub, 4. 2. 2012 Naslov: |
    |
|
|
[quote="googol"]Ako je f neprekidna i f(A) kompaktan, je li A kompaktan? Dokazite.[/quote]
Ne nužno.
Pogledaj [latex]f : \mathbb{R} \rightarrow \mathbb{R}, f(x)=sin(x)[/latex], i uzmeš da je [latex]A=\langle -4,4 \rangle[/latex]. Očito je [latex]f(A)=[-1,1][/latex] kompaktan, ali A takav nije kompaktan, ali A nije takav.
Šta god bilo, ne shvačam [latex]sin^{-1}([-1,1])=x[/latex]... Jer je [latex]sin^{-1}([-1,1])=A[/latex] , gdje je A bilokoji skup čija je slika [latex][-1,1][/latex]...
A možda si i upravu, ne znam više :D...
Ipak jesam, jer tebi ne pita da tražim ikakvu prasliku, ovo moje gore je krivo, ali prva argunemtacija mi se čini uredu.
| googol (napisa): | | Ako je f neprekidna i f(A) kompaktan, je li A kompaktan? Dokazite. |
Ne nužno.
Pogledaj 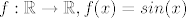 , i uzmeš da je , i uzmeš da je 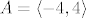 . Očito je . Očito je 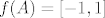 kompaktan, ali A takav nije kompaktan, ali A nije takav. kompaktan, ali A takav nije kompaktan, ali A nije takav.
Šta god bilo, ne shvačam 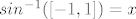 ... Jer je ... Jer je 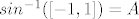 , gdje je A bilokoji skup čija je slika , gdje je A bilokoji skup čija je slika 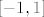 ... ...
A možda si i upravu, ne znam više  ... ...
Ipak jesam, jer tebi ne pita da tražim ikakvu prasliku, ovo moje gore je krivo, ali prva argunemtacija mi se čini uredu.
|
|
| [Vrh] |
|
googol
Forumaš(ica)


Pridružen/a: 29. 09. 2011. (21:23:09)
Postovi: (71)16
Spol: 
|
|
| [Vrh] |
|
mini
Forumaš(ica)
Pridružen/a: 04. 02. 2009. (14:31:34)
Postovi: (69)16
Spol: 
|
|
| [Vrh] |
|
sz
Forumaš(ica)


Pridružen/a: 26. 01. 2011. (15:17:39)
Postovi: (35)16
|
 Postano: 20:57 sub, 4. 2. 2012 Naslov: Postano: 20:57 sub, 4. 2. 2012 Naslov: |
    |
|
|
[quote="markos"]ako može netko riješiti 5.b) zad iz http://web.math.pmf.unizg.hr/nastava/difraf/z2009.pdf
i 1.a) b) c) dokazati iz
http://web.math.pmf.unizg.hr/nastava/difraf/dif/2010-11/popravni.pdf[/quote]
5. b) [tex]f^{-1}(P)[/tex] ne mora biti povezan, primjer je [tex]f:\mathbb{R}\to\mathbb{R},\,f(x):=x^2,\,P=\{1\},\,f^{-1}(P)=\{-1,1\} [/tex], što nije povezano.
1. a) [tex]A_1 \cap A_2[/tex] je zatvoren jer je [tex](A_1 \cap A_2)^c=A_1^c \cup A_2^c[/tex] otvoren kao unija otvorenih; inače, ako se eksplicitno ne traži dokaz, mislim da se činjenica da je presjek zatvorenih skupova zatvoren može koristiti kao poznata tvrdnja.
b) [tex]A_1 \cap A_2[/tex] je nužno ograničen: po definiciji [tex]A_1[/tex] je ograničen akko postoji neka kugla [tex]K[/tex] t. d. [tex]A_1 \subseteq K[/tex], ali onda je i [tex]A_1 \cap A_2 \subseteq A_1 \subseteq K[/tex] pa je, opet po definiciji ograničenosti, [tex]A_1 \cap A_2[/tex] ograničen.
c) Ne, kontraprimjer imaš ovdje: [url]http://degiorgi.math.hr/forum/viewtopic.php?t=17629&start=0#166655[/url]
[quote="googol"]Ako je f neprekidna i f(A) kompaktan, je li A kompaktan? Dokazite.
Rekla bih da nije jer sin(x) poprima vrijednosti [-1,1] sto je kompakatan skup dok sin^-1{[-1,1]} = x, sto nije omedeno.[/quote]
Argumentacija je super, samo što valjda misliš [tex]sin^{-1}([-1,1]) = \mathbb{R}[/tex].
[quote="googol"]Hvala.
http://web.math.pmf.unizg.hr/nastava/difraf/dif/2007-08/DRFVVkol_1.pdf
6. zadatak.
http://web.math.pmf.unizg.hr/nastava/difraf/dif/2006-07/popravni.pdf
zad 8. - rekla bih da nije povezan jer se moze prikazati kao unija dvaju disjunktnih < -bes, 0 > i < 0, bes >[/quote]
6. Očito je neprekidna na [tex]\mathbb{R}^2\backslash\{(x,y)\in\mathbb{R}^2: x^2+y^2=4\}[/tex].
Neka je sad [tex](x,y)[/tex] t. d. [tex]x^2+y^2=4[/tex]. Kako restrikcija fje f na [tex]\{(x,y)\in\mathbb{R}^2: x^2+y^2>4\}[/tex] u točki [tex](x,y)[/tex] ima limes [tex]2(x^2+y^2)=8[/tex], što je različito od [tex]f(x,y)=4[/tex], zaključujemo da f ima prekid u svakoj točki kružnice [tex]x^2+y^2=4[/tex] (jer, ako je fja f neprekidna u nekoj točki, onda svaka njena restrikcija (t.d. je ta točka gomilište njene domene) ima limes u toj točki jednak vrijednosti funkcije u toj točki).
8. Ne vidim baš na što točno misliš... Ako se skup nacrta u ravnini, vidi se da je to dio ravnine oko 0 omeđen dvjema parabolama, i sa slike je odmah očito da je otvoren, nezatvoren (pa i nekompaktan) i povezan. Dokaz je najlakši ako uvjet zapišemo kao [tex]|y|<1-x^2[/tex]. Onda se radi o praslici otvorenog skupa [tex]<-\infty,0>[/tex] po neprekidnoj fji [tex]|y|-1+x^2[/tex] pa je skup otvoren. Nije zatvoren jer je npr. [tex](1,0)[/tex] njegovo gomilište (npr. niz unutra [tex](1-\frac{1}{k},0)\to(1,0)[/tex]) koje nije sadržano u tom skupu. Povezan je jer je povezan putovima: npr. za bilo koje dvije točke iz A segment koji spaja te dvije točke je očito u A (a on je slika nekog puta u A koji povezuje te dvije točke), to se valjda može i formalno raspisati...
5. b) [tex]f^{-1}(P)[/tex] ne mora biti povezan, primjer je [tex]f:\mathbb{R}\to\mathbb{R},\,f(x):=x^2,\,P=\{1\},\,f^{-1}(P)=\{-1,1\} [/tex], što nije povezano.
1. a) [tex]A_1 \cap A_2[/tex] je zatvoren jer je [tex](A_1 \cap A_2)^c=A_1^c \cup A_2^c[/tex] otvoren kao unija otvorenih; inače, ako se eksplicitno ne traži dokaz, mislim da se činjenica da je presjek zatvorenih skupova zatvoren može koristiti kao poznata tvrdnja.
b) [tex]A_1 \cap A_2[/tex] je nužno ograničen: po definiciji [tex]A_1[/tex] je ograničen akko postoji neka kugla [tex]K[/tex] t. d. [tex]A_1 \subseteq K[/tex], ali onda je i [tex]A_1 \cap A_2 \subseteq A_1 \subseteq K[/tex] pa je, opet po definiciji ograničenosti, [tex]A_1 \cap A_2[/tex] ograničen.
c) Ne, kontraprimjer imaš ovdje: http://degiorgi.math.hr/forum/viewtopic.php?t=17629&start=0#166655
| googol (napisa): | Ako je f neprekidna i f(A) kompaktan, je li A kompaktan? Dokazite.
Rekla bih da nije jer sin(x) poprima vrijednosti [-1,1] sto je kompakatan skup dok sin^-1{[-1,1]} = x, sto nije omedeno. |
Argumentacija je super, samo što valjda misliš [tex]sin^{-1}([-1,1]) = \mathbb{R}[/tex].
6. Očito je neprekidna na [tex]\mathbb{R}^2\backslash\{(x,y)\in\mathbb{R}^2: x^2+y^2=4\}[/tex].
Neka je sad [tex](x,y)[/tex] t. d. [tex]x^2+y^2=4[/tex]. Kako restrikcija fje f na [tex]\{(x,y)\in\mathbb{R}^2: x^2+y^2>4\}[/tex] u točki [tex](x,y)[/tex] ima limes [tex]2(x^2+y^2)=8[/tex], što je različito od [tex]f(x,y)=4[/tex], zaključujemo da f ima prekid u svakoj točki kružnice [tex]x^2+y^2=4[/tex] (jer, ako je fja f neprekidna u nekoj točki, onda svaka njena restrikcija (t.d. je ta točka gomilište njene domene) ima limes u toj točki jednak vrijednosti funkcije u toj točki).
8. Ne vidim baš na što točno misliš... Ako se skup nacrta u ravnini, vidi se da je to dio ravnine oko 0 omeđen dvjema parabolama, i sa slike je odmah očito da je otvoren, nezatvoren (pa i nekompaktan) i povezan. Dokaz je najlakši ako uvjet zapišemo kao [tex]|y|<1-x^2[/tex]. Onda se radi o praslici otvorenog skupa [tex]←\infty,0>[/tex] po neprekidnoj fji [tex]|y|-1+x^2[/tex] pa je skup otvoren. Nije zatvoren jer je npr. [tex](1,0)[/tex] njegovo gomilište (npr. niz unutra [tex](1-\frac{1}{k},0)\to(1,0)[/tex]) koje nije sadržano u tom skupu. Povezan je jer je povezan putovima: npr. za bilo koje dvije točke iz A segment koji spaja te dvije točke je očito u A (a on je slika nekog puta u A koji povezuje te dvije točke), to se valjda može i formalno raspisati...
|
|
| [Vrh] |
|
markos
Forumaš(ica)
Pridružen/a: 20. 10. 2010. (20:09:26)
Postovi: (B)16
|
|
| [Vrh] |
|
googol
Forumaš(ica)


Pridružen/a: 29. 09. 2011. (21:23:09)
Postovi: (71)16
Spol: 
|
 Postano: 22:02 sub, 4. 2. 2012 Naslov: Postano: 22:02 sub, 4. 2. 2012 Naslov: |
    |
|
|
http://web.math.pmf.unizg.hr/nastava/difraf/dif/2008-09/popravni.pdf
Po n-ti put, 1.a), korak po korak. Jasna mi je ideja, no nikako da to lijepo, matematicki zapisem.
http://web.math.pmf.unizg.hr/nastava/difraf/dif/2007-08/DRFVVkol_1.pdf
5. zad.
http://web.math.pmf.unizg.hr/nastava/difraf/dif/2006-07/zavrsni.pdf
1. i 5.
2. - rekla bih da je 0<=x<=1 i 0<=y<=1, i povezan jer jer se ne moze prikazati kao unija dva disjunktna otvorena skupa, a dokaz bi isla s pretp. suprotno.
http://web.math.pmf.unizg.hr/nastava/difraf/dif/2007-08/DRFVVzavrsni.pdf
2. razspise se na kompoziciju f-ja?
http://web.math.pmf.unizg.hr/nastava/difraf/z2009.pdf
1. je li povezan?
http://web.math.pmf.unizg.hr/nastava/difraf/dif/2009-10/zavrsni.pdf
4. b i c
http://web.math.pmf.unizg.hr/nastava/difraf/dif/2010-11/popravni.pdf
2.b
Iz ovogodisnjeh zavrsnog:
Zadana je f:R^2 -> R s
f (x, y) = x^2 * y^3 / (x^2 + y^2)^2 + 2x + y za (x,y) != (0,0)
0, (x,y) = (0,0)
Dokazite da je f-ja neprekidna, ali nije dfb.
A = K [0,2]\K(0,1) i neka je f je neprekidna.
Je li f(a) nuzno zatvoren ?
ogranicen?
kompaktan
povezan
povezan putovima?
Puno, puno hvala.
http://web.math.pmf.unizg.hr/nastava/difraf/dif/2008-09/popravni.pdf
Po n-ti put, 1.a), korak po korak. Jasna mi je ideja, no nikako da to lijepo, matematicki zapisem.
http://web.math.pmf.unizg.hr/nastava/difraf/dif/2007-08/DRFVVkol_1.pdf
5. zad.
http://web.math.pmf.unizg.hr/nastava/difraf/dif/2006-07/zavrsni.pdf
1. i 5.
2. - rekla bih da je 0⇐x⇐1 i 0⇐y⇐1, i povezan jer jer se ne moze prikazati kao unija dva disjunktna otvorena skupa, a dokaz bi isla s pretp. suprotno.
http://web.math.pmf.unizg.hr/nastava/difraf/dif/2007-08/DRFVVzavrsni.pdf
2. razspise se na kompoziciju f-ja?
http://web.math.pmf.unizg.hr/nastava/difraf/z2009.pdf
1. je li povezan?
http://web.math.pmf.unizg.hr/nastava/difraf/dif/2009-10/zavrsni.pdf
4. b i c
http://web.math.pmf.unizg.hr/nastava/difraf/dif/2010-11/popravni.pdf
2.b
Iz ovogodisnjeh zavrsnog:
Zadana je f:R^2 → R s
f (x, y) = x^2 * y^3 / (x^2 + y^2)^2 + 2x + y za (x,y) != (0,0)
0, (x,y) = (0,0)
Dokazite da je f-ja neprekidna, ali nije dfb.
A = K [0,2]\K(0,1) i neka je f je neprekidna.
Je li f(a) nuzno zatvoren ?
ogranicen?
kompaktan
povezan
povezan putovima?
Puno, puno hvala.
|
|
| [Vrh] |
|
tamusil
Forumaš(ica)
Pridružen/a: 04. 02. 2012. (17:48:39)
Postovi: (B)16
|
 Postano: 0:15 ned, 5. 2. 2012 Naslov: Postano: 0:15 ned, 5. 2. 2012 Naslov: |
    |
|
|
Evo, da i ja napišem prvi post i da malo se igram s LaTeXom.
Nisam sve rješio u nadi da će vam i neko drugi pomoći jer stvarno imam puno za pisat.
08/09 1.a) + malo sam si prilagodio oznake
[latex]\|x-y\| = d(x,y)[/latex] , [latex]r>0[/latex] i [latex]c \in \mathbb{R}^n[/latex]
[latex]K=\{ x \in \mathbb{R}^n | d(x,c) \leq r \}[/latex] i pokazujemo da je K zatvoren skup. Po definiciji je onda [latex]K^{c}=\{ x \in \mathbb{R}^n | d(x,c) > r \}[/latex] otvoren i to pokazujemo. Uzmimo proizvoljan [latex] y \in \mathbb{R}^n[/latex] i definiramo [latex]r_1=d(c,y)-r>0[/latex]. Tvrdimo [latex] K(y,r_1) \subset K^c[/latex]. Sada u to ime uzmimo [latex] z \in K(y,r_1) [/latex]. Zbog [latex]d(z,c)=d(c,z) \geq d(c,y) - d(y,z) > d(c,y) -r_1 = r[/latex]. Pa slijedi da je [latex] z \in K^c [/latex], pa je taj skup otvoren, a [latex] K [/latex] zatvoren.
07.
5)
Imamo [latex]f : \mathbb{R}^n \rightarrow \mathbb{R}^m [/latex] koja je diferencijabilna i postoji operator [latex]A[/latex] takav da je [latex] Df(x) = A , \forall x[/latex].
komentar - Kako je ovo konstantna matrica onda je ona diferencijabila i diferencijal je [latex] 0 [/latex]. To se vidi iz definiciji odmah jer [latex] \frac{Df(x) - Df(c) - K(x-c)}{x-c} =\frac{A-A-K(x-c)}{x-c}=\frac{K(x-c)}{x-c} [/latex]. Vidi se da će ovo u limesu kada x teži prema c biti 0 ako je K nuloperator.
Koristimo Taylorov tm srednje vrijednosti. Kako smo u [latex] R^n [/latex] svaki [latex] \[x,c\][/latex] je u [latex]R^n [/latex] (želim reć da su zadovoljene pretpostavke tm). Tada znamo da postoji [latex] \eta [/latex] između x i c takva da vrijedi sljedeće:
[latex] f(x) = f(c) + Df(c)(x-c) + \frac{D^2f(\eta)}{2}(x-c,x-c)[/latex]. Zbog komentara prije sljedi da je zadnji član ove sume nula. Pa dobivamo [latex]f(x)=f(c)+Df(c)(x-c)= f(c)+A(x-c)=Ax+f(c)-Ac[/latex]. Uz oznaku da je [latex]b=f(c)-Ac[/latex] to je upravo šta se traži.
I nažalost zadnji jer idem spavati...
Ovako je glasio.
[latex]A,B \subseteq \mathbb{R}^n[/latex] otvoreni. Treba se pokazat da su i unija i presjek otvoreni.
- unija
Uzmimo proizvoljan [latex] x \in A \bigcup B [/latex]. Tada je [latex]x\in A[/latex] ili [latex]x\in B[/latex]. BSOMP da je [latex]x\in A[/latex]. No kako je A otvoren postoji [latex]K(x,r) \subseteq A \subset A \bigcup B[/latex].
-presjek
Ako je presjek A i B prazan , tvrdnja vrijedi.
Neka je [latex]x \in A \bigcap B \neq \emptyset[/latex]. Tj. [latex]x \in A[/latex] i [latex]x \in B[/latex]. Zbog otvorenosti skupova A i B postoje [latex]r_1,r_2 > 0 [/latex] t.d. je [latex]K(x,r_1) \subseteq A[/latex] i [latex]K(x,r_2) \subseteq B[/latex]. Uzmemo da je [latex]r=min\{r_1,r_2\}[/latex]. Pa je [latex]K(x,r) \subseteq A[/latex] i [latex]K(x,r) \subseteq B[/latex] , a od tuda slijedi da je [latex]K(x,r) \subseteq A \bigcap B[/latex]. Pa je presjek otvoren isto.
Sretno na ispitma :)
Evo, da i ja napišem prvi post i da malo se igram s LaTeXom.
Nisam sve rješio u nadi da će vam i neko drugi pomoći jer stvarno imam puno za pisat.
08/09 1.a) + malo sam si prilagodio oznake
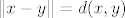 , , 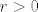 i i 
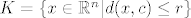 i pokazujemo da je K zatvoren skup. Po definiciji je onda i pokazujemo da je K zatvoren skup. Po definiciji je onda 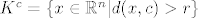 otvoren i to pokazujemo. Uzmimo proizvoljan otvoren i to pokazujemo. Uzmimo proizvoljan 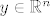 i definiramo i definiramo 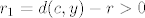 . Tvrdimo . Tvrdimo 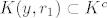 . Sada u to ime uzmimo . Sada u to ime uzmimo 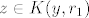 . Zbog . Zbog  . Pa slijedi da je . Pa slijedi da je  , pa je taj skup otvoren, a , pa je taj skup otvoren, a 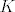 zatvoren. zatvoren.
07.
5)
Imamo 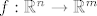 koja je diferencijabilna i postoji operator koja je diferencijabilna i postoji operator  takav da je takav da je 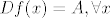 . .
komentar - Kako je ovo konstantna matrica onda je ona diferencijabila i diferencijal je 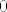 . To se vidi iz definiciji odmah jer . To se vidi iz definiciji odmah jer 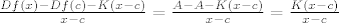 . Vidi se da će ovo u limesu kada x teži prema c biti 0 ako je K nuloperator. . Vidi se da će ovo u limesu kada x teži prema c biti 0 ako je K nuloperator.
Koristimo Taylorov tm srednje vrijednosti. Kako smo u 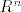 svaki svaki 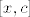 je u je u 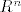 (želim reć da su zadovoljene pretpostavke tm). Tada znamo da postoji (želim reć da su zadovoljene pretpostavke tm). Tada znamo da postoji 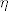 između x i c takva da vrijedi sljedeće: između x i c takva da vrijedi sljedeće:
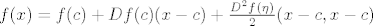 . Zbog komentara prije sljedi da je zadnji član ove sume nula. Pa dobivamo . Zbog komentara prije sljedi da je zadnji član ove sume nula. Pa dobivamo 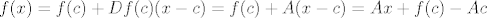 . Uz oznaku da je . Uz oznaku da je 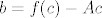 to je upravo šta se traži. to je upravo šta se traži.
I nažalost zadnji jer idem spavati...
Ovako je glasio.
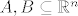 otvoreni. Treba se pokazat da su i unija i presjek otvoreni. otvoreni. Treba se pokazat da su i unija i presjek otvoreni.
- unija
Uzmimo proizvoljan 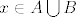 . Tada je . Tada je 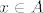 ili ili 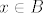 . BSOMP da je . BSOMP da je 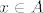 . No kako je A otvoren postoji . No kako je A otvoren postoji 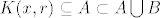 . .
-presjek
Ako je presjek A i B prazan , tvrdnja vrijedi.
Neka je  . Tj. . Tj. 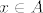 i i 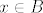 . Zbog otvorenosti skupova A i B postoje . Zbog otvorenosti skupova A i B postoje 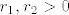 t.d. je t.d. je 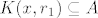 i i 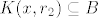 . Uzmemo da je . Uzmemo da je 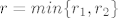 . Pa je . Pa je 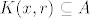 i i 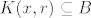 , a od tuda slijedi da je , a od tuda slijedi da je  . Pa je presjek otvoren isto. . Pa je presjek otvoren isto.
Sretno na ispitma 
|
|
| [Vrh] |
|
mango
Forumaš(ica)

Pridružen/a: 02. 02. 2012. (21:26:21)
Postovi: (F)16
|
|
| [Vrh] |
|
sz
Forumaš(ica)


Pridružen/a: 26. 01. 2011. (15:17:39)
Postovi: (35)16
|
 Postano: 12:10 ned, 5. 2. 2012 Naslov: Postano: 12:10 ned, 5. 2. 2012 Naslov: |
    |
|
|
[quote="googol"]http://web.math.pmf.unizg.hr/nastava/difraf/dif/2007-08/DRFVVkol_1.pdf
5. zad. [/quote]
a) Svaki Cauchyjev niz u A ujedno je Cauchyjev niz u [tex]\mathbb{R}^n[/tex] pa konvergira u [tex]\mathbb{R}^n[/tex] (jer je [tex]\mathbb{R}^n[/tex] potpun). Ali kako je A zatvoren, svaki niz u A koji konvergira u [tex]\mathbb{R}^n[/tex] ima limes u A, tj. konvergira u A, pa je odgovor da i zatvorenost je dovoljna (ili se jednostavno pozoveš na Prop. 4.25).
b) f i g su neprekidne na kompaktnim domenama pa postižu minimum i maksimum. h ga ne mora postizati, npr. ako je [tex]f(x,y):=x[/tex], infimum slike od h je 2, ali on se nigdje ne postiže.
[quote="google"]http://web.math.pmf.unizg.hr/nastava/difraf/dif/2006-07/zavrsni.pdf
1. i 5.
2. - rekla bih da je 0<=x<=1 i 0<=y<=1, i povezan jer jer se ne moze prikazati kao unija dva disjunktna otvorena skupa, a dokaz bi isla s pretp. suprotno. [/quote]
1. Teorem 4.23.
2. Malo drugačije zapisano, radi se o skupu [tex]\{(x,y)\in\mathbb{R}^2: x^2+y^2\leq1\}[/tex], tj. o A = [tex]\overline{K}(0,1)[/tex], kompaktnost se lagano pokaže (zatvorenost je, za općenitiji slučaj, raspisana 2 posta iznad); povezanost može npr. iz povezanosti putevima: za [tex]x,y\in A[/tex] [tex]p:[0,1]\to\mathbb{R}^2,\,p(t):=x+t(y-x)=(1-t)x+ty[/tex] je put od x do y u A; stvarno, svaka točka slike je u A: [dtex]||(1-t)x+ty||\leq(1-t)||x||+t||y||\leq(1-t)\cdot1+t\cdot1=1.[/dtex]
[quote="googol"]http://web.math.pmf.unizg.hr/nastava/difraf/dif/2007-08/DRFVVzavrsni.pdf
2. razspise se na kompoziciju f-ja? [/quote]
Da, klasično baratanje s diferencijalom kompozicije i skalarnog produkta, čini mi se da ispadne [tex]Df(x,y)(s,t)=2\cos(||2x+y||^2+||y||^2)((2s+t|2x+y)+(t|y))[/tex].
[quote="googol"]http://web.math.pmf.unizg.hr/nastava/difraf/z2009.pdf
1. je li povezan? [/quote]
Ako se točno nacrta slika, vidi se da nije povezan - sastoji se od kvadrata s vrhovima [tex](1,0),(0,1),(-1,0),(0,-1)[/tex] i kružnice polumjera [tex]\frac{1}{2}[/tex] sa središtem u ishodištu. Svaka točka tog kvadrata od ishodišta je udaljena barem za [tex]\frac{1}{\sqrt{2}}>\frac{1}{2}[/tex].
[quote="googol"]http://web.math.pmf.unizg.hr/nastava/difraf/dif/2009-10/zavrsni.pdf
4. b i c [/quote]
4. b) Ako su A i B zatvoreni, tj. njihovi komplementi otvoreni, onda je [tex](A\cup B)^c=A^c\cap B^c[/tex] otvoren kao presjek otvorenih (što je tamusil dokazao dva posta iznad), slično za [tex](A\cap B)^c=A^c\cup B^c[/tex].
c) Najlakše mi se čini koristeći katrakterizaciju zatvorenosti pomoću nizova: S je zatvoren akko svaki niz u S koji konvergira u [tex]\mathbb{R}^n[/tex] ima limes u S.
Pa neka je sad [tex](x_k,y_k)[/tex] niz u [tex]A \times B[/tex] koji konvergira u [tex]\mathbb{R}^{m+n}[/tex]. Onda svaki od njegovih koordinatnih nizova konvergira u [tex]\mathbb{R}[/tex], pa [tex](x_k)[/tex] konvergira u [tex]\mathbb{R}^m[/tex] i [tex](y_k)[/tex] konvergira u [tex]\mathbb{R}^n[/tex]. Zbog zatvorenosti od A i B slijedi da su njihovi limesi (zovimo ih x i y) [tex]x\in A[/tex] i [tex]y\in B[/tex], tj. [tex]\lim_{k\to\infty}(x_k,y_k)=(x,y)\in A\times B[/tex] pa je [tex]A\times B[/tex] zatvoren.
Obrat ne vrijedi jer jedan od skupova A i B može biti prazan, npr. za [tex]A=<0,1>,\,B=\emptyset[/tex], [tex]A\times B=\emptyset[/tex] je zatvoren, ali A nije zatvoren.
Evo i upute za toliko traženi 2.b) sa [url]http://web.math.pmf.unizg.hr/nastava/difraf/dif/2010-11/popravni.pdf[/url]:
prvo pogledajmo kako izgleda fja [tex]f+g[/tex]:
[dtex](f+g)(x,y)=\begin{cases}
5(x+y),\qquad y\geq x \quad\&\quad y\leq -x\\
5(x+y)+1, \qquad y\geq x \quad\&\quad y>x\\
4x+6y, \qquad y<x\quad\&\quad y\leq -x\\
4x+6y+1,\qquad y < x \quad\&\quad y>-x.\end{cases}[/dtex]
Sve se puno ljepše vidi ako si nacrtate ovu podjelu ravnine; odmah je jasno da u svim točkama pravca [tex]y=-x[/tex] fja ima prekid. Za točke [tex](x,x), x\neq 0[/tex] nema prekida, ali fja u njima nije diferencijabilna (jer si parcijalne derivacije ovih restrikcija s jedne i druge strane pravca ne pašu).
Ovogodišnji završni - zadatak s neprekidnosti i diferencijabilnosti:
neprekidnost u [tex](0,0)[/tex] ocjenom
[dtex]|\frac{x^2 y^3}{(x^2+y^2)^2}+2x+y|\leq|y|\frac{x^2}{x^2+y^2}\frac{y^2}{x^2+y^2}+2|x|+|y|\leq1\cdot1\cdot |y|+2|x|+|y|.[/dtex]
A onda po definiciji izračunamo parcijalne derivacije u [tex](0,0)[/tex] (2 i 1 ako se ne varam) koje nam daju jedinog mogućeg kandidata za diferencijal, a onda pokažemo da taj kandidat ne zadovoljava definiciju diferencijala (onaj dugi limes nije 0) pa f nije diferencijabilna u (0,0).
Ovaj skup iz završnoga mi izgleda kao kružni vijenac (s "uključenim" rubovima), očito je kompaktan i povezan putevima pa ga neprekidna fja nosi u kompaktan skup povezan putevima, dakle zatvoren, ograničen, povezan i putevima povezan skup.
| googol (napisa): | http://web.math.pmf.unizg.hr/nastava/difraf/dif/2007-08/DRFVVkol_1.pdf
5. zad. |
a) Svaki Cauchyjev niz u A ujedno je Cauchyjev niz u [tex]\mathbb{R}^n[/tex] pa konvergira u [tex]\mathbb{R}^n[/tex] (jer je [tex]\mathbb{R}^n[/tex] potpun). Ali kako je A zatvoren, svaki niz u A koji konvergira u [tex]\mathbb{R}^n[/tex] ima limes u A, tj. konvergira u A, pa je odgovor da i zatvorenost je dovoljna (ili se jednostavno pozoveš na Prop. 4.25).
b) f i g su neprekidne na kompaktnim domenama pa postižu minimum i maksimum. h ga ne mora postizati, npr. ako je [tex]f(x,y):=x[/tex], infimum slike od h je 2, ali on se nigdje ne postiže.
| google (napisa): | http://web.math.pmf.unizg.hr/nastava/difraf/dif/2006-07/zavrsni.pdf
1. i 5.
2. - rekla bih da je 0⇐x⇐1 i 0⇐y⇐1, i povezan jer jer se ne moze prikazati kao unija dva disjunktna otvorena skupa, a dokaz bi isla s pretp. suprotno. |
1. Teorem 4.23.
2. Malo drugačije zapisano, radi se o skupu [tex]\{(x,y)\in\mathbb{R}^2: x^2+y^2\leq1\}[/tex], tj. o A = [tex]\overline{K}(0,1)[/tex], kompaktnost se lagano pokaže (zatvorenost je, za općenitiji slučaj, raspisana 2 posta iznad); povezanost može npr. iz povezanosti putevima: za [tex]x,y\in A[/tex] [tex]p:[0,1]\to\mathbb{R}^2,\,p(t):=x+t(y-x)=(1-t)x+ty[/tex] je put od x do y u A; stvarno, svaka točka slike je u A: [dtex]||(1-t)x+ty||\leq(1-t)||x||+t||y||\leq(1-t)\cdot1+t\cdot1=1.[/dtex]
| googol (napisa): | http://web.math.pmf.unizg.hr/nastava/difraf/dif/2007-08/DRFVVzavrsni.pdf
2. razspise se na kompoziciju f-ja? |
Da, klasično baratanje s diferencijalom kompozicije i skalarnog produkta, čini mi se da ispadne [tex]Df(x,y)(s,t)=2\cos(||2x+y||^2+||y||^2)((2s+t|2x+y)+(t|y))[/tex].
| googol (napisa): | http://web.math.pmf.unizg.hr/nastava/difraf/z2009.pdf
1. je li povezan? |
Ako se točno nacrta slika, vidi se da nije povezan - sastoji se od kvadrata s vrhovima [tex](1,0),(0,1),(-1,0),(0,-1)[/tex] i kružnice polumjera [tex]\frac{1}{2}[/tex] sa središtem u ishodištu. Svaka točka tog kvadrata od ishodišta je udaljena barem za [tex]\frac{1}{\sqrt{2}}>\frac{1}{2}[/tex].
| googol (napisa): | http://web.math.pmf.unizg.hr/nastava/difraf/dif/2009-10/zavrsni.pdf
4. b i c |
4. b) Ako su A i B zatvoreni, tj. njihovi komplementi otvoreni, onda je [tex](A\cup B)^c=A^c\cap B^c[/tex] otvoren kao presjek otvorenih (što je tamusil dokazao dva posta iznad), slično za [tex](A\cap B)^c=A^c\cup B^c[/tex].
c) Najlakše mi se čini koristeći katrakterizaciju zatvorenosti pomoću nizova: S je zatvoren akko svaki niz u S koji konvergira u [tex]\mathbb{R}^n[/tex] ima limes u S.
Pa neka je sad [tex](x_k,y_k)[/tex] niz u [tex]A \times B[/tex] koji konvergira u [tex]\mathbb{R}^{m+n}[/tex]. Onda svaki od njegovih koordinatnih nizova konvergira u [tex]\mathbb{R}[/tex], pa [tex](x_k)[/tex] konvergira u [tex]\mathbb{R}^m[/tex] i [tex](y_k)[/tex] konvergira u [tex]\mathbb{R}^n[/tex]. Zbog zatvorenosti od A i B slijedi da su njihovi limesi (zovimo ih x i y) [tex]x\in A[/tex] i [tex]y\in B[/tex], tj. [tex]\lim_{k\to\infty}(x_k,y_k)=(x,y)\in A\times B[/tex] pa je [tex]A\times B[/tex] zatvoren.
Obrat ne vrijedi jer jedan od skupova A i B može biti prazan, npr. za [tex]A=<0,1>,\,B=\emptyset[/tex], [tex]A\times B=\emptyset[/tex] je zatvoren, ali A nije zatvoren.
Evo i upute za toliko traženi 2.b) sa http://web.math.pmf.unizg.hr/nastava/difraf/dif/2010-11/popravni.pdf:
prvo pogledajmo kako izgleda fja [tex]f+g[/tex]:
[dtex](f+g)(x,y)=\begin{cases}
5(x+y),\qquad y\geq x \quad\&\quad y\leq -x\\
5(x+y)+1, \qquad y\geq x \quad\&\quad y>x\\
4x+6y, \qquad y<x\quad\&\quad y\leq -x\\
4x+6y+1,\qquad y < x \quad\&\quad y>-x.\end{cases}[/dtex]
Sve se puno ljepše vidi ako si nacrtate ovu podjelu ravnine; odmah je jasno da u svim točkama pravca [tex]y=-x[/tex] fja ima prekid. Za točke [tex](x,x), x\neq 0[/tex] nema prekida, ali fja u njima nije diferencijabilna (jer si parcijalne derivacije ovih restrikcija s jedne i druge strane pravca ne pašu).
Ovogodišnji završni - zadatak s neprekidnosti i diferencijabilnosti:
neprekidnost u [tex](0,0)[/tex] ocjenom
[dtex]|\frac{x^2 y^3}{(x^2+y^2)^2}+2x+y|\leq|y|\frac{x^2}{x^2+y^2}\frac{y^2}{x^2+y^2}+2|x|+|y|\leq1\cdot1\cdot |y|+2|x|+|y|.[/dtex]
A onda po definiciji izračunamo parcijalne derivacije u [tex](0,0)[/tex] (2 i 1 ako se ne varam) koje nam daju jedinog mogućeg kandidata za diferencijal, a onda pokažemo da taj kandidat ne zadovoljava definiciju diferencijala (onaj dugi limes nije 0) pa f nije diferencijabilna u (0,0).
Ovaj skup iz završnoga mi izgleda kao kružni vijenac (s "uključenim" rubovima), očito je kompaktan i povezan putevima pa ga neprekidna fja nosi u kompaktan skup povezan putevima, dakle zatvoren, ograničen, povezan i putevima povezan skup.
|
|
| [Vrh] |
|
googol
Forumaš(ica)


Pridružen/a: 29. 09. 2011. (21:23:09)
Postovi: (71)16
Spol: 
|
|
| [Vrh] |
|
mini
Forumaš(ica)
Pridružen/a: 04. 02. 2009. (14:31:34)
Postovi: (69)16
Spol: 
|
 Postano: 12:55 ned, 5. 2. 2012 Naslov: Postano: 12:55 ned, 5. 2. 2012 Naslov: |
    |
|
|
googol, bila sam kod tambace i objasnio mi je sto zapravo treba raditi kod takvih zadataka (u ovom slucaju je to bio kruzni vijenac). trebas dokazati! da je ktuzni vijenac kompaktan i povezan skup, i onda se samo pozivas na teoreme sa predavanja. npr. ako je A kompaktan i f nepr. onda je f(A) kompaktan. i to je sve. a ja krelac dokazivala te teoreme sto naravno nije trebalo.
ja imam pitanje vezano za taylorov teorem, tj kadtreba izracunati ostatak. npr zadatak s drugog kolokvija: f(x,y)=e^(xy)+x^2+y. izracunat taylorov polinom 1. stupnja u (1,2) i izracunat ostatak.
sz, puno hvala odgovorima!
googol, bila sam kod tambace i objasnio mi je sto zapravo treba raditi kod takvih zadataka (u ovom slucaju je to bio kruzni vijenac). trebas dokazati! da je ktuzni vijenac kompaktan i povezan skup, i onda se samo pozivas na teoreme sa predavanja. npr. ako je A kompaktan i f nepr. onda je f(A) kompaktan. i to je sve. a ja krelac dokazivala te teoreme sto naravno nije trebalo.
ja imam pitanje vezano za taylorov teorem, tj kadtreba izracunati ostatak. npr zadatak s drugog kolokvija: f(x,y)=e^(xy)+x^2+y. izracunat taylorov polinom 1. stupnja u (1,2) i izracunat ostatak.
sz, puno hvala odgovorima!
|
|
| [Vrh] |
|
sz
Forumaš(ica)


Pridružen/a: 26. 01. 2011. (15:17:39)
Postovi: (35)16
|
 Postano: 15:01 ned, 5. 2. 2012 Naslov: Postano: 15:01 ned, 5. 2. 2012 Naslov: |
    |
|
|
Još mi je tjedan dana posao da vas spašavam. 8)
Da, kad vas se takve stvari pitaju na kolokviju, nije dovoljno samo napisati "očito je", posebno ako se negdje spominje "obrazložite sve tvrdnje" ili, još gore, "sve tvrdnje dokažite". Za ovaj bi kružni vijenac recimo bilo OK napisati da je ograničen jer je sadržan u kugli K(0, 3); za zatvorenost je, ako se ne traži 100%-tni dokaz, dovoljno skicirati skup i onda reći da je sa slike očito da za svaku točku komplementa postoji neka otvorena kugla sa središtem u njoj koja je sadržana u komplementu (možda na skici nacrtati tu kuglu za par točaka, da se vidi da je tebi to 100% jasno), što znači da je komplement otvoren pa je skup po definiciji zatvoren; ovo ipak još uvijek nije dovoljno ako se traži precizan dokaz - trebalo bi sve raspisati.
Preciznije bi bilo npr. promatrati proizvoljan niz [tex](x_k,y_k)[/tex] u tom skupu koji konvergira u [tex]\mathbb{R}^2[/tex] prema [tex](x,y)[/tex]. Onda vrijedi [tex]1\leq x_k^2+y_k^2\leq 4[/tex] pa, kad pustimo limes na tu nejednakost, iskoristivši da koordinatni nizovi konvergiraju prema x i y, imamo [tex]1\leq x^2+y^2\leq 4[/tex], pa je [tex](x,y)[/tex] u kružnom vijencu i po karakterizaciji zatvorenosti pomoću limesa imamo da je skup zatvoren.
Ili, najelegantnije, uočiti da je taj kružni vijenac zapravo [tex]f([1,2]\times[0,2\pi])[/tex] za fju [tex]f(r,\phi)=(r\cos\phi, r\sin\phi)[/tex] (polarne koordinate), dakle slika zatvorenog pravokutnika, za koji i ptice na grani znaju da je kompaktan, po neprekidnoj fji f, pa je kompaktan. Polarne koordinate mogu se lijepo iskoristiti za takve stvari uvijek kad imamo nekakve kružne skupove.
Sigurno ima još načina. Što je dokaz precizniji, to bolje.
Za povezanost opet možemo iskoristiti gornju fju f jer neprekidna fja povezane skupove (npr. pravokutnike) nosi u povezane, a pravokutnik je povezan jer je povezan putovima (npr. svake dvije točke povezuje put koji prođe po segmentu od jedne do druge).
Ili direktno pokažemo da je kružni vijenac povezan putovima - npr. za bilo koje dvije točke uočimo da se nalaze na koncentričnim kružnicama sa središtem u ishodištu, a put bismo onda mogli konstruirati tako da prvo iz jedne točke, u smjeru radijvektora te točke, prijeđe na kružnicu na kojoj je druga točka, a onda po toj kružnici doputuje do druge točke. Valjda bi se dale napisati i neke precizne jednadžbe, ali i ideje se cijene... :wink:
To je glavni dio posla. Ako i ne znaš precizan dokaz, bar u jednoj rečenici obrazloži zašto je to tebi jasno.
http://web.math.pmf.unizg.hr/nastava/difraf/dif/2009-10-kol1/kol1_0910.pdf
6. a) Koordinatne fje su neprekidne jer su to linearne kombinacije nekih projekcija blablabla...
b) [tex]d(f(x_1,x_2,x_3),f(y_1,y_2,y_3))[/tex]
[tex]=||(x_1-x_3,x_1+x_2)-(y_1-y_3, y_1+y_2)||[/tex]
[tex]=||(x_1-y_1,0)+(-x_3+y_3,0)+(0,x_1-y_1)+(0,x_2-y_2)||[/tex]
[tex]\leq||(x_1-y_1,0)||+||(-x_3+y_3,0)||+||(0,x_1-y_1)||+||(0,x_2-y_2)||[/tex]
[tex]=|x_1-y_1|+|x_3-y_3|+|x_1-y_1|+|x_2-y_2|[/tex]
[tex]\leq4\sqrt{(x_1-y_1)^2+(x_2-y_2)^2+(x_3-y_3)^2}[/tex]
[tex]=4d((x_1,x_2,x_3),(y_1,y_2,y_3))[/tex]
pa ako za zadani [tex]\epsilon>0[/tex] uzmemo [tex]\delta=\frac{\epsilon}{4}[/tex], imamo uniformnu neprekidnost po definiciji.
Sa c) valjda nema problema, a onda za d) možemo iskoristiti [tex]\frac{\partial f}{\partial v}(c)=Df(c)v[/tex].
[quote="mini"]ja imam pitanje vezano za taylorov teorem, tj kadtreba izracunati ostatak. npr zadatak s drugog kolokvija: f(x,y)=e^(xy)+x^2+y. izracunat taylorov polinom 1. stupnja u (1,2) i izracunat ostatak. [/quote]
[dtex]f(x,y)=e^2+5+(2e^2+2)(x-1)+(e^2+1)(y-2)+R(x,y)[/dtex]
gdje je
[dtex]R(x,y)=\frac{1}{2}((c_2^2e^{c_1c_2}+2)(x-1)^2+2(1+c_1c_2)e^{c_1c_2}(x-1)(y-2)+c_1^2e^{c_1c_2}(y-2)^2)[/dtex]
za neku točku [tex]c=(c_1,c_2)\in<(1,2),(x,y)>[/tex] .
Možda sam fuljala negdje u računu, ali ideja je samo slijediti formulu u kojoj piše opći oblik ostatka i u nju uvrstiti konkretne izraze za parcijalne derivacije drugog reda.
S druge strane, ostatak bi se mogao i eksplicitno izračunati kao [tex]f(x,y)-T(x,y)[/tex] (to je zapravo definicija ostatka), ali mislim da se nije htjelo da to napišete - to je nekako pretrivijalno; u svakom slučaju, ako niste sigurni, napišite i to.
Još mi je tjedan dana posao da vas spašavam. 
Da, kad vas se takve stvari pitaju na kolokviju, nije dovoljno samo napisati "očito je", posebno ako se negdje spominje "obrazložite sve tvrdnje" ili, još gore, "sve tvrdnje dokažite". Za ovaj bi kružni vijenac recimo bilo OK napisati da je ograničen jer je sadržan u kugli K(0, 3); za zatvorenost je, ako se ne traži 100%-tni dokaz, dovoljno skicirati skup i onda reći da je sa slike očito da za svaku točku komplementa postoji neka otvorena kugla sa središtem u njoj koja je sadržana u komplementu (možda na skici nacrtati tu kuglu za par točaka, da se vidi da je tebi to 100% jasno), što znači da je komplement otvoren pa je skup po definiciji zatvoren; ovo ipak još uvijek nije dovoljno ako se traži precizan dokaz - trebalo bi sve raspisati.
Preciznije bi bilo npr. promatrati proizvoljan niz [tex](x_k,y_k)[/tex] u tom skupu koji konvergira u [tex]\mathbb{R}^2[/tex] prema [tex](x,y)[/tex]. Onda vrijedi [tex]1\leq x_k^2+y_k^2\leq 4[/tex] pa, kad pustimo limes na tu nejednakost, iskoristivši da koordinatni nizovi konvergiraju prema x i y, imamo [tex]1\leq x^2+y^2\leq 4[/tex], pa je [tex](x,y)[/tex] u kružnom vijencu i po karakterizaciji zatvorenosti pomoću limesa imamo da je skup zatvoren.
Ili, najelegantnije, uočiti da je taj kružni vijenac zapravo [tex]f([1,2]\times[0,2\pi])[/tex] za fju [tex]f(r,\phi)=(r\cos\phi, r\sin\phi)[/tex] (polarne koordinate), dakle slika zatvorenog pravokutnika, za koji i ptice na grani znaju da je kompaktan, po neprekidnoj fji f, pa je kompaktan. Polarne koordinate mogu se lijepo iskoristiti za takve stvari uvijek kad imamo nekakve kružne skupove.
Sigurno ima još načina. Što je dokaz precizniji, to bolje.
Za povezanost opet možemo iskoristiti gornju fju f jer neprekidna fja povezane skupove (npr. pravokutnike) nosi u povezane, a pravokutnik je povezan jer je povezan putovima (npr. svake dvije točke povezuje put koji prođe po segmentu od jedne do druge).
Ili direktno pokažemo da je kružni vijenac povezan putovima - npr. za bilo koje dvije točke uočimo da se nalaze na koncentričnim kružnicama sa središtem u ishodištu, a put bismo onda mogli konstruirati tako da prvo iz jedne točke, u smjeru radijvektora te točke, prijeđe na kružnicu na kojoj je druga točka, a onda po toj kružnici doputuje do druge točke. Valjda bi se dale napisati i neke precizne jednadžbe, ali i ideje se cijene... 
To je glavni dio posla. Ako i ne znaš precizan dokaz, bar u jednoj rečenici obrazloži zašto je to tebi jasno.
http://web.math.pmf.unizg.hr/nastava/difraf/dif/2009-10-kol1/kol1_0910.pdf
6. a) Koordinatne fje su neprekidne jer su to linearne kombinacije nekih projekcija blablabla...
b) [tex]d(f(x_1,x_2,x_3),f(y_1,y_2,y_3))[/tex]
[tex]=||(x_1-x_3,x_1+x_2)-(y_1-y_3, y_1+y_2)||[/tex]
[tex]=||(x_1-y_1,0)+(-x_3+y_3,0)+(0,x_1-y_1)+(0,x_2-y_2)||[/tex]
[tex]\leq||(x_1-y_1,0)||+||(-x_3+y_3,0)||+||(0,x_1-y_1)||+||(0,x_2-y_2)||[/tex]
[tex]=|x_1-y_1|+|x_3-y_3|+|x_1-y_1|+|x_2-y_2|[/tex]
[tex]\leq4\sqrt{(x_1-y_1)^2+(x_2-y_2)^2+(x_3-y_3)^2}[/tex]
[tex]=4d((x_1,x_2,x_3),(y_1,y_2,y_3))[/tex]
pa ako za zadani [tex]\epsilon>0[/tex] uzmemo [tex]\delta=\frac{\epsilon}{4}[/tex], imamo uniformnu neprekidnost po definiciji.
Sa c) valjda nema problema, a onda za d) možemo iskoristiti [tex]\frac{\partial f}{\partial v}(c)=Df(c)v[/tex].
| mini (napisa): | | ja imam pitanje vezano za taylorov teorem, tj kadtreba izracunati ostatak. npr zadatak s drugog kolokvija: f(x,y)=e^(xy)+x^2+y. izracunat taylorov polinom 1. stupnja u (1,2) i izracunat ostatak. |
[dtex]f(x,y)=e^2+5+(2e^2+2)(x-1)+(e^2+1)(y-2)+R(x,y)[/dtex]
gdje je
[dtex]R(x,y)=\frac{1}{2}((c_2^2e^{c_1c_2}+2)(x-1)^2+2(1+c_1c_2)e^{c_1c_2}(x-1)(y-2)+c_1^2e^{c_1c_2}(y-2)^2)[/dtex]
za neku točku [tex]c=(c_1,c_2)\in<(1,2),(x,y)>[/tex] .
Možda sam fuljala negdje u računu, ali ideja je samo slijediti formulu u kojoj piše opći oblik ostatka i u nju uvrstiti konkretne izraze za parcijalne derivacije drugog reda.
S druge strane, ostatak bi se mogao i eksplicitno izračunati kao [tex]f(x,y)-T(x,y)[/tex] (to je zapravo definicija ostatka), ali mislim da se nije htjelo da to napišete - to je nekako pretrivijalno; u svakom slučaju, ako niste sigurni, napišite i to.
|
|
| [Vrh] |
|
markos
Forumaš(ica)
Pridružen/a: 20. 10. 2010. (20:09:26)
Postovi: (B)16
|
|
| [Vrh] |
|
googol
Forumaš(ica)


Pridružen/a: 29. 09. 2011. (21:23:09)
Postovi: (71)16
Spol: 
|
|
| [Vrh] |
|
mini
Forumaš(ica)
Pridružen/a: 04. 02. 2009. (14:31:34)
Postovi: (69)16
Spol: 
|
|
| [Vrh] |
|
sz
Forumaš(ica)


Pridružen/a: 26. 01. 2011. (15:17:39)
Postovi: (35)16
|
 Postano: 20:18 ned, 5. 2. 2012 Naslov: Postano: 20:18 ned, 5. 2. 2012 Naslov: |
    |
|
|
[quote="mini"]evo ja opet :)
popravni ispit 2008. 1.b) zad.
zbunjuje meovaj (Ax|x). napisala sam ga kao f1(x)x1 +...+fn(x)xn gdje su fi(x) i-ti redak matrice puta cijeli vektot x, al me zbunjuje kako sad to derivirat. moze li netko to sve malo ljepse raspisat? puno hvala[/quote]
Ma ne moraš se tu gnjaviti raspisivanjem, jednostavno uočiš da je fja [tex]g(x):=Ax[/tex] linearan operator, a linearni operatori su sami sebi diferencijali, tj. [tex]Dg(x)h=Ah[/tex] za svaki x. I sad za fju [tex]p(x)=(Ax|x)[/tex] samo upotrijebiš pravilo [tex]D(f_1|f_2)(x)h=(Df_1(x)h|f_2(x))+(f_1(x)|Df_2(x)h)[/tex] i dobiješ [tex]Dp(x)h=(Ah|x)+(Ax|h)[/tex], tj. [tex]Df(x)h=\frac{1}{2}((Ah|x)+(Ax|h))+(b|h)[/tex].
Ali ako baš hoćeš raspisivati sve parcijalne derivacije, prvi je korak [tex](Ax|x)=\sum_{i=1}^n\sum_{j=1}^na_{ij}x_ix_j[/tex].
| mini (napisa): | evo ja opet 
popravni ispit 2008. 1.b) zad.
zbunjuje meovaj (Ax|x). napisala sam ga kao f1(x)x1 +...+fn(x)xn gdje su fi(x) i-ti redak matrice puta cijeli vektot x, al me zbunjuje kako sad to derivirat. moze li netko to sve malo ljepse raspisat? puno hvala |
Ma ne moraš se tu gnjaviti raspisivanjem, jednostavno uočiš da je fja [tex]g(x):=Ax[/tex] linearan operator, a linearni operatori su sami sebi diferencijali, tj. [tex]Dg(x)h=Ah[/tex] za svaki x. I sad za fju [tex]p(x)=(Ax|x)[/tex] samo upotrijebiš pravilo [tex]D(f_1|f_2)(x)h=(Df_1(x)h|f_2(x))+(f_1(x)|Df_2(x)h)[/tex] i dobiješ [tex]Dp(x)h=(Ah|x)+(Ax|h)[/tex], tj. [tex]Df(x)h=\frac{1}{2}((Ah|x)+(Ax|h))+(b|h)[/tex].
Ali ako baš hoćeš raspisivati sve parcijalne derivacije, prvi je korak [tex](Ax|x)=\sum_{i=1}^n\sum_{j=1}^na_{ij}x_ix_j[/tex].
|
|
| [Vrh] |
|
|














