| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
dalmatinčica
Forumaš(ica)


Pridružen/a: 01. 10. 2011. (18:46:54)
Postovi: (AC)16
|
|
| [Vrh] |
|
pbakic
Forumaš(ica)

Pridružen/a: 05. 10. 2009. (17:48:30)
Postovi: (143)16
Spol: 
|
 Postano: 20:24 ned, 4. 3. 2012 Naslov: Postano: 20:24 ned, 4. 3. 2012 Naslov: |
    |
|
|
Ne treba previse raspisivati, dovoljno je gledati sto se tocno nalazi u jezgri operatora S:
[latex]p \in KerS [/latex] akko [latex] (t(p(t-2))''=0[/latex] (ova 0 je nulpolinom).
Druga derivacija nekog polinoma je nulpolinom akko je taj polinom stupnja manjeg ili jednakog 1.
Zakljucujemo da je stupanj polinoma tp(t-2) manji ili jednak 1, iz cega dobivamo stupanj od p=0. (p je konstanta)
Zakljucujemo da se jezgra od S sastoji od svih konstantnih polinoma, a sada je lakse pronaci odgovarajuce baze, rang i defekt...
(Ako treba jos malo raspisati, vici)
Ne treba previse raspisivati, dovoljno je gledati sto se tocno nalazi u jezgri operatora S:
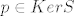 akko akko 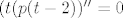 (ova 0 je nulpolinom). (ova 0 je nulpolinom).
Druga derivacija nekog polinoma je nulpolinom akko je taj polinom stupnja manjeg ili jednakog 1.
Zakljucujemo da je stupanj polinoma tp(t-2) manji ili jednak 1, iz cega dobivamo stupanj od p=0. (p je konstanta)
Zakljucujemo da se jezgra od S sastoji od svih konstantnih polinoma, a sada je lakse pronaci odgovarajuce baze, rang i defekt...
(Ako treba jos malo raspisati, vici)
|
|
| [Vrh] |
|
dalmatinčica
Forumaš(ica)


Pridružen/a: 01. 10. 2011. (18:46:54)
Postovi: (AC)16
|
|
| [Vrh] |
|
dalmatinčica
Forumaš(ica)


Pridružen/a: 01. 10. 2011. (18:46:54)
Postovi: (AC)16
|
|
| [Vrh] |
|
dalmatinčica
Forumaš(ica)


Pridružen/a: 01. 10. 2011. (18:46:54)
Postovi: (AC)16
|
|
| [Vrh] |
|
Shaman
Forumaš(ica)


Pridružen/a: 24. 09. 2011. (22:21:43)
Postovi: (76)16
Spol: 
|
|
| [Vrh] |
|
satja
Forumaš(ica)

Pridružen/a: 16. 05. 2010. (10:44:17)
Postovi: (F1)16
|
 Postano: 22:38 uto, 20. 3. 2012 Naslov: Postano: 22:38 uto, 20. 3. 2012 Naslov: |
    |
|
|
Neka je [tex]n = \dim V[/tex].
[b]Lema 1.[/b] [tex]r(A+I)+r(A-I) \le n[/tex].
Dokaz. [tex](A+I)(A-I) = A^2-AI+IA-I^2 = A^2 - A + A - I = 0[/tex], što znači [tex]Im(A-I)\subseteq Ker(A+I)[/tex] što daje [tex]r(A-I) \le n-r(A+I)[/tex].
[b]Lema 2.[/b] [tex]r(A+I)+r(A-I) \ge n[/tex].
Dokaz. Neka je [tex]\{b_1,\dots, b_n\}[/tex] baza za [tex]V[/tex] i neka je [tex]Ab_i = c_i[/tex]. Sada imamo [tex](A+I)b_i = c_i + b_i[/tex], kao i [tex](A-I)b_i = c_i - b_i[/tex]. Stoga, [dtex]r(A+I)=\dim [\{c_1+b_1,\dots,c_n+b_n\}], \quad r(A-I)=\dim [\{c_1-b_1,\dots,c_n-b_n\}].[/dtex] Označimo li gornje potprostore redom sa [tex]L[/tex] i [tex]M[/tex], imamo [dtex]r(A+I)+r(A-I)=\dim L + \dim M\ge \dim(L+M) = \dim [\{c_1+b_1, c_1-b_1,\dots,c_n+b_n, c_n-b_n\}].[/dtex] No posljednji je potprostor cijeli [tex]V[/tex], jer se bilo koji vektor iz baze [tex]b_i[/tex] može dobiti kao [tex]\frac 1 2(c_i+b_i) - \frac 1 2(c_i-b_i)[/tex], dakle vrijedi lema 2.
Ako treba neki korak bolje objasniti, javi se.
Neka je [tex]n = \dim V[/tex].
Lema 1. [tex]r(A+I)+r(A-I) \le n[/tex].
Dokaz. [tex](A+I)(A-I) = A^2-AI+IA-I^2 = A^2 - A + A - I = 0[/tex], što znači [tex]Im(A-I)\subseteq Ker(A+I)[/tex] što daje [tex]r(A-I) \le n-r(A+I)[/tex].
Lema 2. [tex]r(A+I)+r(A-I) \ge n[/tex].
Dokaz. Neka je [tex]\{b_1,\dots, b_n\}[/tex] baza za [tex]V[/tex] i neka je [tex]Ab_i = c_i[/tex]. Sada imamo [tex](A+I)b_i = c_i + b_i[/tex], kao i [tex](A-I)b_i = c_i - b_i[/tex]. Stoga, [dtex]r(A+I)=\dim [\{c_1+b_1,\dots,c_n+b_n\}], \quad r(A-I)=\dim [\{c_1-b_1,\dots,c_n-b_n\}].[/dtex] Označimo li gornje potprostore redom sa [tex]L[/tex] i [tex]M[/tex], imamo [dtex]r(A+I)+r(A-I)=\dim L + \dim M\ge \dim(L+M) = \dim [\{c_1+b_1, c_1-b_1,\dots,c_n+b_n, c_n-b_n\}].[/dtex] No posljednji je potprostor cijeli [tex]V[/tex], jer se bilo koji vektor iz baze [tex]b_i[/tex] može dobiti kao [tex]\frac 1 2(c_i+b_i) - \frac 1 2(c_i-b_i)[/tex], dakle vrijedi lema 2.
Ako treba neki korak bolje objasniti, javi se.
|
|
| [Vrh] |
|
dalmatinčica
Forumaš(ica)


Pridružen/a: 01. 10. 2011. (18:46:54)
Postovi: (AC)16
|
|
| [Vrh] |
|
dalmatinčica
Forumaš(ica)


Pridružen/a: 01. 10. 2011. (18:46:54)
Postovi: (AC)16
|
|
| [Vrh] |
|
Cobs
Forumaš(ica)


Pridružen/a: 21. 01. 2008. (13:32:15)
Postovi: (206)16
Spol: 
Lokacija: Geto
|
 Postano: 13:24 pet, 23. 3. 2012 Naslov: Postano: 13:24 pet, 23. 3. 2012 Naslov: |
    |
|
|
[quote="dalmatinčica"]http://web.math.pmf.unizg.hr/nastava/la/kolokviji/la2-0607-kol1a.pdf
može li uputa za 2. zadatak
kako da odredim sliku?[/quote]
sad kolko se sjećam to ne bi trebalo bit tak teško...
uzmeš jednu bazu v.p. polinoma ( stupnja manjeg ili jednakog n ), mislim da bi najjednostavnija bila:
[latex]\{ 1,t,t^2,\ldots , t^{n-1},t^n\}[/latex]
i pogledaš kak ovaj operator djeluje na bazu. Operator će ove polinome prebacivat u polinome, svi polinomi koje prebaci u nul polinom čine bazu za jezgru, ostali za sliku.
konkretno tebe zanima za koji od polinoma vrijedi...
[latex]\frac{p(t+a)-p(t)}{a} = 0[/latex]
da bi pronašli jezgru, tj. to je ekvivalentno sa
[latex]p(t+a)-p(t)=0[/latex]
a to je ekvivalentno sa:
[latex]p(t+a)=p(t)[/latex]
sad kad pogledaš bazu vektorskog prostora svih polinoma vidiš da je ovo vrijedi samo za polinom koji je konstanta...
[latex]1=1[/latex]
dok su ostali redom...
[latex]t+a=t[/latex]
[latex](t+a)^2=t^2[/latex]
itd. pa možeš zaključit da za ostale ne vrijedi jednakost.
Sad znaš bazu jezgre, znaš i koja je dimenzija jezgre i tu upotrijebiš tm. o rangu i defektu pa znaš odmah i dimenziju slike, pa znaš i sliku.
| dalmatinčica (napisa): | http://web.math.pmf.unizg.hr/nastava/la/kolokviji/la2-0607-kol1a.pdf
može li uputa za 2. zadatak
kako da odredim sliku? |
sad kolko se sjećam to ne bi trebalo bit tak teško...
uzmeš jednu bazu v.p. polinoma ( stupnja manjeg ili jednakog n ), mislim da bi najjednostavnija bila:
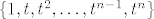
i pogledaš kak ovaj operator djeluje na bazu. Operator će ove polinome prebacivat u polinome, svi polinomi koje prebaci u nul polinom čine bazu za jezgru, ostali za sliku.
konkretno tebe zanima za koji od polinoma vrijedi...
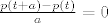
da bi pronašli jezgru, tj. to je ekvivalentno sa

a to je ekvivalentno sa:
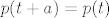
sad kad pogledaš bazu vektorskog prostora svih polinoma vidiš da je ovo vrijedi samo za polinom koji je konstanta...
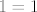
dok su ostali redom...
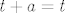
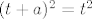
itd. pa možeš zaključit da za ostale ne vrijedi jednakost.
Sad znaš bazu jezgre, znaš i koja je dimenzija jezgre i tu upotrijebiš tm. o rangu i defektu pa znaš odmah i dimenziju slike, pa znaš i sliku.
|
|
| [Vrh] |
|
Cupcake
Forumaš(ica)

Pridružen/a: 01. 10. 2011. (18:52:00)
Postovi: (1B)16
Spol: 
|
|
| [Vrh] |
|
dalmatinčica
Forumaš(ica)


Pridružen/a: 01. 10. 2011. (18:46:54)
Postovi: (AC)16
|
 Postano: 20:21 uto, 27. 3. 2012 Naslov: Postano: 20:21 uto, 27. 3. 2012 Naslov: |
    |
|
|
[quote="Cobs"][quote="dalmatinčica"]http://web.math.pmf.unizg.hr/nastava/la/kolokviji/la2-0607-kol1a.pdf
može li uputa za 2. zadatak
kako da odredim sliku?[/quote]
sad kolko se sjećam to ne bi trebalo bit tak teško...
uzmeš jednu bazu v.p. polinoma ( stupnja manjeg ili jednakog n ), mislim da bi najjednostavnija bila:
[latex]\{ 1,t,t^2,\ldots , t^{n-1},t^n\}[/latex]
i pogledaš kak ovaj operator djeluje na bazu. Operator će ove polinome prebacivat u polinome, svi polinomi koje prebaci u nul polinom čine bazu za jezgru, ostali za sliku.
konkretno tebe zanima za koji od polinoma vrijedi...
[latex]\frac{p(t+a)-p(t)}{a} = 0[/latex]
da bi pronašli jezgru, tj. to je ekvivalentno sa
[latex]p(t+a)-p(t)=0[/latex]
a to je ekvivalentno sa:
[latex]p(t+a)=p(t)[/latex]
sad kad pogledaš bazu vektorskog prostora svih polinoma vidiš da je ovo vrijedi samo za polinom koji je konstanta...
[latex]1=1[/latex]
dok su ostali redom...
[latex]t+a=t[/latex]
[latex](t+a)^2=t^2[/latex]
itd. pa možeš zaključit da za ostale ne vrijedi jednakost.
Sad znaš bazu jezgre, znaš i koja je dimenzija jezgre i tu upotrijebiš tm. o rangu i defektu pa znaš odmah i dimenziju slike, pa znaš i sliku.[/quote]
znači baza za sliku je {t^(n-1), t^(n-2),...,t,1}??
| Cobs (napisa): | | dalmatinčica (napisa): | http://web.math.pmf.unizg.hr/nastava/la/kolokviji/la2-0607-kol1a.pdf
može li uputa za 2. zadatak
kako da odredim sliku? |
sad kolko se sjećam to ne bi trebalo bit tak teško...
uzmeš jednu bazu v.p. polinoma ( stupnja manjeg ili jednakog n ), mislim da bi najjednostavnija bila:
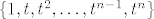
i pogledaš kak ovaj operator djeluje na bazu. Operator će ove polinome prebacivat u polinome, svi polinomi koje prebaci u nul polinom čine bazu za jezgru, ostali za sliku.
konkretno tebe zanima za koji od polinoma vrijedi...
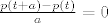
da bi pronašli jezgru, tj. to je ekvivalentno sa

a to je ekvivalentno sa:
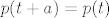
sad kad pogledaš bazu vektorskog prostora svih polinoma vidiš da je ovo vrijedi samo za polinom koji je konstanta...
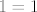
dok su ostali redom...
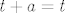
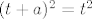
itd. pa možeš zaključit da za ostale ne vrijedi jednakost.
Sad znaš bazu jezgre, znaš i koja je dimenzija jezgre i tu upotrijebiš tm. o rangu i defektu pa znaš odmah i dimenziju slike, pa znaš i sliku. |
znači baza za sliku je {t^(n-1), t^(n-2),...,t,1}??
|
|
| [Vrh] |
|
satja
Forumaš(ica)

Pridružen/a: 16. 05. 2010. (10:44:17)
Postovi: (F1)16
|
 Postano: 23:14 uto, 27. 3. 2012 Naslov: Postano: 23:14 uto, 27. 3. 2012 Naslov: |
    |
|
|
[quote="Cobs"]i pogledaš kak ovaj operator djeluje na bazu. Operator će ove polinome prebacivat u polinome, svi polinomi koje prebaci u nul polinom čine bazu za jezgru, ostali za sliku.[/quote]
[b]To nije točno ni za jezgru ni za sliku![/b] (U ovom konkretnom zadatku je za jezgru točno, ali samo slučajno.)
Što se tiče kanonske baze vektorskog prostora, točno je da od vektora [tex]\{1, t, t^2, \dots, t^n\}[/tex] samo konstanta [tex]1[/tex] pripada jezgri operatora. Ali to još uvijek ne znači da je dimenzija jezgre jednaka [tex]1[/tex], jer u jezgri teoretski može biti i neka linearna kombinacija preostalih vektora kanonske baze.
Na primjer, kad bismo u vektorskom prostoru [tex]R^2[/tex] uzeli kanonsku bazu [tex]\{(1,0), (0,1)\}[/tex] te linearni operator [tex]L(x,y) = (x-y, 0)[/tex], lako je vidjeti da nijedan vektor kanonske baze nije u jezgri. Znači li to da je dimenzija jezgre jednaka [tex]0[/tex]? Ne, jer je baza za jezgru npr. vektor [tex](1,1)[/tex] koji ne pripada kanonskoj bazi.
Nije dakle dovoljno promatrati samo kanonsku bazu da bismo našli jezgru. U ovom slučaju ipak su u jezgri samo konstantni polinomi, jer [tex]p(t+a)=p(t)[/tex] za svaki [tex]t[/tex] ne može vrijediti za polinom stupnja većeg od [tex]0[/tex] (npr. zato jer takvi polinomi teže u [tex]\pm \infty[/tex] kad [tex]t \to \infty[/tex], a ovdje imamo [tex]p(t) = p(t+ka)[/tex] za svaki cijeli broj [tex]k[/tex]). Dimenzija jezgre je dakle [tex]1[/tex] pa je dimenzija slike [tex]n[/tex].
Sliku ne možemo znati odmah iz njezine dimenzije. (Znate li koliko ima vektorskih potprostora dimenzije [tex]n[/tex] unutar vektorskog prostora dimenzije [tex]n+1[/tex]? Beskonačno mnogo!) U našem slučaju valja primijetiti da se djelovanjem operatora [tex]D_a[/tex] vodeći koeficijent polinoma uvijek poništi, pa slika ne sadrži polinome stupnja [tex]n[/tex] - drugim riječima, slika je potprostor vektorskog prostora [tex]P_{n-1}[/tex]. No, ako potprostor ima istu dimenziju kao i vektorski prostor koji mu je nadskup, onda se oni podudaraju (dokažite za vježbu). Baza za sliku je dakle [tex]\{1, t, t^2, \dots, t^{n-1}\}[/tex].
| Cobs (napisa): | | i pogledaš kak ovaj operator djeluje na bazu. Operator će ove polinome prebacivat u polinome, svi polinomi koje prebaci u nul polinom čine bazu za jezgru, ostali za sliku. |
To nije točno ni za jezgru ni za sliku! (U ovom konkretnom zadatku je za jezgru točno, ali samo slučajno.)
Što se tiče kanonske baze vektorskog prostora, točno je da od vektora [tex]\{1, t, t^2, \dots, t^n\}[/tex] samo konstanta [tex]1[/tex] pripada jezgri operatora. Ali to još uvijek ne znači da je dimenzija jezgre jednaka [tex]1[/tex], jer u jezgri teoretski može biti i neka linearna kombinacija preostalih vektora kanonske baze.
Na primjer, kad bismo u vektorskom prostoru [tex]R^2[/tex] uzeli kanonsku bazu [tex]\{(1,0), (0,1)\}[/tex] te linearni operator [tex]L(x,y) = (x-y, 0)[/tex], lako je vidjeti da nijedan vektor kanonske baze nije u jezgri. Znači li to da je dimenzija jezgre jednaka [tex]0[/tex]? Ne, jer je baza za jezgru npr. vektor [tex](1,1)[/tex] koji ne pripada kanonskoj bazi.
Nije dakle dovoljno promatrati samo kanonsku bazu da bismo našli jezgru. U ovom slučaju ipak su u jezgri samo konstantni polinomi, jer [tex]p(t+a)=p(t)[/tex] za svaki [tex]t[/tex] ne može vrijediti za polinom stupnja većeg od [tex]0[/tex] (npr. zato jer takvi polinomi teže u [tex]\pm \infty[/tex] kad [tex]t \to \infty[/tex], a ovdje imamo [tex]p(t) = p(t+ka)[/tex] za svaki cijeli broj [tex]k[/tex]). Dimenzija jezgre je dakle [tex]1[/tex] pa je dimenzija slike [tex]n[/tex].
Sliku ne možemo znati odmah iz njezine dimenzije. (Znate li koliko ima vektorskih potprostora dimenzije [tex]n[/tex] unutar vektorskog prostora dimenzije [tex]n+1[/tex]? Beskonačno mnogo!) U našem slučaju valja primijetiti da se djelovanjem operatora [tex]D_a[/tex] vodeći koeficijent polinoma uvijek poništi, pa slika ne sadrži polinome stupnja [tex]n[/tex] - drugim riječima, slika je potprostor vektorskog prostora [tex]P_{n-1}[/tex]. No, ako potprostor ima istu dimenziju kao i vektorski prostor koji mu je nadskup, onda se oni podudaraju (dokažite za vježbu). Baza za sliku je dakle [tex]\{1, t, t^2, \dots, t^{n-1}\}[/tex].
|
|
| [Vrh] |
|
satja
Forumaš(ica)

Pridružen/a: 16. 05. 2010. (10:44:17)
Postovi: (F1)16
|
|
| [Vrh] |
|
dalmatinčica
Forumaš(ica)


Pridružen/a: 01. 10. 2011. (18:46:54)
Postovi: (AC)16
|
|
| [Vrh] |
|
kiara
Forumaš(ica)

Pridružen/a: 15. 11. 2011. (23:22:57)
Postovi: (55)16
|
|
| [Vrh] |
|
quark
Forumaš(ica)


Pridružen/a: 22. 10. 2011. (16:47:39)
Postovi: (DA)16
Spol: 
|
 Postano: 0:19 pet, 6. 4. 2012 Naslov: Postano: 0:19 pet, 6. 4. 2012 Naslov: |
    |
|
|
[quote="kiara"]Moze li mi netko pomoci s trecim zadatkom proslogodisnjeg prvog kolokvija?Pokusavam ga stalno rjesiti,ali vrtim se cijelo vrijeme oko 2 jednadzbe s 4 nepoznanice i nikako ne mogu odrediti vektore u bazi koja se trazi.Kako se to rjesi?[/quote]
Prikažeš operator u kanonskoj bazi i onda koristiš prijelazne matrice i svojstvo : [tex]I(e,f)=I(f,e)^{-1}[/tex]
[tex]I(f,e)A(e)I(e,f)=A(f)[/tex]
Pomnožimo zdesna s [tex]I(f,e)[/tex]:
[tex]I(f,e)A(e)=A(f)I(f,e)[/tex]
Dobijemo na kraju dvije jednadžbe s 4 nepoznanice; dakle, ima beskonačno mnogo takvih bazi (nigdje nije rečeno da svaka baza daje jedinstveni prikaz operatora). Odabereš dva vektora i gotovo :)
| kiara (napisa): | | Moze li mi netko pomoci s trecim zadatkom proslogodisnjeg prvog kolokvija?Pokusavam ga stalno rjesiti,ali vrtim se cijelo vrijeme oko 2 jednadzbe s 4 nepoznanice i nikako ne mogu odrediti vektore u bazi koja se trazi.Kako se to rjesi? |
Prikažeš operator u kanonskoj bazi i onda koristiš prijelazne matrice i svojstvo : [tex]I(e,f)=I(f,e)^{-1}[/tex]
[tex]I(f,e)A(e)I(e,f)=A(f)[/tex]
Pomnožimo zdesna s [tex]I(f,e)[/tex]:
[tex]I(f,e)A(e)=A(f)I(f,e)[/tex]
Dobijemo na kraju dvije jednadžbe s 4 nepoznanice; dakle, ima beskonačno mnogo takvih bazi (nigdje nije rečeno da svaka baza daje jedinstveni prikaz operatora). Odabereš dva vektora i gotovo 
|
|
| [Vrh] |
|
pedro
Forumaš(ica)

Pridružen/a: 21. 10. 2010. (14:08:21)
Postovi: (19B)16
|
|
| [Vrh] |
|
gflegar
Forumaš(ica)


Pridružen/a: 12. 10. 2011. (15:03:41)
Postovi: (10D)16
Spol: 
|
|
| [Vrh] |
|
thepineapple
Forumaš(ica)

Pridružen/a: 03. 11. 2011. (18:58:15)
Postovi: (12)16
|
|
| [Vrh] |
|
|










