| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
Lepi91
Forumaš(ica)


Pridružen/a: 15. 09. 2010. (15:22:23)
Postovi: (C8)16
Spol: 
|
|
| [Vrh] |
|
Joker
Forumaš(ica)

Pridružen/a: 19. 09. 2010. (10:19:16)
Postovi: (8C)16
Spol: 
|
|
| [Vrh] |
|
dalmatinčica
Forumaš(ica)


Pridružen/a: 01. 10. 2011. (18:46:54)
Postovi: (AC)16
|
|
| [Vrh] |
|
goranm
Forumaš(ica)


Pridružen/a: 12. 11. 2002. (20:09:12)
Postovi: (906)16
Spol: 
|
|
| [Vrh] |
|
dalmatinčica
Forumaš(ica)


Pridružen/a: 01. 10. 2011. (18:46:54)
Postovi: (AC)16
|
|
| [Vrh] |
|
goranm
Forumaš(ica)


Pridružen/a: 12. 11. 2002. (20:09:12)
Postovi: (906)16
Spol: 
|
 Postano: 23:07 pon, 12. 3. 2012 Naslov: Postano: 23:07 pon, 12. 3. 2012 Naslov: |
    |
|
|
Prvo provjeravamo za koje [latex]\alpha[/latex] je funkcija f dobro definirana. Diskriminanta jednadžbe [latex]x^2-x+\alpha=0[/latex] je [latex]1-4\alpha[/latex]. U ovisnosti o parametru [tex]\alpha[/tex] ta jednadžba imati će
1) jednu nultočku i u njoj [latex]\ln{(x^2-x+\alpha)}[/latex] neće biti definiran pa čitava funkcija neće biti definirana na R,
2) dvije nultočke pa funkcija neće biti definirana na nekom intervalu,
3) niti jednu nultočku, tj. [latex]x^2-x+\alpha[/latex] će biti pozitivan broj za svaki x iz R.
Prvi slučaj je za [latex]\alpha=\frac14[/latex]. Tada je [latex]x^2-x+\frac14=0 \iff x=\frac12[/latex] pa funkcija f nije uopće definirana na R pa ne može biti niti derivabilna na R.
Drugi slučaj je za [latex]\alpha<\frac14[/latex], tj. [latex]-\frac14+\alpha<0[/latex]. Tada je [latex]f(\frac12)=\ln{(-\frac14+\alpha)}[/latex] pa opet čitava funkcija nije definirana na R pa ne može biti niti derivabilna na R.
Treći slučaj je za [latex]\alpha>\frac14[/latex]. Tu je funkcija dobro definirana na R. Prvo treba naći [latex]\alpha[/latex] td. je f neprekidna na R. Očito je [latex]e^{1/x}-\beta x[/latex] neprekidna za svaki x<0 (jer je suma neprekidnih funkcija). Slično, [latex]\ln{(x^2-x+\alpha)}[/latex] je neprekidna za svaki x>0. Prema tome, f je neprekidna na R\{0}.
Ostaje još naći [latex]\alpha[/latex] td. f bude neprekidna u x=0. Dakle, mora biti [latex]\lim_{\limits{x\to0^+}}(\ln{(x^2-x+\alpha)})=\lim_{\limits{x\to0^-}}(e^{1/x}-\beta x)[/latex], odnosno [latex]\ln{\alpha}=0[/latex], tj. [latex]\alpha=1[/latex].
Ostaje još vidjeti kada će f biti derivabilna u 0, tj. za koji [latex]\beta[/latex] vrijedi
[tex]\lim_{x\to 0^-}\frac{f(x)-f(0)}{x-0}=\lim_{x\to 0^+}\frac{f(x)-f(0)}{x-0},[/tex]
što, kada se uvrsti f(x) i f(0) ispada
[tex]\lim_{x\to 0^-}\frac{e^{1/x}-\beta x}{x}=\lim_{x\to 0^+}\frac{\ln{(x^2-x+1)}}{x}.[/tex]
To ostavljam tebi da izračunaš. :)
Prvo provjeravamo za koje  je funkcija f dobro definirana. Diskriminanta jednadžbe je funkcija f dobro definirana. Diskriminanta jednadžbe  je je 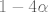 . U ovisnosti o parametru [tex]\alpha[/tex] ta jednadžba imati će . U ovisnosti o parametru [tex]\alpha[/tex] ta jednadžba imati će
1) jednu nultočku i u njoj  neće biti definiran pa čitava funkcija neće biti definirana na R, neće biti definiran pa čitava funkcija neće biti definirana na R,
2) dvije nultočke pa funkcija neće biti definirana na nekom intervalu,
3) niti jednu nultočku, tj. 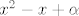 će biti pozitivan broj za svaki x iz R. će biti pozitivan broj za svaki x iz R.
Prvi slučaj je za  . Tada je . Tada je 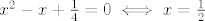 pa funkcija f nije uopće definirana na R pa ne može biti niti derivabilna na R. pa funkcija f nije uopće definirana na R pa ne može biti niti derivabilna na R.
Drugi slučaj je za 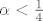 , tj. , tj. 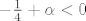 . Tada je . Tada je 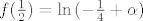 pa opet čitava funkcija nije definirana na R pa ne može biti niti derivabilna na R. pa opet čitava funkcija nije definirana na R pa ne može biti niti derivabilna na R.
Treći slučaj je za  . Tu je funkcija dobro definirana na R. Prvo treba naći . Tu je funkcija dobro definirana na R. Prvo treba naći  td. je f neprekidna na R. Očito je td. je f neprekidna na R. Očito je 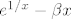 neprekidna za svaki x<0 (jer je suma neprekidnih funkcija). Slično, neprekidna za svaki x<0 (jer je suma neprekidnih funkcija). Slično,  je neprekidna za svaki x>0. Prema tome, f je neprekidna na R\{0}. je neprekidna za svaki x>0. Prema tome, f je neprekidna na R\{0}.
Ostaje još naći  td. f bude neprekidna u x=0. Dakle, mora biti td. f bude neprekidna u x=0. Dakle, mora biti 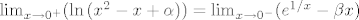 , odnosno , odnosno 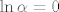 , tj. , tj. 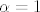 . .
Ostaje još vidjeti kada će f biti derivabilna u 0, tj. za koji 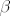 vrijedi vrijedi
[tex]\lim_{x\to 0^-}\frac{f(x)-f(0)}{x-0}=\lim_{x\to 0^+}\frac{f(x)-f(0)}{x-0},[/tex]
što, kada se uvrsti f(x) i f(0) ispada
[tex]\lim_{x\to 0^-}\frac{e^{1/x}-\beta x}{x}=\lim_{x\to 0^+}\frac{\ln{(x^2-x+1)}}{x}.[/tex]
To ostavljam tebi da izračunaš. 
_________________
The Dude Abides
|
|
| [Vrh] |
|
dalmatinčica
Forumaš(ica)


Pridružen/a: 01. 10. 2011. (18:46:54)
Postovi: (AC)16
|
|
| [Vrh] |
|
dalmatinčica
Forumaš(ica)


Pridružen/a: 01. 10. 2011. (18:46:54)
Postovi: (AC)16
|
|
| [Vrh] |
|
kenny
Petica iz zalaganja


Pridružen/a: 28. 03. 2003. (09:18:36)
Postovi: (3B7)16
Spol: 
Lokacija: ...somewhere over the rainbow...
|
|
| [Vrh] |
|
dalmatinčica
Forumaš(ica)


Pridružen/a: 01. 10. 2011. (18:46:54)
Postovi: (AC)16
|
|
| [Vrh] |
|
kenny
Petica iz zalaganja


Pridružen/a: 28. 03. 2003. (09:18:36)
Postovi: (3B7)16
Spol: 
Lokacija: ...somewhere over the rainbow...
|
|
| [Vrh] |
|
dalmatinčica
Forumaš(ica)


Pridružen/a: 01. 10. 2011. (18:46:54)
Postovi: (AC)16
|
|
| [Vrh] |
|
goranm
Forumaš(ica)


Pridružen/a: 12. 11. 2002. (20:09:12)
Postovi: (906)16
Spol: 
|
 Postano: 0:21 sri, 28. 3. 2012 Naslov: Postano: 0:21 sri, 28. 3. 2012 Naslov: |
    |
|
|
[quote="dalmatinčica"]kako da tu nađem lok ekstreme?
f´(x)=sinx+xcosx[/quote]
Kao i inače. Nađi nultočke prve derivacije, tj. f'(x)=0 akko sinx=-xcosx. Diskutiraj slučaj kada je cosx jednak nuli i kada je različit od nule. Kada je različit od nule, onda je tanx=-x.
Nacrtaj graf od tanx i od -x i zaključi u kojim intervalima se nalaze x-koordinate presjecišta tih grafova i gdje se te x-koordinate nalaze s obzirom na rubove tih intervala, tj. ako se x-koordinata presjecišta [latex](x_k,y_k)[/latex] nalazi u intervalu [latex]I_k=\left\langle k\pi-\frac\pi 2,k\pi+\frac\pi 2\right\rangle[/latex], onda se uvjeri da za dovoljno velike brojeve k vrijedi [latex]x_k\approx k\pi-\frac\pi 2[/latex] (iskoristi poznata svojstva funkcija -x i tanx da zaključiš da u svakom intervalu [latex]I_k[/latex] mora biti točno jedno presjecište).
Odmah da te upozorim, ne možeš egzaktno riješiti tanx=-x, ali s obzirom da trebaš nacrtati skicu, nije potrebno znati egzaktne vrijednosti na kojima se ekstremi nalaze, dovoljno je znati gdje se "otprilike" nalaze s obzirom na intervale [latex]I_k.[/latex]
| dalmatinčica (napisa): | kako da tu nađem lok ekstreme?
f´(x)=sinx+xcosx |
Kao i inače. Nađi nultočke prve derivacije, tj. f'(x)=0 akko sinx=-xcosx. Diskutiraj slučaj kada je cosx jednak nuli i kada je različit od nule. Kada je različit od nule, onda je tanx=-x.
Nacrtaj graf od tanx i od -x i zaključi u kojim intervalima se nalaze x-koordinate presjecišta tih grafova i gdje se te x-koordinate nalaze s obzirom na rubove tih intervala, tj. ako se x-koordinata presjecišta 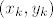 nalazi u intervalu nalazi u intervalu 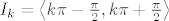 , onda se uvjeri da za dovoljno velike brojeve k vrijedi , onda se uvjeri da za dovoljno velike brojeve k vrijedi 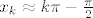 (iskoristi poznata svojstva funkcija -x i tanx da zaključiš da u svakom intervalu (iskoristi poznata svojstva funkcija -x i tanx da zaključiš da u svakom intervalu 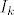 mora biti točno jedno presjecište). mora biti točno jedno presjecište).
Odmah da te upozorim, ne možeš egzaktno riješiti tanx=-x, ali s obzirom da trebaš nacrtati skicu, nije potrebno znati egzaktne vrijednosti na kojima se ekstremi nalaze, dovoljno je znati gdje se "otprilike" nalaze s obzirom na intervale 
_________________
The Dude Abides
|
|
| [Vrh] |
|
dalmatinčica
Forumaš(ica)


Pridružen/a: 01. 10. 2011. (18:46:54)
Postovi: (AC)16
|
|
| [Vrh] |
|
Phoenix
Forumaš(ica)


Pridružen/a: 15. 05. 2010. (18:46:07)
Postovi: (164)16
Sarma: -
|
|
| [Vrh] |
|
5_ra
Forumaš(ica)

Pridružen/a: 10. 12. 2011. (15:37:14)
Postovi: (28)16
|
|
| [Vrh] |
|
satja
Forumaš(ica)

Pridružen/a: 16. 05. 2010. (10:44:17)
Postovi: (F1)16
|
|
| [Vrh] |
|
5_ra
Forumaš(ica)

Pridružen/a: 10. 12. 2011. (15:37:14)
Postovi: (28)16
|
|
| [Vrh] |
|
Phoenix
Forumaš(ica)


Pridružen/a: 15. 05. 2010. (18:46:07)
Postovi: (164)16
Sarma: -
|
 Postano: 16:06 sub, 31. 3. 2012 Naslov: Postano: 16:06 sub, 31. 3. 2012 Naslov: |
    |
|
|
[quote="satja"]Ovo izgleda previše jednostavno, a znam da je neki zadatak za vrijeme kolokvija bio izmijenjen, pa slutim da je to taj. Možda se netko s druge godine sjeća kako je glasio "pravi" zadatak.[/quote]
Da, bio je izmijenjen. Al kako točno, ne znam, znam da se sve moralo raspisati da bi se odgovorila na oba pitanja. Možda je bilo [tex]f(x)=arctg(|x|^3)[/tex], ali to nije bila moja grupa.
Isto tako je moguće da je u drugoj grupi u prvom zadatku trebao ići [tex]arctg[/tex], a ne [tex]arcctg[/tex]. Premda je to bila moja grupa, ne sjećam se više...
| satja (napisa): | | Ovo izgleda previše jednostavno, a znam da je neki zadatak za vrijeme kolokvija bio izmijenjen, pa slutim da je to taj. Možda se netko s druge godine sjeća kako je glasio "pravi" zadatak. |
Da, bio je izmijenjen. Al kako točno, ne znam, znam da se sve moralo raspisati da bi se odgovorila na oba pitanja. Možda je bilo [tex]f(x)=arctg(|x|^3)[/tex], ali to nije bila moja grupa.
Isto tako je moguće da je u drugoj grupi u prvom zadatku trebao ići [tex]arctg[/tex], a ne [tex]arcctg[/tex]. Premda je to bila moja grupa, ne sjećam se više...
|
|
| [Vrh] |
|
marsupial
Forumaš(ica)

Pridružen/a: 09. 01. 2012. (22:46:33)
Postovi: (63)16
Spol: 
|
|
| [Vrh] |
|
|












