| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
Gost
|
|
| [Vrh] |
|
DsAg
Forumaš(ica)


Pridružen/a: 02. 10. 2005. (12:28:28)
Postovi: (17)16
Spol: 
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
DsAg
Forumaš(ica)


Pridružen/a: 02. 10. 2005. (12:28:28)
Postovi: (17)16
Spol: 
|
|
| [Vrh] |
|
Flame
Forumaš(ica)

Pridružen/a: 12. 08. 2009. (02:14:39)
Postovi: (53)16
Spol: 
|
 Postano: 23:28 pon, 9. 4. 2012 Naslov: Postano: 23:28 pon, 9. 4. 2012 Naslov: |
    |
|
|
@DsAg Svaka cast na trudu! Svidja mi se ideja iako sam trenutno preumoran da bih u detalje pregledao.
Ipak, ja bih preporucio Euler-Lagrangeove jednadzbe, buduci da smo u gravitacijskom polju, a jos je i gibanje jednodimenzionalno pa su i jednadzbe ustvari jednostavne.
Imamo dvije niti, pretpostavit cu nerastezljive. Oznacimo im duljine s [latex]c[/latex] i [latex]d[/latex]. Zatim redom oznacimo s [latex]x_1, x_2, x_3, y[/latex] udaljenosti masa [latex]m_i[/latex], odnosno "slobodne koloture" (koja se moze gibati, ali nema direktno na sebi masu) od "plafona".
Sada imamo veze [latex]2x_1-y=c,\; 2y+2x_2+2x_3=d[/latex] te pomocu toga postavimo sustav:
[latex]m_1\quad \ldots \quad x_1 = p, \; y = 2p-c \\
m_2\quad \ldots \quad x_2 = q \\
m_3\quad \ldots \quad x_3 = \frac{d}{2}-q-2p+c[/latex]
Nas zanimaju [latex]\ddot{p}[/latex] i [latex]\ddot{q} [/latex] pa izracunamo kineticku i potencijalnu energiju u terminima [latex]p[/latex] i [latex]q[/latex]. Sada samo trebamo postaviti Euler-Lagrangeove jednadzbe:
[latex]\frac{d}{dt}\left( \frac{\partial L}{\partial \dot{p}} \right) - \frac{\partial L}{\partial p} = 0 \\
\frac{d}{dt}\left( \frac{\partial L}{\partial \dot{q}} \right) - \frac{\partial L}{\partial q} = 0 \\[/latex]
Ja sam dobio sustav
[latex]
\begin{array}{lcr}
(m_1 + 4m_3) \ddot{p} + 2m_3 \ddot{q} & = & (m_1 - 2m_3)g \\
2m_3 \ddot{p} + (m_2 + m_3) \ddot{q} & = & (m_2 - m_3)g
\end{array}[/latex]
odakle lako dobivamo [latex]\ddot{x_1}, \ddot{x_2}, \ddot{x_3}[/latex].
Nadam se da je razumljivo i da nisam nesto fulao. :D
@DsAg Svaka cast na trudu! Svidja mi se ideja iako sam trenutno preumoran da bih u detalje pregledao.
Ipak, ja bih preporucio Euler-Lagrangeove jednadzbe, buduci da smo u gravitacijskom polju, a jos je i gibanje jednodimenzionalno pa su i jednadzbe ustvari jednostavne.
Imamo dvije niti, pretpostavit cu nerastezljive. Oznacimo im duljine s  i i 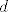 . Zatim redom oznacimo s . Zatim redom oznacimo s 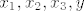 udaljenosti masa udaljenosti masa 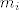 , odnosno "slobodne koloture" (koja se moze gibati, ali nema direktno na sebi masu) od "plafona". , odnosno "slobodne koloture" (koja se moze gibati, ali nema direktno na sebi masu) od "plafona".
Sada imamo veze 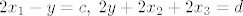 te pomocu toga postavimo sustav: te pomocu toga postavimo sustav:
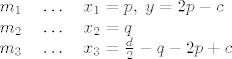
Nas zanimaju 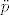 i i  pa izracunamo kineticku i potencijalnu energiju u terminima pa izracunamo kineticku i potencijalnu energiju u terminima  i i  . Sada samo trebamo postaviti Euler-Lagrangeove jednadzbe: . Sada samo trebamo postaviti Euler-Lagrangeove jednadzbe:
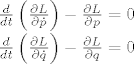
Ja sam dobio sustav
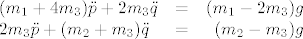
odakle lako dobivamo 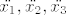 . .
Nadam se da je razumljivo i da nisam nesto fulao. 
|
|
| [Vrh] |
|
KG
Forumaš(ica)
Pridružen/a: 26. 01. 2011. (15:50:24)
Postovi: (30)16
Spol: 
|
|
| [Vrh] |
|
Flame
Forumaš(ica)

Pridružen/a: 12. 08. 2009. (02:14:39)
Postovi: (53)16
Spol: 
|
|
| [Vrh] |
|
KG
Forumaš(ica)

Pridružen/a: 26. 01. 2011. (15:50:24)
Postovi: (30)16
Spol: 
|
|
| [Vrh] |
|
Flame
Forumaš(ica)

Pridružen/a: 12. 08. 2009. (02:14:39)
Postovi: (53)16
Spol: 
|
|
| [Vrh] |
|
KG
Forumaš(ica)

Pridružen/a: 26. 01. 2011. (15:50:24)
Postovi: (30)16
Spol: 
|
|
| [Vrh] |
|
Flame
Forumaš(ica)

Pridružen/a: 12. 08. 2009. (02:14:39)
Postovi: (53)16
Spol: 
|
|
| [Vrh] |
|
DsAg
Forumaš(ica)


Pridružen/a: 02. 10. 2005. (12:28:28)
Postovi: (17)16
Spol: 
|
 Postano: 0:25 uto, 10. 4. 2012 Naslov: Postano: 0:25 uto, 10. 4. 2012 Naslov: |
    |
|
|
[quote="Flame"]@DsAg Svaka cast na trudu! Svidja mi se ideja iako sam trenutno preumoran da bih u detalje pregledao.
Ipak, ja bih preporucio Euler-Lagrangeove jednadzbe, buduci da smo u gravitacijskom polju, a jos je i gibanje jednodimenzionalno pa su i jednadzbe ustvari jednostavne.
Imamo dvije niti, pretpostavit cu nerastezljive. Oznacimo im duljine s [latex]c[/latex] i [latex]d[/latex]. Zatim redom oznacimo s [latex]x_1, x_2, x_3, y[/latex] udaljenosti masa [latex]m_i[/latex], odnosno "slobodne koloture" (koja se moze gibati, ali nema direktno na sebi masu) od "plafona".
Sada imamo veze [latex]2x_1-y=c,\; 2y+2x_2+2x_3=d[/latex] te pomocu toga postavimo sustav:
[latex]m_1\quad \ldots \quad x_1 = p, \; y = 2p-c \\
m_2\quad \ldots \quad x_2 = q \\
m_3\quad \ldots \quad x_3 = \frac{d}{2}-q-2p+c[/latex]
Nas zanimaju [latex]\ddot{p}[/latex] i [latex]\ddot{q} [/latex] pa izracunamo kineticku i potencijalnu energiju u terminima [latex]p[/latex] i [latex]q[/latex]. Sada samo trebamo postaviti Euler-Lagrangeove jednadzbe:
[latex]\frac{d}{dt}\left( \frac{\partial L}{\partial \dot{p}} \right) - \frac{\partial L}{\partial p} = 0 \\
\frac{d}{dt}\left( \frac{\partial L}{\partial \dot{q}} \right) - \frac{\partial L}{\partial q} = 0 \\[/latex]
Ja sam dobio sustav
[latex]
\begin{array}{lcr}
(m_1 + 4m_3) \ddot{p} + 2m_3 \ddot{q} & = & (m_1 - 2m_3)g \\
2m_3 \ddot{p} + (m_2 + m_3) \ddot{q} & = & (m_2 - m_3)g
\end{array}[/latex]
odakle lako dobivamo [latex]\ddot{x_1}, \ddot{x_2}, \ddot{x_3}[/latex].
Nadam se da je razumljivo i da nisam nesto fulao. :D[/quote]
Moze i tako. Meni je navika radit onak (cini mi se da su manje sanse da se fula kad je slozeniji problem).
Sretno svima na kolokviju!
Inace, generalno ak treba nekom pomoc il neko pojasnjenje oko statike, kinematike, mehanike fluida, termodinamike il tak neke primjenjene fizike, moze mi poslat i PM pa probam pomoc (cist da ne ceka da vidim post na forumu).
| Flame (napisa): | @DsAg Svaka cast na trudu! Svidja mi se ideja iako sam trenutno preumoran da bih u detalje pregledao.
Ipak, ja bih preporucio Euler-Lagrangeove jednadzbe, buduci da smo u gravitacijskom polju, a jos je i gibanje jednodimenzionalno pa su i jednadzbe ustvari jednostavne.
Imamo dvije niti, pretpostavit cu nerastezljive. Oznacimo im duljine s  i i 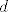 . Zatim redom oznacimo s . Zatim redom oznacimo s 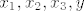 udaljenosti masa udaljenosti masa 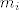 , odnosno "slobodne koloture" (koja se moze gibati, ali nema direktno na sebi masu) od "plafona". , odnosno "slobodne koloture" (koja se moze gibati, ali nema direktno na sebi masu) od "plafona".
Sada imamo veze 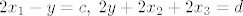 te pomocu toga postavimo sustav: te pomocu toga postavimo sustav:
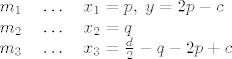
Nas zanimaju 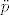 i i  pa izracunamo kineticku i potencijalnu energiju u terminima pa izracunamo kineticku i potencijalnu energiju u terminima  i i  . Sada samo trebamo postaviti Euler-Lagrangeove jednadzbe: . Sada samo trebamo postaviti Euler-Lagrangeove jednadzbe:
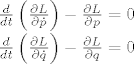
Ja sam dobio sustav
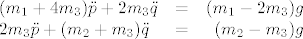
odakle lako dobivamo 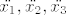 . .
Nadam se da je razumljivo i da nisam nesto fulao.  |
Moze i tako. Meni je navika radit onak (cini mi se da su manje sanse da se fula kad je slozeniji problem).
Sretno svima na kolokviju!
Inace, generalno ak treba nekom pomoc il neko pojasnjenje oko statike, kinematike, mehanike fluida, termodinamike il tak neke primjenjene fizike, moze mi poslat i PM pa probam pomoc (cist da ne ceka da vidim post na forumu).
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
|













