| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
Joker
Forumaš(ica)

Pridružen/a: 19. 09. 2010. (10:19:16)
Postovi: (8C)16
Spol: 
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
Borgcube
Forumaš(ica)
Pridružen/a: 01. 11. 2010. (21:14:10)
Postovi: (56)16
Lokacija: Tu i tamo.
|
|
| [Vrh] |
|
satja
Forumaš(ica)

Pridružen/a: 16. 05. 2010. (10:44:17)
Postovi: (F1)16
|
 Postano: 11:32 pon, 9. 4. 2012 Naslov: Postano: 11:32 pon, 9. 4. 2012 Naslov: |
    |
|
|
[quote="Anonymous"]Bi li mogao netko malo objasnit ovaj kompaktni zapis LU fakotorizacije?[/quote]
LU faktorizacija sastoji se od stvaranja gornjetrokutaste matrice U i donjetrokutaste matrice L. Gaussova eliminacija transformira polaznu matricu A tako da ona na koncu postane jednaka U. Ne treba dakle dodatno raditi matricu U za vrijeme Gaussove eliminacije, jer se matrica A prirodno u nju pretvara. Ni matricu L ne moramo posebno raditi, dovoljno je multiplikatore u Gaussovoj eliminaciji (od kojih se sastoji matrica L) upisivati na odgovarajuća mjesta matrice A, tamo gdje se "prava" matrica A pretvara u 0. Drugim riječima, pretvarajući k-ti stupac matrice A ispod dijagonale u 0, umjesto tih nula upisuješ multiplikatore koji čine matricu L (još im treba promijeniti predznak). Na koncu će u matrici A pisati matrice L i U: L u donjem, a U u gornjem dijelu. Zapis je kompaktan u smislu da ti ne trebaju tri, nego tek jedna matrica za čitav algoritam.
| Anonymous (napisa): | | Bi li mogao netko malo objasnit ovaj kompaktni zapis LU fakotorizacije? |
LU faktorizacija sastoji se od stvaranja gornjetrokutaste matrice U i donjetrokutaste matrice L. Gaussova eliminacija transformira polaznu matricu A tako da ona na koncu postane jednaka U. Ne treba dakle dodatno raditi matricu U za vrijeme Gaussove eliminacije, jer se matrica A prirodno u nju pretvara. Ni matricu L ne moramo posebno raditi, dovoljno je multiplikatore u Gaussovoj eliminaciji (od kojih se sastoji matrica L) upisivati na odgovarajuća mjesta matrice A, tamo gdje se "prava" matrica A pretvara u 0. Drugim riječima, pretvarajući k-ti stupac matrice A ispod dijagonale u 0, umjesto tih nula upisuješ multiplikatore koji čine matricu L (još im treba promijeniti predznak). Na koncu će u matrici A pisati matrice L i U: L u donjem, a U u gornjem dijelu. Zapis je kompaktan u smislu da ti ne trebaju tri, nego tek jedna matrica za čitav algoritam.
|
|
| [Vrh] |
|
ceps
Forumaš(ica)

Pridružen/a: 08. 10. 2010. (13:03:07)
Postovi: (13A)16
|
 Postano: 11:42 pon, 9. 4. 2012 Naslov: Postano: 11:42 pon, 9. 4. 2012 Naslov: |
    |
|
|
[quote="Anonymous"]Bi li mogao netko malo objasnit ovaj kompaktni zapis LU fakotorizacije?[/quote]
A što ti točno nije jasno s njim?
Kod LU faktorizacije rastavljamo matricu A na donjetrokutastu L i gornjetrokutastu U tako da vrijedi A = LU.
Matricu U dobivamo iz matrice A poništavanjem elemenata ispod glavne dijagonale (kao kod Gaussovih eliminacija), tako da je konačni rezultat nekako ovakav:
[latex]U = \begin{bmatrix}
a & b & c & d \\
0 & e & f & g \\
0 & 0 & h & i \\
0 & 0 & 0 & j \\
\end{bmatrix}[/latex]
Matrica L je donjetrokutasta i njezini elementi nam ''pokazuju'' s kojim brojevima smo množili pojedine retke u procesu pretvaranja matrice A u matricu U.
Ideja kompaktnog zapisa je:
- znamo da su u matrici U ispod dijagonale sve nule
- znamo da su elementi dijagonale kod L jedinice
Zato možemo zapisivati matrice L i U kompaktno, u jednoj matrici, ovako:
[latex] \begin{bmatrix}
u & u & u & u \\
l & u & u & u\\
l & l & u & u \\
l & l & l & u\\
\end{bmatrix}[/latex]
(Napomena: ovdje slova l i u samo pokazuju ''čiji je teritorij'', ne znači da svi ti brojevi moraju biti isti).
Znači u procesu poništavanja elemenata ispod dijagonale, usput si zapisuješ kako si ih poništio (s kojim si brojem množio koji redak da se elementi ponište).
Osim ljepšeg i kompaktnijeg zapisa, prednost je da je i permutiranje redaka lakše...
Mislim da nije teško shvatiti ovakav zapis ako dobro razumiješ LU rastav, budi siguran/sigurna da to prvo dobro kužiš.
EDIT: Vidim da sam malo zakasnio. :D
Al nek stoje obadva posta, duplo objašnjenje!
| Anonymous (napisa): | | Bi li mogao netko malo objasnit ovaj kompaktni zapis LU fakotorizacije? |
A što ti točno nije jasno s njim?
Kod LU faktorizacije rastavljamo matricu A na donjetrokutastu L i gornjetrokutastu U tako da vrijedi A = LU.
Matricu U dobivamo iz matrice A poništavanjem elemenata ispod glavne dijagonale (kao kod Gaussovih eliminacija), tako da je konačni rezultat nekako ovakav:
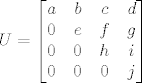
Matrica L je donjetrokutasta i njezini elementi nam ''pokazuju'' s kojim brojevima smo množili pojedine retke u procesu pretvaranja matrice A u matricu U.
Ideja kompaktnog zapisa je:
- znamo da su u matrici U ispod dijagonale sve nule
- znamo da su elementi dijagonale kod L jedinice
Zato možemo zapisivati matrice L i U kompaktno, u jednoj matrici, ovako:
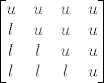
(Napomena: ovdje slova l i u samo pokazuju ''čiji je teritorij'', ne znači da svi ti brojevi moraju biti isti).
Znači u procesu poništavanja elemenata ispod dijagonale, usput si zapisuješ kako si ih poništio (s kojim si brojem množio koji redak da se elementi ponište).
Osim ljepšeg i kompaktnijeg zapisa, prednost je da je i permutiranje redaka lakše...
Mislim da nije teško shvatiti ovakav zapis ako dobro razumiješ LU rastav, budi siguran/sigurna da to prvo dobro kužiš.
EDIT: Vidim da sam malo zakasnio. 
Al nek stoje obadva posta, duplo objašnjenje!
Zadnja promjena: ceps; 11:46 pon, 9. 4. 2012; ukupno mijenjano 1 put.
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
satja
Forumaš(ica)

Pridružen/a: 16. 05. 2010. (10:44:17)
Postovi: (F1)16
|
 Postano: 12:02 pon, 9. 4. 2012 Naslov: Postano: 12:02 pon, 9. 4. 2012 Naslov: |
    |
|
|
[quote="Borgcube"]Čini mi se da se n-ovi pokrate pa je zapravo nevažno koji n uzmemo, ali nisam valjano raspisao to još :D[/quote]
Tako je. Želimo da su ocjene uniformne pogreške jednake, tj. da je [dtex]\frac 1 8 \cdot h_1^2 \cdot M_2(f|_{[0,2]}) =\frac 1 8 \cdot h_2^2 \cdot M_2(f|_{[2,c]}) \quad \Rightarrow \quad \bigg(\frac{2-0}{n}\bigg)^2\cdot |f''(0)| = \bigg(\frac{c-2}{n}\bigg)^2\cdot |f''(2)|. [/dtex] [tex]n[/tex] se pokrati i dobijemo [tex]c=4\sqrt 2+2[/tex].
| Borgcube (napisa): | Čini mi se da se n-ovi pokrate pa je zapravo nevažno koji n uzmemo, ali nisam valjano raspisao to još  |
Tako je. Želimo da su ocjene uniformne pogreške jednake, tj. da je [dtex]\frac 1 8 \cdot h_1^2 \cdot M_2(f|_{[0,2]}) =\frac 1 8 \cdot h_2^2 \cdot M_2(f|_{[2,c]}) \quad \Rightarrow \quad \bigg(\frac{2-0}{n}\bigg)^2\cdot |f''(0)| = \bigg(\frac{c-2}{n}\bigg)^2\cdot |f''(2)|. [/dtex] [tex]n[/tex] se pokrati i dobijemo [tex]c=4\sqrt 2+2[/tex].
Zadnja promjena: satja; 12:08 pon, 9. 4. 2012; ukupno mijenjano 2 put/a.
|
|
| [Vrh] |
|
zizu
Forumaš(ica)
Pridružen/a: 28. 03. 2010. (18:30:02)
Postovi: (A)16
|
|
| [Vrh] |
|
googol
Forumaš(ica)


Pridružen/a: 29. 09. 2011. (21:23:09)
Postovi: (71)16
Spol: 
|
 Postano: 13:59 pon, 9. 4. 2012 Naslov: Postano: 13:59 pon, 9. 4. 2012 Naslov: |
    |
|
|
[quote="satja"][quote="Borgcube"]Čini mi se da se n-ovi pokrate pa je zapravo nevažno koji n uzmemo, ali nisam valjano raspisao to još :D[/quote]
Tako je. Želimo da su ocjene uniformne pogreške jednake, tj. da je [dtex]\frac 1 8 \cdot h_1^2 \cdot M_2(f|_{[0,2]}) =\frac 1 8 \cdot h_2^2 \cdot M_2(f|_{[2,c]}) \quad \Rightarrow \quad \bigg(\frac{2-0}{n}\bigg)^2\cdot |f''(0)| = \bigg(\frac{c-2}{n}\bigg)^2\cdot |f''(2)|. [/dtex] [tex]n[/tex] se pokrati i dobijemo [tex]c=4\sqrt 2+2[/tex].[/quote]
Zar ne bi trebao gledati 2. derivaciju, a ne 1.?
| satja (napisa): | | Borgcube (napisa): | Čini mi se da se n-ovi pokrate pa je zapravo nevažno koji n uzmemo, ali nisam valjano raspisao to još  |
Tako je. Želimo da su ocjene uniformne pogreške jednake, tj. da je [dtex]\frac 1 8 \cdot h_1^2 \cdot M_2(f|_{[0,2]}) =\frac 1 8 \cdot h_2^2 \cdot M_2(f|_{[2,c]}) \quad \Rightarrow \quad \bigg(\frac{2-0}{n}\bigg)^2\cdot |f''(0)| = \bigg(\frac{c-2}{n}\bigg)^2\cdot |f''(2)|. [/dtex] [tex]n[/tex] se pokrati i dobijemo [tex]c=4\sqrt 2+2[/tex]. |
Zar ne bi trebao gledati 2. derivaciju, a ne 1.?
|
|
| [Vrh] |
|
satja
Forumaš(ica)

Pridružen/a: 16. 05. 2010. (10:44:17)
Postovi: (F1)16
|
|
| [Vrh] |
|
kosani
Forumaš(ica)
Pridružen/a: 14. 11. 2010. (21:22:58)
Postovi: (26)16
|
|
| [Vrh] |
|
googol
Forumaš(ica)


Pridružen/a: 29. 09. 2011. (21:23:09)
Postovi: (71)16
Spol: 
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
jabuka
Forumaš(ica)
Pridružen/a: 21. 11. 2009. (15:53:14)
Postovi: (7C)16
|
|
| [Vrh] |
|
satja
Forumaš(ica)

Pridružen/a: 16. 05. 2010. (10:44:17)
Postovi: (F1)16
|
|
| [Vrh] |
|
Phoenix
Forumaš(ica)


Pridružen/a: 15. 05. 2010. (18:46:07)
Postovi: (164)16
Sarma: -
|
 Postano: 16:23 pon, 9. 4. 2012 Naslov: Postano: 16:23 pon, 9. 4. 2012 Naslov: |
    |
|
|
Evo moje rješenje pa ako sam nešto zabrljao ili pogriješio, slobodno uputite. Nisam skroz siguran niti sam previše provjeravao, ali evo, za početak...
(Uglavnom ga pišem i da netko potvrdi ili opovrgne.)
(a) [tex]\frac{(\frac{1}{4}x^2)^k}{k!(k+1)!}=\frac{1}{16^kk!(k+1)!}[/tex]. Neka je [tex]n \in \mathbb{N}[/tex] takav da je [tex]\frac{1}{16^nn!(n+1)!}<\epsilon[/tex]. Grešku promatram kao ostatak reda, pa vrijedi: [tex]\sum_{k=n+1}^{\infty}\frac{1}{16^kk!(k+1)!}=\sum_{k=n+1}^{\infty}\frac{1}{16^nn!(n+1)!} \cdot \frac{1}{16^{k-n}(n+1) \cdots k \cdot (n+2) \cdots (k+1)}[/tex]
Prvi faktor ne ovisi o indeksu sume i manji je od [tex]\epsilon[/tex]. Za drugi, pak, vrijedi:
[tex]\frac{1}{16^{k-n+1}(n+1) \cdots (k+1) \cdot (n+2) \cdots (k+2)}=\frac{1}{16^{k-n}(n+1) \cdots k \cdot (n+2) \cdots (k+1)} \cdot \frac{1}{16(k+1)(k+2)}[/tex]
Dakle, svaki novi sumand nastaje množenjem prethodnog s [tex]\frac{1}{16k(k+1)}[/tex] (s tim da je početni sumand istog oblika). Uočimo: prvi sumand može biti najviše [tex]\frac{1}{16 \cdot 2(2+1)}=\frac{1}{96}<\frac{1}{2}[/tex] (za [tex]n=1[/tex] i [tex]k=n+1=2[/tex]). Iz ovoga općenito slijedi [tex]\frac{1}{16k(k+1)}<\frac{1}{2}[/tex], pa možemo zaključiti da gornju "sređenu" sumu možemo odozgo ograničiti s geometrijskim redom [tex]\sum_{k=1}^{\infty}\frac{1}{2^k}[/tex] čija je suma [tex]1[/tex]. Dakle, ostatak reda je odozgo ograničen s [tex]\epsilon[/tex], što je dobra ocjena pa će i aproksimacija biti približno točna.
(b) Sasvim slično, s tim da sam prvo zaključio da opći oblik izraza, dakle [tex]\frac{100^k}{k!(k+1)!}[/tex], raste kako [tex]k[/tex] raste do [tex]9[/tex], pa zatim pada. Dodatno sam zaključio (uz ovaj argument) da je ovaj razlomak manji od [tex]1[/tex] za [tex]k \geq 23[/tex]; to mi je pomoglo za donju granicu broja [tex]n[/tex] (kako bi opći element uopće mogao pasti ispod [tex]\epsilon[/tex]). I dalje na sličan način...
@jabuka: Uvrsti zadane uvjete u proizvoljan polinom [tex]p(x)=Ax^3+Bx^2+Cx+D[/tex]. Napravi ključnu matricu kojom ćeš prikazati dobiveni sustav četiriju jednadžbi s četiri nepoznanice. Rješenje postoji i jedinstveno je akko je matrica regularna akko je determinanta različita od nule.
Evo moje rješenje pa ako sam nešto zabrljao ili pogriješio, slobodno uputite. Nisam skroz siguran niti sam previše provjeravao, ali evo, za početak...
(Uglavnom ga pišem i da netko potvrdi ili opovrgne.)
(a) [tex]\frac{(\frac{1}{4}x^2)^k}{k!(k+1)!}=\frac{1}{16^kk!(k+1)!}[/tex]. Neka je [tex]n \in \mathbb{N}[/tex] takav da je [tex]\frac{1}{16^nn!(n+1)!}<\epsilon[/tex]. Grešku promatram kao ostatak reda, pa vrijedi: [tex]\sum_{k=n+1}^{\infty}\frac{1}{16^kk!(k+1)!}=\sum_{k=n+1}^{\infty}\frac{1}{16^nn!(n+1)!} \cdot \frac{1}{16^{k-n}(n+1) \cdots k \cdot (n+2) \cdots (k+1)}[/tex]
Prvi faktor ne ovisi o indeksu sume i manji je od [tex]\epsilon[/tex]. Za drugi, pak, vrijedi:
[tex]\frac{1}{16^{k-n+1}(n+1) \cdots (k+1) \cdot (n+2) \cdots (k+2)}=\frac{1}{16^{k-n}(n+1) \cdots k \cdot (n+2) \cdots (k+1)} \cdot \frac{1}{16(k+1)(k+2)}[/tex]
Dakle, svaki novi sumand nastaje množenjem prethodnog s [tex]\frac{1}{16k(k+1)}[/tex] (s tim da je početni sumand istog oblika). Uočimo: prvi sumand može biti najviše [tex]\frac{1}{16 \cdot 2(2+1)}=\frac{1}{96}<\frac{1}{2}[/tex] (za [tex]n=1[/tex] i [tex]k=n+1=2[/tex]). Iz ovoga općenito slijedi [tex]\frac{1}{16k(k+1)}<\frac{1}{2}[/tex], pa možemo zaključiti da gornju "sređenu" sumu možemo odozgo ograničiti s geometrijskim redom [tex]\sum_{k=1}^{\infty}\frac{1}{2^k}[/tex] čija je suma [tex]1[/tex]. Dakle, ostatak reda je odozgo ograničen s [tex]\epsilon[/tex], što je dobra ocjena pa će i aproksimacija biti približno točna.
(b) Sasvim slično, s tim da sam prvo zaključio da opći oblik izraza, dakle [tex]\frac{100^k}{k!(k+1)!}[/tex], raste kako [tex]k[/tex] raste do [tex]9[/tex], pa zatim pada. Dodatno sam zaključio (uz ovaj argument) da je ovaj razlomak manji od [tex]1[/tex] za [tex]k \geq 23[/tex]; to mi je pomoglo za donju granicu broja [tex]n[/tex] (kako bi opći element uopće mogao pasti ispod [tex]\epsilon[/tex]). I dalje na sličan način...
@jabuka: Uvrsti zadane uvjete u proizvoljan polinom [tex]p(x)=Ax^3+Bx^2+Cx+D[/tex]. Napravi ključnu matricu kojom ćeš prikazati dobiveni sustav četiriju jednadžbi s četiri nepoznanice. Rješenje postoji i jedinstveno je akko je matrica regularna akko je determinanta različita od nule.
|
|
| [Vrh] |
|
Gost
|
 Postano: 16:36 pon, 9. 4. 2012 Naslov: Postano: 16:36 pon, 9. 4. 2012 Naslov: |
    |
|
|
[quote="satja"][quote="Anonymous"]
Vidimo sam necije biljeske sa demonstratura i a) dio zadatka je rjesavan preko formule za ocijenu uniformne pogreske na ekvidistantnoj mreži. [/quote]
Da li misliš na treću formulu iz službenog šalabahtera? Ako da, to mi se čini prilično pogrešno, jer ta formula vrijedi za interpolacijski polinom, a u ovom zadatku ne aproksimiramo polinomom već po dijelovima linearnom funkcijom (koja na cijelom [a, b] nije polinom).[/quote]
da, na demonstraturama je rijesen tako da smo trazili n-tu derivaciju i koristili se tom trecom formulom. ((h)^n+1)/n+1 *M
Da li mozemo rijesiti pomocu formule za 1/8 * delta ^2 * M2(f) ?
| satja (napisa): | | Anonymous (napisa): |
Vidimo sam necije biljeske sa demonstratura i a) dio zadatka je rjesavan preko formule za ocijenu uniformne pogreske na ekvidistantnoj mreži. |
Da li misliš na treću formulu iz službenog šalabahtera? Ako da, to mi se čini prilično pogrešno, jer ta formula vrijedi za interpolacijski polinom, a u ovom zadatku ne aproksimiramo polinomom već po dijelovima linearnom funkcijom (koja na cijelom [a, b] nije polinom). |
da, na demonstraturama je rijesen tako da smo trazili n-tu derivaciju i koristili se tom trecom formulom. ((h)^n+1)/n+1 *M
Da li mozemo rijesiti pomocu formule za 1/8 * delta ^2 * M2(f) ?
|
|
| [Vrh] |
|
kosani
Forumaš(ica)
Pridružen/a: 14. 11. 2010. (21:22:58)
Postovi: (26)16
|
|
| [Vrh] |
|
|







