| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
mrvicaa
Forumaš(ica)

Pridružen/a: 26. 10. 2011. (22:00:15)
Postovi: (5)16
|
|
| [Vrh] |
|
dalmatinčica
Forumaš(ica)


Pridružen/a: 01. 10. 2011. (18:46:54)
Postovi: (AC)16
|
|
| [Vrh] |
|
Phoenix
Forumaš(ica)


Pridružen/a: 15. 05. 2010. (18:46:07)
Postovi: (164)16
Sarma: -
|
 Postano: 13:17 sub, 24. 3. 2012 Naslov: Postano: 13:17 sub, 24. 3. 2012 Naslov: |
    |
|
|
Dat ću ti samo hintove, ne bi bilo u redu da nekima pokvarimo užitak samostalnog rješavanja ovih zadataka. :P
Al dobro, bude li nejasno ili ti ne pomogne previše, kaži pa ćeš dobiti i nešto detaljnije rješenje (ili hint, štogod ti bude trebalo).
[quote="dalmatinčica"]evo kad su se napokon pojavili
http://web.math.pmf.unizg.hr/nastava/analiza/kolokviji/ma2-1011-pop.pdf
1. zad a i b
pogotovo b
hvala[/quote]
1. a) Što je po definiciji derivacija funkcije u nekoj točki? Posebno, što je derivacije funkcije u nuli? Probaj to primijeniti na već postojeće [tex]f(x)[/tex] koje imaš i u brojniku i u nazivniku i dobit ćeš rješenje.
b) Bilo koja derivacija od [tex]e^x[/tex] je [tex]e^x[/tex]. Međutim, proizvoljna derivacija od [tex]e^{x^3}[/tex] je [tex]e^{x^3}[/tex] puta "nešto". Što je to "nešto"? Probaj napraviti prvih nekoliko derivacija da uočiš što bi mogla dobiti za [tex]2011.[/tex] derivaciju. Sad kad imaš tu derivaciju i množiš [tex]e^{-x^3} \cdot e^{x^3} \cdot (nešto)[/tex], tražiš 4022. derivaciju "nečega". Kolika je ona?
[quote="dalmatinčica"]http://web.math.pmf.unizg.hr/nastava/analiza/kolokviji/ma2-1011-kol1.pdf
i ovdje
2. grupa 1. zadatak pod b)
f nije derivabilna bijekcija ili se varam?[/quote]
[strike]Varaš se. :) Po čemu si zaključila da nije? Napiši svoje rješenje pa da vidim (možeš i u inbox ako ne želiš ovdje).[/strike]
EDIT: Isprike, ipak se ja varam. Mislio sam da je u zadatku [tex]arctg[/tex]. :oops:
Dat ću ti samo hintove, ne bi bilo u redu da nekima pokvarimo užitak samostalnog rješavanja ovih zadataka. 
Al dobro, bude li nejasno ili ti ne pomogne previše, kaži pa ćeš dobiti i nešto detaljnije rješenje (ili hint, štogod ti bude trebalo).
1. a) Što je po definiciji derivacija funkcije u nekoj točki? Posebno, što je derivacije funkcije u nuli? Probaj to primijeniti na već postojeće [tex]f(x)[/tex] koje imaš i u brojniku i u nazivniku i dobit ćeš rješenje.
b) Bilo koja derivacija od [tex]e^x[/tex] je [tex]e^x[/tex]. Međutim, proizvoljna derivacija od [tex]e^{x^3}[/tex] je [tex]e^{x^3}[/tex] puta "nešto". Što je to "nešto"? Probaj napraviti prvih nekoliko derivacija da uočiš što bi mogla dobiti za [tex]2011.[/tex] derivaciju. Sad kad imaš tu derivaciju i množiš [tex]e^{-x^3} \cdot e^{x^3} \cdot (nešto)[/tex], tražiš 4022. derivaciju "nečega". Kolika je ona?
| dalmatinčica (napisa): | http://web.math.pmf.unizg.hr/nastava/analiza/kolokviji/ma2-1011-kol1.pdf
i ovdje
2. grupa 1. zadatak pod b)
f nije derivabilna bijekcija ili se varam? |
Varaš se.  Po čemu si zaključila da nije? Napiši svoje rješenje pa da vidim (možeš i u inbox ako ne želiš ovdje). Po čemu si zaključila da nije? Napiši svoje rješenje pa da vidim (možeš i u inbox ako ne želiš ovdje).
EDIT: Isprike, ipak se ja varam. Mislio sam da je u zadatku [tex]arctg[/tex]. 
|
|
| [Vrh] |
|
jema
Forumaš(ica)

Pridružen/a: 29. 09. 2011. (15:56:35)
Postovi: (52)16
|
|
| [Vrh] |
|
dalmatinčica
Forumaš(ica)


Pridružen/a: 01. 10. 2011. (18:46:54)
Postovi: (AC)16
|
|
| [Vrh] |
|
bubi1991
Forumaš(ica)

Pridružen/a: 22. 06. 2011. (11:50:16)
Postovi: (7)16
|
|
| [Vrh] |
|
Vishykc
Forumaš(ica)


Pridružen/a: 23. 10. 2010. (14:38:08)
Postovi: (6A)16
Spol: 
Lokacija: Zagreb
|
 Postano: 23:02 sub, 14. 4. 2012 Naslov: Postano: 23:02 sub, 14. 4. 2012 Naslov: |
    |
|
|
[quote="bubi1991"]kako dođemo do ovog limesa? --> http://www.wolframalpha.com/input/?i=lim_%28x-%3E0-%29%28-1%2Fx^2%29*e^%281%2Fx%29[/quote]
Uvrštavaš sve bliže brojeve 0 (upravo def. limesa, što se događa sa funkcijskim vrijednostima kad se x približava točki c, što je sada 0). Limes slijeva znači da su brojevi manji od 0. Probaš ovako: f(-0.1) = 10, f(-0.01) =100, f(-0.001) = 1000, očito je taj limes +[tex]\infty[/tex].
Edit: Znači, ovo vrijedi za funkciju [tex]f(x) = \frac{-1}{x}[/tex] jer nije cijeli link iskopiran pravilno u forum. Isprike za spam!
Uvrštavaš sve bliže brojeve 0 (upravo def. limesa, što se događa sa funkcijskim vrijednostima kad se x približava točki c, što je sada 0). Limes slijeva znači da su brojevi manji od 0. Probaš ovako: f(-0.1) = 10, f(-0.01) =100, f(-0.001) = 1000, očito je taj limes +[tex]\infty[/tex].
Edit: Znači, ovo vrijedi za funkciju [tex]f(x) = \frac{-1}{x}[/tex] jer nije cijeli link iskopiran pravilno u forum. Isprike za spam!
_________________
U matematici se sve smije, osim pogriješiti!
Zadnja promjena: Vishykc; 1:09 ned, 15. 4. 2012; ukupno mijenjano 1 put.
|
|
| [Vrh] |
|
quark
Forumaš(ica)


Pridružen/a: 22. 10. 2011. (16:47:39)
Postovi: (DA)16
Spol: 
|
 Postano: 23:50 sub, 14. 4. 2012 Naslov: Postano: 23:50 sub, 14. 4. 2012 Naslov: |
    |
|
|
[quote="Vishykc"][quote="bubi1991"]kako dođemo do ovog limesa? --> http://www.wolframalpha.com/input/?i=lim_%28x-%3E0-%29%28-1%2Fx^2%29*e^%281%2Fx%29[/quote]
Uvrštavaš sve bliže brojeve 0 (upravo def. limesa, što se događa sa funkcijskim vrijednostima kad se x približava točki c, što je sada 0). Limes slijeva znači da su brojevi manji od 0. Probaš ovako: f(-0.1) = 10, f(-0.01) =100, f(-0.001) = 1000, očito je taj limes +[tex]\infty[/tex].[/quote]
To može biti samo skica, ili eventualno provjera, ali nikako argumentacija.
(I limes nije [tex]+\infty[/tex], nego [tex]0[/tex], kao što i WA kaže; krivo računaš funkcijske vrijednosti :wink:)
Uvrsti supstituciju [tex]t=\frac{1}{x}[/tex], naštimaj da možeš koristiti L'H (više puta) i dobiješ limes :wink:
| Vishykc (napisa): |
Uvrštavaš sve bliže brojeve 0 (upravo def. limesa, što se događa sa funkcijskim vrijednostima kad se x približava točki c, što je sada 0). Limes slijeva znači da su brojevi manji od 0. Probaš ovako: f(-0.1) = 10, f(-0.01) =100, f(-0.001) = 1000, očito je taj limes +[tex]\infty[/tex]. |
To može biti samo skica, ili eventualno provjera, ali nikako argumentacija.
(I limes nije [tex]+\infty[/tex], nego [tex]0[/tex], kao što i WA kaže; krivo računaš funkcijske vrijednosti  ) )
Uvrsti supstituciju [tex]t=\frac{1}{x}[/tex], naštimaj da možeš koristiti L'H (više puta) i dobiješ limes 
|
|
| [Vrh] |
|
Vishykc
Forumaš(ica)


Pridružen/a: 23. 10. 2010. (14:38:08)
Postovi: (6A)16
Spol: 
Lokacija: Zagreb
|
|
| [Vrh] |
|
Zenon
Forumaš(ica)


Pridružen/a: 09. 09. 2011. (19:14:43)
Postovi: (2B1)16
Sarma: -
Lokacija: [tex]\pm\infty[/tex]
|
 Postano: 0:18 ned, 15. 4. 2012 Naslov: Postano: 0:18 ned, 15. 4. 2012 Naslov: |
    |
|
|
[quote="Vishykc"]Naravno da nije dokaz, ali to nije vjerojatno nije ni potrebno zasad(vjerojatno tok funkcije). A dobro ja uvrštavam, i limes je +[tex]\infty[/tex], kao što kaže WA :wink:[/quote]
Ne. Dobro je quark rekao. Ti si kliknuo na "link", a taj link nije potpun jer ga forum "prepolovi", a nisu svi korisnici naučili koristiti forum, niti ih to interesira. Ovo je pravi [url=http://www.wolframalpha.com/input/?i=lim_%28x-%3E0-%29%28-1%2Fx^2%29*e^%281%2Fx%29]link[/url].
| Vishykc (napisa): | Naravno da nije dokaz, ali to nije vjerojatno nije ni potrebno zasad(vjerojatno tok funkcije). A dobro ja uvrštavam, i limes je +[tex]\infty[/tex], kao što kaže WA  |
Ne. Dobro je quark rekao. Ti si kliknuo na "link", a taj link nije potpun jer ga forum "prepolovi", a nisu svi korisnici naučili koristiti forum, niti ih to interesira. Ovo je pravi link.
|
|
| [Vrh] |
|
quark
Forumaš(ica)


Pridružen/a: 22. 10. 2011. (16:47:39)
Postovi: (DA)16
Spol: 
|
 Postano: 0:55 ned, 15. 4. 2012 Naslov: Postano: 0:55 ned, 15. 4. 2012 Naslov: |
    |
|
|
[quote="dalmatinčica"]http://web.math.pmf.unizg.hr/nastava/analiza/kolokviji/ma2-1011-pop.pdf
kako riješiti 2. zadatak a i b
:oops:[/quote]
2. zadatak: a) funkcija je derivabilna samo u 0, a u ostalim nije niti neprekidna.
(Skiciraj si sliku i bit će ti jasno)
Dakle, treba dokazati da postoji [tex]\lim_{x->0}= \frac{f(x)-0}{x-0}[/tex]; sad, mi ne znamo koliko je [tex]f(x)[/tex], jer se k 0 mogu približavati i racionalni i iracionalni (oba su skupa gusta u R); ali kako se i za racionalne i iracionalne, kada x teži u 0, funkcijske vrijednosti približavaju 0 (samo s drugih strana), naslućujemo da je ipak derivabilna. "[strike]Uklještimo" izraz s najvećim mogućim slučajem, a to je kad je x iracionalan:[/strike]
edit:
[latex]0 \leq \frac{f(x)-f(0)}{x-0} \leq \left |\frac{\pm x^2}{x} \right | = |x|[/latex]
Po teoremu o sendviču, ovaj limes, za x->0, postoji (i jednak je 0).
Kako dokazati da nije derivabilna u svim ostalim točkama? Dovoljno je pokazati da nije neprekidna u tim točkama.
Uzmimo neki niz racionalnih brojeva [tex]a_n \mapsto c [/tex], [tex]c \neq 0[/tex] (to možemo jer je Q gust u R). Slijedi:
[tex]\lim_{n->\infty} f(a_n)=c^2[/tex]
Analogno, uzmemo niz iracionalnih brojeva [tex]b_n \mapsto c [/tex], [tex]c \neq 0[/tex]. Slijedi:
[tex]\lim_{n->\infty} f(b_n)=-c^2[/tex]
[tex]c^2 = - c^2 \Leftrightarrow c=0[/tex]
Kontradikcija.
b) Još bih malo razmislio; ovo za sada znam:
[latex]f(x)=\sum_{n=0}^{99}\frac{x^n}{n!}(e^{-x})[/latex]
[latex]f'(x)=\sum_{n=0}^{98}\frac{x^n}{n!}(e^{-x}) - \sum_{n=0}^{99}\frac{x^n}{n!}(e^{-x})[/latex]
[latex]f''(x)=-(e^{-x})\frac{x^{98}}{98!}=0[/latex]
Dakle, točka je infleksije 0.
| dalmatinčica (napisa): | http://web.math.pmf.unizg.hr/nastava/analiza/kolokviji/ma2-1011-pop.pdf
kako riješiti 2. zadatak a i b
 |
2. zadatak: a) funkcija je derivabilna samo u 0, a u ostalim nije niti neprekidna.
(Skiciraj si sliku i bit će ti jasno)
Dakle, treba dokazati da postoji [tex]\lim_{x→0}= \frac{f(x)-0}{x-0}[/tex]; sad, mi ne znamo koliko je [tex]f(x)[/tex], jer se k 0 mogu približavati i racionalni i iracionalni (oba su skupa gusta u R); ali kako se i za racionalne i iracionalne, kada x teži u 0, funkcijske vrijednosti približavaju 0 (samo s drugih strana), naslućujemo da je ipak derivabilna. "Uklještimo" izraz s najvećim mogućim slučajem, a to je kad je x iracionalan:
edit:
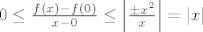
Po teoremu o sendviču, ovaj limes, za x→0, postoji (i jednak je 0).
Kako dokazati da nije derivabilna u svim ostalim točkama? Dovoljno je pokazati da nije neprekidna u tim točkama.
Uzmimo neki niz racionalnih brojeva [tex]a_n \mapsto c [/tex], [tex]c \neq 0[/tex] (to možemo jer je Q gust u R). Slijedi:
[tex]\lim_{n→\infty} f(a_n)=c^2[/tex]
Analogno, uzmemo niz iracionalnih brojeva [tex]b_n \mapsto c [/tex], [tex]c \neq 0[/tex]. Slijedi:
[tex]\lim_{n→\infty} f(b_n)=-c^2[/tex]
[tex]c^2 = - c^2 \Leftrightarrow c=0[/tex]
Kontradikcija.
b) Još bih malo razmislio; ovo za sada znam:
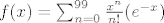
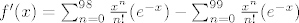
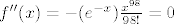
Dakle, točka je infleksije 0.
Zadnja promjena: quark; 12:09 ned, 15. 4. 2012; ukupno mijenjano 3 put/a.
|
|
| [Vrh] |
|
dalmatinčica
Forumaš(ica)


Pridružen/a: 01. 10. 2011. (18:46:54)
Postovi: (AC)16
|
|
| [Vrh] |
|
quark
Forumaš(ica)


Pridružen/a: 22. 10. 2011. (16:47:39)
Postovi: (DA)16
Spol: 
|
|
| [Vrh] |
|
Zenon
Forumaš(ica)


Pridružen/a: 09. 09. 2011. (19:14:43)
Postovi: (2B1)16
Sarma: -
Lokacija: [tex]\pm\infty[/tex]
|
|
| [Vrh] |
|
quark
Forumaš(ica)


Pridružen/a: 22. 10. 2011. (16:47:39)
Postovi: (DA)16
Spol: 
|
 Postano: 15:19 ned, 15. 4. 2012 Naslov: Postano: 15:19 ned, 15. 4. 2012 Naslov: |
    |
|
|
[url=http://web.math.pmf.unizg.hr/nastava/analiza/kol/ma2-0506-kp1.pdf]Treći[/url] odavde:
a) Sinus je neprekidan svugdje, a [tex]\left \lfloor x \right \rfloor[/tex] nije za cijele brojeve; e sad, mi imamo [tex]\left \lfloor x^2 \right \rfloor[/tex], dakle, problematični će biti korijeni prirodnih brojeva.
Formalno se to raspiše gledajući limes slijeva i zdesna za takve brojeve.
Dakle, funkcija je neprekidna u svim točkama osim u (plus/minus) korijenima cijelih brojeva.
b) Sad sama pokušaj ovaj, gledajući koje su najbliže kritične točke oko 1.8 :)
Treći odavde:
a) Sinus je neprekidan svugdje, a [tex]\left \lfloor x \right \rfloor[/tex] nije za cijele brojeve; e sad, mi imamo [tex]\left \lfloor x^2 \right \rfloor[/tex], dakle, problematični će biti korijeni prirodnih brojeva.
Formalno se to raspiše gledajući limes slijeva i zdesna za takve brojeve.
Dakle, funkcija je neprekidna u svim točkama osim u (plus/minus) korijenima cijelih brojeva.
b) Sad sama pokušaj ovaj, gledajući koje su najbliže kritične točke oko 1.8 
Zadnja promjena: quark; 15:20 ned, 15. 4. 2012; ukupno mijenjano 1 put.
|
|
| [Vrh] |
|
jema
Forumaš(ica)

Pridružen/a: 29. 09. 2011. (15:56:35)
Postovi: (52)16
|
|
| [Vrh] |
|
quark
Forumaš(ica)


Pridružen/a: 22. 10. 2011. (16:47:39)
Postovi: (DA)16
Spol: 
|
|
| [Vrh] |
|
Lux86
Forumaš(ica)

Pridružen/a: 11. 09. 2011. (23:38:43)
Postovi: (1D)16
Spol: 
|
|
| [Vrh] |
|
piccola
Forumaš(ica)

Pridružen/a: 30. 11. 2009. (15:39:50)
Postovi: (D7)16
|
|
| [Vrh] |
|
jema
Forumaš(ica)

Pridružen/a: 29. 09. 2011. (15:56:35)
Postovi: (52)16
|
|
| [Vrh] |
|
|












