| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
minnie m.
Forumaš(ica)

Pridružen/a: 06. 10. 2011. (20:34:28)
Postovi: (16)16
|
|
| [Vrh] |
|
ceps
Forumaš(ica)

Pridružen/a: 08. 10. 2010. (13:03:07)
Postovi: (13A)16
|
 Postano: 9:41 pon, 16. 4. 2012 Naslov: Postano: 9:41 pon, 16. 4. 2012 Naslov: |
    |
|
|
1. zadatak, 2. grupa:
Pa samo se zapitaj kako [latex]f_{i, 0}[/latex] djeluje na neki proizvoljan [latex]z \in \mathbb{C}[/latex]:
[latex]f_{i, 0}(z) = iz[/latex]
[latex]f_{i, 0}^2(z) = i^2z[/latex]
[latex]f_{i, 0}^3(z) = i^3z[/latex]
[latex]f_{i, 0}^4(z) = i^4z[/latex]
itd. itd.
([latex]f_{i, 0}^2(z)[/latex] je oznaka za [latex]f_{i, 0}(f_{i, 0}(z))[/latex])
Sada ostaje samo odgovoriti na pitanje što su to [latex]i^2, i^3, i^4 ...[/latex], a vjerujem da se toga sjećaš iz srednje škole.
Ovaj drugi zadatak je malo teži, ali probat ću, pa se javim ovdje ako ga riješim. :D
5. zadatak, 1. grupa:
Iskreno, zbunjuje me njihova uputa i još uvijek ne kužim što su htjeli reći s njom.
Pošto je [latex]G:H = 2[/latex], znamo da je [latex]H \unlhd G[/latex], to se radilo na vježbama pa neću previše objašnjavati.
Onda znamo da možemo stvoriti kvocijentnu grupu [latex]G/H[/latex].
Probaj si nacrtati/zamisliti kako bi to izgledalo - imamo dvije klase, jedna je naravno [latex]H[/latex] a drugu čine svi elementi koji nisu u H.
Sad kad smo obavili pripremu pogledajmo što točno trebamo dokazati: [latex]\forall x \in G, \hspace{2mm} x^2 \in H[/latex].
Očito je da ako je [latex]x \in H[/latex] da je [latex] x^2 \in H[/latex], pošto je H grupa.
Znači, pravi posao treba obaviti dokazivanjem [latex]\forall x \notin H \hspace{2mm}, x^2 \in H[/latex].
U ''pripremi'' smo stvorili kvocijentnu grupu koja dijeli G na dvije klase: H i sve elemente iz G koji nisu iz H, pa ajmo se malo pozabaviti time.
Primijeti da je G/H dvočlana grupa, a sve su dvočlane grupe iste, do na izomorfizam
(Napomena:
Ako označimo dvočlanu grupu sa [latex]\{e, x\}[/latex] imamo:
[latex]ee = e \\ ex = x \\ xe = x \\ xx = e[/latex]
Ako ti nije jasno zašto to mora biti tako, malo si raspiši i vidjet ćeš. )
Za bilo koji [latex]x \notin H[/latex] možemo G/H zapisati kao: [latex]\{H, xH\}[/latex].
Iz gornje priče o dvočlanim grupama slijedi da je [latex]xxH = xH \cdot xH = H[/latex], a iz toga slijedi da [latex]xx \in H[/latex].
(Ovdje pričam o množenju elemenata iz kvocijentne grupe, tj. o množenju klasa, ako te ovo zbunjuje provjeri si kako je ono definirano)
1. zadatak, 2. grupa:
Pa samo se zapitaj kako 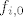 djeluje na neki proizvoljan djeluje na neki proizvoljan 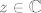 : :
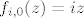
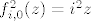
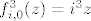
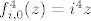
itd. itd.
(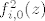 je oznaka za je oznaka za 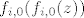 ) )
Sada ostaje samo odgovoriti na pitanje što su to 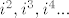 , a vjerujem da se toga sjećaš iz srednje škole. , a vjerujem da se toga sjećaš iz srednje škole.
Ovaj drugi zadatak je malo teži, ali probat ću, pa se javim ovdje ako ga riješim. 
5. zadatak, 1. grupa:
Iskreno, zbunjuje me njihova uputa i još uvijek ne kužim što su htjeli reći s njom.
Pošto je 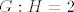 , znamo da je , znamo da je  , to se radilo na vježbama pa neću previše objašnjavati. , to se radilo na vježbama pa neću previše objašnjavati.
Onda znamo da možemo stvoriti kvocijentnu grupu 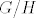 . .
Probaj si nacrtati/zamisliti kako bi to izgledalo - imamo dvije klase, jedna je naravno 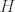 a drugu čine svi elementi koji nisu u H. a drugu čine svi elementi koji nisu u H.
Sad kad smo obavili pripremu pogledajmo što točno trebamo dokazati: 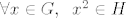 . .
Očito je da ako je 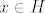 da je da je 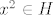 , pošto je H grupa. , pošto je H grupa.
Znači, pravi posao treba obaviti dokazivanjem 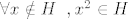 . .
U ''pripremi'' smo stvorili kvocijentnu grupu koja dijeli G na dvije klase: H i sve elemente iz G koji nisu iz H, pa ajmo se malo pozabaviti time.
Primijeti da je G/H dvočlana grupa, a sve su dvočlane grupe iste, do na izomorfizam
(Napomena:
Ako označimo dvočlanu grupu sa 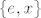 imamo: imamo:
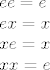
Ako ti nije jasno zašto to mora biti tako, malo si raspiši i vidjet ćeš. )
Za bilo koji 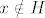 možemo G/H zapisati kao: možemo G/H zapisati kao: 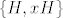 . .
Iz gornje priče o dvočlanim grupama slijedi da je 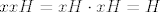 , a iz toga slijedi da , a iz toga slijedi da 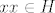 . .
(Ovdje pričam o množenju elemenata iz kvocijentne grupe, tj. o množenju klasa, ako te ovo zbunjuje provjeri si kako je ono definirano)
|
|
| [Vrh] |
|
minnie m.
Forumaš(ica)

Pridružen/a: 06. 10. 2011. (20:34:28)
Postovi: (16)16
|
|
| [Vrh] |
|
Tomy007
Forumaš(ica)

Pridružen/a: 08. 11. 2009. (19:45:28)
Postovi: (94)16
|
|
| [Vrh] |
|
ceps
Forumaš(ica)

Pridružen/a: 08. 10. 2010. (13:03:07)
Postovi: (13A)16
|
|
| [Vrh] |
|
pupi
Forumaš(ica)

Pridružen/a: 20. 12. 2009. (11:03:15)
Postovi: (92)16
Spol: 
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
Lepi91
Forumaš(ica)


Pridružen/a: 15. 09. 2010. (15:22:23)
Postovi: (C8)16
Spol: 
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
pupi
Forumaš(ica)

Pridružen/a: 20. 12. 2009. (11:03:15)
Postovi: (92)16
Spol: 
|
|
| [Vrh] |
|
Lepi91
Forumaš(ica)


Pridružen/a: 15. 09. 2010. (15:22:23)
Postovi: (C8)16
Spol: 
|
|
| [Vrh] |
|
kosani
Forumaš(ica)
Pridružen/a: 14. 11. 2010. (21:22:58)
Postovi: (26)16
|
|
| [Vrh] |
|
ceps
Forumaš(ica)

Pridružen/a: 08. 10. 2010. (13:03:07)
Postovi: (13A)16
|
|
| [Vrh] |
|
kikzmyster
Forumaš(ica)

Pridružen/a: 14. 10. 2010. (13:35:08)
Postovi: (72)16
Spol: 
|
 Postano: 16:06 sri, 18. 4. 2012 Naslov: Postano: 16:06 sri, 18. 4. 2012 Naslov: |
    |
|
|
Evo 27.
Dokazujemo da [latex]H_1 = G_1 \cap H [/latex] zadovoljava one uvjete.
Prvo, neka su [latex] x \in H_1 [/latex] i [latex]h \in H [/latex] proizvoljni. Sad, vrijedi [latex] hxh^{-1} \in G_1 [/latex], jer je [latex]G_1 \unlhd G [/latex] i [latex] x \in G [/latex], a vrijedi i [latex]hxh^{-1} \in H [/latex], jer je [latex] x \in H [/latex] a [latex]H[/latex] je grupa. Dakle, [latex] hxh^{-1} \in G_1 \cap H = H_1[/latex] pa vrijedi [latex]hH_1h^{-1} \subseteq H_1 , \ \forall h \in H[/latex] i to je dovoljno da zakljucimo [latex] H_1 \unlhd H [/latex]. Dalje, [latex]H_1[/latex] je Abelova kao podgrupa (presjek grupa je grupa) Abelove grupe [latex] G_1 [/latex]. I konacno, [latex]H/H_1[/latex] je Abelova jer je [latex]H[/latex] Abelova- [latex]xH_1yH_1 = xyH_1 = yxH_1 = yH_1xH_1 [/latex].
I zna li itko kako se dobije znak za normalnu podgrupu u tex-u?
Evo 27.
Dokazujemo da 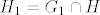 zadovoljava one uvjete. zadovoljava one uvjete.
Prvo, neka su 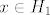 i i 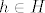 proizvoljni. Sad, vrijedi proizvoljni. Sad, vrijedi 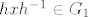 , jer je , jer je  i i 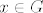 , a vrijedi i , a vrijedi i 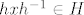 , jer je , jer je 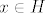 a a 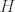 je grupa. Dakle, je grupa. Dakle, 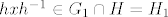 pa vrijedi pa vrijedi 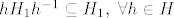 i to je dovoljno da zakljucimo i to je dovoljno da zakljucimo  . Dalje, . Dalje, 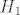 je Abelova kao podgrupa (presjek grupa je grupa) Abelove grupe je Abelova kao podgrupa (presjek grupa je grupa) Abelove grupe 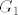 . I konacno, . I konacno, 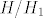 je Abelova jer je je Abelova jer je 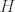 Abelova- Abelova- 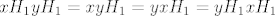 . .
I zna li itko kako se dobije znak za normalnu podgrupu u tex-u?
|
|
| [Vrh] |
|
Tomislav
Forumaš(ica)

Pridružen/a: 04. 10. 2010. (20:18:25)
Postovi: (181)16
Spol: 
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
goranm
Forumaš(ica)


Pridružen/a: 12. 11. 2002. (20:09:12)
Postovi: (906)16
Spol: 
|
 Postano: 16:38 sri, 18. 4. 2012 Naslov: Postano: 16:38 sri, 18. 4. 2012 Naslov: |
    |
|
|
[quote="kosani"]Zadatak 28 mi se čini jednostavnijim (barem ovaj prvi ido)[/quote]
Jer je eH=H, onda jedna lijeva klasa mora biti H. Jer je [G:H]=2 i jer lijeve klase dekomponiraju G, onda preostala klasa mora biti G\H. Na isti način zaključujemo da su H i G\H jedine dvije desne klase. Prema tome, skup lijevih klasa podudara se sa skupom desnih klasa pa je onda H normalna u G. Kako u dokazu nigdje nismo koristili pretpostavku konačnosti grupe G, onda tvrdnja vrijedi i u beskonačnom slučaju.
Što se tiče napomene
[quote]U svezi sa prethodnim zadatkom primjetimo da se rečeni rezultat ne može poopćiti na neki dobar način.[/quote]
nakon zadatka, to baš i nije istina. Zadatak se može poopćiti na sljedeći način:
Neka je G konačna grupa i neka je p najmanji prost broj koji dijeli red od G. Ako je podgrupa H<G td. je [G:H]=p, onda je H normalna u G.
| kosani (napisa): | | Zadatak 28 mi se čini jednostavnijim (barem ovaj prvi ido) |
Jer je eH=H, onda jedna lijeva klasa mora biti H. Jer je [G:H]=2 i jer lijeve klase dekomponiraju G, onda preostala klasa mora biti G\H. Na isti način zaključujemo da su H i G\H jedine dvije desne klase. Prema tome, skup lijevih klasa podudara se sa skupom desnih klasa pa je onda H normalna u G. Kako u dokazu nigdje nismo koristili pretpostavku konačnosti grupe G, onda tvrdnja vrijedi i u beskonačnom slučaju.
Što se tiče napomene
| Citat: | | U svezi sa prethodnim zadatkom primjetimo da se rečeni rezultat ne može poopćiti na neki dobar način. |
nakon zadatka, to baš i nije istina. Zadatak se može poopćiti na sljedeći način:
Neka je G konačna grupa i neka je p najmanji prost broj koji dijeli red od G. Ako je podgrupa H<G td. je [G:H]=p, onda je H normalna u G.
_________________
The Dude Abides
Zadnja promjena: goranm; 16:40 sri, 18. 4. 2012; ukupno mijenjano 1 put.
|
|
| [Vrh] |
|
kosani
Forumaš(ica)
Pridružen/a: 14. 11. 2010. (21:22:58)
Postovi: (26)16
|
|
| [Vrh] |
|
ceps
Forumaš(ica)

Pridružen/a: 08. 10. 2010. (13:03:07)
Postovi: (13A)16
|
|
| [Vrh] |
|
kikzmyster
Forumaš(ica)

Pridružen/a: 14. 10. 2010. (13:35:08)
Postovi: (72)16
Spol: 
|
|
| [Vrh] |
|
|












