| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
penkala
Forumaš(ica)

Pridružen/a: 17. 04. 2012. (14:25:45)
Postovi: (4)16
|
|
| [Vrh] |
|
ceps
Forumaš(ica)

Pridružen/a: 08. 10. 2010. (13:03:07)
Postovi: (13A)16
|
 Postano: 15:24 uto, 17. 4. 2012 Naslov: Postano: 15:24 uto, 17. 4. 2012 Naslov: |
    |
|
|
Oni u tom primjeru gledaju ''položeni sladoled'', kao ovaj tu:
http://www.wolframalpha.com/input/?i=-tan%28pi%2F6%29x%3C+z+%3Ctan%28pi%2F6%29x%2C+x+%3E+0
Potpuno je svejedno gledaju li takav ''sladoled'', ili uspravni sladoled kao ovaj tu:
http://www.wolframalpha.com/input/?i=-tan%28pi%2F6%29z%3C+x+%3Ctan%28pi%2F6%29z%2C+z+%3E+0
(jer obadva sladoleda imaju isti volumen).
No u zadatku o kojem smo ovdje pričali cijelo vrijeme, imamo poprilično jasno rečeno da gledamo uspravni slučaj (spominje se ravnina [latex]z = \sqrt{3}[/latex]).
Plus, imamo i funkciju [tex]\frac{z}{x^2+y^2+z^2}[/tex] koja ne bi bila ista da gledamo taj položeni slučaj, pa ni integral ne bi bio isti.
@satja
[quote="satja"][quote="ceps"]@pupi
Za EDIT1: možemo. To možemo kod svakog tijela kod kojeg dobijemo krugove ako ga ''narežemo na šnitice''.
I da, integral bude
[latex]\displaystyle\int_{\sqrt{3}}^2 \pi(4 - z^2) dz [/latex][/quote]
Ne mozemo. Mi ne trazimo volumen tijela, nego integriramo funkciju [tex]\frac{z}{x^2+y^2+z^2}[/tex].
I zadatak se stvarno moze shvatiti na dva razlicita nacina. Je li D podrucje iznad ravnine a unutar sfere, ili ispod ravnine a unutar sfere?[/quote]
Imaš pravo, i sam sam zaboravio na tu funkciju ovoliko raspravljajući o jednom zadatku. :D
A da, može se shvatiti na dva načina. Meni je nekako logičnije bilo ovako.
Oni u tom primjeru gledaju ''položeni sladoled'', kao ovaj tu:
http://www.wolframalpha.com/input/?i=-tan%28pi%2F6%29x%3C+z+%3Ctan%28pi%2F6%29x%2C+x+%3E+0
Potpuno je svejedno gledaju li takav ''sladoled'', ili uspravni sladoled kao ovaj tu:
http://www.wolframalpha.com/input/?i=-tan%28pi%2F6%29z%3C+x+%3Ctan%28pi%2F6%29z%2C+z+%3E+0
(jer obadva sladoleda imaju isti volumen).
No u zadatku o kojem smo ovdje pričali cijelo vrijeme, imamo poprilično jasno rečeno da gledamo uspravni slučaj (spominje se ravnina 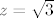 ). ).
Plus, imamo i funkciju [tex]\frac{z}{x^2+y^2+z^2}[/tex] koja ne bi bila ista da gledamo taj položeni slučaj, pa ni integral ne bi bio isti.
@satja
| satja (napisa): | | ceps (napisa): | @pupi
Za EDIT1: možemo. To možemo kod svakog tijela kod kojeg dobijemo krugove ako ga ''narežemo na šnitice''.
I da, integral bude
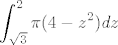 |
Ne mozemo. Mi ne trazimo volumen tijela, nego integriramo funkciju [tex]\frac{z}{x^2+y^2+z^2}[/tex].
I zadatak se stvarno moze shvatiti na dva razlicita nacina. Je li D podrucje iznad ravnine a unutar sfere, ili ispod ravnine a unutar sfere? |
Imaš pravo, i sam sam zaboravio na tu funkciju ovoliko raspravljajući o jednom zadatku. 
A da, može se shvatiti na dva načina. Meni je nekako logičnije bilo ovako.
|
|
| [Vrh] |
|
satja
Forumaš(ica)

Pridružen/a: 16. 05. 2010. (10:44:17)
Postovi: (F1)16
|
|
| [Vrh] |
|
ceps
Forumaš(ica)

Pridružen/a: 08. 10. 2010. (13:03:07)
Postovi: (13A)16
|
|
| [Vrh] |
|
A_je_to
Forumaš(ica)

Pridružen/a: 19. 02. 2009. (16:51:22)
Postovi: (6D)16
Spol: 
|
|
| [Vrh] |
|
marty
Forumaš(ica)
Pridružen/a: 26. 10. 2009. (17:40:41)
Postovi: (3D)16
Spol: 
|
|
| [Vrh] |
|
minora665
Forumaš(ica)

Pridružen/a: 10. 02. 2010. (22:52:01)
Postovi: (1F)16
|
|
| [Vrh] |
|
mapat
Forumaš(ica)
Pridružen/a: 01. 11. 2010. (15:31:40)
Postovi: (10)16
Spol: 
|
|
| [Vrh] |
|
pupi
Forumaš(ica)

Pridružen/a: 20. 12. 2009. (11:03:15)
Postovi: (92)16
Spol: 
|
|
| [Vrh] |
|
mapat
Forumaš(ica)
Pridružen/a: 01. 11. 2010. (15:31:40)
Postovi: (10)16
Spol: 
|
|
| [Vrh] |
|
Tomob
Forumaš(ica)

Pridružen/a: 04. 03. 2012. (09:15:50)
Postovi: (A)16
|
 Postano: 13:28 sri, 18. 4. 2012 Naslov: Postano: 13:28 sri, 18. 4. 2012 Naslov: |
    |
|
|
Pozdrav,
može li mi netko pomoći s 1.a zadatkom i 2010/2011. Kako trebamo izracunati površinu izvan kružnice, a unutar kardioide, moja je ideja buila ta da odredima za koje sve kuteve φ naša kružnica i kardioida imaju jednake r-ove.
Za kružnicu: r=2acos(φ)
Za kardioidu: r=a(1+cos(φ))
4 su moguća kuta: 0, π i još neka dva koja mene zanimaju. Mislio sam računati integral u granicama r element od a(radijus krušnice) do a(1+cos(φ)), a kut φ bi mi bio u granicama od ona preostala dva kuta za koje kardioida i kružnica imaju isti r. Te kuteve sam planirao izračinat tako da izjednačim r-ove, ali mi ona ispadne samo jedan φ=0.
Moja pitanja su: Može li se to riješiti na način na koji sam si zamislio i ako može, kako dobiti ta φ koji mi treba?
Pozdrav,
može li mi netko pomoći s 1.a zadatkom i 2010/2011. Kako trebamo izracunati površinu izvan kružnice, a unutar kardioide, moja je ideja buila ta da odredima za koje sve kuteve φ naša kružnica i kardioida imaju jednake r-ove.
Za kružnicu: r=2acos(φ)
Za kardioidu: r=a(1+cos(φ))
4 su moguća kuta: 0, π i još neka dva koja mene zanimaju. Mislio sam računati integral u granicama r element od a(radijus krušnice) do a(1+cos(φ)), a kut φ bi mi bio u granicama od ona preostala dva kuta za koje kardioida i kružnica imaju isti r. Te kuteve sam planirao izračinat tako da izjednačim r-ove, ali mi ona ispadne samo jedan φ=0.
Moja pitanja su: Može li se to riješiti na način na koji sam si zamislio i ako može, kako dobiti ta φ koji mi treba?
|
|
| [Vrh] |
|
Jess
Forumaš(ica)

Pridružen/a: 07. 09. 2011. (14:34:48)
Postovi: (2)16
Spol: 
|
|
| [Vrh] |
|
pupi
Forumaš(ica)

Pridružen/a: 20. 12. 2009. (11:03:15)
Postovi: (92)16
Spol: 
|
|
| [Vrh] |
|
Tomob
Forumaš(ica)

Pridružen/a: 04. 03. 2012. (09:15:50)
Postovi: (A)16
|
|
| [Vrh] |
|
jabuka
Forumaš(ica)
Pridružen/a: 21. 11. 2009. (15:53:14)
Postovi: (7C)16
|
|
| [Vrh] |
|
meda
Forumaš(ica)

Pridružen/a: 09. 01. 2010. (09:29:23)
Postovi: (A0)16
|
|
| [Vrh] |
|
ceps
Forumaš(ica)

Pridružen/a: 08. 10. 2010. (13:03:07)
Postovi: (13A)16
|
|
| [Vrh] |
|
Joker
Forumaš(ica)

Pridružen/a: 19. 09. 2010. (10:19:16)
Postovi: (8C)16
Spol: 
|
|
| [Vrh] |
|
kosani
Forumaš(ica)
Pridružen/a: 14. 11. 2010. (21:22:58)
Postovi: (26)16
|
|
| [Vrh] |
|
888
Forumaš(ica)

Pridružen/a: 09. 10. 2010. (18:26:14)
Postovi: (29)16
|
 Postano: 17:52 sri, 18. 4. 2012 Naslov: Postano: 17:52 sri, 18. 4. 2012 Naslov: |
    |
|
|
Pa šta nije pod c) da postoji? Recimo Q2 presjek [0,1]x[0,1] nema površinu, zatvarač je R2 presjek [0,1]x[0,1] i on ima površinu
Pa šta nije pod c) da postoji? Recimo Q2 presjek [0,1]x[0,1] nema površinu, zatvarač je R2 presjek [0,1]x[0,1] i on ima površinu
|
|
| [Vrh] |
|
|












