| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
Bug
Forumaš(ica)


Pridružen/a: 06. 04. 2003. (17:31:11)
Postovi: (1A9)16
Spol: 
Lokacija: Kako kad!!
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
Tomislav
Forumaš(ica)

Pridružen/a: 04. 10. 2010. (20:18:25)
Postovi: (181)16
Spol: 
|
|
| [Vrh] |
|
kslaven
Forumaš(ica)

Pridružen/a: 17. 10. 2010. (18:07:06)
Postovi: (52)16
Spol: 
|
|
| [Vrh] |
|
ludamath
Forumaš(ica)


Pridružen/a: 06. 02. 2008. (16:00:14)
Postovi: (3E)16
Spol: 
|
|
| [Vrh] |
|
kslaven
Forumaš(ica)

Pridružen/a: 17. 10. 2010. (18:07:06)
Postovi: (52)16
Spol: 
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
kslaven
Forumaš(ica)

Pridružen/a: 17. 10. 2010. (18:07:06)
Postovi: (52)16
Spol: 
|
|
| [Vrh] |
|
kkarlo
Forumaš(ica)

Pridružen/a: 19. 05. 2010. (08:43:59)
Postovi: (1B2)16
Spol: 
|
|
| [Vrh] |
|
kkarlo
Forumaš(ica)

Pridružen/a: 19. 05. 2010. (08:43:59)
Postovi: (1B2)16
Spol: 
|
|
| [Vrh] |
|
kslaven
Forumaš(ica)

Pridružen/a: 17. 10. 2010. (18:07:06)
Postovi: (52)16
Spol: 
|
|
| [Vrh] |
|
pravipurger
Forumaš(ica)


Pridružen/a: 11. 07. 2009. (10:29:44)
Postovi: (128)16
Spol: 
|
|
| [Vrh] |
|
GODIMENTI
Forumaš(ica)
Pridružen/a: 15. 02. 2011. (13:15:40)
Postovi: (9)16
|
|
| [Vrh] |
|
jackass9
Forumaš(ica)

Pridružen/a: 19. 09. 2009. (10:23:58)
Postovi: (15D)16
Spol: 
Lokacija: pod stolom
|
 Postano: 21:58 čet, 24. 5. 2012 Naslov: Postano: 21:58 čet, 24. 5. 2012 Naslov: |
    |
|
|
[quote="GODIMENTI"]Može li asistent dati rješenja i postupak 2.blica za nastavnički smjer?
Ja sam se ubio u dokazivanju prstena, i za sve to nula bodova?
Onda sam stvarno idiot![/quote]
pa morao si samo provjerit A-B i A*B, za neke A i B iz onog kaj ti je bilo zadano...naravno, uz to ide i popratni tekst, ali poanta je da provjeriš to dvoje, a to ti dva reda
| GODIMENTI (napisa): | Može li asistent dati rješenja i postupak 2.blica za nastavnički smjer?
Ja sam se ubio u dokazivanju prstena, i za sve to nula bodova?
Onda sam stvarno idiot! |
pa morao si samo provjerit A-B i A*B, za neke A i B iz onog kaj ti je bilo zadano...naravno, uz to ide i popratni tekst, ali poanta je da provjeriš to dvoje, a to ti dva reda
_________________
Nema mozga do malog mozga
|
|
| [Vrh] |
|
di_
Gost
|
|
| [Vrh] |
|
di_
Gost
|
|
| [Vrh] |
|
goranm
Forumaš(ica)


Pridružen/a: 12. 11. 2002. (20:09:12)
Postovi: (906)16
Spol: 
|
 Postano: 3:27 sub, 26. 5. 2012 Naslov: Postano: 3:27 sub, 26. 5. 2012 Naslov: |
    |
|
|
[quote="di_"]a zasto neki puta kada provjeravamo da li je nesto prsten provjeravamo je li operacija zatvorena na a-b i a+b a neki puta a-b i a*b?
* Tj. nekad a-b nekad a+b
[/quote]
Mala primjedba: za provjeriti da je nešto [b]prsten[/b], bez referiranja na neki nadprsten (tj. nadskup koji je prsten) moraju se ispitati sva svojstva iz definicije, tj. asocijativnost zbrajanja i množenja, postojanje inverznog elementa s obzorim na zbrajanje, postojanje nule, komutativnost zbrajanja i da vrijede zakoni distribucije množenja nad zbrajanjem.
Za provjeriti da je neki skup X [b]pot[/b]prsten nekog otprije poznatog prstena [latex]A\supseteq X[/latex] dovoljno je provjeriti da je zadovoljeno [latex]a-b, a\cdot b \in X[/latex], za svaka dva [latex]a,b\in X[/latex].
Zašto se neki put provjerava a-b, a neki put a+b, pretpostavljam da se radi o ova dva slučaja: ili se radi o grešci pa umjesto a+b treba provjeriti a-b ili je očito da je za svaki a iz X ujedno i -a u X pa ostaje provjeriti da je još a+b u X (ekvivalentno je provjeriti da je ili samo a-b u X, za svaka dva a,b u X ili da je -a te a+b u X, za svaka dva a,b iz X).
| di_ (napisa): | a zasto neki puta kada provjeravamo da li je nesto prsten provjeravamo je li operacija zatvorena na a-b i a+b a neki puta a-b i a*b?
* Tj. nekad a-b nekad a+b
|
Mala primjedba: za provjeriti da je nešto prsten, bez referiranja na neki nadprsten (tj. nadskup koji je prsten) moraju se ispitati sva svojstva iz definicije, tj. asocijativnost zbrajanja i množenja, postojanje inverznog elementa s obzorim na zbrajanje, postojanje nule, komutativnost zbrajanja i da vrijede zakoni distribucije množenja nad zbrajanjem.
Za provjeriti da je neki skup X potprsten nekog otprije poznatog prstena 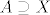 dovoljno je provjeriti da je zadovoljeno dovoljno je provjeriti da je zadovoljeno 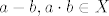 , za svaka dva , za svaka dva 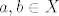 . .
Zašto se neki put provjerava a-b, a neki put a+b, pretpostavljam da se radi o ova dva slučaja: ili se radi o grešci pa umjesto a+b treba provjeriti a-b ili je očito da je za svaki a iz X ujedno i -a u X pa ostaje provjeriti da je još a+b u X (ekvivalentno je provjeriti da je ili samo a-b u X, za svaka dva a,b u X ili da je -a te a+b u X, za svaka dva a,b iz X).
_________________
The Dude Abides
|
|
| [Vrh] |
|
|
















