| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
sys_
Forumaš(ica)
Pridružen/a: 01. 11. 2011. (11:19:00)
Postovi: (20)16
|
|
| [Vrh] |
|
quark
Forumaš(ica)
Pridružen/a: 22. 10. 2011. (16:47:39)
Postovi: (DA)16
Spol: 
|
 Postano: 23:12 sub, 2. 6. 2012 Naslov: Re: kvadratna matrica i determinanta |
    |
|
|
[quote="sys_"]Za kvadratnu maticu A e Mn(F) vrijedi da je r(A) =n akko determinanta A različita od 0 ( r(A)<n akko det A =0). Kako pokazati obrnuti smjer ? Hvala :)[/quote]
Koji ti smjer nije jasan? Akko označuje ekvivalenciju pa ne možemo znati koja ti implikacija nije jasna. Ali eto, evo obje:
1.[tex]r(a)=n \Rightarrow det(A)\neq 0[/tex]
Ako je r(A)= n, onda je matrica ekvivalentna jediničnoj matrici, tj. A se može u konačno mnogo koraka pretvoriti u I; sve te matrice kojima izvodimo te korake regularne su pa zbog Binet - Cauchyjeva teorema, pa je i A regularna.
2.[tex]r(a)=n \Leftarrow det(A)\neq 0[/tex]
Pretpostavimo suprotno; po definiciji, to znači da su matrici stupci/retci linearno zavisni. Uzmimo na primjer jedan linearno zavisan netrivijalan redak (ako je trivijalan, gotovi smo); to znači da se on može prikazati kao netrivijalna linearna kombinacija ostalih vektora - dakle, možemo svesti taj redak na nulredak bez da množimo nul-skalarom (probaj sam/a zaključiti kakvim skalarom treba množiti koji redak), tj. el. transformacijama. Takvoj je matrici determinanta 0. A kako smo koristili samo el. transformacije, slijedi da je i determinanta početne matrice također 0. Kontradikcija.
| sys_ (napisa): | Za kvadratnu maticu A e Mn(F) vrijedi da je r(A) =n akko determinanta A različita od 0 ( r(A)<n akko det A =0). Kako pokazati obrnuti smjer ? Hvala  |
Koji ti smjer nije jasan? Akko označuje ekvivalenciju pa ne možemo znati koja ti implikacija nije jasna. Ali eto, evo obje:
1.[tex]r(a)=n \Rightarrow det(A)\neq 0[/tex]
Ako je r(A)= n, onda je matrica ekvivalentna jediničnoj matrici, tj. A se može u konačno mnogo koraka pretvoriti u I; sve te matrice kojima izvodimo te korake regularne su pa zbog Binet - Cauchyjeva teorema, pa je i A regularna.
2.[tex]r(a)=n \Leftarrow det(A)\neq 0[/tex]
Pretpostavimo suprotno; po definiciji, to znači da su matrici stupci/retci linearno zavisni. Uzmimo na primjer jedan linearno zavisan netrivijalan redak (ako je trivijalan, gotovi smo); to znači da se on može prikazati kao netrivijalna linearna kombinacija ostalih vektora - dakle, možemo svesti taj redak na nulredak bez da množimo nul-skalarom (probaj sam/a zaključiti kakvim skalarom treba množiti koji redak), tj. el. transformacijama. Takvoj je matrici determinanta 0. A kako smo koristili samo el. transformacije, slijedi da je i determinanta početne matrice također 0. Kontradikcija.
Zadnja promjena: quark; 1:28 ned, 3. 6. 2012; ukupno mijenjano 2 put/a.
|
|
| [Vrh] |
|
sys_
Forumaš(ica)
Pridružen/a: 01. 11. 2011. (11:19:00)
Postovi: (20)16
|
|
| [Vrh] |
|
quark
Forumaš(ica)
Pridružen/a: 22. 10. 2011. (16:47:39)
Postovi: (DA)16
Spol:
|
| Postano: 1:10 ned, 3. 6. 2012 Naslov: |
|
|
|
Ne razumjesmo se :)
Ako pretpostaviš da je rang matrice manji od n, onda su joj linearno zavisni i retci i stupci. Ja sam rekao "na primjer", a trebao sam" bez smanjena općenitosti uzmimo redak, a ne stupac."
Dakle, sad ćeš vidjeti da nul-redak/stupac nije izdvojen slučaj, nego da ćemo [b]svaki[/b] zavisni redak/stupac pomoću el. transformacija svesti na nul-redak/stupac.
Da ne kompliciram, uzmimo sve retke [tex]\{R_1,..., R_n\}[/tex], pronađemo taj zavisni, recimo [tex]R_k[/tex] i napišemo ga pomoću ostalih:
[tex]R_k = \sum_{i=1,i\neq k}^{n}\alpha_iR_i[/tex]
I što sada radimo da taj zavisni svedemo na nul-redak? Moramo svaki redak [tex]R_i[/tex] pomnožiti s [tex]-\alpha_i[/tex], [tex]\forall i \neq k[/tex], i dodati ga tom k-tom retku.
Na primjer, imaš matricu:
[latex]\left( \begin{array}{ccc}
1 & 0 & 0 \\
0 & 1 & 0 \\
2 & -3 & 0 \end{array} \right)[/latex]
Treći je redak očigledno zavisan i zapišemo ga [tex]R_3 = 2\cdot R_1 + (-3)\cdot R_2[/tex]; onda prvi redak moramo pomnožiti s [tex]-2[/tex] i drugi s [tex]3[/tex] te ih dodati trećem:
[latex]\left( \begin{array}{ccc}
1 & 0 & 0 \\
0 & 1 & 0 \\
0 & 0 & 0 \end{array} \right)[/latex]
Eto. :wink:
Ne razumjesmo se
Ako pretpostaviš da je rang matrice manji od n, onda su joj linearno zavisni i retci i stupci. Ja sam rekao "na primjer", a trebao sam" bez smanjena općenitosti uzmimo redak, a ne stupac."
Dakle, sad ćeš vidjeti da nul-redak/stupac nije izdvojen slučaj, nego da ćemo svaki zavisni redak/stupac pomoću el. transformacija svesti na nul-redak/stupac.
Da ne kompliciram, uzmimo sve retke [tex]\{R_1,..., R_n\}[/tex], pronađemo taj zavisni, recimo [tex]R_k[/tex] i napišemo ga pomoću ostalih:
[tex]R_k = \sum_{i=1,i\neq k}^{n}\alpha_iR_i[/tex]
I što sada radimo da taj zavisni svedemo na nul-redak? Moramo svaki redak [tex]R_i[/tex] pomnožiti s [tex]-\alpha_i[/tex], [tex]\forall i \neq k[/tex], i dodati ga tom k-tom retku.
Na primjer, imaš matricu:
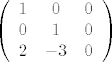
Treći je redak očigledno zavisan i zapišemo ga [tex]R_3 = 2\cdot R_1 + (-3)\cdot R_2[/tex]; onda prvi redak moramo pomnožiti s [tex]-2[/tex] i drugi s [tex]3[/tex] te ih dodati trećem:
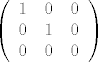
Eto. 
|
|
| [Vrh] |
|
sys_
Forumaš(ica)
Pridružen/a: 01. 11. 2011. (11:19:00)
Postovi: (20)16
|
|
| [Vrh] |
|
quark
Forumaš(ica)
Pridružen/a: 22. 10. 2011. (16:47:39)
Postovi: (DA)16
Spol:
|
|
| [Vrh] |
|
|
