| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
ceps
Forumaš(ica)

Pridružen/a: 08. 10. 2010. (13:03:07)
Postovi: (13A)16
|
|
| [Vrh] |
|
kikzmyster
Forumaš(ica)

Pridružen/a: 14. 10. 2010. (13:35:08)
Postovi: (72)16
Spol: 
|
 Postano: 11:06 pon, 4. 6. 2012 Naslov: Postano: 11:06 pon, 4. 6. 2012 Naslov: |
    |
|
|
to sam se isto pitao, sto je rub ovih "zatvorenih" ploha (kao, sta je rub sfere?), i jedino sto mi se cini da moze bit je slika ruba od skupa Q nad kojim djeluje parametrizacija. Npr, ako parametriziramo sferu, onda gledamo [tex]\varphi \colon Q=[0,\pi]\times[0,2\pi] \rightarrow \mathbb(R)^3[/tex], pa je onda rub sfere slika od [tex]\partial Q[/tex] (dobije se desna polovica kruznice uz z-os).
Mislim, meni je i dalje logicnije da je rub sfere ta cijela sfera, ali bi onda svaka ploha u R^3 bila sama svoj rub
EDIT: ili sfera jednostavno nema rub (pogledaj http://www.physicsforums.com/archive/index.php/t-74187.html), pa bi onda po ovome rub stosca valjda bila ona kruznica baze i tocka na vrhu
@A_je_to - dakle kao sto si rekao, imamo parametrizacije za ove dvije kruznice [tex]\gamma_1(t) = (\cos t + 1, \sin t) \, , \, \gamma_2(t) = (\cos t, \sin t + 1) [/tex], ali sad, kako gledamo samo ovaj vanjski rub njihove unije, za [tex]\gamma_1[/tex] ce bit [tex]t \in [- \pi, \pi/2][/tex], a za [tex]\gamma_2[/tex] ce bit [tex]t \in [0,3\pi /2] [/tex]. Znaci racunamo [tex]\displaystyle \int_{\gamma_1} \omega + \int_{\gamma_2} \omega = \int_{-\pi}^{\pi /2}\omega(\gamma_1(t))\cdot \gamma_1
'(t)\, dt + \int_{0}^{3\pi /2}\omega(\gamma_2(t))\cdot \gamma_2
'(t)\, dt [/tex].
to sam se isto pitao, sto je rub ovih "zatvorenih" ploha (kao, sta je rub sfere?), i jedino sto mi se cini da moze bit je slika ruba od skupa Q nad kojim djeluje parametrizacija. Npr, ako parametriziramo sferu, onda gledamo [tex]\varphi \colon Q=[0,\pi]\times[0,2\pi] \rightarrow \mathbb(R)^3[/tex], pa je onda rub sfere slika od [tex]\partial Q[/tex] (dobije se desna polovica kruznice uz z-os).
Mislim, meni je i dalje logicnije da je rub sfere ta cijela sfera, ali bi onda svaka ploha u R^3 bila sama svoj rub
EDIT: ili sfera jednostavno nema rub (pogledaj http://www.physicsforums.com/archive/index.php/t-74187.html), pa bi onda po ovome rub stosca valjda bila ona kruznica baze i tocka na vrhu
@A_je_to - dakle kao sto si rekao, imamo parametrizacije za ove dvije kruznice [tex]\gamma_1(t) = (\cos t + 1, \sin t) \, , \, \gamma_2(t) = (\cos t, \sin t + 1) [/tex], ali sad, kako gledamo samo ovaj vanjski rub njihove unije, za [tex]\gamma_1[/tex] ce bit [tex]t \in [- \pi, \pi/2][/tex], a za [tex]\gamma_2[/tex] ce bit [tex]t \in [0,3\pi /2] [/tex]. Znaci racunamo [tex]\displaystyle \int_{\gamma_1} \omega + \int_{\gamma_2} \omega = \int_{-\pi}^{\pi /2}\omega(\gamma_1(t))\cdot \gamma_1
'(t)\, dt + \int_{0}^{3\pi /2}\omega(\gamma_2(t))\cdot \gamma_2
'(t)\, dt [/tex].
|
|
| [Vrh] |
|
ceps
Forumaš(ica)

Pridružen/a: 08. 10. 2010. (13:03:07)
Postovi: (13A)16
|
|
| [Vrh] |
|
Joker
Forumaš(ica)

Pridružen/a: 19. 09. 2010. (10:19:16)
Postovi: (8C)16
Spol: 
|
|
| [Vrh] |
|
ceps
Forumaš(ica)

Pridružen/a: 08. 10. 2010. (13:03:07)
Postovi: (13A)16
|
 Postano: 13:09 pon, 4. 6. 2012 Naslov: Postano: 13:09 pon, 4. 6. 2012 Naslov: |
    |
|
|
http://web.math.pmf.unizg.hr/nastava/difraf/int/pred/p_o21.pdf
Na vrhu zadnje stranice ti piše kako se definira jedinična normala. Tebi u ovom zadatku normala ne treba biti jedinična (kažu da mora biti oblika [latex]c(1,1,1)[/latex] ), pa možeš zanemariti ovo dijeljenje normom.
Ti trebaš ''namjestiti'' parametrizaciju tako da bude pravilno orijentirana. Napiši si na početku parametrizaciju kakvu god hoćeš, dobit ćeš normalu oblika [latex]c(1,1,1)[/latex] ili [latex]-c(1,1,1)[/latex].
Ako je ovaj prvi oblik, super. Ako dobiješ ovaj drugi, trebaš samo ''promijeniti smjer'' (promijeniti orijentaciju) parametrizacije.
Javi ako zapneš negdje.
http://web.math.pmf.unizg.hr/nastava/difraf/int/pred/p_o21.pdf
Na vrhu zadnje stranice ti piše kako se definira jedinična normala. Tebi u ovom zadatku normala ne treba biti jedinična (kažu da mora biti oblika 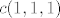 ), pa možeš zanemariti ovo dijeljenje normom. ), pa možeš zanemariti ovo dijeljenje normom.
Ti trebaš ''namjestiti'' parametrizaciju tako da bude pravilno orijentirana. Napiši si na početku parametrizaciju kakvu god hoćeš, dobit ćeš normalu oblika 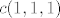 ili ili 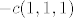 . .
Ako je ovaj prvi oblik, super. Ako dobiješ ovaj drugi, trebaš samo ''promijeniti smjer'' (promijeniti orijentaciju) parametrizacije.
Javi ako zapneš negdje.
|
|
| [Vrh] |
|
pmli
Forumaš(ica)

Pridružen/a: 09. 11. 2009. (12:03:05)
Postovi: (2C8)16
Spol: 
|
 Postano: 16:20 pon, 4. 6. 2012 Naslov: Postano: 16:20 pon, 4. 6. 2012 Naslov: |
    |
|
|
[quote="markos"]jel netko moze rjesiti 1.,4. i 5. zad iz kolokvija2011
http://web.math.pmf.unizg.hr/nastava/difraf/int/2010-11/kolokvij2.pdf
i nije mi bas jasno, kako, ako znamo potencijal podintegralne funkcije, dobiti integral....npr u 2. postu ove teme???[/quote]
Pogledaj Tm 16.10.
[quote="ceps"]http://web.math.pmf.unizg.hr/nastava/difraf/int/2010-11/kolokvij2.pdf
5. zadatak
Ploha s kojom radimo je nekakav plašt stošca. Moje pitanje je: što bi bio rub te plohe?
(Po teoremu o rotaciji trebamo računati , gdje je D ta ploha).[/quote]
Rub je kružnica [latex]x^2 + y^2 = 4[/latex], [latex]z = 0[/latex].
[quote="Joker"]imam pitanje u vezi treceg zadatka ovdje, http://web.math.pmf.unizg.hr/nastava/ma34/ma4/2005-06/rj3.pdf
( ovo su rješenja ali je napisani tekst zadatka prije svakog)
zasto smo kasnije mogli zamijeniti parametrizaciju y(t)=(a/2*cost, 0, a*sint)[/quote]
Rečeno je, [latex]F[/latex] ne ovisi o [latex]y[/latex], pa je sasvim svejedno što se nalazi na 2. komponenti.
[quote="Joker"]sa parametrizacijom y(t)=(cost,0,sint) ?[/quote]
Pogađam da, kako se radi o MA4, što je vjerojatno predavao prof. Ungar, da su oni na raspolaganju imali neke teoreme o homotopnim putevima...
[quote="Joker"]i na kraju,jel rješenje 18pi ako se ovako rjesava a ne 9pi?[/quote]
Da, rješenje je [latex]18\pi[/latex].
[quote="Joker"]takoder, jesmo li mogli napisati samo parametrizaciju od npr -pi do pi i pomnoziti s 9 na kraju?[/quote]
Da, jer se radi o zbrajanju puteva.
[quote="kikzmyster"]to sam se isto pitao, sto je rub ovih "zatvorenih" ploha (kao, sta je rub sfere?), i jedino sto mi se cini da moze bit je slika ruba od skupa Q nad kojim djeluje parametrizacija. Npr, ako parametriziramo sferu, onda gledamo [tex]\varphi \colon Q=[0,\pi]\times[0,2\pi] \rightarrow \mathbb(R)^3[/tex], pa je onda rub sfere slika od [tex]\partial Q[/tex] (dobije se desna polovica kruznice uz z-os).
Mislim, meni je i dalje logicnije da je rub sfere ta cijela sfera, ali bi onda svaka ploha u R^3 bila sama svoj rub[/quote]
[quote="ceps"]@kikzmyster
Da, čini mi se da si u pravu jer taj teorem u skripti kaže nekako ''Neka je D orijentirana kompaktna 2-ploha s rubom'', što implicira da nemaju baš sve plohe rub.
A rub 2-plohe bi trebala biti neka krivulja (1D objekt), tako da mi nije baš logično da je neka ploha ''sama sebi rub''.[/quote]
Po ovome zaključujem, kao ni prošle godine, na predavanju nisu objašnjeni rubovi, pa vam ne mogu dati točan odgovor. Da, prirodno je uzeti da je rub plohe slika ruba domene neke parametrizacije. Problem nam se onda javlja kod sfere jer za nju postoji više parametrizacija, što bi povlačilo da rub ovisi o parametrizaciji, a to nije dobro. Htjeli bi, naravno, da rub ovisi samo o plohi. Ono što mi je čudno što se definira da karta za domenu mora imati zatvoreni kvadar. Mislim da kad bi se dopuštali samo otvoreni skupovi za domene (kao što se radi na MMF-u), onda bi imali neku vrstu jedinstvenosti (možda se grdno varam). Tada sfera ne bi bila ni 2-čelija.
Moj vam je savjet da se držite intuicije. :) Znači, rub je ono gdje se možete porezati. :D
Pogledaj Tm 16.10.
| ceps (napisa): | http://web.math.pmf.unizg.hr/nastava/difraf/int/2010-11/kolokvij2.pdf
5. zadatak
Ploha s kojom radimo je nekakav plašt stošca. Moje pitanje je: što bi bio rub te plohe?
(Po teoremu o rotaciji trebamo računati , gdje je D ta ploha). |
Rub je kružnica 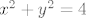 , , 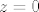 . .
Rečeno je, 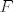 ne ovisi o ne ovisi o  , pa je sasvim svejedno što se nalazi na 2. komponenti. , pa je sasvim svejedno što se nalazi na 2. komponenti.
| Joker (napisa): | | sa parametrizacijom y(t)=(cost,0,sint) ? |
Pogađam da, kako se radi o MA4, što je vjerojatno predavao prof. Ungar, da su oni na raspolaganju imali neke teoreme o homotopnim putevima...
| Joker (napisa): | | i na kraju,jel rješenje 18pi ako se ovako rjesava a ne 9pi? |
Da, rješenje je 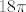 . .
| Joker (napisa): | | takoder, jesmo li mogli napisati samo parametrizaciju od npr -pi do pi i pomnoziti s 9 na kraju? |
Da, jer se radi o zbrajanju puteva.
| kikzmyster (napisa): | to sam se isto pitao, sto je rub ovih "zatvorenih" ploha (kao, sta je rub sfere?), i jedino sto mi se cini da moze bit je slika ruba od skupa Q nad kojim djeluje parametrizacija. Npr, ako parametriziramo sferu, onda gledamo [tex]\varphi \colon Q=[0,\pi]\times[0,2\pi] \rightarrow \mathbb(R)^3[/tex], pa je onda rub sfere slika od [tex]\partial Q[/tex] (dobije se desna polovica kruznice uz z-os).
Mislim, meni je i dalje logicnije da je rub sfere ta cijela sfera, ali bi onda svaka ploha u R^3 bila sama svoj rub |
| ceps (napisa): | @kikzmyster
Da, čini mi se da si u pravu jer taj teorem u skripti kaže nekako ''Neka je D orijentirana kompaktna 2-ploha s rubom'', što implicira da nemaju baš sve plohe rub.
A rub 2-plohe bi trebala biti neka krivulja (1D objekt), tako da mi nije baš logično da je neka ploha ''sama sebi rub''. |
Po ovome zaključujem, kao ni prošle godine, na predavanju nisu objašnjeni rubovi, pa vam ne mogu dati točan odgovor. Da, prirodno je uzeti da je rub plohe slika ruba domene neke parametrizacije. Problem nam se onda javlja kod sfere jer za nju postoji više parametrizacija, što bi povlačilo da rub ovisi o parametrizaciji, a to nije dobro. Htjeli bi, naravno, da rub ovisi samo o plohi. Ono što mi je čudno što se definira da karta za domenu mora imati zatvoreni kvadar. Mislim da kad bi se dopuštali samo otvoreni skupovi za domene (kao što se radi na MMF-u), onda bi imali neku vrstu jedinstvenosti (možda se grdno varam). Tada sfera ne bi bila ni 2-čelija.
Moj vam je savjet da se držite intuicije.  Znači, rub je ono gdje se možete porezati. Znači, rub je ono gdje se možete porezati. 
|
|
| [Vrh] |
|
Joker
Forumaš(ica)

Pridružen/a: 19. 09. 2010. (10:19:16)
Postovi: (8C)16
Spol: 
|
 Postano: 16:49 pon, 4. 6. 2012 Naslov: Postano: 16:49 pon, 4. 6. 2012 Naslov: |
    |
|
|
[quote="ceps"]http://web.math.pmf.unizg.hr/nastava/difraf/int/pred/p_o21.pdf
Na vrhu zadnje stranice ti piše kako se definira jedinična normala. Tebi u ovom zadatku normala ne treba biti jedinična (kažu da mora biti oblika [latex]c(1,1,1)[/latex] ), pa možeš zanemariti ovo dijeljenje normom.
Ti trebaš ''namjestiti'' parametrizaciju tako da bude pravilno orijentirana. Napiši si na početku parametrizaciju kakvu god hoćeš, dobit ćeš normalu oblika [latex]c(1,1,1)[/latex] ili [latex]-c(1,1,1)[/latex].
Ako je ovaj prvi oblik, super. Ako dobiješ ovaj drugi, trebaš samo ''promijeniti smjer'' (promijeniti orijentaciju) parametrizacije.
Javi ako zapneš negdje.[/quote]
...pa ako ti se da,jel bi mogao to raspisat,nisam sigurna bas u to :-/
| ceps (napisa): | http://web.math.pmf.unizg.hr/nastava/difraf/int/pred/p_o21.pdf
Na vrhu zadnje stranice ti piše kako se definira jedinična normala. Tebi u ovom zadatku normala ne treba biti jedinična (kažu da mora biti oblika 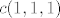 ), pa možeš zanemariti ovo dijeljenje normom. ), pa možeš zanemariti ovo dijeljenje normom.
Ti trebaš ''namjestiti'' parametrizaciju tako da bude pravilno orijentirana. Napiši si na početku parametrizaciju kakvu god hoćeš, dobit ćeš normalu oblika 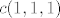 ili ili 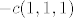 . .
Ako je ovaj prvi oblik, super. Ako dobiješ ovaj drugi, trebaš samo ''promijeniti smjer'' (promijeniti orijentaciju) parametrizacije.
Javi ako zapneš negdje. |
...pa ako ti se da,jel bi mogao to raspisat,nisam sigurna bas u to :-/
|
|
| [Vrh] |
|
satja
Forumaš(ica)

Pridružen/a: 16. 05. 2010. (10:44:17)
Postovi: (F1)16
|
 Postano: 17:10 pon, 4. 6. 2012 Naslov: Postano: 17:10 pon, 4. 6. 2012 Naslov: |
    |
|
|
@Joker: jedna moguca parametrizacija je [tex]\varphi(u,v) = (u, v, 1-u-v)[/tex], za [tex](u,v)[/tex] iz trokuta u [tex]\mathbb{R}^2[/tex] s vrhovima [tex](0,0), (0,1), (1,0)[/tex].
Edit: Rješenje ispadne 1/6.
@Joker: jedna moguca parametrizacija je [tex]\varphi(u,v) = (u, v, 1-u-v)[/tex], za [tex](u,v)[/tex] iz trokuta u [tex]\mathbb{R}^2[/tex] s vrhovima [tex](0,0), (0,1), (1,0)[/tex].
Edit: Rješenje ispadne 1/6.
|
|
| [Vrh] |
|
kikzmyster
Forumaš(ica)

Pridružen/a: 14. 10. 2010. (13:35:08)
Postovi: (72)16
Spol: 
|
|
| [Vrh] |
|
pmli
Forumaš(ica)

Pridružen/a: 09. 11. 2009. (12:03:05)
Postovi: (2C8)16
Spol: 
|
 Postano: 19:10 pon, 4. 6. 2012 Naslov: Postano: 19:10 pon, 4. 6. 2012 Naslov: |
    |
|
|
Probaj sam. Ima hrpe pisanja, ali samo koristiš definiciju integrala diferencijalne 1-forme. Jedina "fora" je ta da, ako s [latex]\gamma_1, \ldots, \gamma_4[/latex] parametriziraš stranice jediničnog kvadrata, sa [latex]\gamma_1 + \ldots + \gamma_4[/latex] si parametrizirao [latex]\partial I^2[/latex], a sa [latex]F \circ \gamma_1 + \ldots + F \circ \gamma_4[/latex] si onda parametrizirao [latex]\partial D[/latex].
Probaj sam. Ima hrpe pisanja, ali samo koristiš definiciju integrala diferencijalne 1-forme. Jedina "fora" je ta da, ako s 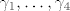 parametriziraš stranice jediničnog kvadrata, sa parametriziraš stranice jediničnog kvadrata, sa  si parametrizirao si parametrizirao 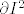 , a sa , a sa  si onda parametrizirao si onda parametrizirao 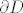 . .
|
|
| [Vrh] |
|
pmli
Forumaš(ica)

Pridružen/a: 09. 11. 2009. (12:03:05)
Postovi: (2C8)16
Spol: 
|
|
| [Vrh] |
|
jabuka
Forumaš(ica)
Pridružen/a: 21. 11. 2009. (15:53:14)
Postovi: (7C)16
|
|
| [Vrh] |
|
pmli
Forumaš(ica)

Pridružen/a: 09. 11. 2009. (12:03:05)
Postovi: (2C8)16
Spol: 
|
|
| [Vrh] |
|
ceps
Forumaš(ica)

Pridružen/a: 08. 10. 2010. (13:03:07)
Postovi: (13A)16
|
|
| [Vrh] |
|
pmli
Forumaš(ica)

Pridružen/a: 09. 11. 2009. (12:03:05)
Postovi: (2C8)16
Spol: 
|
|
| [Vrh] |
|
yellow submarine
Forumaš(ica)


Pridružen/a: 01. 10. 2010. (19:28:03)
Postovi: (34)16
Spol: 
|
|
| [Vrh] |
|
kiwi
Forumaš(ica)

Pridružen/a: 05. 06. 2012. (00:48:44)
Postovi: (1)16
|
|
| [Vrh] |
|
kobila krsto
Forumaš(ica)
Pridružen/a: 02. 07. 2009. (16:55:08)
Postovi: (6A)16
|
 Postano: 2:22 uto, 5. 6. 2012 Naslov: Postano: 2:22 uto, 5. 6. 2012 Naslov: |
    |
|
|
[quote="kikzmyster"]Napisi ovaj integral kao [tex]\int_\gamma(e^x\sin y + y)\, dx + (e^x\cos y + x)\, dy - \int_\gamma 3y \,dx [/tex]. Sad se prvi integral lako dobije, jer je potencijal podintegralne funkcije [tex]e^x \sin y + xy [/tex], a drugi integral isto izgleda lagan 8)[/quote]
zar ovo nije lakše preko greena samo ? :)
EDIT : @ kiwi ja bi tu provjerio je li omega zatvorena ( jest ) i pokazao da nije egzaktna ( da integral bude != 0 ) i dobije se integral 2pi kad parametriziraš kružnicu. b) dio uradiš ko na vježbama onaj dio s elipsom ;)
argumentiraš ono da nitegral ne ovisi o putu integracije pa ti valjda isto ispadne ( jer su oba područja na koja rastavimo kardioidu 1-povezana ). samo ne znam je li ovo po definiciji pa ako nije nek me neko ispravi jer onda i mene zanima :)
| kikzmyster (napisa): | Napisi ovaj integral kao [tex]\int_\gamma(e^x\sin y + y)\, dx + (e^x\cos y + x)\, dy - \int_\gamma 3y \,dx [/tex]. Sad se prvi integral lako dobije, jer je potencijal podintegralne funkcije [tex]e^x \sin y + xy [/tex], a drugi integral isto izgleda lagan  |
zar ovo nije lakše preko greena samo ? 
EDIT : @ kiwi ja bi tu provjerio je li omega zatvorena ( jest ) i pokazao da nije egzaktna ( da integral bude != 0 ) i dobije se integral 2pi kad parametriziraš kružnicu. b) dio uradiš ko na vježbama onaj dio s elipsom 
argumentiraš ono da nitegral ne ovisi o putu integracije pa ti valjda isto ispadne ( jer su oba područja na koja rastavimo kardioidu 1-povezana ). samo ne znam je li ovo po definiciji pa ako nije nek me neko ispravi jer onda i mene zanima 
|
|
| [Vrh] |
|
jabuka
Forumaš(ica)
Pridružen/a: 21. 11. 2009. (15:53:14)
Postovi: (7C)16
|
|
| [Vrh] |
|
rimidalv1991
Forumaš(ica)

Pridružen/a: 07. 07. 2009. (21:14:20)
Postovi: (22)16
|
 Postano: 8:58 uto, 5. 6. 2012 Naslov: Postano: 8:58 uto, 5. 6. 2012 Naslov: |
    |
|
|
[quote="jabuka"]moze pomoc? 7.a
http://web.math.pmf.unizg.hr/nastava/difraf/int/2007-08/IFVVkol2_2008.pdf[/quote]
Vrijedi ti z=f(x,y), i sad koristis parametrizaciju F(x,y)=(x,y,f(x,y)) i dalje ides po formuli.
Vrijedi ti z=f(x,y), i sad koristis parametrizaciju F(x,y)=(x,y,f(x,y)) i dalje ides po formuli.
|
|
| [Vrh] |
|
|














