| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
komaPMF
Forumaš(ica)


Pridružen/a: 22. 11. 2007. (10:23:41)
Postovi: (E6)16
Spol: 
Lokacija: Over the roof
|
|
| [Vrh] |
|
eve
Forumaš(ica)

Pridružen/a: 13. 07. 2009. (23:07:06)
Postovi: (192)16
Spol: 
|
|
| [Vrh] |
|
komaPMF
Forumaš(ica)


Pridružen/a: 22. 11. 2007. (10:23:41)
Postovi: (E6)16
Spol: 
Lokacija: Over the roof
|
|
| [Vrh] |
|
ivaa
Forumaš(ica)
Pridružen/a: 10. 07. 2009. (17:39:10)
Postovi: (7)16
|
|
| [Vrh] |
|
pmli
Forumaš(ica)

Pridružen/a: 09. 11. 2009. (12:03:05)
Postovi: (2C8)16
Spol: 
|
 Postano: 15:50 pon, 4. 6. 2012 Naslov: Postano: 15:50 pon, 4. 6. 2012 Naslov: |
    |
|
|
[quote="komaPMF"]Može li mi netko objasniti princip transfinitne indukcije, odnosno zašto to vrijedi ako uzmemo da je [latex]A=\mathbb{Z}[/latex], a [latex]B=2\mathbb{Z}[/latex]? U skripti piše da je za njih ispunjen uvjet [latex]( \forall x \in \mathbb{Z})(p_{\mathbb{Z}}(x)\subseteq 2\mahbb{}Z \Rightarrow x\in 2\mathbb{Z})[/latex], a nijedan početni komad od [latex]\mathbb{Z}[/latex] neće biti podskup od [latex]2\mathbb{Z}[/latex][/quote]
U tome je i stvar. :D Ne može vrijediti [latex]p_{\mathbb{Z}}(x) \subseteq 2 \mathbb{Z}[/latex], pa je implikacija uvijek točna. Dakle, vrijedi [latex]( \forall \, x \in \mathbb{Z})(p_{\mathbb{Z}}(x) \subseteq 2 \mathbb{Z} \Rightarrow x \in 2 \mathbb{Z})[/latex] i [latex]B \neq A[/latex], pa za skup [latex]A[/latex] ne vrijedi princip matematičke indukcije.
| komaPMF (napisa): | Može li mi netko objasniti princip transfinitne indukcije, odnosno zašto to vrijedi ako uzmemo da je  , a , a 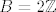 ? U skripti piše da je za njih ispunjen uvjet ? U skripti piše da je za njih ispunjen uvjet  , a nijedan početni komad od , a nijedan početni komad od 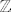 neće biti podskup od neće biti podskup od  |
U tome je i stvar.  Ne može vrijediti Ne može vrijediti 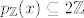 , pa je implikacija uvijek točna. Dakle, vrijedi , pa je implikacija uvijek točna. Dakle, vrijedi  i i 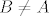 , pa za skup , pa za skup  ne vrijedi princip matematičke indukcije. ne vrijedi princip matematičke indukcije.
|
|
| [Vrh] |
|
komaPMF
Forumaš(ica)


Pridružen/a: 22. 11. 2007. (10:23:41)
Postovi: (E6)16
Spol: 
Lokacija: Over the roof
|
|
| [Vrh] |
|
heidi75
Forumaš(ica)
Pridružen/a: 18. 02. 2009. (21:51:01)
Postovi: (8)16
|
|
| [Vrh] |
|
pmli
Forumaš(ica)

Pridružen/a: 09. 11. 2009. (12:03:05)
Postovi: (2C8)16
Spol: 
|
 Postano: 17:34 pon, 4. 6. 2012 Naslov: Postano: 17:34 pon, 4. 6. 2012 Naslov: |
    |
|
|
[quote="ivaa"]Jel bi mogao netko raspisat zadnji zadatak s prošlogodišnjeg kolokvija, onaj sa Zornovom lemom? Hvala[/quote]
Treba pokazati da [dtex](\{S \subseteq \mathbb{R} \times \mathbb{C} \mid S \neq \emptyset,\ (\forall \, (x_1, z_1), (x_2, z_2) \in S)((x_1 + x_2, z_1 + z_2) \in S),\ S \cap (\mathbb{Q} \times \mathbb{C}) = \emptyset,\ S \cap (\mathbb{R} \times \mathbb{R}) = \emptyset\}, \subset)[/dtex] ima maksimalni element. To je standardni zadatak s vježbi. Uzmemo proizvoljni lanac [tex]\mathcal{C}[/tex]. Ako je prazan, onda je [tex]\{(n \sqrt{2}, mi) \mid n, m \in \mathbb{N} \setminus \{0\}\}[/tex] neka njegova gornja međa. Ako je neprazan, pokaže se da je unija svih elemenata lanca gornja međa.
Reci ako nešto treba detaljnije objasniti.
[quote="heidi75"]jel moze netko rijesit ili bar napisat ideju za 6. zad od prosle godine????? :?[/quote]
Imaš rješenje u zbirci (zadatak 221.).
| ivaa (napisa): | | Jel bi mogao netko raspisat zadnji zadatak s prošlogodišnjeg kolokvija, onaj sa Zornovom lemom? Hvala |
Treba pokazati da [dtex](\{S \subseteq \mathbb{R} \times \mathbb{C} \mid S \neq \emptyset,\ (\forall \, (x_1, z_1), (x_2, z_2) \in S)((x_1 + x_2, z_1 + z_2) \in S),\ S \cap (\mathbb{Q} \times \mathbb{C}) = \emptyset,\ S \cap (\mathbb{R} \times \mathbb{R}) = \emptyset\}, \subset)[/dtex] ima maksimalni element. To je standardni zadatak s vježbi. Uzmemo proizvoljni lanac [tex]\mathcal{C}[/tex]. Ako je prazan, onda je [tex]\{(n \sqrt{2}, mi) \mid n, m \in \mathbb{N} \setminus \{0\}\}[/tex] neka njegova gornja međa. Ako je neprazan, pokaže se da je unija svih elemenata lanca gornja međa.
Reci ako nešto treba detaljnije objasniti.
| heidi75 (napisa): | jel moze netko rijesit ili bar napisat ideju za 6. zad od prosle godine?????  |
Imaš rješenje u zbirci (zadatak 221.).
|
|
| [Vrh] |
|
heidi75
Forumaš(ica)
Pridružen/a: 18. 02. 2009. (21:51:01)
Postovi: (8)16
|
|
| [Vrh] |
|
pmli
Forumaš(ica)

Pridružen/a: 09. 11. 2009. (12:03:05)
Postovi: (2C8)16
Spol: 
|
|
| [Vrh] |
|
heidi75
Forumaš(ica)
Pridružen/a: 18. 02. 2009. (21:51:01)
Postovi: (8)16
|
|
| [Vrh] |
|
bbanelli
Forumaš(ica)
Pridružen/a: 16. 03. 2011. (09:21:40)
Postovi: (2C)16
Lokacija: Zagreb
|
 Postano: 9:58 uto, 5. 6. 2012 Naslov: Postano: 9:58 uto, 5. 6. 2012 Naslov: |
    |
|
|
[quote="mdoko"][quote="weirdie"]
ne znam jel u meni stvar ili u linku, ali mi se ne otvaraju rezultati prvog klk.
moze li netko pliz stavit link ovdje na forum?[/quote]
[url=https://docs.google.com/spreadsheet/pub?key=0ArlWKZO8hXUGdFZwUFcyd25Da1I3Z1FDWUJTa0xPX0E&single=true&gid=6&output=pdf]Može.[/url][/quote]Moze neka alternativna lokacija rezultata prvog kolokvija, ovo ne radi nazalost. :(
| mdoko (napisa): | | weirdie (napisa): |
ne znam jel u meni stvar ili u linku, ali mi se ne otvaraju rezultati prvog klk.
moze li netko pliz stavit link ovdje na forum? |
Može. |
Moze neka alternativna lokacija rezultata prvog kolokvija, ovo ne radi nazalost. 
_________________ Matematika
Dijeli ljude na dvije grupe. One kojima nije jasna i one kojima nije jasno kako ovim prvima nije jasna.
§ https://www.pci-z.com/ § |
|
| [Vrh] |
|
mdoko
Forumaš(ica)


Pridružen/a: 30. 11. 2002. (22:17:12)
Postovi: (71A)16
Spol: 
Lokacija: Heriot-Watt University, Edinburgh
|
|
| [Vrh] |
|
nuala
Forumaš(ica)

Pridružen/a: 20. 02. 2011. (14:26:29)
Postovi: (33)16
|
|
| [Vrh] |
|
smajl
Forumaš(ica)

Pridružen/a: 02. 01. 2010. (12:59:23)
Postovi: (EB)16
Spol: 
Lokacija: Zagreb
|
|
| [Vrh] |
|
-student-
Forumaš(ica)

Pridružen/a: 13. 09. 2010. (22:52:43)
Postovi: (C)16
|
|
| [Vrh] |
|
mdoko
Forumaš(ica)


Pridružen/a: 30. 11. 2002. (22:17:12)
Postovi: (71A)16
Spol: 
Lokacija: Heriot-Watt University, Edinburgh
|
|
| [Vrh] |
|
irena0102
Forumaš(ica)


Pridružen/a: 01. 02. 2010. (11:49:52)
Postovi: (45)16
Spol: 
|
|
| [Vrh] |
|
vancika
Forumaš(ica)


Pridružen/a: 08. 07. 2007. (20:11:36)
Postovi: (92)16
Lokacija: Varaždin
|
|
| [Vrh] |
|
slon
Forumaš(ica)

Pridružen/a: 10. 02. 2009. (20:10:11)
Postovi: (F)16
|
|
| [Vrh] |
|
|















