| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
coco88
Forumaš(ica)

Pridružen/a: 11. 11. 2010. (16:00:09)
Postovi: (10)16
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
:/
Gost
|
|
| [Vrh] |
|
čungalunga
Forumaš(ica)


Pridružen/a: 25. 11. 2009. (20:50:12)
Postovi: (4C)16
Spol: 
Lokacija: varaždin/zagreb
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
pmli
Forumaš(ica)

Pridružen/a: 09. 11. 2009. (12:03:05)
Postovi: (2C8)16
Spol: 
|
 Postano: 10:20 sub, 9. 6. 2012 Naslov: Postano: 10:20 sub, 9. 6. 2012 Naslov: |
    |
|
|
[quote="čungalunga"]jel bi netko mogao pliz riješiti 2. i 3. zadatak iz ovogodišnjeg drugog kolokvija?
http://web.math.pmf.unizg.hr/nastava/mmf/kolokviji/mmf2kol2012.pdf[/quote]
2. Promatramo zadaću koji znamo riješiti:
[tex]\begin{align}
\tilde{u}_t & = \tilde{u}_{xx} \textrm{ u } \mathbb{R} \times \mathbb{R}^+ \\
\tilde{u}(x, 0) & = \tilde{u}_0(x)
\end{align}[/tex]
Vrijedit će ista PDJ kao za zadaću iz zadatka (jej!), tražimo da vrijedi [tex]\tilde{u}(x, 0) = u(x, 0)[/tex] za [tex]x > 0[/tex], tj. [tex]\tilde{u}_0(x) = u_0(x)[/tex] za [tex]x > 0[/tex], te [tex]\tilde{u}_x(0, t) = 0[/tex]. Ono što nam je nepoznato su vrijednosti [tex]\tilde{u}_0(x)[/tex] za [tex]x < 0[/tex], pa se to nadamo izvući iz [tex]\tilde{u}_x(0, t) = 0[/tex].
To je u biti to. Treba sad raspisati taj rubni uvjet, znači ubaciti Poissonovu formulu, derivirati po [tex]x[/tex], uvrstiti [tex]x = 0[/tex], izjednačiti to s [tex]0[/tex], rastaviti integrale na pozitivni i negativni dio ([tex]\int\limits_{-\infty}^{+\infty} = \int\limits_{-\infty}^{0} + \int\limits_{0}^{+\infty}[/tex]), supstituciju napraviti... Uglavnom, kao na vježbama taj sličan zadatak.
Dobi se da će biti ok ako se parno proširi, tj. [latex]\tilde{u}_0(-x) = \tilde{u}_0(x)[/latex], za [tex]x > 0[/tex].
3. Prvo supstitucija [tex]u(x, t) = v(x, t) + \varphi(x)[/tex] da dobimo homogene uvjete (ispadne [tex]\varphi(x) = x + 1[/tex]). Zatim možemo primijeniti metodu separacije varijable na homogenu jednadžbu za [tex]v[/tex] da dobimo [latex]\lambda_k[/latex] i [tex]X_k[/tex] ([tex]k \in \mathbb{N}[/tex]). Zatim za cijeli [tex]v[/tex] tražimo rješenje oblika [tex]\displaystyle \sum_{k = 1}^{\infty} T_k(t) X_k(x)[/tex]. To uvrstiš u PDJ, dobiš ODJ za [tex]T_k[/tex]...
Ako treba još, reci.
2. Promatramo zadaću koji znamo riješiti:
[tex]\begin{align}
\tilde{u}_t & = \tilde{u}_{xx} \textrm{ u } \mathbb{R} \times \mathbb{R}^+ \\
\tilde{u}(x, 0) & = \tilde{u}_0(x)
\end{align}[/tex]
Vrijedit će ista PDJ kao za zadaću iz zadatka (jej!), tražimo da vrijedi [tex]\tilde{u}(x, 0) = u(x, 0)[/tex] za [tex]x > 0[/tex], tj. [tex]\tilde{u}_0(x) = u_0(x)[/tex] za [tex]x > 0[/tex], te [tex]\tilde{u}_x(0, t) = 0[/tex]. Ono što nam je nepoznato su vrijednosti [tex]\tilde{u}_0(x)[/tex] za [tex]x < 0[/tex], pa se to nadamo izvući iz [tex]\tilde{u}_x(0, t) = 0[/tex].
To je u biti to. Treba sad raspisati taj rubni uvjet, znači ubaciti Poissonovu formulu, derivirati po [tex]x[/tex], uvrstiti [tex]x = 0[/tex], izjednačiti to s [tex]0[/tex], rastaviti integrale na pozitivni i negativni dio ([tex]\int\limits_{-\infty}^{+\infty} = \int\limits_{-\infty}^{0} + \int\limits_{0}^{+\infty}[/tex]), supstituciju napraviti... Uglavnom, kao na vježbama taj sličan zadatak.
Dobi se da će biti ok ako se parno proširi, tj. 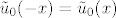 , za [tex]x > 0[/tex]. , za [tex]x > 0[/tex].
3. Prvo supstitucija [tex]u(x, t) = v(x, t) + \varphi(x)[/tex] da dobimo homogene uvjete (ispadne [tex]\varphi(x) = x + 1[/tex]). Zatim možemo primijeniti metodu separacije varijable na homogenu jednadžbu za [tex]v[/tex] da dobimo 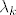 i [tex]X_k[/tex] ([tex]k \in \mathbb{N}[/tex]). Zatim za cijeli [tex]v[/tex] tražimo rješenje oblika [tex]\displaystyle \sum_{k = 1}^{\infty} T_k(t) X_k(x)[/tex]. To uvrstiš u PDJ, dobiš ODJ za [tex]T_k[/tex]... i [tex]X_k[/tex] ([tex]k \in \mathbb{N}[/tex]). Zatim za cijeli [tex]v[/tex] tražimo rješenje oblika [tex]\displaystyle \sum_{k = 1}^{\infty} T_k(t) X_k(x)[/tex]. To uvrstiš u PDJ, dobiš ODJ za [tex]T_k[/tex]...
Ako treba još, reci.
|
|
| [Vrh] |
|
Genaro
Forumaš(ica)

Pridružen/a: 27. 10. 2009. (18:57:50)
Postovi: (8B)16
Spol: 
Lokacija: Zagreb
|
|
| [Vrh] |
|
pmli
Forumaš(ica)

Pridružen/a: 09. 11. 2009. (12:03:05)
Postovi: (2C8)16
Spol: 
|
 Postano: 15:35 sub, 9. 6. 2012 Naslov: Postano: 15:35 sub, 9. 6. 2012 Naslov: |
    |
|
|
[quote="Genaro"]Ako može, malo pomoći oko principa rješavanja 5. zadatka sa tog istog kolokvija?[/quote]
Koristi se Dirichletov teorem i teorem o uniformnoj konvergenciji Fourierovog reda (nismo mu nadjenuli neko ime, ovo je tek tolko da se lakše referiram). U oba se spominju "po dijelovima neprekidne funkcije":
[i]Kažemo da je [tex]f[/tex] po dijelovima neprekidna na [tex][a, b][/tex] ako je:
1) [tex]f[/tex] definirana na [tex][a, b][/tex] osim u konačno mnogo točaka,
2) [tex]f[/tex] neprekidna svuda gdje je definirana, osim u konačno mnogo točaka
3) u točkama prekida [tex]f[/tex] ima limese slijeva i zdesna. Pišemo [tex]f(x-) := \lim\limits_{t \nearrow x} f(t)[/tex], [tex]f(x+) := \lim\limits_{t \searrow x} f(t)[/tex].[/i]
Trigonometrijski Fourierov red je [dtex]\frac{a_0}{2} + \sum_{k = 0}^{\infty}\left(a_k \cos\frac{k \pi x}{L} + b_k \sin\frac{k \pi x}{L} \right), \quad (*)[/dtex] gdje je [dtex]a_k = \frac{1}{L} \int\limits_{-L}^L{f(x) \cos\frac{k \pi x}{L} dx}\ \textrm{ i }\ b_k = \frac{1}{L} \int\limits_{-L}^L{f(x) \sin\frac{k \pi x}{L} dx}[/dtex]
Iskaz Dirichletovog teorema:
[i]Neka je [tex]f[/tex] po dijelovima neprekidna na [tex][-L, L][/tex] takva da je i [tex]f'[/tex] po dijelovima neprekidna na [tex][-L, L][/tex]. Tada red [tex](*)[/tex] konvergira prema [tex]f(x)[/tex] u svim točkama [tex]x[/tex] u kojima je [tex]f[/tex] neprekidna. U točkama prekida funkcije [tex]f[/tex] red [tex](*)[/tex] konvergira prema [tex]\frac{f(x-) + f(x+)}{2}[/tex].[/i]
To kaže da [tex](*)[/tex] konvergira po točkama, i gdje točno konvergira. Podrazumijeva se da je [tex]f[/tex] proširena po periodičnosti (da bi imali smisla ovi limesi na rubovima).
Sad ovaj drugi teorem, o uniformnoj konvergenciji. Ono što je fora je da se pretpostavkama Dirichletovog teorema treba dodati samo ono što je nužno, a to je da je [tex]f[/tex] neprekidna kad se proširi po periodičnosti.
[i]Neka je [tex]f[/tex] neprekidna na [tex][-L, L][/tex], [tex]f'[/tex] po dijelovima neprekidna na [tex][-L, L][/tex] i [tex]f(-L) = f(L)[/tex]. Tada [tex](*)[/tex] konvergira uniformno prema [tex]f[/tex] na [tex][-L, L][/tex].[/i]
Kad se govori o Fourierovom redu po sinusima funkcije [tex]f[/tex] definirane na [tex][0, L][/tex], misli se na Fourierov red od neparnog proširenja na [tex][-L, L][/tex] (tada je [tex]a_k = 0[/tex]). Za uniformu konvergenciju je potrebno provjeriti (uz neprekidnost od [tex]f[/tex] i po dijelovima neprekidnost od [tex]f'[/tex]) da je [tex]f(0) = f(L) = 0[/tex] (nacrtaj sliku).
Slično se može gledati i Fourierov red po kosinusima, samo se gleda parno proširenje. Ovdje je bolja situacija u tome što je dovoljno provjeriti neprekidnost od [tex]f[/tex] i po dijelovima neprekidnost od [tex]f'[/tex] (slika).
| Genaro (napisa): | | Ako može, malo pomoći oko principa rješavanja 5. zadatka sa tog istog kolokvija? |
Koristi se Dirichletov teorem i teorem o uniformnoj konvergenciji Fourierovog reda (nismo mu nadjenuli neko ime, ovo je tek tolko da se lakše referiram). U oba se spominju "po dijelovima neprekidne funkcije":
Kažemo da je [tex]f[/tex] po dijelovima neprekidna na [tex][a, b][/tex] ako je:
1) [tex]f[/tex] definirana na [tex][a, b][/tex] osim u konačno mnogo točaka,
2) [tex]f[/tex] neprekidna svuda gdje je definirana, osim u konačno mnogo točaka
3) u točkama prekida [tex]f[/tex] ima limese slijeva i zdesna. Pišemo [tex]f(x-) := \lim\limits_{t \nearrow x} f(t)[/tex], [tex]f(x+) := \lim\limits_{t \searrow x} f(t)[/tex].
Trigonometrijski Fourierov red je [dtex]\frac{a_0}{2} + \sum_{k = 0}^{\infty}\left(a_k \cos\frac{k \pi x}{L} + b_k \sin\frac{k \pi x}{L} \right), \quad (*)[/dtex] gdje je [dtex]a_k = \frac{1}{L} \int\limits_{-L}^L{f(x) \cos\frac{k \pi x}{L} dx}\ \textrm{ i }\ b_k = \frac{1}{L} \int\limits_{-L}^L{f(x) \sin\frac{k \pi x}{L} dx}[/dtex]
Iskaz Dirichletovog teorema:
Neka je [tex]f[/tex] po dijelovima neprekidna na [tex][-L, L][/tex] takva da je i [tex]f'[/tex] po dijelovima neprekidna na [tex][-L, L][/tex]. Tada red [tex](*)[/tex] konvergira prema [tex]f(x)[/tex] u svim točkama [tex]x[/tex] u kojima je [tex]f[/tex] neprekidna. U točkama prekida funkcije [tex]f[/tex] red [tex](*)[/tex] konvergira prema [tex]\frac{f(x-) + f(x+)}{2}[/tex].
To kaže da [tex](*)[/tex] konvergira po točkama, i gdje točno konvergira. Podrazumijeva se da je [tex]f[/tex] proširena po periodičnosti (da bi imali smisla ovi limesi na rubovima).
Sad ovaj drugi teorem, o uniformnoj konvergenciji. Ono što je fora je da se pretpostavkama Dirichletovog teorema treba dodati samo ono što je nužno, a to je da je [tex]f[/tex] neprekidna kad se proširi po periodičnosti.
Neka je [tex]f[/tex] neprekidna na [tex][-L, L][/tex], [tex]f'[/tex] po dijelovima neprekidna na [tex][-L, L][/tex] i [tex]f(-L) = f(L)[/tex]. Tada [tex](*)[/tex] konvergira uniformno prema [tex]f[/tex] na [tex][-L, L][/tex].
Kad se govori o Fourierovom redu po sinusima funkcije [tex]f[/tex] definirane na [tex][0, L][/tex], misli se na Fourierov red od neparnog proširenja na [tex][-L, L][/tex] (tada je [tex]a_k = 0[/tex]). Za uniformu konvergenciju je potrebno provjeriti (uz neprekidnost od [tex]f[/tex] i po dijelovima neprekidnost od [tex]f'[/tex]) da je [tex]f(0) = f(L) = 0[/tex] (nacrtaj sliku).
Slično se može gledati i Fourierov red po kosinusima, samo se gleda parno proširenje. Ovdje je bolja situacija u tome što je dovoljno provjeriti neprekidnost od [tex]f[/tex] i po dijelovima neprekidnost od [tex]f'[/tex] (slika).
|
|
| [Vrh] |
|
Genaro
Forumaš(ica)

Pridružen/a: 27. 10. 2009. (18:57:50)
Postovi: (8B)16
Spol: 
Lokacija: Zagreb
|
|
| [Vrh] |
|
Megy Poe
Forumaš(ica)

Pridružen/a: 05. 11. 2009. (23:14:52)
Postovi: (122)16
|
 Postano: 23:02 sub, 9. 6. 2012 Naslov: Postano: 23:02 sub, 9. 6. 2012 Naslov: |
    |
|
|
[quote="pmli"][quote="čungalunga"]jel bi netko mogao pliz riješiti 2. i 3. zadatak iz ovogodišnjeg drugog kolokvija?
http://web.math.pmf.unizg.hr/nastava/mmf/kolokviji/mmf2kol2012.pdf[/quote]
2. Promatramo zadaću koji znamo riješiti:
[tex]\begin{align}
\tilde{u}_t & = \tilde{u}_{xx} \textrm{ u } \mathbb{R} \times \mathbb{R}^+ \\
\tilde{u}(x, 0) & = \tilde{u}_0(x)
\end{align}[/tex]
Vrijedit će ista PDJ kao za zadaću iz zadatka (jej!), tražimo da vrijedi [tex]\tilde{u}(x, 0) = u(x, 0)[/tex] za [tex]x > 0[/tex], tj. [tex]\tilde{u}_0(x) = u_0(x)[/tex] za [tex]x > 0[/tex], te [tex]\tilde{u}_x(0, t) = 0[/tex]. Ono što nam je nepoznato su vrijednosti [tex]\tilde{u}_0(x)[/tex] za [tex]x < 0[/tex], pa se to nadamo izvući iz [tex]\tilde{u}_x(0, t) = 0[/tex].
To je u biti to. Treba sad raspisati taj rubni uvjet, znači ubaciti Poissonovu formulu, derivirati po [tex]x[/tex], uvrstiti [tex]x = 0[/tex], izjednačiti to s [tex]0[/tex], rastaviti integrale na pozitivni i negativni dio ([tex]\int\limits_{-\infty}^{+\infty} = \int\limits_{-\infty}^{0} + \int\limits_{0}^{+\infty}[/tex]), supstituciju napraviti... Uglavnom, kao na vježbama taj sličan zadatak.
Dobi se da će biti ok ako se parno proširi, tj. [latex]\tilde{u}_0(-x) = \tilde{u}_0(x)[/latex], za [tex]x > 0[/tex].
3. Prvo supstitucija [tex]u(x, t) = v(x, t) + \varphi(x)[/tex] da dobimo homogene uvjete (ispadne [tex]\varphi(x) = x + 1[/tex]). Zatim možemo primijeniti metodu separacije varijable na homogenu jednadžbu za [tex]v[/tex] da dobimo [latex]\lambda_k[/latex] i [tex]X_k[/tex] ([tex]k \in \mathbb{N}[/tex]). Zatim za cijeli [tex]v[/tex] tražimo rješenje oblika [tex]\displaystyle \sum_{k = 1}^{\infty} T_k(t) X_k(x)[/tex]. To uvrstiš u PDJ, dobiš ODJ za [tex]T_k[/tex]...
Ako treba još, reci.[/quote]
Ja bi samo htjela provjeriti da li sam ja to dobro do kraja jel baš nisam sigurna kad treba tražiti T...Da li dobijemo rješenja [latex]\lambda[/latex]=1 i [latex]\lambda[/latex]=2...pa je rješenje cos[latex]\pi[/latex]t*sin[latex]\pi[/latex]x-t^2sin[latex]\pi[/latex]x+ sin2[latex]\pi[/latex]t)*sin2[latex]\pi[/latex]x-t^2sin[latex]\pi[/latex]x
| pmli (napisa): |
2. Promatramo zadaću koji znamo riješiti:
[tex]\begin{align}
\tilde{u}_t & = \tilde{u}_{xx} \textrm{ u } \mathbb{R} \times \mathbb{R}^+ \\
\tilde{u}(x, 0) & = \tilde{u}_0(x)
\end{align}[/tex]
Vrijedit će ista PDJ kao za zadaću iz zadatka (jej!), tražimo da vrijedi [tex]\tilde{u}(x, 0) = u(x, 0)[/tex] za [tex]x > 0[/tex], tj. [tex]\tilde{u}_0(x) = u_0(x)[/tex] za [tex]x > 0[/tex], te [tex]\tilde{u}_x(0, t) = 0[/tex]. Ono što nam je nepoznato su vrijednosti [tex]\tilde{u}_0(x)[/tex] za [tex]x < 0[/tex], pa se to nadamo izvući iz [tex]\tilde{u}_x(0, t) = 0[/tex].
To je u biti to. Treba sad raspisati taj rubni uvjet, znači ubaciti Poissonovu formulu, derivirati po [tex]x[/tex], uvrstiti [tex]x = 0[/tex], izjednačiti to s [tex]0[/tex], rastaviti integrale na pozitivni i negativni dio ([tex]\int\limits_{-\infty}^{+\infty} = \int\limits_{-\infty}^{0} + \int\limits_{0}^{+\infty}[/tex]), supstituciju napraviti... Uglavnom, kao na vježbama taj sličan zadatak.
Dobi se da će biti ok ako se parno proširi, tj. 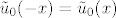 , za [tex]x > 0[/tex]. , za [tex]x > 0[/tex].
3. Prvo supstitucija [tex]u(x, t) = v(x, t) + \varphi(x)[/tex] da dobimo homogene uvjete (ispadne [tex]\varphi(x) = x + 1[/tex]). Zatim možemo primijeniti metodu separacije varijable na homogenu jednadžbu za [tex]v[/tex] da dobimo 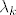 i [tex]X_k[/tex] ([tex]k \in \mathbb{N}[/tex]). Zatim za cijeli [tex]v[/tex] tražimo rješenje oblika [tex]\displaystyle \sum_{k = 1}^{\infty} T_k(t) X_k(x)[/tex]. To uvrstiš u PDJ, dobiš ODJ za [tex]T_k[/tex]... i [tex]X_k[/tex] ([tex]k \in \mathbb{N}[/tex]). Zatim za cijeli [tex]v[/tex] tražimo rješenje oblika [tex]\displaystyle \sum_{k = 1}^{\infty} T_k(t) X_k(x)[/tex]. To uvrstiš u PDJ, dobiš ODJ za [tex]T_k[/tex]...
Ako treba još, reci. |
Ja bi samo htjela provjeriti da li sam ja to dobro do kraja jel baš nisam sigurna kad treba tražiti T...Da li dobijemo rješenja  =1 i =1 i  =2...pa je rješenje cos =2...pa je rješenje cos t*sin t*sin x-t^2sin x-t^2sin x+ sin2 x+ sin2 t)*sin2 t)*sin2 x-t^2sin x-t^2sin x x
|
|
| [Vrh] |
|
dragec
Forumaš(ica)

Pridružen/a: 23. 06. 2011. (00:58:35)
Postovi: (3)16
|
|
| [Vrh] |
|
Megy Poe
Forumaš(ica)

Pridružen/a: 05. 11. 2009. (23:14:52)
Postovi: (122)16
|
|
| [Vrh] |
|
Gost
|
 Postano: 5:41 ned, 10. 6. 2012 Naslov: Postano: 5:41 ned, 10. 6. 2012 Naslov: |
    |
|
|
[quote="Megy Poe"][quote="dragec"]ima li mozda neka dobra dusa kojoj bi se dalo raspisati kako se rjesava 5. zadatak ovdje
http://web.math.pmf.unizg.hr/nastava/mmf/kolokviji/mmf_kol1_0809.pdf
ili bilo koji drugi zadatak gdje se koristi bernoullijev princip[/quote]
Ne znam je li ponavljaš prvi kolokvij ili pišeš sve, u slučaju da pišeš sve teoretsko pitanje bit će iz PDJ-a, tj neće biti bernoullijevog prinicipa.[/quote]
Asistent Marohnić je rekao da će biti 5 zadataka (bez teorije) u popravnom kolokviju s cijelim gradivom. Poslao sam mu jučer mail pa mi je to odgovorio.
Što se tiče ove SL-zadaće iz drugog kolokvija, pitanje... Kad dobivamo X i T, što se dogodi sa t^2sin(pi*x)? Tj. nakon što homogeniziramo jednadžbu i raspisujemo v(x,t). Dobijemo XT'' = 2X''T + t^2sin(pi * x). Kako sad doći do -lambda? Pretpostavljam da je lako, ali slab sam sa ODJ :( Cijenio bih neku dobru dušu ako može malo raspisati zadatak...
| Megy Poe (napisa): |
Ne znam je li ponavljaš prvi kolokvij ili pišeš sve, u slučaju da pišeš sve teoretsko pitanje bit će iz PDJ-a, tj neće biti bernoullijevog prinicipa. |
Asistent Marohnić je rekao da će biti 5 zadataka (bez teorije) u popravnom kolokviju s cijelim gradivom. Poslao sam mu jučer mail pa mi je to odgovorio.
Što se tiče ove SL-zadaće iz drugog kolokvija, pitanje... Kad dobivamo X i T, što se dogodi sa t^2sin(pi*x)? Tj. nakon što homogeniziramo jednadžbu i raspisujemo v(x,t). Dobijemo XT'' = 2X''T + t^2sin(pi * x). Kako sad doći do -lambda? Pretpostavljam da je lako, ali slab sam sa ODJ  Cijenio bih neku dobru dušu ako može malo raspisati zadatak... Cijenio bih neku dobru dušu ako može malo raspisati zadatak...
|
|
| [Vrh] |
|
pmli
Forumaš(ica)

Pridružen/a: 09. 11. 2009. (12:03:05)
Postovi: (2C8)16
Spol: 
|
 Postano: 10:58 ned, 10. 6. 2012 Naslov: Postano: 10:58 ned, 10. 6. 2012 Naslov: |
    |
|
|
Ponovo 3.
Nakon supstitucije, dobimo početno-rubnu zadaću:
[dtex]\begin{align}
v_{tt} & = v_{xx} + t^2 \sin(\pi x) \ \textrm{ u } \ \langle 0, 1 \rangle \times \mathbb{R}^+ \\
v(x, 0) & = \sin(\pi x) \\
v_t(x, 0) & = \sin(2 \pi x) \\
v(0, t) & = 0 \\
v(1, t) & = 0
\end{align}[/dtex]
Na homogenu zadaću [dtex]\begin{align}
v_{tt}^H & = v_{xx}^H \ \textrm{ u } \ \langle 0, 1 \rangle \times \mathbb{R}^+ \\
v^H(x, 0) & = \sin(\pi x) \\
v_t^H(x, 0) & = \sin(2 \pi x) \\
v^H(0, t) & = 0 \\
v^H(1, t) & = 0
\end{align}[/dtex]primijenimo metodu separacije varijabli. Nakon malo igranja, dobimo Sturm-Liouvilleovu zadaću [dtex]X'' + \lambda X = 0,\ X(0) = X(1) = 0.[/dtex] Njeno rješenje je [dtex]\lambda_k = (k \pi)^2,\ X_k(x) = \sin(k \pi x),\ k \in \mathbb{N}.[/dtex] Sad tražimo rješenje oblika [dtex]\sum_{k = 1}^{\infty}{T_k(t) X_k(x)}[/dtex] za [tex]v[/tex]. Kad to uvrtimo u PDJ za [tex]v[/tex], dobimo (nakon deriviranja i prebacivanja) [dtex]\sum_{k = 1}^{\infty}\left(T''_k(t) + (k \pi)^2 T_k(t)\right)\sin(k \pi x) = t^2 \sin(\pi x).[/dtex] Primijetio da je s desne strane Fourierov red (koje li slučajnosti). Zato smijemo izjednačiti izraze uz [tex]\sin(k \pi x)[/tex] s obje strane. Tako dobimo ODJ [dtex]\begin{align}
T''_1(t) + \pi^2 T_1(t) & = t^2 \\
T''_k(t) + (k \pi)^2 T_k(t) & = 0 \ \textrm{ za } k \geq 2
\end{align}[/dtex]
Nastavit ću ako netko pita. Konačno rješenje je [dtex]u(x, t) = \frac{(\pi^4 + 2) \cos(\pi t) + \pi^2 t^2 - 2}{\pi^4} \sin(\pi x) + \frac{\sin(2 \pi t)}{2 \pi} \sin(2 \pi x) + x + 1.[/dtex]
Ponovo 3.
Nakon supstitucije, dobimo početno-rubnu zadaću:
[dtex]\begin{align}
v_{tt} & = v_{xx} + t^2 \sin(\pi x) \ \textrm{ u } \ \langle 0, 1 \rangle \times \mathbb{R}^+ \\
v(x, 0) & = \sin(\pi x) \\
v_t(x, 0) & = \sin(2 \pi x) \\
v(0, t) & = 0 \\
v(1, t) & = 0
\end{align}[/dtex]
Na homogenu zadaću [dtex]\begin{align}
v_{tt}^H & = v_{xx}^H \ \textrm{ u } \ \langle 0, 1 \rangle \times \mathbb{R}^+ \\
v^H(x, 0) & = \sin(\pi x) \\
v_t^H(x, 0) & = \sin(2 \pi x) \\
v^H(0, t) & = 0 \\
v^H(1, t) & = 0
\end{align}[/dtex]primijenimo metodu separacije varijabli. Nakon malo igranja, dobimo Sturm-Liouvilleovu zadaću [dtex]X'' + \lambda X = 0,\ X(0) = X(1) = 0.[/dtex] Njeno rješenje je [dtex]\lambda_k = (k \pi)^2,\ X_k(x) = \sin(k \pi x),\ k \in \mathbb{N}.[/dtex] Sad tražimo rješenje oblika [dtex]\sum_{k = 1}^{\infty}{T_k(t) X_k(x)}[/dtex] za [tex]v[/tex]. Kad to uvrtimo u PDJ za [tex]v[/tex], dobimo (nakon deriviranja i prebacivanja) [dtex]\sum_{k = 1}^{\infty}\left(T''_k(t) + (k \pi)^2 T_k(t)\right)\sin(k \pi x) = t^2 \sin(\pi x).[/dtex] Primijetio da je s desne strane Fourierov red (koje li slučajnosti). Zato smijemo izjednačiti izraze uz [tex]\sin(k \pi x)[/tex] s obje strane. Tako dobimo ODJ [dtex]\begin{align}
T''_1(t) + \pi^2 T_1(t) & = t^2 \\
T''_k(t) + (k \pi)^2 T_k(t) & = 0 \ \textrm{ za } k \geq 2
\end{align}[/dtex]
Nastavit ću ako netko pita. Konačno rješenje je [dtex]u(x, t) = \frac{(\pi^4 + 2) \cos(\pi t) + \pi^2 t^2 - 2}{\pi^4} \sin(\pi x) + \frac{\sin(2 \pi t)}{2 \pi} \sin(2 \pi x) + x + 1.[/dtex]
|
|
| [Vrh] |
|
Megy Poe
Forumaš(ica)

Pridružen/a: 05. 11. 2009. (23:14:52)
Postovi: (122)16
|
 Postano: 11:36 ned, 10. 6. 2012 Naslov: Postano: 11:36 ned, 10. 6. 2012 Naslov: |
    |
|
|
[quote="pmli"]Ponovo 3.
Nakon supstitucije, dobimo početno-rubnu zadaću:
[dtex]\begin{align}
v_{tt} & = v_{xx} + t^2 \sin(\pi x) \ \textrm{ u } \ \langle 0, 1 \rangle \times \mathbb{R}^+ \\
v(x, 0) & = \sin(\pi x) \\
v_t(x, 0) & = \sin(2 \pi x) \\
v(0, t) & = 0 \\
v(1, t) & = 0
\end{align}[/dtex]
Na homogenu zadaću [dtex]\begin{align}
v_{tt}^H & = v_{xx}^H \ \textrm{ u } \ \langle 0, 1 \rangle \times \mathbb{R}^+ \\
v^H(x, 0) & = \sin(\pi x) \\
v_t^H(x, 0) & = \sin(2 \pi x) \\
v^H(0, t) & = 0 \\
v^H(1, t) & = 0
\end{align}[/dtex]primijenimo metodu separacije varijabli. Nakon malo igranja, dobimo Sturm-Liouvilleovu zadaću [dtex]X'' + \lambda X = 0,\ X(0) = X(1) = 0.[/dtex] Njeno rješenje je [dtex]\lambda_k = (k \pi)^2,\ X_k(x) = \sin(k \pi x),\ k \in \mathbb{N}.[/dtex] Sad tražimo rješenje oblika [dtex]\sum_{k = 1}^{\infty}{T_k(t) X_k(x)}[/dtex] za [tex]v[/tex]. Kad to uvrtimo u PDJ za [tex]v[/tex], dobimo (nakon deriviranja i prebacivanja) [dtex]\sum_{k = 1}^{\infty}\left(T''_k(t) + (k \pi)^2 T_k(t)\right)\sin(k \pi x) = t^2 \sin(\pi x).[/dtex] Primijetio da je s desne strane Fourierov red (koje li slučajnosti). Zato smijemo izjednačiti izraze uz [tex]\sin(k \pi x)[/tex] s obje strane. Tako dobimo ODJ [dtex]\begin{align}
T''_1(t) + \pi^2 T_1(t) & = t^2 \\
T''_k(t) + (k \pi)^2 T_k(t) & = 0 \ \textrm{ za } k \geq 2
\end{align}[/dtex]
Nastavit ću ako netko pita. Konačno rješenje je [dtex]u(x, t) = \frac{(\pi^4 + 2) \cos(\pi t) + \pi^2 t^2 - 2}{\pi^4} \sin(\pi x) + \frac{\sin(2 \pi t)}{2 \pi} \sin(2 \pi x) + x + 1.[/dtex][/quote]
Bi htio please raspisat ovu prvu di je to sve jedanko t^2...ja to nikako ne uspijem :/
| pmli (napisa): | Ponovo 3.
Nakon supstitucije, dobimo početno-rubnu zadaću:
[dtex]\begin{align}
v_{tt} & = v_{xx} + t^2 \sin(\pi x) \ \textrm{ u } \ \langle 0, 1 \rangle \times \mathbb{R}^+ \\
v(x, 0) & = \sin(\pi x) \\
v_t(x, 0) & = \sin(2 \pi x) \\
v(0, t) & = 0 \\
v(1, t) & = 0
\end{align}[/dtex]
Na homogenu zadaću [dtex]\begin{align}
v_{tt}^H & = v_{xx}^H \ \textrm{ u } \ \langle 0, 1 \rangle \times \mathbb{R}^+ \\
v^H(x, 0) & = \sin(\pi x) \\
v_t^H(x, 0) & = \sin(2 \pi x) \\
v^H(0, t) & = 0 \\
v^H(1, t) & = 0
\end{align}[/dtex]primijenimo metodu separacije varijabli. Nakon malo igranja, dobimo Sturm-Liouvilleovu zadaću [dtex]X'' + \lambda X = 0,\ X(0) = X(1) = 0.[/dtex] Njeno rješenje je [dtex]\lambda_k = (k \pi)^2,\ X_k(x) = \sin(k \pi x),\ k \in \mathbb{N}.[/dtex] Sad tražimo rješenje oblika [dtex]\sum_{k = 1}^{\infty}{T_k(t) X_k(x)}[/dtex] za [tex]v[/tex]. Kad to uvrtimo u PDJ za [tex]v[/tex], dobimo (nakon deriviranja i prebacivanja) [dtex]\sum_{k = 1}^{\infty}\left(T''_k(t) + (k \pi)^2 T_k(t)\right)\sin(k \pi x) = t^2 \sin(\pi x).[/dtex] Primijetio da je s desne strane Fourierov red (koje li slučajnosti). Zato smijemo izjednačiti izraze uz [tex]\sin(k \pi x)[/tex] s obje strane. Tako dobimo ODJ [dtex]\begin{align}
T''_1(t) + \pi^2 T_1(t) & = t^2 \\
T''_k(t) + (k \pi)^2 T_k(t) & = 0 \ \textrm{ za } k \geq 2
\end{align}[/dtex]
Nastavit ću ako netko pita. Konačno rješenje je [dtex]u(x, t) = \frac{(\pi^4 + 2) \cos(\pi t) + \pi^2 t^2 - 2}{\pi^4} \sin(\pi x) + \frac{\sin(2 \pi t)}{2 \pi} \sin(2 \pi x) + x + 1.[/dtex] |
Bi htio please raspisat ovu prvu di je to sve jedanko t^2...ja to nikako ne uspijem 
|
|
| [Vrh] |
|
pmli
Forumaš(ica)

Pridružen/a: 09. 11. 2009. (12:03:05)
Postovi: (2C8)16
Spol: 
|
|
| [Vrh] |
|
Megy Poe
Forumaš(ica)

Pridružen/a: 05. 11. 2009. (23:14:52)
Postovi: (122)16
|
 Postano: 12:27 ned, 10. 6. 2012 Naslov: Postano: 12:27 ned, 10. 6. 2012 Naslov: |
    |
|
|
[quote="pmli"][tex]T''_1(t) + \pi^2 T_1(t) = t^2[/tex] je linearna, nehomogena ODJ. Rješenje homogenog dijela je [tex]A \cos(\pi t) + B \sin(\pi t)[/tex], a tražimo partikularno rješenje u obliku polinoma 2. stupnja, tj. [tex]C t^2 + D t + E[/tex], jer je nehomogeni dio baš polinom 2. stupnja (i nema ga u rješenju homogenog dijela).[/quote]
Ja sam to isto zakljucila al ne razumijem kak dobiješ ove pijeve? Ja kad to uvrstim dobijem da mi je C=1, A=1 a ostalo 0 :/
| pmli (napisa): | | [tex]T''_1(t) + \pi^2 T_1(t) = t^2[/tex] je linearna, nehomogena ODJ. Rješenje homogenog dijela je [tex]A \cos(\pi t) + B \sin(\pi t)[/tex], a tražimo partikularno rješenje u obliku polinoma 2. stupnja, tj. [tex]C t^2 + D t + E[/tex], jer je nehomogeni dio baš polinom 2. stupnja (i nema ga u rješenju homogenog dijela). |
Ja sam to isto zakljucila al ne razumijem kak dobiješ ove pijeve? Ja kad to uvrstim dobijem da mi je C=1, A=1 a ostalo 0 
|
|
| [Vrh] |
|
KG
Forumaš(ica)
Pridružen/a: 26. 01. 2011. (15:50:24)
Postovi: (30)16
Spol: 
|
|
| [Vrh] |
|
pmli
Forumaš(ica)

Pridružen/a: 09. 11. 2009. (12:03:05)
Postovi: (2C8)16
Spol: 
|
 Postano: 12:47 ned, 10. 6. 2012 Naslov: Postano: 12:47 ned, 10. 6. 2012 Naslov: |
    |
|
|
[quote="Megy Poe"][quote="pmli"][tex]T''_1(t) + \pi^2 T_1(t) = t^2[/tex] je linearna, nehomogena ODJ. Rješenje homogenog dijela je [tex]A \cos(\pi t) + B \sin(\pi t)[/tex], a tražimo partikularno rješenje u obliku polinoma 2. stupnja, tj. [tex]C t^2 + D t + E[/tex], jer je nehomogeni dio baš polinom 2. stupnja (i nema ga u rješenju homogenog dijela).[/quote]
Ja sam to isto zakljucila al ne razumijem kak dobiješ ove pijeve? Ja kad to uvrstim dobijem da mi je C=1, A=1 a ostalo 0 :/[/quote]
Prvo uvrstiš partikularno rješenje u ODJ da odrediš [tex]C[/tex], [tex]D[/tex] i [tex]E[/tex]: [dtex]\begin{align}
(C t^2 + D t + E)'' + \pi^2 (C t^2 + D t + E) & = t^2 \\
2 C + \pi^2 C t^2 + \pi^2 D t + \pi^2 E & = t^2
\end{align}[/dtex] Znači, dobiš sustav [dtex]\begin{align}
\pi^2 C & = 1 \\
\pi^2 D & = 0 \\
2 C + \pi^2 E & = 0
\end{align}[/dtex] Koeficijente [tex]A[/tex] i [tex]B[/tex] odrediš iz početnog uvjeta (iz početnog uvjeta za [tex]v[/tex] dobiš početni uvjet za [tex]T_k[/tex]).
[quote="KG"]Jel mi može netko malo pomoć oko ovog 4. zad: http://web.math.pmf.unizg.hr/nastava/mmf/kolokviji/mmf2kol2012.pdf
Raspišem na 3 slučaja ovisno o x i y i problem je u eliptičkom slučaju kad bi trebao dobit A=C. Ja dobijem da je A=-C i to bi trebalo značit da imam negdje nekakvu grešku, al nikak da otkrijem gdje???[/quote]
Pa, ne mogu ti baš pomoći, zar ne? Najviše što ti mogu reći je da paziš da ti je uvijek pozitivan broj pod korijenom, na predznake i deriviraš li ok.
I da, ne moraš raspisivati parabolički slučaj, jer se on događa na osima. Također, kad bi se radilo kak spada, trebalo bi raspisivati za svaki kvadrant posebno zbog raznih mogućih predznaka.
| Megy Poe (napisa): | | pmli (napisa): | | [tex]T''_1(t) + \pi^2 T_1(t) = t^2[/tex] je linearna, nehomogena ODJ. Rješenje homogenog dijela je [tex]A \cos(\pi t) + B \sin(\pi t)[/tex], a tražimo partikularno rješenje u obliku polinoma 2. stupnja, tj. [tex]C t^2 + D t + E[/tex], jer je nehomogeni dio baš polinom 2. stupnja (i nema ga u rješenju homogenog dijela). |
Ja sam to isto zakljucila al ne razumijem kak dobiješ ove pijeve? Ja kad to uvrstim dobijem da mi je C=1, A=1 a ostalo 0  |
Prvo uvrstiš partikularno rješenje u ODJ da odrediš [tex]C[/tex], [tex]D[/tex] i [tex]E[/tex]: [dtex]\begin{align}
(C t^2 + D t + E)'' + \pi^2 (C t^2 + D t + E) & = t^2 \\
2 C + \pi^2 C t^2 + \pi^2 D t + \pi^2 E & = t^2
\end{align}[/dtex] Znači, dobiš sustav [dtex]\begin{align}
\pi^2 C & = 1 \\
\pi^2 D & = 0 \\
2 C + \pi^2 E & = 0
\end{align}[/dtex] Koeficijente [tex]A[/tex] i [tex]B[/tex] odrediš iz početnog uvjeta (iz početnog uvjeta za [tex]v[/tex] dobiš početni uvjet za [tex]T_k[/tex]).
Pa, ne mogu ti baš pomoći, zar ne? Najviše što ti mogu reći je da paziš da ti je uvijek pozitivan broj pod korijenom, na predznake i deriviraš li ok.
I da, ne moraš raspisivati parabolički slučaj, jer se on događa na osima. Također, kad bi se radilo kak spada, trebalo bi raspisivati za svaki kvadrant posebno zbog raznih mogućih predznaka.
|
|
| [Vrh] |
|
Megy Poe
Forumaš(ica)

Pridružen/a: 05. 11. 2009. (23:14:52)
Postovi: (122)16
|
 Postano: 13:16 ned, 10. 6. 2012 Naslov: Postano: 13:16 ned, 10. 6. 2012 Naslov: |
    |
|
|
[quote="pmli"][quote="Megy Poe"][quote="pmli"][tex]T''_1(t) + \pi^2 T_1(t) = t^2[/tex] je linearna, nehomogena ODJ. Rješenje homogenog dijela je [tex]A \cos(\pi t) + B \sin(\pi t)[/tex], a tražimo partikularno rješenje u obliku polinoma 2. stupnja, tj. [tex]C t^2 + D t + E[/tex], jer je nehomogeni dio baš polinom 2. stupnja (i nema ga u rješenju homogenog dijela).[/quote]
Ja sam to isto zakljucila al ne razumijem kak dobiješ ove pijeve? Ja kad to uvrstim dobijem da mi je C=1, A=1 a ostalo 0 :/[/quote]
Prvo uvrstiš partikularno rješenje u ODJ da odrediš [tex]C[/tex], [tex]D[/tex] i [tex]E[/tex]: [dtex]\begin{align}
(C t^2 + D t + E)'' + \pi^2 (C t^2 + D t + E) & = t^2 \\
2 C + \pi^2 C t^2 + \pi^2 D t + \pi^2 E & = t^2
\end{align}[/dtex] Znači, dobiš sustav [dtex]\begin{align}
\pi^2 C & = 1 \\
\pi^2 D & = 0 \\
2 C + \pi^2 E & = 0
\end{align}[/dtex] Koeficijente [tex]A[/tex] i [tex]B[/tex] odrediš iz početnog uvjeta (iz početnog uvjeta za [tex]v[/tex] dobiš početni uvjet za [tex]T_k[/tex]).
[quote="KG"]Jel mi može netko malo pomoć oko ovog 4. zad: http://web.math.pmf.unizg.hr/nastava/mmf/kolokviji/mmf2kol2012.pdf
Raspišem na 3 slučaja ovisno o x i y i problem je u eliptičkom slučaju kad bi trebao dobit A=C. Ja dobijem da je A=-C i to bi trebalo značit da imam negdje nekakvu grešku, al nikak da otkrijem gdje???[/quote]
Pa, ne mogu ti baš pomoći, zar ne? Najviše što ti mogu reći je da paziš da ti je uvijek pozitivan broj pod korijenom, na predznake i deriviraš li ok.
I da, ne moraš raspisivati parabolički slučaj, jer se on događa na osima. Također, kad bi se radilo kak spada, trebalo bi raspisivati za svaki kvadrant posebno zbog raznih mogućih predznaka.[/quote]
Hvala puno
| pmli (napisa): | | Megy Poe (napisa): | | pmli (napisa): | | [tex]T''_1(t) + \pi^2 T_1(t) = t^2[/tex] je linearna, nehomogena ODJ. Rješenje homogenog dijela je [tex]A \cos(\pi t) + B \sin(\pi t)[/tex], a tražimo partikularno rješenje u obliku polinoma 2. stupnja, tj. [tex]C t^2 + D t + E[/tex], jer je nehomogeni dio baš polinom 2. stupnja (i nema ga u rješenju homogenog dijela). |
Ja sam to isto zakljucila al ne razumijem kak dobiješ ove pijeve? Ja kad to uvrstim dobijem da mi je C=1, A=1 a ostalo 0  |
Prvo uvrstiš partikularno rješenje u ODJ da odrediš [tex]C[/tex], [tex]D[/tex] i [tex]E[/tex]: [dtex]\begin{align}
(C t^2 + D t + E)'' + \pi^2 (C t^2 + D t + E) & = t^2 \\
2 C + \pi^2 C t^2 + \pi^2 D t + \pi^2 E & = t^2
\end{align}[/dtex] Znači, dobiš sustav [dtex]\begin{align}
\pi^2 C & = 1 \\
\pi^2 D & = 0 \\
2 C + \pi^2 E & = 0
\end{align}[/dtex] Koeficijente [tex]A[/tex] i [tex]B[/tex] odrediš iz početnog uvjeta (iz početnog uvjeta za [tex]v[/tex] dobiš početni uvjet za [tex]T_k[/tex]).
Pa, ne mogu ti baš pomoći, zar ne? Najviše što ti mogu reći je da paziš da ti je uvijek pozitivan broj pod korijenom, na predznake i deriviraš li ok.
I da, ne moraš raspisivati parabolički slučaj, jer se on događa na osima. Također, kad bi se radilo kak spada, trebalo bi raspisivati za svaki kvadrant posebno zbog raznih mogućih predznaka. |
Hvala puno
|
|
| [Vrh] |
|
|












