| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
kiara
Forumaš(ica)
Pridružen/a: 15. 11. 2011. (23:22:57)
Postovi: (55)16
|
|
| [Vrh] |
|
satja
Forumaš(ica)
Pridružen/a: 16. 05. 2010. (10:44:17)
Postovi: (F1)16
|
|
| [Vrh] |
|
kiara
Forumaš(ica)
Pridružen/a: 15. 11. 2011. (23:22:57)
Postovi: (55)16
|
 Postano: 20:01 čet, 7. 6. 2012 Naslov: |
    |
|
|
[quote="satja"]Bit će nam lakše odgovoriti ako kažeš koji točno korak ne razumiješ :)[/quote]
:)
Kad uzmemo δ=min{c, 1-c}, i onda razumijem da ima barem jedan zajednicki rub sa intervalom [0, 1]. I sada dalje do kontradikcije ne razumijem. Tocnije, ovo iz skripte: "Buduci da je g(c−δ) = 0 ili g(c+δ) = 0, to je desna strana od (4.31) strogo manja od g(c), sto je kontradikcija s cinjenicom da je g(c) > 0 maksimum."
| satja (napisa): | Bit će nam lakše odgovoriti ako kažeš koji točno korak ne razumiješ  |
Kad uzmemo δ=min{c, 1-c}, i onda razumijem da ima barem jedan zajednicki rub sa intervalom [0, 1]. I sada dalje do kontradikcije ne razumijem. Tocnije, ovo iz skripte: "Buduci da je g(c−δ) = 0 ili g(c+δ) = 0, to je desna strana od (4.31) strogo manja od g(c), sto je kontradikcija s cinjenicom da je g(c) > 0 maksimum."
|
|
| [Vrh] |
|
Zenon
Forumaš(ica)
Pridružen/a: 09. 09. 2011. (19:14:43)
Postovi: (2B1)16
Sarma: -
Lokacija: [tex]\pm\infty[/tex]
|
|
| [Vrh] |
|
kiara
Forumaš(ica)
Pridružen/a: 15. 11. 2011. (23:22:57)
Postovi: (55)16
|
|
| [Vrh] |
|
dalmatinčica
Forumaš(ica)
Pridružen/a: 01. 10. 2011. (18:46:54)
Postovi: (AC)16
|
|
| [Vrh] |
|
quark
Forumaš(ica)
Pridružen/a: 22. 10. 2011. (16:47:39)
Postovi: (DA)16
Spol: 
|
|
| [Vrh] |
|
dalmatinčica
Forumaš(ica)
Pridružen/a: 01. 10. 2011. (18:46:54)
Postovi: (AC)16
|
|
| [Vrh] |
|
quark
Forumaš(ica)
Pridružen/a: 22. 10. 2011. (16:47:39)
Postovi: (DA)16
Spol:
|
| Postano: 22:54 pet, 8. 6. 2012 Naslov: |
|
|
|
Opet pdf, ali dobro :D
Ipak ti se samo čini; možda te zbunjuje što je integral od 2, ali to uopće ne utječe na konvergenciju, samo na sumu (koja nas ne zanima). Integralni uvjet traži padajuću funkciju, dakle, mogli smo izabrati i bilokoji broj veći od 2.
Opet pdf, ali dobro 
Ipak ti se samo čini; možda te zbunjuje što je integral od 2, ali to uopće ne utječe na konvergenciju, samo na sumu (koja nas ne zanima). Integralni uvjet traži padajuću funkciju, dakle, mogli smo izabrati i bilokoji broj veći od 2.
|
|
| [Vrh] |
|
dalmatinčica
Forumaš(ica)
Pridružen/a: 01. 10. 2011. (18:46:54)
Postovi: (AC)16
|
|
| [Vrh] |
|
Lux86
Forumaš(ica)
Pridružen/a: 11. 09. 2011. (23:38:43)
Postovi: (1D)16
Spol: 
|
|
| [Vrh] |
|
goranm
Forumaš(ica)
Pridružen/a: 12. 11. 2002. (20:09:12)
Postovi: (906)16
Spol:
|
|
| [Vrh] |
|
Lux86
Forumaš(ica)
Pridružen/a: 11. 09. 2011. (23:38:43)
Postovi: (1D)16
Spol:
|
| Postano: 18:41 sub, 9. 6. 2012 Naslov: |
|
|
|
[quote="goranm"][quote="Lux86"]kako dokazati da je lim(1+1/x)^x, kad x->+besk jednako e?
samo na temelju definicije e=lim(1+1/n)^n[/quote]
Najprije dokazuješ da je niz [latex]\displaystyle\lim_{x\to\infty}(1+1/x)^x[/latex] strogo rastuć i omeđen odozgo (što povlači da je i konvergentan), a točku prema kojoj taj niz konvergira nazoveš e.
Za detalje vidi ovdje:
http://degiorgi.math.hr/forum/viewtopic.php?t=6269&postdays=0&postorder=asc&&start=23[/quote]
hvala :)
mene zapravo najviše muči prelazak s prirodnih na realne brojeve. u prvom semestru smo izveli taj dokaz za niz (1+1/n)^n, pri čemu su n prirodni, i sad je profesor rekao da se lako pokaže da i za realne x ovo vrijedi. znači li to da zapravo ponavljamo isti postupak ili?
ispričavam se ako je glupo pitanje :oops:
jel bi možda bilo dovoljno pokazati da je niz (1+1/x)^x rastuć i omeđen odozgo, pa je konvergentan i onda reći da budući da je (1+1/n)^n njegov podniz koji konvergira u e, limes i tog niza e?
hvala
mene zapravo najviše muči prelazak s prirodnih na realne brojeve. u prvom semestru smo izveli taj dokaz za niz (1+1/n)^n, pri čemu su n prirodni, i sad je profesor rekao da se lako pokaže da i za realne x ovo vrijedi. znači li to da zapravo ponavljamo isti postupak ili?
ispričavam se ako je glupo pitanje 
jel bi možda bilo dovoljno pokazati da je niz (1+1/x)^x rastuć i omeđen odozgo, pa je konvergentan i onda reći da budući da je (1+1/n)^n njegov podniz koji konvergira u e, limes i tog niza e?
|
|
| [Vrh] |
|
goranm
Forumaš(ica)
Pridružen/a: 12. 11. 2002. (20:09:12)
Postovi: (906)16
Spol:
|
| Postano: 20:22 sub, 9. 6. 2012 Naslov: |
|
|
|
[quote="Lux86"]ispričavam se ako je glupo pitanje :oops:[/quote]
Sasvim je pametno pitanje i jako lijepo ilustrira moju nepažnju u čitanju postova. :)
[quote]jel bi možda bilo dovoljno pokazati da je niz (1+1/x)^x rastuć i omeđen odozgo, pa je konvergentan i onda reći da budući da je (1+1/n)^n njegov podniz koji konvergira u e, limes i tog niza e?[/quote]
To bi bilo dovoljno, ali ne smiješ koristiti induktivni argument iz dokaza u slučaju prirodnih brojeva jer [url=http://en.wikipedia.org/wiki/Binomial_series]binomni teorem s realnim eksponentom[/url] nešto drugačije izgleda.
Pretpostavljam da se cilja na dokaz preko definicije limesa funkcije.
[spoiler]
Neka je [latex]f\colon \left[1,\infty\right\rangle\to\left\langle0,\infty\right\rangle[/latex] definirana s f(x)=(1+1/x)^x. (Nisam uzeo najveću moguću domenu jer nas zanima što se događa s x kad ide u beskonačno, ovi dijelovi ranije nam nisu zanimljivi).
Tvrdim da ta funkcija konvergira prema e kada x ide u beskonačnost: neka je [latex]\varepsilon >0[/latex]. Tražimo [latex]\delta>0[/latex] td. za svaki [latex]x\in\left[1,\infty\right\rangle[/latex] vrijedi [latex]x>\delta \Rightarrow |f(x)-e|<\varepsilon.[/latex]
Zbog konvergencije niza [latex](f(n))_{n\in\mathbb{N}}[/latex], kada n ide u beskonačno znamo da postoji prirodan N td. za svaki [latex]n\geq N[/latex] je [latex]|f(n)-e|<\varepsilon[/latex]. Uzmimo onda [latex]\delta=N[/latex].
Neka je [latex]x\in\left[1,\infty\right\rangle[/latex] td. je [latex]x>N[/latex]. Jer je funkcija f rastuća (lako se provjeri derivacijom), onda je f(N)<f(x). Kako je [latex]-\varepsilon+e<f(N)[/latex], onda je [latex]-\varepsilon+e<f(x)[/latex].
Očito postoji n>x pa je zbog [latex]f(n)<\varepsilon+e[/latex] onda i [latex]f(x)<f(n)<\varepsilon+e[/latex], tj. [latex]-\varepsilon+e<f(x)<\varepsilon+e[/latex], odnosno [latex]|f(x)-e|<\varepsilon.[/latex]
[/spoiler]
| Lux86 (napisa): | | ispričavam se ako je glupo pitanje |
Sasvim je pametno pitanje i jako lijepo ilustrira moju nepažnju u čitanju postova.
| Citat: | | jel bi možda bilo dovoljno pokazati da je niz (1+1/x)^x rastuć i omeđen odozgo, pa je konvergentan i onda reći da budući da je (1+1/n)^n njegov podniz koji konvergira u e, limes i tog niza e? |
To bi bilo dovoljno, ali ne smiješ koristiti induktivni argument iz dokaza u slučaju prirodnih brojeva jer binomni teorem s realnim eksponentom nešto drugačije izgleda.
Pretpostavljam da se cilja na dokaz preko definicije limesa funkcije.
| Spoiler [hidden; click to show]: |
Neka je 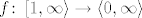 definirana s f(x)=(1+1/x)^x. (Nisam uzeo najveću moguću domenu jer nas zanima što se događa s x kad ide u beskonačno, ovi dijelovi ranije nam nisu zanimljivi).
Tvrdim da ta funkcija konvergira prema e kada x ide u beskonačnost: neka je 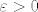 . Tražimo 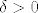 td. za svaki 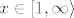 vrijedi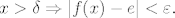 
Zbog konvergencije niza 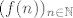 , kada n ide u beskonačno znamo da postoji prirodan N td. za svaki  je 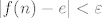 . Uzmimo onda  .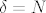
Neka je 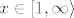td. je 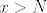 . Jer je funkcija f rastuća (lako se provjeri derivacijom), onda je f(N)<f(x). Kako je 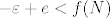 , onda je  .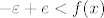
Očito postoji n>x pa je zbog 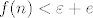 onda i 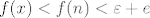 , tj. 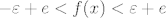 , odnosno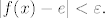 
|
_________________
The Dude Abides
|
|
| [Vrh] |
|
Lux86
Forumaš(ica)
Pridružen/a: 11. 09. 2011. (23:38:43)
Postovi: (1D)16
Spol:
|
|
| [Vrh] |
|
quark
Forumaš(ica)
Pridružen/a: 22. 10. 2011. (16:47:39)
Postovi: (DA)16
Spol:
|
|
| [Vrh] |
|
Zenon
Forumaš(ica)
Pridružen/a: 09. 09. 2011. (19:14:43)
Postovi: (2B1)16
Sarma: -
Lokacija: [tex]\pm\infty[/tex]
|
| Postano: 22:38 pon, 11. 6. 2012 Naslov: |
|
|
|
[quote="goranm"]Jer je funkcija f rastuća (lako se provjeri derivacijom), [/quote]
Ovaj naivan pristup sam imao i ja :P
Krivo. Kada bismo dokazivali da je f rastuća preko derivacija, morali bismo dokazati da je funkcija diferencijabilna. Za diferencijabilnost te funkcije nam svakako treba diferencijabilnost od [tex]e^x[/tex] i [tex]\ln x[/tex], a njihova diferencijabilnost se i dokazuje pomoću činjenice da je [tex]\displaystyle e=\underset{x\in\mathbb R}{\underset{x\to +\infty}{\text{lim}}}\left(1+\frac 1x\right)^x[/tex]. Barem smo mi to tako radili na predavanjima. U svakom slučaju, ukoliko se na neki drugi način ne dokaže diferencijabilnost funkcije f (tj. bez korištenja činjenice da su [tex]e^x[/tex] i [tex]\ln x[/tex] diferencijabilne), to nije valjan dokaz.
| goranm (napisa): | | Jer je funkcija f rastuća (lako se provjeri derivacijom), |
Ovaj naivan pristup sam imao i ja 
Krivo. Kada bismo dokazivali da je f rastuća preko derivacija, morali bismo dokazati da je funkcija diferencijabilna. Za diferencijabilnost te funkcije nam svakako treba diferencijabilnost od [tex]e^x[/tex] i [tex]\ln x[/tex], a njihova diferencijabilnost se i dokazuje pomoću činjenice da je [tex]\displaystyle e=\underset{x\in\mathbb R}{\underset{x\to +\infty}{\text{lim}}}\left(1+\frac 1x\right)^x[/tex]. Barem smo mi to tako radili na predavanjima. U svakom slučaju, ukoliko se na neki drugi način ne dokaže diferencijabilnost funkcije f (tj. bez korištenja činjenice da su [tex]e^x[/tex] i [tex]\ln x[/tex] diferencijabilne), to nije valjan dokaz.
|
|
| [Vrh] |
|
Loo
Forumaš(ica)
Pridružen/a: 11. 06. 2012. (16:02:07)
Postovi: (D0)16
Spol: 
|
| Postano: 23:36 pon, 11. 6. 2012 Naslov: |
|
|
|
[quote="Zenon"][quote="goranm"]Jer je funkcija f rastuća (lako se provjeri derivacijom), [/quote]
Ovaj naivan pristup sam imao i ja :P
Krivo. Kada bismo dokazivali da je f rastuća preko derivacija, morali bismo dokazati da je funkcija diferencijabilna. Za diferencijabilnost te funkcije nam svakako treba diferencijabilnost od [tex]e^x[/tex] i [tex]\ln x[/tex], a njihova diferencijabilnost se i dokazuje pomoću činjenice da je [tex]\displaystyle e=\underset{x\in\mathbb R}{\underset{x\to +\infty}{\text{lim}}}\left(1+\frac 1x\right)^x[/tex]. Barem smo mi to tako radili na predavanjima. U svakom slučaju, ukoliko se na neki drugi način ne dokaže diferencijabilnost funkcije f (tj. bez korištenja činjenice da su [tex]e^x[/tex] i [tex]\ln x[/tex] diferencijabilne), to nije valjan dokaz.[/quote]
a da pokažeš kako onda? :wink:
| Zenon (napisa): | | goranm (napisa): | | Jer je funkcija f rastuća (lako se provjeri derivacijom), |
Ovaj naivan pristup sam imao i ja
Krivo. Kada bismo dokazivali da je f rastuća preko derivacija, morali bismo dokazati da je funkcija diferencijabilna. Za diferencijabilnost te funkcije nam svakako treba diferencijabilnost od [tex]e^x[/tex] i [tex]\ln x[/tex], a njihova diferencijabilnost se i dokazuje pomoću činjenice da je [tex]\displaystyle e=\underset{x\in\mathbb R}{\underset{x\to +\infty}{\text{lim}}}\left(1+\frac 1x\right)^x[/tex]. Barem smo mi to tako radili na predavanjima. U svakom slučaju, ukoliko se na neki drugi način ne dokaže diferencijabilnost funkcije f (tj. bez korištenja činjenice da su [tex]e^x[/tex] i [tex]\ln x[/tex] diferencijabilne), to nije valjan dokaz. |
a da pokažeš kako onda? 
|
|
| [Vrh] |
|
malalodacha
Forumaš(ica)
Pridružen/a: 11. 10. 2011. (17:06:13)
Postovi: (79)16
|
|
| [Vrh] |
|
goranm
Forumaš(ica)
Pridružen/a: 12. 11. 2002. (20:09:12)
Postovi: (906)16
Spol:
|
| Postano: 2:28 uto, 12. 6. 2012 Naslov: |
|
|
|
[quote="Zenon"]Ovaj naivan pristup sam imao i ja :P
Krivo. Kada bismo dokazivali da je f rastuća preko derivacija, morali bismo dokazati da je funkcija diferencijabilna. Za diferencijabilnost te funkcije nam svakako treba diferencijabilnost od [tex]e^x[/tex] i [tex]\ln x[/tex], a njihova diferencijabilnost se i dokazuje pomoću činjenice da je [tex]\displaystyle e=\underset{x\in\mathbb R}{\underset{x\to +\infty}{\text{lim}}}\left(1+\frac 1x\right)^x[/tex]. Barem smo mi to tako radili na predavanjima.[/quote]
Za pokazati derivabilnost od e^x dovoljno je znati da je funkcija e^x po definiciji jednaka limesu [u]niza[/u] (1+x/n)^n, za nenegativne x-eve. Nije potrebno definirati e onako kako si naveo, tako da sve štima s mojim dokazom. Ako je što krivo, onda su to tvoje bilješke s predavanja. :P
Kako ste pokazali da [tex]\displaystyle\underset{x\in\mathbb R}{\underset{x\to +\infty}{\text{lim}}}\left(1+\frac 1x\right)^x[/tex] konvergira (što ste morali pokazati ako ste nalijepili da je to jednako e)?
[quote="Zenon"]U svakom slučaju, ukoliko se na neki drugi način ne dokaže diferencijabilnost funkcije f (tj. bez korištenja činjenice da su [tex]e^x[/tex] i [tex]\ln x[/tex] diferencijabilne), to nije valjan dokaz.[/quote]
Krivo. :P Dokaz je valjan bez obzira na derivabilnost funkcije f, dovoljno je pokazat njenu strogu monotonost. Može biti da tehnika kojom će se to pokazati nije valjana (iako je!).
| Zenon (napisa): | Ovaj naivan pristup sam imao i ja
Krivo. Kada bismo dokazivali da je f rastuća preko derivacija, morali bismo dokazati da je funkcija diferencijabilna. Za diferencijabilnost te funkcije nam svakako treba diferencijabilnost od [tex]e^x[/tex] i [tex]\ln x[/tex], a njihova diferencijabilnost se i dokazuje pomoću činjenice da je [tex]\displaystyle e=\underset{x\in\mathbb R}{\underset{x\to +\infty}{\text{lim}}}\left(1+\frac 1x\right)^x[/tex]. Barem smo mi to tako radili na predavanjima. |
Za pokazati derivabilnost od e^x dovoljno je znati da je funkcija e^x po definiciji jednaka limesu niza (1+x/n)^n, za nenegativne x-eve. Nije potrebno definirati e onako kako si naveo, tako da sve štima s mojim dokazom. Ako je što krivo, onda su to tvoje bilješke s predavanja.
Kako ste pokazali da [tex]\displaystyle\underset{x\in\mathbb R}{\underset{x\to +\infty}{\text{lim}}}\left(1+\frac 1x\right)^x[/tex] konvergira (što ste morali pokazati ako ste nalijepili da je to jednako e)?
| Zenon (napisa): | | U svakom slučaju, ukoliko se na neki drugi način ne dokaže diferencijabilnost funkcije f (tj. bez korištenja činjenice da su [tex]e^x[/tex] i [tex]\ln x[/tex] diferencijabilne), to nije valjan dokaz. |
Krivo. Dokaz je valjan bez obzira na derivabilnost funkcije f, dovoljno je pokazat njenu strogu monotonost. Može biti da tehnika kojom će se to pokazati nije valjana (iako je!).
_________________
The Dude Abides
|
|
| [Vrh] |
|
|
Hvala!
