| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
Gost
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
suza
Forumaš(ica)

Pridružen/a: 24. 10. 2009. (14:37:50)
Postovi: (65)16
Spol: 
|
|
| [Vrh] |
|
Gost
|
 Postano: 13:30 čet, 31. 5. 2012 Naslov: Postano: 13:30 čet, 31. 5. 2012 Naslov: |
    |
|
|
[quote="Anonymous"]Da li bi netko znao detaljno (po (definicijama) raspisati konvergencije [latex]\lambda-ss[/latex] (tj. po točkama) i po mjeri ovih fja
[latex]f_n=n^21_{<1-\frac{1}n,1>}[/latex]
[latex]f_n=n^\frac{1}3 1_{<\frac{1}n,\frac{n}2>}[/latex]
Po intervalima za x, te po mjeri (formalan zapis).
Hvala od srca onome tko pomogne! :)[/quote]
Gledam ovu drugu i buduci da se širi po cijelom [0, +besk.> a
[latex]f_n=n^\frac{1}3[/latex] ne konvergira nemamo po točki, pa nemamo ni uniformnu, pa nemamo ni kandidata.
Kako dokazati za ostale konvergencije kad nemamo "kandidata", jer su se svi zadaci iz vježbi pozivali na to da smo našli f, pa za proizvoljnu fju g mora ici f = g lambda s.s. itd...
| Anonymous (napisa): | Da li bi netko znao detaljno (po (definicijama) raspisati konvergencije 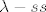 (tj. po točkama) i po mjeri ovih fja (tj. po točkama) i po mjeri ovih fja
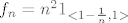
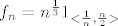
Po intervalima za x, te po mjeri (formalan zapis).
Hvala od srca onome tko pomogne!  |
Gledam ovu drugu i buduci da se širi po cijelom [0, +besk.> a
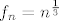 ne konvergira nemamo po točki, pa nemamo ni uniformnu, pa nemamo ni kandidata. ne konvergira nemamo po točki, pa nemamo ni uniformnu, pa nemamo ni kandidata.
Kako dokazati za ostale konvergencije kad nemamo "kandidata", jer su se svi zadaci iz vježbi pozivali na to da smo našli f, pa za proizvoljnu fju g mora ici f = g lambda s.s. itd...
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
komaPMF
Forumaš(ica)


Pridružen/a: 22. 11. 2007. (10:23:41)
Postovi: (E6)16
Spol: 
Lokacija: Over the roof
|
 Postano: 18:51 čet, 31. 5. 2012 Naslov: Postano: 18:51 čet, 31. 5. 2012 Naslov: |
    |
|
|
Ja sam 13. ovako:
[latex]f\in L^p[/latex] ako [latex]{||f||_p } <\infty[/latex] tj kad to dignemo na p-tu, tražimo za koji p nam je [latex]\int \frac{|cos(n\pi)|^p}{n^{p/3}} d\mu[/latex] konačan.
A kako imamo da je [tex]\mu[/tex] brojeća mjera, i [tex]|f(n)|[/tex] pozitivna funkcija, tako je integral jednak sumi po n ide od 1 do besk. Sada primijetimo da je [tex]|cos(n\pi)|[/tex] jednak 1 za svaki n prirodan broj. Dakle, tražimo za koje p-ove će nam red [latex] \sum_{n=1}^{\infty} (\frac{1}{n})^{\frac{p}{3}}[/latex] konvergirati.
Ovdje u skripti http://web.math.pmf.unizg.hr/~guljas/skripte/MATANALuR.pdf, str. 164., piše da red (1/n)^p kvgira za p>=2 pa tražimo kad nam vrijedi [tex]\frac{p}{3}\ge 2[/tex] i to bi trebalo biti rješenje. Molim nekog da provjeri jer nisam ni ja sigurna u ovo...
Ja sam 13. ovako:
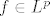 ako ako 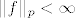 tj kad to dignemo na p-tu, tražimo za koji p nam je tj kad to dignemo na p-tu, tražimo za koji p nam je 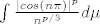 konačan. konačan.
A kako imamo da je [tex]\mu[/tex] brojeća mjera, i [tex]|f(n)|[/tex] pozitivna funkcija, tako je integral jednak sumi po n ide od 1 do besk. Sada primijetimo da je [tex]|cos(n\pi)|[/tex] jednak 1 za svaki n prirodan broj. Dakle, tražimo za koje p-ove će nam red 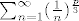 konvergirati. konvergirati.
Ovdje u skripti http://web.math.pmf.unizg.hr/~guljas/skripte/MATANALuR.pdf, str. 164., piše da red (1/n)^p kvgira za p>=2 pa tražimo kad nam vrijedi [tex]\frac{p}{3}\ge 2[/tex] i to bi trebalo biti rješenje. Molim nekog da provjeri jer nisam ni ja sigurna u ovo...
_________________
Granice mogućega možemo odrediti samo onda ako ih prijeđemo odlaskom u nemoguće
Zadnja promjena: komaPMF; 21:04 čet, 31. 5. 2012; ukupno mijenjano 1 put.
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
komaPMF
Forumaš(ica)


Pridružen/a: 22. 11. 2007. (10:23:41)
Postovi: (E6)16
Spol: 
Lokacija: Over the roof
|
|
| [Vrh] |
|
komaPMF
Forumaš(ica)


Pridružen/a: 22. 11. 2007. (10:23:41)
Postovi: (E6)16
Spol: 
Lokacija: Over the roof
|
|
| [Vrh] |
|
vjekovac
Forumaš(ica)


Pridružen/a: 23. 01. 2003. (18:26:55)
Postovi: (2DB)16
Spol: 
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
sunny
Forumaš(ica)

Pridružen/a: 21. 01. 2007. (01:06:34)
Postovi: (153)16
|
|
| [Vrh] |
|
lanek
Forumaš(ica)


Pridružen/a: 06. 10. 2009. (21:51:48)
Postovi: (51)16
Spol: 
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
irena0102
Forumaš(ica)


Pridružen/a: 01. 02. 2010. (11:49:52)
Postovi: (45)16
Spol: 
|
|
| [Vrh] |
|
lanek
Forumaš(ica)


Pridružen/a: 06. 10. 2009. (21:51:48)
Postovi: (51)16
Spol: 
|
|
| [Vrh] |
|
sunny
Forumaš(ica)

Pridružen/a: 21. 01. 2007. (01:06:34)
Postovi: (153)16
|
|
| [Vrh] |
|
|












