| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
Gost
|
|
| [Vrh] |
|
Jaca
Forumaš(ica)
Pridružen/a: 14. 10. 2005. (01:44:54)
Postovi: (E)16
|
 Postano: 20:27 uto, 11. 7. 2006 Naslov: Postano: 20:27 uto, 11. 7. 2006 Naslov: |
    |
|
|
Moja pitanja:
1. Što znate reći o centru grupe?
Kakva je to grupa? (normalna podgrupa)
Da li centar može biti jednak cijeloj grupi? (da, kada je grupa Abelova)
2. Koliko ima Abelovih grupa reda 72? (6, treba sve raspisati po teoremu o konačno generiranim Abelovim grupama)Koja od njih je izomorfna grupi Z72?
3.Kada je grupa prosta? ( kada nema pravih normalnih podgrupa)
4. Primjer faktorijalne domene koja nije domena glavnih ideala. ( Z[x] - treba o tome pričati, zašto to nije domena glavnih ideala, može biti generirana s dva elementa(?), pokazati to....)
5.Proširenje Q( 3^(1/2) )! Dimenzija ovog polja! Kako znamo kolika je? Minimalni polinom, kakav je (ireducibilan). Koja je baza?
Savjet: Učite primjere! Profesor traži razumijevanje teorema na primjerima. Ja sam se kod učenja više koncentrirala na to da dobro naučim sve iskaze, pa se nisam baš proslavila (iako sam prošla).
Dokaze ne trebate, ali primjere OBAVEZNO!!
-----------------------------------------------------------------------
Pitanja drugih ljudi ([i]zapisala [b]vifi[/b] [/i] :wave: ) :
1.Cauchieva lema (Tm XXXVI)
Prvi Silovljev tm
-zasto je lema bitna za 1 Silovljev tm
2.prost ideal,ireducibilan ideal, max i prost element
- ko koga povlaci i kada je ekvivalentno
3.Kako prosiriti polje Q( 2^(1/2) , 5^(1/3) ) ?
-objasniti kako to polje izgleda i kolika mu je duljina
---------
1.Tm o konacno generiranim Abelovim grupama
2.Razlika kod prstena, koja je struktura Z[x], Q[x] F[x]
3.Prosiri polje Q(16^(1/3))
--------
POTPITANJA:
Lagrangeov tm
Euklidova domena/prsten
Gaussovi brojevi
za koje prstenove se poklapa pojam ireducibilan i max (tm o djeljenju s ostatkom)
Kakav je gl ideal nad ireducibilnim elem?
Koliko ima grupa reda 15,a reda 6?
Koja je razlika u prosirenju polja Q(2,5), Q(2*5)?
Sve Abelove grupe reda 36
Sta je faktorij. prsten a nije domena gl ideala?
Centar grupe, kada je normalna, sta je Z\Z(G)?
Sretno!
Moja pitanja:
1. Što znate reći o centru grupe?
Kakva je to grupa? (normalna podgrupa)
Da li centar može biti jednak cijeloj grupi? (da, kada je grupa Abelova)
2. Koliko ima Abelovih grupa reda 72? (6, treba sve raspisati po teoremu o konačno generiranim Abelovim grupama)Koja od njih je izomorfna grupi Z72?
3.Kada je grupa prosta? ( kada nema pravih normalnih podgrupa)
4. Primjer faktorijalne domene koja nije domena glavnih ideala. ( Z[x] - treba o tome pričati, zašto to nije domena glavnih ideala, može biti generirana s dva elementa(?), pokazati to....)
5.Proširenje Q( 3^(1/2) )! Dimenzija ovog polja! Kako znamo kolika je? Minimalni polinom, kakav je (ireducibilan). Koja je baza?
Savjet: Učite primjere! Profesor traži razumijevanje teorema na primjerima. Ja sam se kod učenja više koncentrirala na to da dobro naučim sve iskaze, pa se nisam baš proslavila (iako sam prošla).
Dokaze ne trebate, ali primjere OBAVEZNO!!
-----------------------------------------------------------------------
Pitanja drugih ljudi (zapisala vifi  ) : ) :
1.Cauchieva lema (Tm XXXVI)
Prvi Silovljev tm
-zasto je lema bitna za 1 Silovljev tm
2.prost ideal,ireducibilan ideal, max i prost element
- ko koga povlaci i kada je ekvivalentno
3.Kako prosiriti polje Q( 2^(1/2) , 5^(1/3) ) ?
-objasniti kako to polje izgleda i kolika mu je duljina
---------
1.Tm o konacno generiranim Abelovim grupama
2.Razlika kod prstena, koja je struktura Z[x], Q[x] F[x]
3.Prosiri polje Q(16^(1/3))
--------
POTPITANJA:
Lagrangeov tm
Euklidova domena/prsten
Gaussovi brojevi
za koje prstenove se poklapa pojam ireducibilan i max (tm o djeljenju s ostatkom)
Kakav je gl ideal nad ireducibilnim elem?
Koliko ima grupa reda 15,a reda 6?
Koja je razlika u prosirenju polja Q(2,5), Q(2*5)?
Sve Abelove grupe reda 36
Sta je faktorij. prsten a nije domena gl ideala?
Centar grupe, kada je normalna, sta je Z\Z(G)?
Sretno!
_________________
Ispravite me, ako griješim!
|
|
| [Vrh] |
|
Gost
|
 Postano: 19:22 čet, 13. 7. 2006 Naslov: Postano: 19:22 čet, 13. 7. 2006 Naslov: |
    |
|
|
Danasnja pitanja su bila:
1. neka je red grupe G p. Treba dokazati da je prosta i da je izomorfna grupi Z p.
2. R komutativan prsten, i R^2=R. Treba dokazati da je svaki max. ideal i prost.
Kad vrijedi ireducibilan element = prost??
3.Dokazi da je jednako: Q(2^1/2,3^1/3) i Q(2^1/2*3^1/3)
Taj dio je svima isti.... pise se, i onda proziva jednog po jednog, i ispituje dodatna pitanja, uglavnom ono sto nismo napisali.
Sretno!
Danasnja pitanja su bila:
1. neka je red grupe G p. Treba dokazati da je prosta i da je izomorfna grupi Z p.
2. R komutativan prsten, i R^2=R. Treba dokazati da je svaki max. ideal i prost.
Kad vrijedi ireducibilan element = prost??
3.Dokazi da je jednako: Q(2^1/2,3^1/3) i Q(2^1/2*3^1/3)
Taj dio je svima isti.... pise se, i onda proziva jednog po jednog, i ispituje dodatna pitanja, uglavnom ono sto nismo napisali.
Sretno!
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
hermione
Forumaš(ica)


Pridružen/a: 23. 09. 2003. (10:50:57)
Postovi: (152)16
Spol: 
Sarma: -
|
 Postano: 13:17 uto, 26. 9. 2006 Naslov: Postano: 13:17 uto, 26. 9. 2006 Naslov: |
    |
|
|
Usmeni 26.09.2006.g.
1. Konacno generirane Abelove grupe(tm, neki primjer)
2. Prsten glavnih ideala, ireducibilan element ekviv. prostom elementu, kada, koji uvjeti, raspisati sve ....
3. Prosirenje polja [latex]\mathbb{Z}_p[/latex] (neki primjer koji hocete objasnite)
Profesor tocno kaze sta hoce da mu se napise u kojem pitanju i kao sto je vec napisano, poslije ulazite jedan po jedan i profesor postavi koje podpitanje i to je to.
Usmeni 26.09.2006.g.
1. Konacno generirane Abelove grupe(tm, neki primjer)
2. Prsten glavnih ideala, ireducibilan element ekviv. prostom elementu, kada, koji uvjeti, raspisati sve ....
3. Prosirenje polja 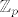 (neki primjer koji hocete objasnite) (neki primjer koji hocete objasnite)
Profesor tocno kaze sta hoce da mu se napise u kojem pitanju i kao sto je vec napisano, poslije ulazite jedan po jedan i profesor postavi koje podpitanje i to je to.
|
|
| [Vrh] |
|
Martinab
Moderator

Pridružen/a: 02. 04. 2003. (19:07:56)
Postovi: (2A03E)16
|
|
| [Vrh] |
|
frrr
Forumaš(ica)

Pridružen/a: 14. 04. 2004. (19:17:12)
Postovi: (47)16
Lokacija: Winterfell
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
Martinab
Moderator

Pridružen/a: 02. 04. 2003. (19:07:56)
Postovi: (2A03E)16
|
 Postano: 1:38 čet, 5. 10. 2006 Naslov: Postano: 1:38 čet, 5. 10. 2006 Naslov: |
    |
|
|
Hm... Da vidimo. Mozda bolje da ovo pise netko tko je to slusao sad i da objasni na nacin na koji je pokazano na predavanjima, ali... I'll give it a go.
Dakle, polje F(a,b,c) je polje koje dobijes tako da polju F dodas elemente a,b,c. Zbog ovog zahtjeva da je polje, mora, osim a,b,c, sadrzavati i sve sto mozes dobiti njihovim zbrajanjem, oduzimanjem, mnozenjem, dijeljenjem s drugim elementima polja i medusobno. Na primjer polje Q(2^(1/2)) je potpolje od R koje se dobije kad se polju Q doda drugi korijen iz dva. Tada ono, osim Q i a=2^(1/2), mora sadrzavati i a^2, a^3 i td, zatim inverze tih elemenata a^-1, a^-2, itd, i sve linearne kombinacije tih elemenata sa koeficijentima iz Q. Kad pogledas kak izgledaju sve te potencije, ispada da je a^0=1, a^1=2^(1/2), a^2=2, sto je iz Q. Dalje se sve vece potencije mogu napisati kao nesto iz Q ili nesto iz Q puta 2^(1/2). Jos uzmes u obzir i zbrajanje, i ispada da tvoj Q(2^(1/2)) mora sadrzavati sve elemente oblika q+r2^(1/2), sa q i r iz Q. Ako sad pogledas kako izgledaju inverzi tih elemenata 1/(q+r2^(1/2)) da vidis da li mozda i njih moras ubaciti u polje, nakon kratkog racuna (racionaliziras nazivnik ko u srednjoj skoli), ispada da su oni vec tog istog oblika. Dakle, skup svih q+r2^(1/2), kad q i r prolaze po skupu racionalnih brojeva, je zatvoren na oduzimanje i dijeljenje el.razl. od 0, pa je stvarno potpolje od R, a zbog gornjih komentara to je i najmanje potpolje od R koje sadrzi i Q i korjen iz dva.
Tak bi islo i za druge brojeve koji su algebarski nad Q (nultocke polinoma s koef iz Q). Malo je drukcija situacija s onima koji nisu, npr. pi. Q(pi) bi trebao imati pi, pi^2, pi^3 itd, i nijedan od njih ne bi bio iz Q ili se mogao izraziti preko prethodnih. Onda bi tu jos trebalo dodati sve inverze, pa sve inverze od suma tih elemenata, i situacija bi se generalno zakomplicirala.
[quote="Anonymous"]Može li mi netko napisati kako se rješavaju zadaci:
1. Kako prosiriti polje Q( 2^(1/2) , 5^(1/3) ) ?
-objasniti kako to polje izgleda i kolika mu je duljina [/quote]
Ovo je krivo pitanje. Polje Q( 2^(1/2) , 5^(1/3)) se moze prosioriti na neprebrojivo mnogo nacina, i ne vjerujem da je to bilo pitanje :) Kako izgleda polje Q( 2^(1/2) , 5^(1/3)), ili kako prosiriti polje Q sa elementima 2^(1/2) i 5^(1/3) je vjerojatno kako je glasilo. Pogledaj ovako: da dodajemo samo 2^(1/2), dobili bi ono sto sam napisala gore (linerane kombinacije nad Q elemenata 1 i 2^(1/2)). Da dodajemo samo b=5^(1/3), dobili bi slicno, ali bi tek trecu potenciju b bilo moguce izraziti preko prethodnih. Zato bi dobili da je Q(5^(1/3)) skup svih lin komb nad Q od 1, 5^(1/3) i 5^(2/3). E sad, kad dodajes oba elementa, onda moras dodati i sve medusobne produkte tih- dakle, ukupno 2*3 elemenata baze (1, 5^(1/3), 5^(2/3), 2^(1/2), 5^(1/3)2^(1/2), 5^(2/3)2^(1/2) ).
[quote]2. Koja je razlika u prosirenju polja Q(2,5), Q(2*5)? [/quote]
Hm... Nikakva? I 2, i 5, i 2*5 su u Q, i prosirenjei Q s njima nema nikakvog efekta. Jel ovo pitanje mozda trebalo skroz drukcije zvucat?
Hm... Da vidimo. Mozda bolje da ovo pise netko tko je to slusao sad i da objasni na nacin na koji je pokazano na predavanjima, ali... I'll give it a go.
Dakle, polje F(a,b,c) je polje koje dobijes tako da polju F dodas elemente a,b,c. Zbog ovog zahtjeva da je polje, mora, osim a,b,c, sadrzavati i sve sto mozes dobiti njihovim zbrajanjem, oduzimanjem, mnozenjem, dijeljenjem s drugim elementima polja i medusobno. Na primjer polje Q(2^(1/2)) je potpolje od R koje se dobije kad se polju Q doda drugi korijen iz dva. Tada ono, osim Q i a=2^(1/2), mora sadrzavati i a^2, a^3 i td, zatim inverze tih elemenata a^-1, a^-2, itd, i sve linearne kombinacije tih elemenata sa koeficijentima iz Q. Kad pogledas kak izgledaju sve te potencije, ispada da je a^0=1, a^1=2^(1/2), a^2=2, sto je iz Q. Dalje se sve vece potencije mogu napisati kao nesto iz Q ili nesto iz Q puta 2^(1/2). Jos uzmes u obzir i zbrajanje, i ispada da tvoj Q(2^(1/2)) mora sadrzavati sve elemente oblika q+r2^(1/2), sa q i r iz Q. Ako sad pogledas kako izgledaju inverzi tih elemenata 1/(q+r2^(1/2)) da vidis da li mozda i njih moras ubaciti u polje, nakon kratkog racuna (racionaliziras nazivnik ko u srednjoj skoli), ispada da su oni vec tog istog oblika. Dakle, skup svih q+r2^(1/2), kad q i r prolaze po skupu racionalnih brojeva, je zatvoren na oduzimanje i dijeljenje el.razl. od 0, pa je stvarno potpolje od R, a zbog gornjih komentara to je i najmanje potpolje od R koje sadrzi i Q i korjen iz dva.
Tak bi islo i za druge brojeve koji su algebarski nad Q (nultocke polinoma s koef iz Q). Malo je drukcija situacija s onima koji nisu, npr. pi. Q(pi) bi trebao imati pi, pi^2, pi^3 itd, i nijedan od njih ne bi bio iz Q ili se mogao izraziti preko prethodnih. Onda bi tu jos trebalo dodati sve inverze, pa sve inverze od suma tih elemenata, i situacija bi se generalno zakomplicirala.
| Anonymous (napisa): | Može li mi netko napisati kako se rješavaju zadaci:
1. Kako prosiriti polje Q( 2^(1/2) , 5^(1/3) ) ?
-objasniti kako to polje izgleda i kolika mu je duljina |
Ovo je krivo pitanje. Polje Q( 2^(1/2) , 5^(1/3)) se moze prosioriti na neprebrojivo mnogo nacina, i ne vjerujem da je to bilo pitanje  Kako izgleda polje Q( 2^(1/2) , 5^(1/3)), ili kako prosiriti polje Q sa elementima 2^(1/2) i 5^(1/3) je vjerojatno kako je glasilo. Pogledaj ovako: da dodajemo samo 2^(1/2), dobili bi ono sto sam napisala gore (linerane kombinacije nad Q elemenata 1 i 2^(1/2)). Da dodajemo samo b=5^(1/3), dobili bi slicno, ali bi tek trecu potenciju b bilo moguce izraziti preko prethodnih. Zato bi dobili da je Q(5^(1/3)) skup svih lin komb nad Q od 1, 5^(1/3) i 5^(2/3). E sad, kad dodajes oba elementa, onda moras dodati i sve medusobne produkte tih- dakle, ukupno 2*3 elemenata baze (1, 5^(1/3), 5^(2/3), 2^(1/2), 5^(1/3)2^(1/2), 5^(2/3)2^(1/2) ). Kako izgleda polje Q( 2^(1/2) , 5^(1/3)), ili kako prosiriti polje Q sa elementima 2^(1/2) i 5^(1/3) je vjerojatno kako je glasilo. Pogledaj ovako: da dodajemo samo 2^(1/2), dobili bi ono sto sam napisala gore (linerane kombinacije nad Q elemenata 1 i 2^(1/2)). Da dodajemo samo b=5^(1/3), dobili bi slicno, ali bi tek trecu potenciju b bilo moguce izraziti preko prethodnih. Zato bi dobili da je Q(5^(1/3)) skup svih lin komb nad Q od 1, 5^(1/3) i 5^(2/3). E sad, kad dodajes oba elementa, onda moras dodati i sve medusobne produkte tih- dakle, ukupno 2*3 elemenata baze (1, 5^(1/3), 5^(2/3), 2^(1/2), 5^(1/3)2^(1/2), 5^(2/3)2^(1/2) ).
| Citat: | | 2. Koja je razlika u prosirenju polja Q(2,5), Q(2*5)? |
Hm... Nikakva? I 2, i 5, i 2*5 su u Q, i prosirenjei Q s njima nema nikakvog efekta. Jel ovo pitanje mozda trebalo skroz drukcije zvucat?
_________________
A comathematician is a device for turning cotheorems into ffee. A cotheorem is, naturally, an easy nsequence of a rollary.
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
zara
Forumaš(ica)


Pridružen/a: 14. 02. 2004. (17:59:26)
Postovi: (4)16
|
|
| [Vrh] |
|
Lara
Forumaš(ica)


Pridružen/a: 17. 01. 2007. (16:23:54)
Postovi: (53)16
Spol: 
|
|
| [Vrh] |
|
Marko
Forumaš(ica)


Pridružen/a: 16. 06. 2004. (11:05:48)
Postovi: (71)16
Spol: 
|
|
| [Vrh] |
|
Red Rose
Forumaš(ica)

Pridružen/a: 04. 08. 2009. (15:28:09)
Postovi: (1)16
Lokacija: Berlin
|
|
| [Vrh] |
|
Feanor
Forumaš(ica)

Pridružen/a: 15. 11. 2005. (18:18:15)
Postovi: (27)16
Spol: 
Lokacija: Zagreb/Bjelovar
|
|
| [Vrh] |
|
sunce
Forumaš(ica)

Pridružen/a: 20. 03. 2010. (18:49:03)
Postovi: (3F)16
|
|
| [Vrh] |
|
piper at the gates
Forumaš(ica)

Pridružen/a: 14. 03. 2009. (20:02:03)
Postovi: (1F)16
Spol: 
|
|
| [Vrh] |
|
Crvenkapica
Forumaš(ica)

Pridružen/a: 16. 04. 2007. (14:52:45)
Postovi: (AB)16
|
 Postano: 1:03 sri, 30. 6. 2010 Naslov: Postano: 1:03 sri, 30. 6. 2010 Naslov: |
    |
|
|
Da pita dokaze, znam da je pitao teoreme i dokaze za Lagrangea, Kvocijentne grupe, dio Prvog teorema o izomorfizmu za grupe (koji dio ne znam), rekle mi frendice. Ako ništa drugo nauči ove glavne teoreme i njihove dokaze, ako za dva ogovaraš sumnjam da će te ispitivati neke bijesne teoreme i dokaze. Sretno.
Da pita dokaze, znam da je pitao teoreme i dokaze za Lagrangea, Kvocijentne grupe, dio Prvog teorema o izomorfizmu za grupe (koji dio ne znam), rekle mi frendice. Ako ništa drugo nauči ove glavne teoreme i njihove dokaze, ako za dva ogovaraš sumnjam da će te ispitivati neke bijesne teoreme i dokaze. Sretno.
|
|
| [Vrh] |
|
mmvvooll
Forumaš(ica)

Pridružen/a: 21. 02. 2009. (19:16:06)
Postovi: (16)16
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
|









