| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
Bubsi
Forumaš(ica)

Pridružen/a: 10. 11. 2008. (17:18:35)
Postovi: (4A)16
Spol: 
Lokacija: Split
|
|
| [Vrh] |
|
ivanak1111
Forumaš(ica)

Pridružen/a: 28. 03. 2007. (17:57:37)
Postovi: (22)16
|
|
| [Vrh] |
|
Bubsi
Forumaš(ica)

Pridružen/a: 10. 11. 2008. (17:18:35)
Postovi: (4A)16
Spol: 
Lokacija: Split
|
|
| [Vrh] |
|
Iv
Forumaš(ica)

Pridružen/a: 16. 02. 2007. (00:16:42)
Postovi: (1E)16
Spol: 
|
|
| [Vrh] |
|
Bug
Forumaš(ica)


Pridružen/a: 06. 04. 2003. (17:31:11)
Postovi: (1A9)16
Spol: 
Lokacija: Kako kad!!
|
|
| [Vrh] |
|
ecan
Forumaš(ica)

Pridružen/a: 01. 06. 2010. (18:09:54)
Postovi: (23)16
|
|
| [Vrh] |
|
Bug
Forumaš(ica)


Pridružen/a: 06. 04. 2003. (17:31:11)
Postovi: (1A9)16
Spol: 
Lokacija: Kako kad!!
|
|
| [Vrh] |
|
romkinja
Forumaš(ica)
Pridružen/a: 08. 11. 2007. (19:07:37)
Postovi: (B)16
|
|
| [Vrh] |
|
goranm
Forumaš(ica)


Pridružen/a: 12. 11. 2002. (20:09:12)
Postovi: (906)16
Spol: 
|
 Postano: 20:39 pon, 2. 7. 2012 Naslov: Postano: 20:39 pon, 2. 7. 2012 Naslov: |
    |
|
|
[quote="romkinja"]Može pomoć oko 1. zadatka iz 1.kolokvija? Jeste u zadatku raspisivali matrice uz uvjet da je det=1 ili je dovoljno gledati det matrice i riješiti pomoću Binet-Cauchy-a?[/quote]
Dovoljno je koristiti Binet-Cauchyev teorem kako bi se pokazalo da je X grupoid. Množenje kvadratnih matrica je asocijativno pa je X i polugrupa. Jer je jedinična matrica iz X (a=d=1 i b=c=0 su elementi iz [latex]\mathbb{N}_0[/latex]), onda je X monoid. Ali X nije grupa jer npr. [tex]\left(\begin{matrix} 1 & 0 \\ 1 & 1\end{matrix}\right)[/tex] nema inverz u X. Inverz te matrice je [tex]\left(\begin{matrix} 1 & 0 \\ -1 & 1\end{matrix}\right)[/tex], ali -1 nije u [latex]\mathbb{N}_0[/latex].
[quote]Također i 3. zadatak iz 1. kolokvija...
Riješila sam ga ali nisam dobila bodove, pa nisam sigurna zašto.
Ako netko može pomoći?[/quote]
Prvo treba provjeriti da je W podgrupa od G. Očito je W podskup od G jer sve matrice u W imaju determinantu [tex]y\cdot y^{-1}-0\cdot(y-y^{-1})=y\cdot y^{-1}=1[/tex]. Idući korak bi bio provjeriti da za dvije matrice A,B iz W vrijedi da je i [tex]AB^{-1}[/tex] u W. Neka je [tex]A=\left(\begin{matrix} x & 0 \\ x-x^{-1} & x^{-1}\end{matrix}\right)[/tex] te [tex]B=\left(\begin{matrix} y & 0 \\ y-y^{-1} & y^{-1}\end{matrix}\right)[/tex]. Onda je [tex]B^{-1}=\left(\begin{matrix} y^{-1} & 0 \\ -y+y^{-1} & y\end{matrix}\right)[/tex] pa je
[dtex]AB^{-1}=\left(\begin{matrix}
xy^{-1} & 0\\
xy^{-1}-(x y^{-1})^{-1} & x^{-1}y
\end{matrix}\right)=\left(\begin{matrix}
xy^{-1} & 0\\
xy^{-1}-(x y^{-1})^{-1} & (xy^{-1})^{-1}
\end{matrix}\right).[/dtex]
Ovdje je dobro za napomenuti da x i y komutiraju (jer su iz [latex]\mathbb{R}^\times[/latex]) pa da onda možemo lako manipulirati s izrazima poput [latex]x^{-1}y=(y^{-1}x)^{-1}=(xy^{-1})^{-1}[/latex]. Dakle, W je podgrupa od G.
Ostaje za provjeriti da li je W normalna podgrupa od G. Neka je [tex]A=\left(\begin{matrix} a & b \\ c & d\end{matrix}\right)\in G[/tex] te neka je [tex]B=\left(\begin{matrix} y & 0 \\ y-y^{-1} & y^{-1}\end{matrix}\right)\in W[/tex]. Želimo pokazati da je [tex]ABA^{-1}\in W[/tex]. U ovom trenutku ne znam da li to vrijedi za bilo koji izbor matrica A iz G i B iz W, ali zbog toga što matrice u W imaju određen element (1,2), onda mi ne bi bilo nevjerojatno da se nađu matrice A i B td. njihov produkt [tex]ABA^{-1}[/tex] nema na mjestu (1,2) nulu. Za početak ću gledati samo što se nalazi na mjestu (1,2) u produktu [tex]ABA^{-1}[/tex], a to je [tex]y^{-1}b(a+b)(-1+y^2)[/tex]. Sada mi je već jasno da mogu odabrati y, a i b td. je [tex]y^{-1}b(a+b)(-1+y^2)\neq 0[/tex].
Očito mora biti [latex]y\notin\{-1,0,1\}[/latex] pa ću uzeti y=2. Isto, b ne smije biti 0, ali a može. Neka je onda b=1. Lako se provjeri da je [tex]y^{-1}b(a+b)(-1+y^2)\neq 0[/tex]. Sada još trebam naštimati matrice A i B td. je A u G, a B u W.
Jer je a=0, a b=1, onda mora biti c=-1 i d=0 kako bi A bila u G. Matrica B je u potpunosti određena s y pa tu nije potrebno ništa naštimavati. Ostaje za provjeriti da [latex]ABA^{-1}[/latex] nije u W, a to vrijedi jer je
[dtex]ABA^{-1}=\left(\begin{matrix}1/2 & -3/2 \\ 0 & 2\end{matrix}\right).[/dtex]
Dakle, W nije normalna podgrupa grupe G.
| romkinja (napisa): | | Može pomoć oko 1. zadatka iz 1.kolokvija? Jeste u zadatku raspisivali matrice uz uvjet da je det=1 ili je dovoljno gledati det matrice i riješiti pomoću Binet-Cauchy-a? |
Dovoljno je koristiti Binet-Cauchyev teorem kako bi se pokazalo da je X grupoid. Množenje kvadratnih matrica je asocijativno pa je X i polugrupa. Jer je jedinična matrica iz X (a=d=1 i b=c=0 su elementi iz 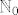 ), onda je X monoid. Ali X nije grupa jer npr. [tex]\left(\begin{matrix} 1 & 0 \\ 1 & 1\end{matrix}\right)[/tex] nema inverz u X. Inverz te matrice je [tex]\left(\begin{matrix} 1 & 0 \\ -1 & 1\end{matrix}\right)[/tex], ali -1 nije u ), onda je X monoid. Ali X nije grupa jer npr. [tex]\left(\begin{matrix} 1 & 0 \\ 1 & 1\end{matrix}\right)[/tex] nema inverz u X. Inverz te matrice je [tex]\left(\begin{matrix} 1 & 0 \\ -1 & 1\end{matrix}\right)[/tex], ali -1 nije u 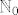 . .
| Citat: | Također i 3. zadatak iz 1. kolokvija...
Riješila sam ga ali nisam dobila bodove, pa nisam sigurna zašto.
Ako netko može pomoći? |
Prvo treba provjeriti da je W podgrupa od G. Očito je W podskup od G jer sve matrice u W imaju determinantu [tex]y\cdot y^{-1}-0\cdot(y-y^{-1})=y\cdot y^{-1}=1[/tex]. Idući korak bi bio provjeriti da za dvije matrice A,B iz W vrijedi da je i [tex]AB^{-1}[/tex] u W. Neka je [tex]A=\left(\begin{matrix} x & 0 \\ x-x^{-1} & x^{-1}\end{matrix}\right)[/tex] te [tex]B=\left(\begin{matrix} y & 0 \\ y-y^{-1} & y^{-1}\end{matrix}\right)[/tex]. Onda je [tex]B^{-1}=\left(\begin{matrix} y^{-1} & 0 \\ -y+y^{-1} & y\end{matrix}\right)[/tex] pa je
[dtex]AB^{-1}=\left(\begin{matrix}
xy^{-1} & 0\\
xy^{-1}-(x y^{-1})^{-1} & x^{-1}y
\end{matrix}\right)=\left(\begin{matrix}
xy^{-1} & 0\\
xy^{-1}-(x y^{-1})^{-1} & (xy^{-1})^{-1}
\end{matrix}\right).[/dtex]
Ovdje je dobro za napomenuti da x i y komutiraju (jer su iz 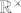 ) pa da onda možemo lako manipulirati s izrazima poput ) pa da onda možemo lako manipulirati s izrazima poput 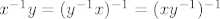 . Dakle, W je podgrupa od G. . Dakle, W je podgrupa od G.
Ostaje za provjeriti da li je W normalna podgrupa od G. Neka je [tex]A=\left(\begin{matrix} a & b \\ c & d\end{matrix}\right)\in G[/tex] te neka je [tex]B=\left(\begin{matrix} y & 0 \\ y-y^{-1} & y^{-1}\end{matrix}\right)\in W[/tex]. Želimo pokazati da je [tex]ABA^{-1}\in W[/tex]. U ovom trenutku ne znam da li to vrijedi za bilo koji izbor matrica A iz G i B iz W, ali zbog toga što matrice u W imaju određen element (1,2), onda mi ne bi bilo nevjerojatno da se nađu matrice A i B td. njihov produkt [tex]ABA^{-1}[/tex] nema na mjestu (1,2) nulu. Za početak ću gledati samo što se nalazi na mjestu (1,2) u produktu [tex]ABA^{-1}[/tex], a to je [tex]y^{-1}b(a+b)(-1+y^2)[/tex]. Sada mi je već jasno da mogu odabrati y, a i b td. je [tex]y^{-1}b(a+b)(-1+y^2)\neq 0[/tex].
Očito mora biti 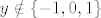 pa ću uzeti y=2. Isto, b ne smije biti 0, ali a može. Neka je onda b=1. Lako se provjeri da je [tex]y^{-1}b(a+b)(-1+y^2)\neq 0[/tex]. Sada još trebam naštimati matrice A i B td. je A u G, a B u W. pa ću uzeti y=2. Isto, b ne smije biti 0, ali a može. Neka je onda b=1. Lako se provjeri da je [tex]y^{-1}b(a+b)(-1+y^2)\neq 0[/tex]. Sada još trebam naštimati matrice A i B td. je A u G, a B u W.
Jer je a=0, a b=1, onda mora biti c=-1 i d=0 kako bi A bila u G. Matrica B je u potpunosti određena s y pa tu nije potrebno ništa naštimavati. Ostaje za provjeriti da 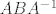 nije u W, a to vrijedi jer je nije u W, a to vrijedi jer je
[dtex]ABA^{-1}=\left(\begin{matrix}1/2 & -3/2 \\ 0 & 2\end{matrix}\right).[/dtex]
Dakle, W nije normalna podgrupa grupe G.
_________________
The Dude Abides
|
|
| [Vrh] |
|
romkinja
Forumaš(ica)
Pridružen/a: 08. 11. 2007. (19:07:37)
Postovi: (B)16
|
|
| [Vrh] |
|
ivy=)
Forumaš(ica)
Pridružen/a: 03. 11. 2007. (14:00:45)
Postovi: (34)16
|
|
| [Vrh] |
|
goranm
Forumaš(ica)


Pridružen/a: 12. 11. 2002. (20:09:12)
Postovi: (906)16
Spol: 
|
 Postano: 12:58 uto, 3. 7. 2012 Naslov: Postano: 12:58 uto, 3. 7. 2012 Naslov: |
    |
|
|
[quote="ivy=)"]ja bi molila pomoc oko 2. zadatka iz prvog kolokvija, konkretno ovaj epimorfizam, izgubila sam bodove pa ne znam sto je krivo[/quote]
Trebamo provjeriti da za svaki (a,b) iz [latex]\mathbb{Z}^2[/latex] postoji (x,y,z) iz [latex]\mathbb{Z}^3[/latex] td. je f(x,y,z)=(a,b), odnosno da sustav
[dtex]\begin{eqnarray}x+2y+3z=a,\\
z-x-y=b,\end{eqnarray}[/dtex]
ima barem jedno rješenje u [latex]\mathbb{Z}^3[/latex]. Dakle, ne zanima me čitava klasa rješenja, nego samo da li postoji uopće jedno za bilo koji izbor cijelih brojeva a i b.
Odabrati ću z=0 i vidjeti da li postoje cijeli brojevi x i y td. sustav
[dtex]\begin{eqnarray}x+2y=a,\\
-x-y=b,\end{eqnarray}[/dtex]
ima rješenje. Očito je x=-a-2b, a y=a+b i to su cijeli brojevi. Dakle, za bilo koju točku (a,b) iz [latex]\mathbb{Z}^2[/latex] odabirom točke (-a-2b,a+b,0) iz [latex]\mathbb{Z}^3[/latex] zaključujemo da vrijedi f(-a-2b,a+b,0)=(a,b), što znači da je f surjekcija pa je i epimorfizam.
| ivy=) (napisa): | | ja bi molila pomoc oko 2. zadatka iz prvog kolokvija, konkretno ovaj epimorfizam, izgubila sam bodove pa ne znam sto je krivo |
Trebamo provjeriti da za svaki (a,b) iz 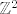 postoji (x,y,z) iz postoji (x,y,z) iz 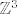 td. je f(x,y,z)=(a,b), odnosno da sustav td. je f(x,y,z)=(a,b), odnosno da sustav
[dtex]\begin{eqnarray}x+2y+3z=a,\\
z-x-y=b,\end{eqnarray}[/dtex]
ima barem jedno rješenje u 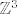 . Dakle, ne zanima me čitava klasa rješenja, nego samo da li postoji uopće jedno za bilo koji izbor cijelih brojeva a i b. . Dakle, ne zanima me čitava klasa rješenja, nego samo da li postoji uopće jedno za bilo koji izbor cijelih brojeva a i b.
Odabrati ću z=0 i vidjeti da li postoje cijeli brojevi x i y td. sustav
[dtex]\begin{eqnarray}x+2y=a,\\
-x-y=b,\end{eqnarray}[/dtex]
ima rješenje. Očito je x=-a-2b, a y=a+b i to su cijeli brojevi. Dakle, za bilo koju točku (a,b) iz 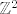 odabirom točke (-a-2b,a+b,0) iz odabirom točke (-a-2b,a+b,0) iz 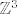 zaključujemo da vrijedi f(-a-2b,a+b,0)=(a,b), što znači da je f surjekcija pa je i epimorfizam. zaključujemo da vrijedi f(-a-2b,a+b,0)=(a,b), što znači da je f surjekcija pa je i epimorfizam.
_________________
The Dude Abides
|
|
| [Vrh] |
|
ivy=)
Forumaš(ica)
Pridružen/a: 03. 11. 2007. (14:00:45)
Postovi: (34)16
|
|
| [Vrh] |
|
Bug
Forumaš(ica)


Pridružen/a: 06. 04. 2003. (17:31:11)
Postovi: (1A9)16
Spol: 
Lokacija: Kako kad!!
|
|
| [Vrh] |
|
goranm
Forumaš(ica)


Pridružen/a: 12. 11. 2002. (20:09:12)
Postovi: (906)16
Spol: 
|
 Postano: 19:38 uto, 3. 7. 2012 Naslov: Postano: 19:38 uto, 3. 7. 2012 Naslov: |
    |
|
|
[quote="ivy=)"]a i ako ima neka dobra dusa da rijesi 4. zadatka iz drugog kolokvija[/quote]
Da je M potprsten pokazuje se tako da se primijeti da je [tex]m^2=\overline{m}=-1-m[/tex].
Pretpostavimo da je [tex]g\colon M \to \mathbb{R}[/tex] homomorfizam prstena za kojeg vrijedi g(1)=1. Uvjet g(1)=1 u potpunosti određuje g na cijelim brojevima, tj. za [tex]n\in\mathbb{N}[/tex] vrijedi
[dtex]g(n)=g(\underbrace{1+\cdots + 1}_{\textrm{n puta}})=(\textrm{g je homomorfizam})=\underbrace{g(1)+\cdots+g(1)}_{\textrm{n puta}}=\underbrace{1+\cdots+1}_{\textrm{n puta}}=n,[/dtex]
a, naravno, ako je n negativan cijeli broj, onda postoji pozitivan cijeli broj m td. je n=-m pa je g(n)=g(-m)=-g(m)=-m=n. Iz istog razloga za svaki cijeli broj b vrijedi g(bm)=bg(m).
Prema tome, za a+bm iz M vrijedi
[dtex]g(a+bm)=g((a+0\cdot m)+(0+bm))=(\textrm{g je homomorfizam})=g(a+0\cdot m)+g(0+bm)=g(a)+g(bm)=a+bg(m).[/dtex]
To su jedine informacije o tom homomorfizmu koje možemo izvući, a jedina preostala stvar koju znamo je da vrijedi [tex]m^2=\overline{m}=-1-m[/tex]. Pogledati ćemo koliko je [tex]g(m^2)\colon[/tex]
[dtex]g(m^2)=g(\overline{m})=g(-1-m)=-1-g(m).[/dtex]
Jer je g homomorfizam, onda je [tex]g(m^2)=g(m)^2[/tex] pa imamo
[dtex]g(m)^2+g(m)+1=0.[/dtex]
Prethodno je kvadratna jednadžba čija je diskriminanta jednaka -3, tj. g(m) je broj u [tex]\mathbb{C}\setminus\mathbb{R}[/tex] što je kontradikcija s pretpostavkom da je g homomorfizam s kodomenom [tex]\mathbb{R}[/tex].
| ivy=) (napisa): | | a i ako ima neka dobra dusa da rijesi 4. zadatka iz drugog kolokvija |
Da je M potprsten pokazuje se tako da se primijeti da je [tex]m^2=\overline{m}=-1-m[/tex].
Pretpostavimo da je [tex]g\colon M \to \mathbb{R}[/tex] homomorfizam prstena za kojeg vrijedi g(1)=1. Uvjet g(1)=1 u potpunosti određuje g na cijelim brojevima, tj. za [tex]n\in\mathbb{N}[/tex] vrijedi
[dtex]g(n)=g(\underbrace{1+\cdots + 1}_{\textrm{n puta}})=(\textrm{g je homomorfizam})=\underbrace{g(1)+\cdots+g(1)}_{\textrm{n puta}}=\underbrace{1+\cdots+1}_{\textrm{n puta}}=n,[/dtex]
a, naravno, ako je n negativan cijeli broj, onda postoji pozitivan cijeli broj m td. je n=-m pa je g(n)=g(-m)=-g(m)=-m=n. Iz istog razloga za svaki cijeli broj b vrijedi g(bm)=bg(m).
Prema tome, za a+bm iz M vrijedi
[dtex]g(a+bm)=g((a+0\cdot m)+(0+bm))=(\textrm{g je homomorfizam})=g(a+0\cdot m)+g(0+bm)=g(a)+g(bm)=a+bg(m).[/dtex]
To su jedine informacije o tom homomorfizmu koje možemo izvući, a jedina preostala stvar koju znamo je da vrijedi [tex]m^2=\overline{m}=-1-m[/tex]. Pogledati ćemo koliko je [tex]g(m^2)\colon[/tex]
[dtex]g(m^2)=g(\overline{m})=g(-1-m)=-1-g(m).[/dtex]
Jer je g homomorfizam, onda je [tex]g(m^2)=g(m)^2[/tex] pa imamo
[dtex]g(m)^2+g(m)+1=0.[/dtex]
Prethodno je kvadratna jednadžba čija je diskriminanta jednaka -3, tj. g(m) je broj u [tex]\mathbb{C}\setminus\mathbb{R}[/tex] što je kontradikcija s pretpostavkom da je g homomorfizam s kodomenom [tex]\mathbb{R}[/tex].
_________________
The Dude Abides
|
|
| [Vrh] |
|
Serious Sam
Forumaš(ica)


Pridružen/a: 09. 12. 2009. (15:08:32)
Postovi: (5C)16
Spol: 
|
|
| [Vrh] |
|
marlen
Forumaš(ica)


Pridružen/a: 01. 11. 2007. (23:42:26)
Postovi: (57)16
Lokacija: MedVEšČak
|
 Postano: 8:09 sri, 4. 7. 2012 Naslov: Postano: 8:09 sri, 4. 7. 2012 Naslov: |
    |
|
|
[quote="Serious Sam"]Jel zna tko objasniti jel postoje neki netrivijalni ideali u prstenu kao sto smo imali u 2. zadatku 2. kolokvija ove godine ili 5. zadatak od popravnog prosle godine? Mislim da nije dobra stvar da se provjeravaju moguće kombinacije jer toga ima jako puno onda.[/quote]
evo ja sam na tom zadatku dobila sve bodove pa je valjda to točno.
Pronašla sam ideal i pokazala da je on različiti od nul-ideala i samog prstnena.
Prsten je bil zadani skup 2x2 matrica sa elementima iz skupa cijelih brojeva a na sporednoj dijagonali bili su višekratnici broja 6 i 3.
Za ideal sam uzela skup matrica koji opet na sporednoj dijagonali ima višekratnike brojeva 6 i 3, a na glavnoj dijagonali višekratnike broja 2.
(Znači elementi su mi bili 2x, 6y, 3z, 2t, pri čemu su x,y,z,t iz Z)
Za tako definiran podskup, provjeriti prvo treba da je potprsten, zatim da je ideal.
Napisala sam i (nekom svojom logikom) zašto je on različiti od nul-ideala i nadprstena.
| Serious Sam (napisa): | | Jel zna tko objasniti jel postoje neki netrivijalni ideali u prstenu kao sto smo imali u 2. zadatku 2. kolokvija ove godine ili 5. zadatak od popravnog prosle godine? Mislim da nije dobra stvar da se provjeravaju moguće kombinacije jer toga ima jako puno onda. |
evo ja sam na tom zadatku dobila sve bodove pa je valjda to točno.
Pronašla sam ideal i pokazala da je on različiti od nul-ideala i samog prstnena.
Prsten je bil zadani skup 2x2 matrica sa elementima iz skupa cijelih brojeva a na sporednoj dijagonali bili su višekratnici broja 6 i 3.
Za ideal sam uzela skup matrica koji opet na sporednoj dijagonali ima višekratnike brojeva 6 i 3, a na glavnoj dijagonali višekratnike broja 2.
(Znači elementi su mi bili 2x, 6y, 3z, 2t, pri čemu su x,y,z,t iz Z)
Za tako definiran podskup, provjeriti prvo treba da je potprsten, zatim da je ideal.
Napisala sam i (nekom svojom logikom) zašto je on različiti od nul-ideala i nadprstena.
_________________
u Meni vLaDa LudiLO
|
|
| [Vrh] |
|
GODIMENTI
Forumaš(ica)
Pridružen/a: 15. 02. 2011. (13:15:40)
Postovi: (9)16
|
|
| [Vrh] |
|
goranm
Forumaš(ica)


Pridružen/a: 12. 11. 2002. (20:09:12)
Postovi: (906)16
Spol: 
|
 Postano: 13:02 sri, 4. 7. 2012 Naslov: Postano: 13:02 sri, 4. 7. 2012 Naslov: |
    |
|
|
[quote="Serious Sam"]Jel zna tko objasniti jel postoje neki netrivijalni ideali u prstenu kao sto smo imali u 2. zadatku 2. kolokvija ove godine ili 5. zadatak od popravnog prosle godine? Mislim da nije dobra stvar da se provjeravaju moguće kombinacije jer toga ima jako puno onda.[/quote]
Ako se traži samo egzistencija, bez konkretnog primjera, onda se možeš pozvati na činjenicu da u svakom prstenu s jedinicom postoji maksimalan ideal. Tu onda samo trebaš provjeriti da (0) nije maksimalan ideal.
[quote="GODIMENTI"]Ja bih molila ako može 1. i 3. zadatak iz 2.kolokvija.[/quote]
1. zadatak. Treba provjeriti da za [tex]x_1,x_2,y_1,y_2\in\mathbb{Z}[\sqrt 2][/tex] vrijedi [tex](x_1+iy_1\sqrt 3)-(x_2+iy_2\sqrt 3)\in X[/tex] i [tex](x_1+iy_1\sqrt 3)\cdot(x_2+iy_2\sqrt 3)\in X[/tex]. Nakon raspisa imamo ovo:
[dtex]\begin{eqnarray}(x_1+iy_1\sqrt 3)-(x_2+iy_2\sqrt 3)=(x_1-x_2)+i(y_1-y_2)\sqrt 3,\\(x_1+iy_1\sqrt 3)\cdot(x_2+iy_2\sqrt 3)=x_1x_2-3y_1y_2+i(x_1y_2+x_2y_1)\sqrt 3.\end{eqnarray}[/dtex]Jer je [tex]\mathbb{Z}[\sqrt 2][/tex] prsten, onda su i [tex]x_1-x_2, y_1-y_2, x_1x_2, y_1y_2, x_1y_2[/tex] i [tex]x_2y_1[/tex] elementi u [tex]\mathbb{Z}[\sqrt 2][/tex] pa je X prsten.
Pretpostavimo da X nije integralna domena. Tada postoje [tex]x_1,x_2,y_1,y_2\in\mathbb{Z}[\sqrt 2][/tex] od kojih niti jedan nije 0 i za koje vrijedi [dtex](x_1+iy_1\sqrt 3)\cdot(x_2+iy_2\sqrt 3)=0.[/dtex]Nakon množenja imamo ponovo [dtex](x_1+iy_1\sqrt 3)\cdot(x_2+iy_2\sqrt 3)=x_1x_2-3y_1y_2+i(x_1y_2+x_2y_1)\sqrt 3=0,[/dtex]a iz toga zaključujemo [dtex]\begin{eqnarray}x_1x_2=3y_1y_2,\\x_1y_2+x_2y_1=0.\end{eqnarray}[/dtex]Prvu jednadžbu množimo s [tex]x_1y_1[/tex] (to sigurno nije 0 jer [tex]x_1[/tex] i [tex]y_1[/tex] su ne-nul elementi, a [tex]\mathbb{Z}[\sqrt 2][/tex] je integralna domena), a onda zbog druge jednadžbe slijedi [tex]x_1^2x_2y_1=-3y_1^2x_2y_1[/tex], odnosno [dtex](x_1^2+3y_1^2)x_2y_1=0.[/dtex]Prethodno je jednadžba u [tex]\mathbb{Z}[\sqrt 2][/tex]. Ali, [tex]\mathbb{Z}[\sqrt 2][/tex] je integralna domena pa ili je [tex]x_2y_1=0[/tex] (što povlači da je neki od [tex]x_2,y_1[/tex] jednak nuli, a to je suprotno pretpostavci) ili je [tex](x_1^2+3y_1^2)=0[/tex] što opet nije moguće. Prema tome, X je integralna domena.
____________________________________
3. zadatak. Neka je [tex]p(x)=a_0+a_1x+\cdots + a_nx^n \in\mathbb{Z}[x][/tex] polinom stupnja [tex]n\geq 0[/tex]. Onda je [tex]p(7x)=a_0+7a_1+\cdots 7^na_nx^n[/tex] polinom stupnja [tex]n\geq 0[/tex] s cjelobrojnim koeficijentima pa je [tex]p(7x)\in\mathbb{Z}[x][/tex], odnosno F je dobro definirano preslikavanje.
Neka je [tex]q(x)=b_0+b_1x+\cdots + b_mx^m \in\mathbb{Z}[x][/tex] polinom stupnja [tex]m\geq n[/tex] (bez smanjenja općenitosti). Neka je r(x)=p(x)+q(x). Onda je [dtex]\begin{eqnarray}F(r(x))=r(7x)=(a_0+b_0)+7(a_1+b_1)x+\cdots+7^n(a_n+b_n)x^n+7^{n+1}b_{n+1}x^{n+1}+\cdots 7^mb_mx^m=\\
a_0+7a_1x+\cdots + 7^na_nx^n+b_0+b_1x+\cdots + 7^nb_nx^n+7^{n+1}b_{n+1}x^{n+1}+\cdots 7^mb_mx^m=\\
p(7x)+q(7x)=F(p(x))+F(q(x)).\end{eqnarray}[/dtex] Dalje imamo [dtex]F(p(x)q(x))=F(\sum_{k=0}^{m+n}(\sum_{i+j=k}a_ib_j)x^k)=\sum_{k=0}^{m+n}F((\sum_{i+j=k}a_ib_j)x^k)=\sum_{k=0}^{m+n}(\sum_{i+j=k}a_ib_j)(7x)^k.[/dtex]
[dtex]F(p(x))F(q(x))=(\sum_{i=0}^n7^ia_ix^i)(\sum_{j=0}^m7^jb_jx^j)=\sum_{k=0}^{m+n}(\sum_{i+j=k}7^ia_i7^jb_j)x^k=\sum_{k=0}^{m+n}(\sum_{i+j=k}7^{i+j}a_ib_j)x^k=\sum_{k=0}^{m+n}(\sum_{i+j=k}a_ib_j)7^kx^k.[/dtex]
U jezgri tog preslikavanja nalazi se samo 0.
| Serious Sam (napisa): | | Jel zna tko objasniti jel postoje neki netrivijalni ideali u prstenu kao sto smo imali u 2. zadatku 2. kolokvija ove godine ili 5. zadatak od popravnog prosle godine? Mislim da nije dobra stvar da se provjeravaju moguće kombinacije jer toga ima jako puno onda. |
Ako se traži samo egzistencija, bez konkretnog primjera, onda se možeš pozvati na činjenicu da u svakom prstenu s jedinicom postoji maksimalan ideal. Tu onda samo trebaš provjeriti da (0) nije maksimalan ideal.
| GODIMENTI (napisa): | | Ja bih molila ako može 1. i 3. zadatak iz 2.kolokvija. |
1. zadatak. Treba provjeriti da za [tex]x_1,x_2,y_1,y_2\in\mathbb{Z}[\sqrt 2][/tex] vrijedi [tex](x_1+iy_1\sqrt 3)-(x_2+iy_2\sqrt 3)\in X[/tex] i [tex](x_1+iy_1\sqrt 3)\cdot(x_2+iy_2\sqrt 3)\in X[/tex]. Nakon raspisa imamo ovo:
[dtex]\begin{eqnarray}(x_1+iy_1\sqrt 3)-(x_2+iy_2\sqrt 3)=(x_1-x_2)+i(y_1-y_2)\sqrt 3,\\(x_1+iy_1\sqrt 3)\cdot(x_2+iy_2\sqrt 3)=x_1x_2-3y_1y_2+i(x_1y_2+x_2y_1)\sqrt 3.\end{eqnarray}[/dtex]Jer je [tex]\mathbb{Z}[\sqrt 2][/tex] prsten, onda su i [tex]x_1-x_2, y_1-y_2, x_1x_2, y_1y_2, x_1y_2[/tex] i [tex]x_2y_1[/tex] elementi u [tex]\mathbb{Z}[\sqrt 2][/tex] pa je X prsten.
Pretpostavimo da X nije integralna domena. Tada postoje [tex]x_1,x_2,y_1,y_2\in\mathbb{Z}[\sqrt 2][/tex] od kojih niti jedan nije 0 i za koje vrijedi [dtex](x_1+iy_1\sqrt 3)\cdot(x_2+iy_2\sqrt 3)=0.[/dtex]Nakon množenja imamo ponovo [dtex](x_1+iy_1\sqrt 3)\cdot(x_2+iy_2\sqrt 3)=x_1x_2-3y_1y_2+i(x_1y_2+x_2y_1)\sqrt 3=0,[/dtex]a iz toga zaključujemo [dtex]\begin{eqnarray}x_1x_2=3y_1y_2,\\x_1y_2+x_2y_1=0.\end{eqnarray}[/dtex]Prvu jednadžbu množimo s [tex]x_1y_1[/tex] (to sigurno nije 0 jer [tex]x_1[/tex] i [tex]y_1[/tex] su ne-nul elementi, a [tex]\mathbb{Z}[\sqrt 2][/tex] je integralna domena), a onda zbog druge jednadžbe slijedi [tex]x_1^2x_2y_1=-3y_1^2x_2y_1[/tex], odnosno [dtex](x_1^2+3y_1^2)x_2y_1=0.[/dtex]Prethodno je jednadžba u [tex]\mathbb{Z}[\sqrt 2][/tex]. Ali, [tex]\mathbb{Z}[\sqrt 2][/tex] je integralna domena pa ili je [tex]x_2y_1=0[/tex] (što povlači da je neki od [tex]x_2,y_1[/tex] jednak nuli, a to je suprotno pretpostavci) ili je [tex](x_1^2+3y_1^2)=0[/tex] što opet nije moguće. Prema tome, X je integralna domena.
____________________________________
3. zadatak. Neka je [tex]p(x)=a_0+a_1x+\cdots + a_nx^n \in\mathbb{Z}[x][/tex] polinom stupnja [tex]n\geq 0[/tex]. Onda je [tex]p(7x)=a_0+7a_1+\cdots 7^na_nx^n[/tex] polinom stupnja [tex]n\geq 0[/tex] s cjelobrojnim koeficijentima pa je [tex]p(7x)\in\mathbb{Z}[x][/tex], odnosno F je dobro definirano preslikavanje.
Neka je [tex]q(x)=b_0+b_1x+\cdots + b_mx^m \in\mathbb{Z}[x][/tex] polinom stupnja [tex]m\geq n[/tex] (bez smanjenja općenitosti). Neka je r(x)=p(x)+q(x). Onda je [dtex]\begin{eqnarray}F(r(x))=r(7x)=(a_0+b_0)+7(a_1+b_1)x+\cdots+7^n(a_n+b_n)x^n+7^{n+1}b_{n+1}x^{n+1}+\cdots 7^mb_mx^m=\\
a_0+7a_1x+\cdots + 7^na_nx^n+b_0+b_1x+\cdots + 7^nb_nx^n+7^{n+1}b_{n+1}x^{n+1}+\cdots 7^mb_mx^m=\\
p(7x)+q(7x)=F(p(x))+F(q(x)).\end{eqnarray}[/dtex] Dalje imamo [dtex]F(p(x)q(x))=F(\sum_{k=0}^{m+n}(\sum_{i+j=k}a_ib_j)x^k)=\sum_{k=0}^{m+n}F((\sum_{i+j=k}a_ib_j)x^k)=\sum_{k=0}^{m+n}(\sum_{i+j=k}a_ib_j)(7x)^k.[/dtex]
[dtex]F(p(x))F(q(x))=(\sum_{i=0}^n7^ia_ix^i)(\sum_{j=0}^m7^jb_jx^j)=\sum_{k=0}^{m+n}(\sum_{i+j=k}7^ia_i7^jb_j)x^k=\sum_{k=0}^{m+n}(\sum_{i+j=k}7^{i+j}a_ib_j)x^k=\sum_{k=0}^{m+n}(\sum_{i+j=k}a_ib_j)7^kx^k.[/dtex]
U jezgri tog preslikavanja nalazi se samo 0.
_________________
The Dude Abides
|
|
| [Vrh] |
|
GODIMENTI
Forumaš(ica)
Pridružen/a: 15. 02. 2011. (13:15:40)
Postovi: (9)16
|
|
| [Vrh] |
|
|















