| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
Gost
|
 Postano: 22:53 pon, 9. 8. 2004 Naslov: Rolleov teorem |
    |
|
Rolleov teorem:
Pretpostavke:
(i) f : I -> IR neprekidna na I = [a,b]
(ii) f(a) = f(b) = 0
(iii) f diferencijabilna u svakoj točki intervala <a,b>
Imam li pravo :
1.U prvoj pretpostavci mogli smo pretpostaviti i funkciju f definiranu na otvorenom intervalu ali kako nam u drugoj pretpostavci trebaju dvije točke domene sa konkretnim vrijednostima(nule) odcijepili bi suvišak toga otvorenog intervala(odnosno lijevo od točke a i desno od točke b) pa bi se razmatranje teorema opet svelo na promatranje segmenta.
Ili,smo uzeli segment kako bi imali funkciju neprekidnu na segmentu kakvu pretpostavlja BW-ov teorem koji nam treba u dokazu.
2.U trećoj pretpostavci mogli smo napisati 'f diferencijabilna u svakoj točki intervala [a,b] s time da u točki a je diferencijabilna zdesna,a u točki b slijeva' što nam se neda pisati s obzirom da za teorem nije potrebna diferencijabilnost u točkama a i b pa smo pretpostavili diferencijabilnost u <a,b>.
:?:
Pretpostavke:
(i) f : I → IR neprekidna na I = [a,b]
(ii) f(a) = f(b) = 0
(iii) f diferencijabilna u svakoj točki intervala <a,b>
Imam li pravo :
1.U prvoj pretpostavci mogli smo pretpostaviti i funkciju f definiranu na otvorenom intervalu ali kako nam u drugoj pretpostavci trebaju dvije točke domene sa konkretnim vrijednostima(nule) odcijepili bi suvišak toga otvorenog intervala(odnosno lijevo od točke a i desno od točke b) pa bi se razmatranje teorema opet svelo na promatranje segmenta.
Ili,smo uzeli segment kako bi imali funkciju neprekidnu na segmentu kakvu pretpostavlja BW-ov teorem koji nam treba u dokazu.
2.U trećoj pretpostavci mogli smo napisati 'f diferencijabilna u svakoj točki intervala [a,b] s time da u točki a je diferencijabilna zdesna,a u točki b slijeva' što nam se neda pisati s obzirom da za teorem nije potrebna diferencijabilnost u točkama a i b pa smo pretpostavili diferencijabilnost u <a,b>.
|
|
| [Vrh] |
|
ZELENIZUBNAPLANETIDO
SADE
Forumaš(ica)
Pridružen/a: 04. 03. 2004. (19:56:15)
Postovi: (54F)16
Lokacija: hm?
|
| Postano: 11:32 uto, 10. 8. 2004 Naslov: |
|
|
|
Ima par godina od onda, al... Derivabilnost sa lijeva i sa desna fje f u tockama a i b ti ne treba u dokazu teorema. Drugo, diferencijabilnost(derivabilnost) (kao i neprekidnost, al ona nam treba) je prirodnije promatrati na otvorenom skupu.
Sa druge strane, neprekidnost na segmentu je potrebna za primjenu BW teorema, pa je i ona uvijet.
ok?
Ima par godina od onda, al... Derivabilnost sa lijeva i sa desna fje f u tockama a i b ti ne treba u dokazu teorema. Drugo, diferencijabilnost(derivabilnost) (kao i neprekidnost, al ona nam treba) je prirodnije promatrati na otvorenom skupu.
Sa druge strane, neprekidnost na segmentu je potrebna za primjenu BW teorema, pa je i ona uvijet.
ok?
_________________ 
Pupoljak nije negiran. Rekao sam to i ponovit cu to jos jedanput. Pupoljak NIJE negirAn.
MADD
(Mothers Against Dirty Dialectics)
Based on a true story. NOT.
Ko ih sljivi, mi sviramo punk  |
|
| [Vrh] |
|
vsego
Site Admin
Pridružen/a: 06. 10. 2002. (22:07:09)
Postovi: (3562)16
Spol: 
Lokacija: /sbin/init
|
| Postano: 12:59 uto, 10. 8. 2004 Naslov: Re: Rolleov teorem |
|
|
[quote="Anonymous"]1.U prvoj pretpostavci mogli smo pretpostaviti i funkciju f definiranu na otvorenom intervalu ali kako nam u drugoj pretpostavci trebaju dvije točke domene sa konkretnim vrijednostima(nule) odcijepili bi suvišak toga otvorenog intervala(odnosno lijevo od točke a i desno od točke b) pa bi se razmatranje teorema opet svelo na promatranje segmenta.
Ili,smo uzeli segment kako bi imali funkciju neprekidnu na segmentu kakvu pretpostavlja BW-ov teorem koji nam treba u dokazu.[/quote]
Neprekidnost na segmentu ti svakako treba. 8) Jednostavan protuprimjer je fja: [latex]f(a)=f(b)=0, f(x)=1, x \ in <a,b>[/latex].
Ono sto smo mogli napraviti je napraviti ocito poopcenje:
(i') f : S -> IR neprekidna na I = [a,b], I podskup od S
[quote="Anonymous"]2.U trećoj pretpostavci mogli smo napisati 'f diferencijabilna u svakoj točki intervala [a,b] s time da u točki a je diferencijabilna zdesna,a u točki b slijeva' što nam se neda pisati s obzirom da za teorem nije potrebna diferencijabilnost u točkama a i b pa smo pretpostavili diferencijabilnost u <a,b>.[/quote]
Nije samo da nam se ne da pisati, nego je ovako preglednije, a i obuhvacamo veci broj funkcija na koje se teorem moze primijeniti. 8)
Inace, idealno je u teoremima postaviti samo [b]nuzne[/b] uvjete, tako da budu sto primjenjiviji. :D | Anonymous (napisa): | 1.U prvoj pretpostavci mogli smo pretpostaviti i funkciju f definiranu na otvorenom intervalu ali kako nam u drugoj pretpostavci trebaju dvije točke domene sa konkretnim vrijednostima(nule) odcijepili bi suvišak toga otvorenog intervala(odnosno lijevo od točke a i desno od točke b) pa bi se razmatranje teorema opet svelo na promatranje segmenta.
Ili,smo uzeli segment kako bi imali funkciju neprekidnu na segmentu kakvu pretpostavlja BW-ov teorem koji nam treba u dokazu. |
Neprekidnost na segmentu ti svakako treba.  Jednostavan protuprimjer je fja:  .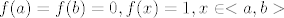
Ono sto smo mogli napraviti je napraviti ocito poopcenje:
(i') f : S → IR neprekidna na I = [a,b], I podskup od S
| Anonymous (napisa): | | 2.U trećoj pretpostavci mogli smo napisati 'f diferencijabilna u svakoj točki intervala [a,b] s time da u točki a je diferencijabilna zdesna,a u točki b slijeva' što nam se neda pisati s obzirom da za teorem nije potrebna diferencijabilnost u točkama a i b pa smo pretpostavili diferencijabilnost u <a,b>. |
Nije samo da nam se ne da pisati, nego je ovako preglednije, a i obuhvacamo veci broj funkcija na koje se teorem moze primijeniti.
Inace, idealno je u teoremima postaviti samo nuzne uvjete, tako da budu sto primjenjiviji. 
_________________ U pravilu ignoriram pitanja u krivim topicima i kodove koji nisu u [code]...[/code] blokovima.
Takodjer, OBJASNITE sto vas muci! "Sto mi je krivo?", bez opisa u cemu je problem, rijetko ce zadobiti moju paznju.  |
|
| [Vrh] |
|
Gost
|
| Postano: 15:03 uto, 10. 8. 2004 Naslov: |
|
|
[quote]Neprekidnost na segmentu ti svakako treba. [/quote]
Ma znam da bez neprekidnost niš'. :D
Ma nenamjerno sam falio u pretpostavci,mislio sam reći da možemo pretpostaviti funkciju NEPREKIDNU definiranu na otvorenu intervalu,hoću reći nije nužan baš zatvoreni interval kao domena funkcije.
[quote]Jednostavan protuprimjer je fja: .
f(a)=f(b)=0,f(x)=1,x@<a,b>
[/quote]
Protuprimjer da teorem može vrijediti i za prekidnu funkciju na segmentu jeli tako ?
[quote]Ono sto smo mogli napraviti je napraviti ocito poopcenje:
(i') f : S -> IR neprekidna na I = [a,b], I podskup od S
[/quote]
E vidiš to sam htio reći sa ovime :
1.U prvoj pretpostavci mogli smo pretpostaviti i funkciju f definiranu na otvorenom intervalu[color=green](neprekidnu)[/color] ali kako nam u drugoj pretpostavci trebaju dvije točke domene sa konkretnim vrijednostima(nule) odcijepili bi suvišak toga otvorenog intervala(odnosno lijevo od točke a i desno od točke b) pa bi se razmatranje teorema opet svelo na promatranje segmenta.
Ili,smo uzeli segment kako bi imali funkciju neprekidnu na segmentu kakvu pretpostavlja BW-ov teorem koji nam treba u dokazu.
Ja bi ovako postavio pretpostavke teorema:
(i) f : I -> IR , I = <a,b> diferencijabilna na I
(ii) f(a) = f(b) = 0
Btw:
Piše:
funkcija f : I -> IR je neprekidna na segmentu I = [a,b]
Nije li to neprecizno napisano ?
Nebi li trebalo pisati ovako:
Funkcija f je neprekidna u svim točkama domene s time da je u točki a neprekidna zdesna,a u točki b neprekidna slijeva. | Citat: | | Neprekidnost na segmentu ti svakako treba. |
Ma znam da bez neprekidnost niš'.
Ma nenamjerno sam falio u pretpostavci,mislio sam reći da možemo pretpostaviti funkciju NEPREKIDNU definiranu na otvorenu intervalu,hoću reći nije nužan baš zatvoreni interval kao domena funkcije.
| Citat: | Jednostavan protuprimjer je fja: .
f(a)=f(b)=0,f(x)=1,x@<a,b>
|
Protuprimjer da teorem može vrijediti i za prekidnu funkciju na segmentu jeli tako ?
| Citat: | Ono sto smo mogli napraviti je napraviti ocito poopcenje:
(i') f : S → IR neprekidna na I = [a,b], I podskup od S
|
E vidiš to sam htio reći sa ovime :
1.U prvoj pretpostavci mogli smo pretpostaviti i funkciju f definiranu na otvorenom intervalu(neprekidnu) ali kako nam u drugoj pretpostavci trebaju dvije točke domene sa konkretnim vrijednostima(nule) odcijepili bi suvišak toga otvorenog intervala(odnosno lijevo od točke a i desno od točke b) pa bi se razmatranje teorema opet svelo na promatranje segmenta.
Ili,smo uzeli segment kako bi imali funkciju neprekidnu na segmentu kakvu pretpostavlja BW-ov teorem koji nam treba u dokazu.
Ja bi ovako postavio pretpostavke teorema:
(i) f : I → IR , I = <a,b> diferencijabilna na I
(ii) f(a) = f(b) = 0
Btw:
Piše:
funkcija f : I → IR je neprekidna na segmentu I = [a,b]
Nije li to neprecizno napisano ?
Nebi li trebalo pisati ovako:
Funkcija f je neprekidna u svim točkama domene s time da je u točki a neprekidna zdesna,a u točki b neprekidna slijeva.
|
|
| [Vrh] |
|
mdoko
Forumaš(ica)
Pridružen/a: 30. 11. 2002. (22:17:12)
Postovi: (71A)16
Spol: 
Lokacija: Heriot-Watt University, Edinburgh
|
| Postano: 15:25 uto, 10. 8. 2004 Naslov: |
|
|
[quote][quote]
Jednostavan protuprimjer je fja: .
f(a)=f(b)=0,f(x)=1,x@<a,b>
[/quote]
Protuprimjer da teorem može vrijediti i za prekidnu funkciju na segmentu jeli tako ?
[/quote]
Pretpostavljam da je vsego zelio dati primjer funkcije koja ce zadovoljavati sve uvjete teorema osim neprekidnosti na [a,b], a teorem za nju ne bi vrijedio. To nije gore navedena funkcija nego: f(a)=f(b)=0,f(x)=x,x@<a,b>
sada se vidi da je f'(x)=1 za svaki x@<a,b>
[quote]Ja bi ovako postavio pretpostavke teorema:
(i) f : I -> IR , I = <a,b> diferencijabilna na I
(ii) f(a) = f(b) = 0 [/quote]
Kako? :shock:
Ako je domena funkcije f skup <a,b> kako onda uopce mozemo govoriti o f(a) i f(b), kaka a i b nisu u domeni funkcije? :roll:
[quote] Nebi li trebalo pisati ovako:
Funkcija f je neprekidna u svim točkama domene s time da je u točki a neprekidna zdesna,a u točki b neprekidna slijeva.[/quote]
Kada se govori o neprekidnosti na segmentu misli se upravo na to, odnosno definiramo da je neka funkcija neprekidna na segmentu [a,b], ako je neprekidna na intevalu <a,b> i u a neprekidna zdesna i u b neprekidnma s lijeva. :wink: | Citat: | | Citat: |
Jednostavan protuprimjer je fja: .
f(a)=f(b)=0,f(x)=1,x@<a,b>
|
Protuprimjer da teorem može vrijediti i za prekidnu funkciju na segmentu jeli tako ?
|
Pretpostavljam da je vsego zelio dati primjer funkcije koja ce zadovoljavati sve uvjete teorema osim neprekidnosti na [a,b], a teorem za nju ne bi vrijedio. To nije gore navedena funkcija nego: f(a)=f(b)=0,f(x)=x,x@<a,b>
sada se vidi da je f'(x)=1 za svaki x@<a,b>
| Citat: | Ja bi ovako postavio pretpostavke teorema:
(i) f : I → IR , I = <a,b> diferencijabilna na I
(ii) f(a) = f(b) = 0 |
Kako? 
Ako je domena funkcije f skup <a,b> kako onda uopce mozemo govoriti o f(a) i f(b), kaka a i b nisu u domeni funkcije? 
| Citat: | Nebi li trebalo pisati ovako:
Funkcija f je neprekidna u svim točkama domene s time da je u točki a neprekidna zdesna,a u točki b neprekidna slijeva. |
Kada se govori o neprekidnosti na segmentu misli se upravo na to, odnosno definiramo da je neka funkcija neprekidna na segmentu [a,b], ako je neprekidna na intevalu <a,b> i u a neprekidna zdesna i u b neprekidnma s lijeva.
_________________
Extraordinary claims require extraordinary evidence. – Carl Sagan
|
|
| [Vrh] |
|
Gost
|
| Postano: 16:12 uto, 10. 8. 2004 Naslov: |
|
|
[quote]Kako?
Ako je domena funkcije f skup <a,b> kako onda uopce mozemo govoriti o f(a) i f(b), kaka a i b nisu u domeni funkcije?
[/quote]
tipfeler pardon(mogao si i ovdje pretpostaviti što sam zapravo mislio;))
Dakle sve isto samo funkcijske vrijednosti preslikavaju točke c,d@I u nulu.
Jeli tako da je moguće imati isti zaključak teorema uz ovakve pretpostavke ?
[quote]Kada se govori o neprekidnosti na segmentu misli se upravo na to, odnosno definiramo da je neka funkcija neprekidna na segmentu [a,b], ako je neprekidna na intevalu <a,b> i u a neprekidna zdesna i u b neprekidnma s lijeva. [/quote]
Hvala,dakle u pitanju je lijenost pisanja. ;) | Citat: | Kako?
Ako je domena funkcije f skup <a,b> kako onda uopce mozemo govoriti o f(a) i f(b), kaka a i b nisu u domeni funkcije?
|
tipfeler pardon(mogao si i ovdje pretpostaviti što sam zapravo mislio;))
Dakle sve isto samo funkcijske vrijednosti preslikavaju točke c,d@I u nulu.
Jeli tako da je moguće imati isti zaključak teorema uz ovakve pretpostavke ?
| Citat: | | Kada se govori o neprekidnosti na segmentu misli se upravo na to, odnosno definiramo da je neka funkcija neprekidna na segmentu [a,b], ako je neprekidna na intevalu <a,b> i u a neprekidna zdesna i u b neprekidnma s lijeva. |
Hvala,dakle u pitanju je lijenost pisanja.
|
|
| [Vrh] |
|
vsego
Site Admin
Pridružen/a: 06. 10. 2002. (22:07:09)
Postovi: (3562)16
Spol:
Lokacija: /sbin/init
|
| Postano: 16:20 uto, 10. 8. 2004 Naslov: |
|
|
[quote="mdoko"][quote][quote]Jednostavan protuprimjer je fja: .
f(a)=f(b)=0,f(x)=1,x@<a,b>[/quote]
Protuprimjer da teorem može vrijediti i za prekidnu funkciju na segmentu jeli tako ?[/quote]
Pretpostavljam da je vsego zelio dati primjer funkcije koja ce zadovoljavati sve uvjete teorema osim neprekidnosti na [a,b], a teorem za nju ne bi vrijedio. To nije gore navedena funkcija nego: f(a)=f(b)=0,f(x)=x,x@<a,b>
sada se vidi da je f'(x)=1 za svaki x@<a,b>[/quote]
Hmda... :-s Tipfeller. :oops:
[quote="anonymous"]Hvala,dakle u pitanju je lijenost pisanja. ;)[/quote]
Ne kuzim... :-s Kakva lijenost?! :o | mdoko (napisa): | | Citat: | | Citat: | Jednostavan protuprimjer je fja: .
f(a)=f(b)=0,f(x)=1,x@<a,b> |
Protuprimjer da teorem može vrijediti i za prekidnu funkciju na segmentu jeli tako ? |
Pretpostavljam da je vsego zelio dati primjer funkcije koja ce zadovoljavati sve uvjete teorema osim neprekidnosti na [a,b], a teorem za nju ne bi vrijedio. To nije gore navedena funkcija nego: f(a)=f(b)=0,f(x)=x,x@<a,b>
sada se vidi da je f'(x)=1 za svaki x@<a,b> |
Hmda...  Tipfeller. 
| anonymous (napisa): | | Hvala,dakle u pitanju je lijenost pisanja. |
Ne kuzim... Kakva lijenost?! 
_________________ U pravilu ignoriram pitanja u krivim topicima i kodove koji nisu u [code]...[/code] blokovima.
Takodjer, OBJASNITE sto vas muci! "Sto mi je krivo?", bez opisa u cemu je problem, rijetko ce zadobiti moju paznju. |
|
| [Vrh] |
|
Gost
|
| Postano: 20:03 uto, 10. 8. 2004 Naslov: |
|
|
[quote]anonymous (napisa):
Hvala,dakle u pitanju je lijenost pisanja.
Ne kuzim... Kakva lijenost?!
[/quote]
Ma mislio sam na ovo:
Kažemo funkcija je neprekidna na segmentu [a,b] i pritom mislimo da je neprekidna na <a,b> te neprekidna zdesna u a i slijeva u b,dakle _nemoramo pisati_(na štetu preciznosti):
funkcija je neprekidna na segmentu s time(poradi preciznosti) da je u točki a zdesna,a u točki b slijeva.
Dakle ništa vrijedno velike zbunjenosti. :D :wink: | Citat: | anonymous (napisa):
Hvala,dakle u pitanju je lijenost pisanja.
Ne kuzim... Kakva lijenost?!
|
Ma mislio sam na ovo:
Kažemo funkcija je neprekidna na segmentu [a,b] i pritom mislimo da je neprekidna na <a,b> te neprekidna zdesna u a i slijeva u b,dakle _nemoramo pisati_(na štetu preciznosti):
funkcija je neprekidna na segmentu s time(poradi preciznosti) da je u točki a zdesna,a u točki b slijeva.
Dakle ništa vrijedno velike zbunjenosti.
|
|
| [Vrh] |
|
vsego
Site Admin
Pridružen/a: 06. 10. 2002. (22:07:09)
Postovi: (3562)16
Spol:
Lokacija: /sbin/init
|
| Postano: 20:27 uto, 10. 8. 2004 Naslov: |
|
|
[quote="Anonymous"]Ma mislio sam na ovo:
Kažemo funkcija je neprekidna na segmentu [a,b] i pritom mislimo da je neprekidna na <a,b> te neprekidna zdesna u a i slijeva u b,dakle _nemoramo pisati_(na štetu preciznosti):
funkcija je neprekidna na segmentu s time(poradi preciznosti) da je u točki a zdesna,a u točki b slijeva.[/quote]
Ali to nije ni lijenost ni "[i]na stetu preciznosti[/i]". :shock: To je [b]definicija[/b] neprekidnosti na segmentu! :prodike:
Kao da kazes da je "[i]prost (broj)[/i]" lijenost jer nam se ne da reci "[i]prirodan broj veci od 1 koji je djeljiv samo s 1 i sa samim sobom[/i]". :g: | Anonymous (napisa): | Ma mislio sam na ovo:
Kažemo funkcija je neprekidna na segmentu [a,b] i pritom mislimo da je neprekidna na <a,b> te neprekidna zdesna u a i slijeva u b,dakle _nemoramo pisati_(na štetu preciznosti):
funkcija je neprekidna na segmentu s time(poradi preciznosti) da je u točki a zdesna,a u točki b slijeva. |
Ali to nije ni lijenost ni "na stetu preciznosti". To je definicija neprekidnosti na segmentu!
Kao da kazes da je "prost (broj)" lijenost jer nam se ne da reci "prirodan broj veci od 1 koji je djeljiv samo s 1 i sa samim sobom". 
_________________ U pravilu ignoriram pitanja u krivim topicima i kodove koji nisu u [code]...[/code] blokovima.
Takodjer, OBJASNITE sto vas muci! "Sto mi je krivo?", bez opisa u cemu je problem, rijetko ce zadobiti moju paznju. |
|
| [Vrh] |
|
Gost
|
| Postano: 20:38 uto, 10. 8. 2004 Naslov: |
|
|
[quote="vsego"][quote="Anonymous"]Ma mislio sam na ovo:
Kažemo funkcija je neprekidna na segmentu [a,b] i pritom mislimo da je neprekidna na <a,b> te neprekidna zdesna u a i slijeva u b,dakle _nemoramo pisati_(na štetu preciznosti):
funkcija je neprekidna na segmentu s time(poradi preciznosti) da je u točki a zdesna,a u točki b slijeva.[/quote]
Ali to nije ni lijenost ni "[i]na stetu preciznosti[/i]". :shock: To je [b]definicija[/b] neprekidnosti na segmentu! :prodike:
Kao da kazes da je "[i]prost (broj)[/i]" lijenost jer nam se ne da reci "[i]prirodan broj veci od 1 koji je djeljiv samo s 1 i sa samim sobom[/i]". :g:[/quote]
Aha!
e onda kolega me imate u šaci i ispričavam se što sam mislio da niste shvatili što sam ja mislio,u krajnjoj liniji sam pomislio da ste velikom brzinom(munje) prošli kroz post pa niste primjetili.
:n00b: me! | vsego (napisa): | | Anonymous (napisa): | Ma mislio sam na ovo:
Kažemo funkcija je neprekidna na segmentu [a,b] i pritom mislimo da je neprekidna na <a,b> te neprekidna zdesna u a i slijeva u b,dakle _nemoramo pisati_(na štetu preciznosti):
funkcija je neprekidna na segmentu s time(poradi preciznosti) da je u točki a zdesna,a u točki b slijeva. |
Ali to nije ni lijenost ni "na stetu preciznosti". To je definicija neprekidnosti na segmentu!
Kao da kazes da je "prost (broj)" lijenost jer nam se ne da reci "prirodan broj veci od 1 koji je djeljiv samo s 1 i sa samim sobom". |
Aha!
e onda kolega me imate u šaci i ispričavam se što sam mislio da niste shvatili što sam ja mislio,u krajnjoj liniji sam pomislio da ste velikom brzinom(munje) prošli kroz post pa niste primjetili.
 me!
|
|
| [Vrh] |
|
ZELENIZUBNAPLANETIDO
SADE
Forumaš(ica)
Pridružen/a: 04. 03. 2004. (19:56:15)
Postovi: (54F)16
Lokacija: hm?
|
| Postano: 21:00 uto, 10. 8. 2004 Naslov: |
|
|
[quote="Anonymous"]Ma mislio sam na ovo:
Kažemo funkcija je neprekidna na segmentu [a,b] i pritom mislimo da je neprekidna na <a,b> te neprekidna zdesna u a i slijeva u b,dakle _nemoramo pisati_(na štetu preciznosti):
funkcija je neprekidna na segmentu s time(poradi preciznosti) da je u točki a zdesna,a u točki b slijeva.[/quote]
[quote="vsego"]Ali to nije ni lijenost ni "[i]na stetu preciznosti[/i]". :shock: To je [b]definicija[/b] neprekidnosti na segmentu! :prodike:[/quote]
Ako se ne varam, za potrebe BW tm (a i opcenito za prosirivanje teorije sa intervala na segmente) se koristi slijedeca definicija segmenta:
[latex][a,b] := \ bigcap_{\ overline{a}<a~ i ~\ overline{b}>b} {<\ overline{a},\ overline{b}>}[/latex]
Koncepti lijeve i desne neprekidnosti su tu u potpunosti nepotrebni.
btw: zna netko kako u gornjem tex-u natjerati nejednakosti da budu u razlicitim redovima? i da nejednakosti pisu _ispod_ \ bigcapa? | Anonymous (napisa): | Ma mislio sam na ovo:
Kažemo funkcija je neprekidna na segmentu [a,b] i pritom mislimo da je neprekidna na <a,b> te neprekidna zdesna u a i slijeva u b,dakle _nemoramo pisati_(na štetu preciznosti):
funkcija je neprekidna na segmentu s time(poradi preciznosti) da je u točki a zdesna,a u točki b slijeva. |
| vsego (napisa): | | Ali to nije ni lijenost ni "na stetu preciznosti". To je definicija neprekidnosti na segmentu! |
Ako se ne varam, za potrebe BW tm (a i opcenito za prosirivanje teorije sa intervala na segmente) se koristi slijedeca definicija segmenta:
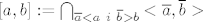
Koncepti lijeve i desne neprekidnosti su tu u potpunosti nepotrebni.
btw: zna netko kako u gornjem tex-u natjerati nejednakosti da budu u razlicitim redovima? i da nejednakosti pisu _ispod_ \bigcapa?
_________________
Pupoljak nije negiran. Rekao sam to i ponovit cu to jos jedanput. Pupoljak NIJE negirAn.
MADD
(Mothers Against Dirty Dialectics)
Based on a true story. NOT.
Ko ih sljivi, mi sviramo punk |
|
| [Vrh] |
|
Gost
|
| Postano: 13:05 sri, 11. 8. 2004 Naslov: |
|
|
što onda,vrijede li moje pretpostavke za Rolleov teorem ? :
(i) f : I -> IR , I = <a,b> diferencijabilna na I
(ii) f(c) = f(d) = 0 , c,d@I
Naravno,svjestan sam da možda zahtjevam više nego što mi treba. :wink:
Btw zeleni hvala na tvojoj vidno-šokirajućoj definiciji segmenta,ali ne hvala :D
(i) f : I -> IR , I = <a,b> diferencijabilna na I
(ii) f(c) = f(d) = 0 , c,d@I
Naravno,svjestan sam da možda zahtjevam više nego što mi treba.
Btw zeleni hvala na tvojoj vidno-šokirajućoj definiciji segmenta,ali ne hvala
|
|
| [Vrh] |
|
ZELENIZUBNAPLANETIDO
SADE
Forumaš(ica)
Pridružen/a: 04. 03. 2004. (19:56:15)
Postovi: (54F)16
Lokacija: hm?
|
| Postano: 15:22 sri, 11. 8. 2004 Naslov: |
|
|
[quote="Anonymous"]što onda,vrijede li moje pretpostavke za Rolleov teorem ? :
(i) f : I -> IR , I = <a,b> diferencijabilna na I
(ii) f(c) = f(d) = 0 , c,d@I[/quote]
Pa.. Ovakve pretpostavke te nece odvesti u kontradikciju, ali ce ti ujedno onemoguciti primjenu "tvog" :) teorema u nekim situacijama u kojima bi se "normalni" Rolleov teorem mogao primijeniti. Ili.. drugim rijecima trazis vise nego ti treba. :g:
[quote="Anonymous"]Naravno,svjestan sam da možda zahtjevam više nego što mi treba. :wink:[/quote]
Onda je sve u redu :g:
No pripazi, zasto ti je teze prihvatiti blago zaguljenu definiciju nego si znacajno "potkresati krila" i ograniciti primijenjivost propozicije? :-k
Ta definicija je 1-dimenzionalna verzija jedne od najelementarnijih definicija koje ces uciti na prvom predavanju analize 3 i koristiti do kraja skolovanja. Preporucio bih ti da se naviknes na nju.
[quote="Anonymous"]Btw zeleni hvala na tvojoj vidno-šokirajućoj definiciji segmenta,ali ne hvala :D[/quote]
Nemoj mene gledat :D Tako ste ga _VI_ definirali na predavanjima :g: | Anonymous (napisa): | što onda,vrijede li moje pretpostavke za Rolleov teorem ? :
(i) f : I → IR , I = <a,b> diferencijabilna na I
(ii) f(c) = f(d) = 0 , c,d@I |
Pa.. Ovakve pretpostavke te nece odvesti u kontradikciju, ali ce ti ujedno onemoguciti primjenu "tvog"  teorema u nekim situacijama u kojima bi se "normalni" Rolleov teorem mogao primijeniti. Ili.. drugim rijecima trazis vise nego ti treba.
| Anonymous (napisa): | | Naravno,svjestan sam da možda zahtjevam više nego što mi treba. |
Onda je sve u redu
No pripazi, zasto ti je teze prihvatiti blago zaguljenu definiciju nego si znacajno "potkresati krila" i ograniciti primijenjivost propozicije? 
Ta definicija je 1-dimenzionalna verzija jedne od najelementarnijih definicija koje ces uciti na prvom predavanju analize 3 i koristiti do kraja skolovanja. Preporucio bih ti da se naviknes na nju.
| Anonymous (napisa): | | Btw zeleni hvala na tvojoj vidno-šokirajućoj definiciji segmenta,ali ne hvala |
Nemoj mene gledat Tako ste ga _VI_ definirali na predavanjima
_________________
Pupoljak nije negiran. Rekao sam to i ponovit cu to jos jedanput. Pupoljak NIJE negirAn.
MADD
(Mothers Against Dirty Dialectics)
Based on a true story. NOT.
Ko ih sljivi, mi sviramo punk |
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
ZELENIZUBNAPLANETIDO
SADE
Forumaš(ica)
Pridružen/a: 04. 03. 2004. (19:56:15)
Postovi: (54F)16
Lokacija: hm?
|
| Postano: 16:54 sri, 11. 8. 2004 Naslov: |
|
|
[quote="Anonymous"]Nemoj TI mene gledat! :crazy: :g:
Da sam ja definirao segment stvar bi izgledala puno ljepše i bude izgledala ljepše čim se sjetim prikladnije definicije. :grebgreb: :^o[/quote]
:bow: :pray: 8)
Gledaj to ovako:
imas nesto definirano na otvorenom skupu sto zelis iskoristiti na segmentu. Drugim rijecima, moras uzeti interval takav da ti segment cijeli stane u njega a da ne bude veci (od segmenta), tj. da mu ne bude strogi nadskup.
Blagi mission impossible, ali izvediv, i budi siguran, kako god ga izveo, nece izgledati jednostavno i ona definicija je vise-manje ono sto trazis :|
Al ne skodi malo konstruktivnog razbijanja glave pa te ostavljam u tvom poslu ;)
btw: mozda ovako :)
[latex][a,b] := \ bigcap_{<a,b> \ subset <\ overline{a},\ overline{b}>} {<\ overline{a},\ overline{b}>}[/latex] | Anonymous (napisa): | Nemoj TI mene gledat! 
Da sam ja definirao segment stvar bi izgledala puno ljepše i bude izgledala ljepše čim se sjetim prikladnije definicije.   |
 
Gledaj to ovako:
imas nesto definirano na otvorenom skupu sto zelis iskoristiti na segmentu. Drugim rijecima, moras uzeti interval takav da ti segment cijeli stane u njega a da ne bude veci (od segmenta), tj. da mu ne bude strogi nadskup.
Blagi mission impossible, ali izvediv, i budi siguran, kako god ga izveo, nece izgledati jednostavno i ona definicija je vise-manje ono sto trazis 
Al ne skodi malo konstruktivnog razbijanja glave pa te ostavljam u tvom poslu
btw: mozda ovako
_________________
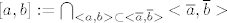
Pupoljak nije negiran. Rekao sam to i ponovit cu to jos jedanput. Pupoljak NIJE negirAn.
MADD
(Mothers Against Dirty Dialectics)
Based on a true story. NOT.
Ko ih sljivi, mi sviramo punk |
|
| [Vrh] |
|
veky
Forumaš(ica)
Pridružen/a: 09. 12. 2002. (19:59:43)
Postovi: (5B0)16
Lokacija: negdje daleko...
|
| Postano: 10:50 pet, 27. 8. 2004 Naslov: |
|
|
[quote="ZELENIZUBNAPLANETIDOSADE"]
Ako se ne varam, za potrebe BW tm (a i opcenito za prosirivanje teorije sa intervala na segmente) se koristi slijedeca definicija segmenta:
[latex][a,b] := \ bigcap_{\ overline{a}<a~ i ~\ overline{b}>b} {<\ overline{a},\ overline{b}>}[/latex][/quote]
Mislim da je "definicija" ipak malo pregruba riječ. Ja ne bih htio tako definirati segment. (U uređenim skupovima koji nisu uređajno potpuni, mogle bi se dogoditi čudne stvari.) :-o
"karakterizacija", IMO.
[quote]btw: zna netko kako u gornjem tex-u natjerati nejednakosti da budu u razlicitim redovima? i da nejednakosti pisu _ispod_ \ bigcapa?[/quote]
Ne znam (ovdje... inače znam bar ovo drugo: ), ali znam nešto drugo: za otvorene intervale i trebaju \ langle i \ rangle , _ne_ < i > . Prvo sam zbunjeno dvije minute buljio što ti znači interval <a i b> ... :-o ;-) | ZELENIZUBNAPLANETIDOSADE (napisa): |
Ako se ne varam, za potrebe BW tm (a i opcenito za prosirivanje teorije sa intervala na segmente) se koristi slijedeca definicija segmenta:
|
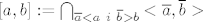Mislim da je "definicija" ipak malo pregruba riječ. Ja ne bih htio tako definirati segment. (U uređenim skupovima koji nisu uređajno potpuni, mogle bi se dogoditi čudne stvari.)
"karakterizacija", IMO.
| Citat: | | btw: zna netko kako u gornjem tex-u natjerati nejednakosti da budu u razlicitim redovima? i da nejednakosti pisu _ispod_ \bigcapa? |
Ne znam (ovdje... inače znam bar ovo drugo: ), ali znam nešto drugo: za otvorene intervale i trebaju \langle i \rangle , _ne_ < i > . Prvo sam zbunjeno dvije minute buljio što ti znači interval <a i b> ...
|
|
| [Vrh] |
|
ZELENIZUBNAPLANETIDO
SADE
Forumaš(ica)
Pridružen/a: 04. 03. 2004. (19:56:15)
Postovi: (54F)16
Lokacija: hm?
|
| Postano: 15:07 pet, 27. 8. 2004 Naslov: |
|
|
[quote="veky"]Ne znam (ovdje... inače znam bar ovo drugo: ), ali znam nešto drugo: za otvorene intervale i trebaju \ langle i \ rangle , _ne_ < i > . Prvo sam zbunjeno dvije minute buljio što ti znači interval <a i b> ... :-o ;-)[/quote]
ah :) a kako bi to islo u "true latexu" ? :)
:valovi: | veky (napisa): | | Ne znam (ovdje... inače znam bar ovo drugo: ), ali znam nešto drugo: za otvorene intervale i trebaju \langle i \rangle , _ne_ < i > . Prvo sam zbunjeno dvije minute buljio što ti znači interval <a i b> ... |
ah a kako bi to islo u "true latexu" ?
_________________
Pupoljak nije negiran. Rekao sam to i ponovit cu to jos jedanput. Pupoljak NIJE negirAn.
MADD
(Mothers Against Dirty Dialectics)
Based on a true story. NOT.
Ko ih sljivi, mi sviramo punk |
|
| [Vrh] |
|
|
