| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
pedro
Forumaš(ica)

Pridružen/a: 21. 10. 2010. (14:08:21)
Postovi: (19B)16
|
 Postano: 17:24 sub, 3. 11. 2012 Naslov: Postano: 17:24 sub, 3. 11. 2012 Naslov: |
    |
|
|
[quote="simon11"]
[quote]je li moguće za K ovako pokazati ograničenost:[/quote]
Vech je kolega pokazao da taj skup nije ograničen tako shto je prept.suprotno i doshao do kontradikcije :D
[/quote]
lapsus, mislila sam možemo li tako pokazati da K nije ograničen:
za svaki xw iz R postoji yz iz R za koje vrijedi xw = yz, iz čeg slijedi da nije ograničen?
[size=9][color=#999999]Added after 4 minutes:[/color][/size]
[quote="simon11"][quote]je li to uredu? i ispričavam se na neurednom načinu zapisa [/quote]
Mislim da nije,jer si ovdje [quote]f(x,0) = 1/x * sinx -> konvergira k 1 kada x->0[/quote] uzela samo jednu jedinu restrikciju pa nisi mogla zakljuciti da to vrijedi,barem ne nuzno,cak:
[latex]f(x,y)=\frac{1}{x}sin\frac{x^3}{x^2+y^2}[/latex], promatram niz
[latex](\frac{1}{n},\frac{1}{n})\leadsto (0,0) [/latex] kada [latex]\ n \leadsto \infty[/latex]
i sada bash kao sto si napisala
[latex]f(x,y)=\frac{sin\frac{x^3}{x^2+y^2}}{\frac{x^3}{x^2+y^2}}\cdot \frac{x^2}{x^2+y^2}[/latex]
pa je, [latex]\lim_{n \to \infty}f(\frac{1}{n},\frac{1}{n})=\frac{1}{2}[/latex]
Dok za neki drugi niz,npr. [latex](\frac{1}{n},0)\leadsto (0,0) [/latex] kada [latex]\ n \leadsto \infty[/latex] vrijedi :
[latex]\lim_{n \to \infty}f(\frac{1}{n},0)=1[/latex].Dakle u tochki [latex](0,0)[/latex] uoce nema limesa.
Sada da bismo pokazali da u tochki [latex](0,y)\ y\neq 0[/latex] postoji limes potrebno je dokazati prema Heinovoj karakter.da SVI nizovi koji konvergiraju prema [latex](0,y)\ y\neq 0[/latex] da im niz slika kovergiraju prema [latex]f(0,y)\ y\neq 0[/latex].zato,uzimam prozvoljan niz [latex](x_n,y_n) \leadsto (0,y)\ y\neq 0[/latex] i tada je :
[latex]\lim_{n \to \infty}f(x_n,y_n)=0[/latex].
Dakle f-ju je moguce dodefinirati:
[latex]f(x,y)= \left\{ \begin{array}{rcl}
f(x,y)=\frac{1}{x}sin\frac{x^3}{x^2+y^2} & \mbox{za} & (x,y) \in D_f \right \\
0 & \mbox{za} & (x,y)=(0,y)\ y\neq 0 \right \\
\end{array}\right.[/latex]
[/quote]
a kaj je s uvjetom (0,y), kada je y = 0?
| simon11 (napisa): |
| Citat: | | je li moguće za K ovako pokazati ograničenost: |
Vech je kolega pokazao da taj skup nije ograničen tako shto je prept.suprotno i doshao do kontradikcije 
|
lapsus, mislila sam možemo li tako pokazati da K nije ograničen:
za svaki xw iz R postoji yz iz R za koje vrijedi xw = yz, iz čeg slijedi da nije ograničen?
Added after 4 minutes:
| simon11 (napisa): | | Citat: | | je li to uredu? i ispričavam se na neurednom načinu zapisa |
Mislim da nije,jer si ovdje | Citat: | | f(x,0) = 1/x * sinx → konvergira k 1 kada x→0 |
uzela samo jednu jedinu restrikciju pa nisi mogla zakljuciti da to vrijedi,barem ne nuzno,cak:
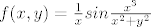 , promatram niz , promatram niz
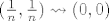 kada kada 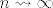
i sada bash kao sto si napisala
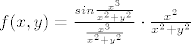
pa je, 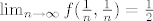
Dok za neki drugi niz,npr. 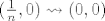 kada kada 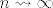 vrijedi : vrijedi :
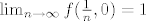 .Dakle u tochki .Dakle u tochki 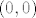 uoce nema limesa. uoce nema limesa.
Sada da bismo pokazali da u tochki 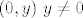 postoji limes potrebno je dokazati prema Heinovoj karakter.da SVI nizovi koji konvergiraju prema postoji limes potrebno je dokazati prema Heinovoj karakter.da SVI nizovi koji konvergiraju prema 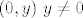 da im niz slika kovergiraju prema da im niz slika kovergiraju prema 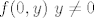 .zato,uzimam prozvoljan niz .zato,uzimam prozvoljan niz 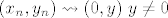 i tada je : i tada je :
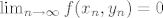 . .
Dakle f-ju je moguce dodefinirati:
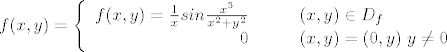
|
a kaj je s uvjetom (0,y), kada je y = 0?
|
|
| [Vrh] |
|
Zenon
Forumaš(ica)


Pridružen/a: 09. 09. 2011. (19:14:43)
Postovi: (2B1)16
Sarma: -
Lokacija: [tex]\pm\infty[/tex]
|
|
| [Vrh] |
|
simon11
Forumaš(ica)


Pridružen/a: 01. 10. 2011. (21:02:52)
Postovi: (7C)16
Spol: 
Lokacija: FunkyTown
|
|
| [Vrh] |
|
Ryssa
Forumaš(ica)


Pridružen/a: 18. 12. 2011. (00:10:28)
Postovi: (57)16
|
|
| [Vrh] |
|
pedro
Forumaš(ica)

Pridružen/a: 21. 10. 2010. (14:08:21)
Postovi: (19B)16
|
 Postano: 18:09 sub, 3. 11. 2012 Naslov: Postano: 18:09 sub, 3. 11. 2012 Naslov: |
    |
|
|
[quote="simon11"]Pa,tada sam promatrao dva niza koji teze u u tocku [latex](0,0)[/latex] i dobio sam dva razlicita limesa,a limes ako postoji mora biti jedinstven.[/quote]
pa da, al što to onda znači? očito se funkcija ne može dodefinirati u točki (0,0), što znači da se ne može dodefinirati na gomilištu domene, a gomilište je cijeli R^2 zar ne?
[size=9][color=#999999]Added after 1 minutes:[/color][/size]
[quote="Zenon"][quote="pedro"]a kaj je s uvjetom (0,y), kada je y = 0?[/quote]
A u tom slučaju... A jednostavno ponovno pročitaj kolegin post, jer je i to riješio.[/quote]
ma nemoj??? -.-
| simon11 (napisa): | Pa,tada sam promatrao dva niza koji teze u u tocku 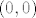 i dobio sam dva razlicita limesa,a limes ako postoji mora biti jedinstven. i dobio sam dva razlicita limesa,a limes ako postoji mora biti jedinstven. |
pa da, al što to onda znači? očito se funkcija ne može dodefinirati u točki (0,0), što znači da se ne može dodefinirati na gomilištu domene, a gomilište je cijeli R^2 zar ne?
Added after 1 minutes:
| Zenon (napisa): | | pedro (napisa): | | a kaj je s uvjetom (0,y), kada je y = 0? |
A u tom slučaju... A jednostavno ponovno pročitaj kolegin post, jer je i to riješio. |
ma nemoj??? -.-
|
|
| [Vrh] |
|
Phoenix
Forumaš(ica)


Pridružen/a: 15. 05. 2010. (18:46:07)
Postovi: (164)16
Sarma: -
|
|
| [Vrh] |
|
grizly
Forumaš(ica)

Pridružen/a: 26. 01. 2011. (21:30:01)
Postovi: (27)16
Spol: 
|
 Postano: 18:34 sub, 3. 11. 2012 Naslov: Postano: 18:34 sub, 3. 11. 2012 Naslov: |
    |
|
|
[quote="pedro"][quote="grizly"]a) Zapravo bi trebalo objasniti ovo "vidimo da su neprekidne", radi se o zbroju i razlici projekcija, a projekcije su nepekidne.
b) Kako su norme ekvivalentne možemo dokazivati u kojoj hoćemo meni se norma 1 činila dosta zgodna. U definiciji uniformne neprekidnosti uzmimo delta jednak epsilon polovina (d = e/2). Sada za x i y takve da je d(x,y)<d imamo zapravo raspisano po komponentama |x1-y1|+|x2-y2|+|x3-y3|<d. Sada pogledamo što je d(f(x),f(y)) = |x1-x3-y1+y3| + |x1+x2-y1-y2| što je po nejednakosti trokuta manje ili jednako od |x1-y1| + |x3-y3| + |x1-y1| + |x2-y2| što je (pogledaj udaljenost od x i y) definitivno manje ili jednako 2d(x,y) < 2d = e. Dakle f je uniformno neprekidna.
d) pogledaj propoziciju 11.13. s predavanja, trebaš samo pomnožiti danim vektorom (jer su ti ga baš dali normiranog).
Joj sorry tek sad vidim, vektor samo transponiraj :) i onda je ok[/quote]
a) da, da to uvijek prokomentiram kak smo radili i na vježbama :) samo me ovo dokažite buni, radije da bi piše pokaži :)
b) znači ti si na ovom djelu
|x1-y1| + |x3-y3| + |x1-y1| + |x2-y2| <= 2d(x,y) < 2d = e namještavao da dobiješ sam e na kraju i onda se pokaže da je funckija uniformno nepr, to je ideja?
c) hmm, nije mi jasno zašto transponirano?
[size=9][color=#999999]Added after 12 minutes:[/color][/size]
dobila sam da je derivacija 0, tj dobila sam 2 x 1 matricu sa svim elementima jednakim 0 :!:[/quote]
A da, dokaži zvuči puno moćnije, što može i ne mora biti dobra stvar :D
Pa za sve te epsilon delta definicije je to ideja (uglavnom su dobro kad pišu zadatke pa je jako lako naći deltu), ali mislim da je to puno puta viđeno na analizi, jedino što sada prvi put traže od tebe da tražiš deltu.
Transponira se zbog definicije skalarnog produkta (a i kad nisi sigurna, namještaj da se martice/vektori slažu) XD
A nisam množila, ali zapravo ne vidim razlog da je nul-vektor zabranjen. Sad en stignem množiti to jer žurim na hitnu XD
| pedro (napisa): | | grizly (napisa): | a) Zapravo bi trebalo objasniti ovo "vidimo da su neprekidne", radi se o zbroju i razlici projekcija, a projekcije su nepekidne.
b) Kako su norme ekvivalentne možemo dokazivati u kojoj hoćemo meni se norma 1 činila dosta zgodna. U definiciji uniformne neprekidnosti uzmimo delta jednak epsilon polovina (d = e/2). Sada za x i y takve da je d(x,y)<d imamo zapravo raspisano po komponentama |x1-y1|+|x2-y2|+|x3-y3|<d. Sada pogledamo što je d(f(x),f(y)) = |x1-x3-y1+y3| + |x1+x2-y1-y2| što je po nejednakosti trokuta manje ili jednako od |x1-y1| + |x3-y3| + |x1-y1| + |x2-y2| što je (pogledaj udaljenost od x i y) definitivno manje ili jednako 2d(x,y) < 2d = e. Dakle f je uniformno neprekidna.
d) pogledaj propoziciju 11.13. s predavanja, trebaš samo pomnožiti danim vektorom (jer su ti ga baš dali normiranog).
Joj sorry tek sad vidim, vektor samo transponiraj  i onda je ok i onda je ok |
a) da, da to uvijek prokomentiram kak smo radili i na vježbama  samo me ovo dokažite buni, radije da bi piše pokaži samo me ovo dokažite buni, radije da bi piše pokaži 
b) znači ti si na ovom djelu
|x1-y1| + |x3-y3| + |x1-y1| + |x2-y2| ⇐ 2d(x,y) < 2d = e namještavao da dobiješ sam e na kraju i onda se pokaže da je funckija uniformno nepr, to je ideja?
c) hmm, nije mi jasno zašto transponirano?
Added after 12 minutes:
dobila sam da je derivacija 0, tj dobila sam 2 x 1 matricu sa svim elementima jednakim 0  |
A da, dokaži zvuči puno moćnije, što može i ne mora biti dobra stvar 
Pa za sve te epsilon delta definicije je to ideja (uglavnom su dobro kad pišu zadatke pa je jako lako naći deltu), ali mislim da je to puno puta viđeno na analizi, jedino što sada prvi put traže od tebe da tražiš deltu.
Transponira se zbog definicije skalarnog produkta (a i kad nisi sigurna, namještaj da se martice/vektori slažu) XD
A nisam množila, ali zapravo ne vidim razlog da je nul-vektor zabranjen. Sad en stignem množiti to jer žurim na hitnu XD
_________________ Nit' sam normalna nit' se s takvima družim
 |
|
| [Vrh] |
|
homoviator
Forumaš(ica)
Pridružen/a: 31. 01. 2011. (18:42:32)
Postovi: (3A)16
|
|
| [Vrh] |
|
Phoenix
Forumaš(ica)


Pridružen/a: 15. 05. 2010. (18:46:07)
Postovi: (164)16
Sarma: -
|
 Postano: 23:48 sub, 3. 11. 2012 Naslov: Postano: 23:48 sub, 3. 11. 2012 Naslov: |
    |
|
|
Tako je. :)
Jedino za d), niz [tex]f(x_n)[/tex] ne mora divergirati, ali konvergira prema nekom [tex]f(c)[/tex] zbog neprekidnosti. No, [tex]c \in A[/tex], pa je [tex]f(c) \in f(A)[/tex], dakle [tex]f(A)[/tex] sadrži sva svoja gomilišta.
(Ili malo bolje: pretpostavi suprotno, postoji gomilište skupa [tex]f(A)[/tex] koje nije element tog skupa. Tada... I kontradikcija!)
Tako je. 
Jedino za d), niz [tex]f(x_n)[/tex] ne mora divergirati, ali konvergira prema nekom [tex]f(c)[/tex] zbog neprekidnosti. No, [tex]c \in A[/tex], pa je [tex]f(c) \in f(A)[/tex], dakle [tex]f(A)[/tex] sadrži sva svoja gomilišta.
(Ili malo bolje: pretpostavi suprotno, postoji gomilište skupa [tex]f(A)[/tex] koje nije element tog skupa. Tada... I kontradikcija!)
|
|
| [Vrh] |
|
goranm
Forumaš(ica)


Pridružen/a: 12. 11. 2002. (20:09:12)
Postovi: (906)16
Spol: 
|
 Postano: 23:58 sub, 3. 11. 2012 Naslov: Postano: 23:58 sub, 3. 11. 2012 Naslov: |
    |
|
|
[quote="homoviator"]Pod c) baš zbog toga što je [latex]A \subseteq \mathbb R^n[/latex], a ne [latex]\subset [/latex] A ne mora nužno biti ograničen u smislu može biti baš jednak [latex]\mathbb R^n[/latex] ili griješim...[/quote]
Ne grijesis. Ako zelis strogi podskup, spomenuo si i sam u b), A je zatvoren akko je potpun. Odaberi onda bilo koji neomedjeni zatvoren skup u [tex]\mathbb{R}^n[/tex], npr. [tex]x\geq 0[/tex].
[quote]Pod d) Po Heinovoj krakterizaciji f(A) mora biti zatvoren(iz b) dijela dokazano da je A zatvoren ), inače bi postojao neki niz u A koji konvergira u npr. točku c iz A, a limes njegovih funkcijskih vrijednosti divergira pa bi to vodilo u kontradikciju... ili opet griješim?[/quote]
Ovdje grijesis. Ako za A uzmes [tex]\mathbb{R}[/tex], onda f(x)=arctanx ima sliku koja je otvoren, ali ne i zatvoren podskup realnih brojeva. Ako zelis pravi podskup, za [tex]A=\left<-\infty,0\right][/tex] i [tex]f(x)=e^x[/tex] slika ce biti [tex]\left<0,1\right][/tex].
Nevezano uz gradivo ovog kolegija, zahtjev da neprekidna funkcija salje zatvorene skupove u zatvorene je dosta jak. Takvo preslikavanje, ukoliko je surjektivno (a uvijek se moze natjerati do surjekcije tako da se ogranici kodomena) pripada klasi tzv. kvocijentnih preslikavanja koja su vrlo korisna u metrickim/topoloskim prostorima.
| homoviator (napisa): | Pod c) baš zbog toga što je 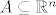 , a ne , a ne 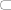 A ne mora nužno biti ograničen u smislu može biti baš jednak A ne mora nužno biti ograničen u smislu može biti baš jednak 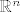 ili griješim... ili griješim... |
Ne grijesis. Ako zelis strogi podskup, spomenuo si i sam u b), A je zatvoren akko je potpun. Odaberi onda bilo koji neomedjeni zatvoren skup u [tex]\mathbb{R}^n[/tex], npr. [tex]x\geq 0[/tex].
| Citat: | | Pod d) Po Heinovoj krakterizaciji f(A) mora biti zatvoren(iz b) dijela dokazano da je A zatvoren ), inače bi postojao neki niz u A koji konvergira u npr. točku c iz A, a limes njegovih funkcijskih vrijednosti divergira pa bi to vodilo u kontradikciju... ili opet griješim? |
Ovdje grijesis. Ako za A uzmes [tex]\mathbb{R}[/tex], onda f(x)=arctanx ima sliku koja je otvoren, ali ne i zatvoren podskup realnih brojeva. Ako zelis pravi podskup, za [tex]A=\left←\infty,0\right][/tex] i [tex]f(x)=e^x[/tex] slika ce biti [tex]\left<0,1\right][/tex].
Nevezano uz gradivo ovog kolegija, zahtjev da neprekidna funkcija salje zatvorene skupove u zatvorene je dosta jak. Takvo preslikavanje, ukoliko je surjektivno (a uvijek se moze natjerati do surjekcije tako da se ogranici kodomena) pripada klasi tzv. kvocijentnih preslikavanja koja su vrlo korisna u metrickim/topoloskim prostorima.
_________________
The Dude Abides
Zadnja promjena: goranm; 4:41 ned, 4. 11. 2012; ukupno mijenjano 1 put.
|
|
| [Vrh] |
|
frutabella
Forumaš(ica)

Pridružen/a: 09. 10. 2010. (16:35:36)
Postovi: (24E)16
|
 Postano: 3:52 ned, 4. 11. 2012 Naslov: Postano: 3:52 ned, 4. 11. 2012 Naslov: |
    |
|
|
Ja sam ovaj 6.zad ovako rijesila:
a) Da, potpun je. Prema Tm 4.17 (skup je zatvoren akko svaki niz iz tog skupa konvergira u R^n i ima limes u A) zakljucujem da je A zatvoren. Zatim prema Prop 4.25, koja kaze, ako je A podskup od R^n zatvoren (akko) tada je potpun.
Zar definicija ne povlaci samo jednu stranu --->, potpun je ako svaki cauchyev niz konvergira u njemu, ali ne znamo da li vrijedi obrat.
b) Da, prema upravo gore navedenom Tm 4.17.
c) Da. Prema Tm 5.3. skup A je kompaktan akko svaki niz u A ima konvergentan podniz ciji je limes u A.
Buduci je Cauch.niz u A ogranicen (jer je svaki Cauc.niz ogranicen), prema teoremu o nizovima (koji kaze da svaki ogranicen niz ima konvergentan podniz) Cauch.niz ima konvergentan podniz u A, pa iz Tm 5.3. zakljucujemo da je niz kompaktan.
d) Da. Buduci je A kompaktan i f neprekidna, prema Tm 7.1., tada je f(A) kompaktan, a to znaci i zatvoren.
Da li su ovo dobri odgovori?
Ja sam ovaj 6.zad ovako rijesila:
a) Da, potpun je. Prema Tm 4.17 (skup je zatvoren akko svaki niz iz tog skupa konvergira u R^n i ima limes u A) zakljucujem da je A zatvoren. Zatim prema Prop 4.25, koja kaze, ako je A podskup od R^n zatvoren (akko) tada je potpun.
Zar definicija ne povlaci samo jednu stranu --->, potpun je ako svaki cauchyev niz konvergira u njemu, ali ne znamo da li vrijedi obrat.
b) Da, prema upravo gore navedenom Tm 4.17.
c) Da. Prema Tm 5.3. skup A je kompaktan akko svaki niz u A ima konvergentan podniz ciji je limes u A.
Buduci je Cauch.niz u A ogranicen (jer je svaki Cauc.niz ogranicen), prema teoremu o nizovima (koji kaze da svaki ogranicen niz ima konvergentan podniz) Cauch.niz ima konvergentan podniz u A, pa iz Tm 5.3. zakljucujemo da je niz kompaktan.
d) Da. Buduci je A kompaktan i f neprekidna, prema Tm 7.1., tada je f(A) kompaktan, a to znaci i zatvoren.
Da li su ovo dobri odgovori?
|
|
| [Vrh] |
|
goranm
Forumaš(ica)


Pridružen/a: 12. 11. 2002. (20:09:12)
Postovi: (906)16
Spol: 
|
 Postano: 4:21 ned, 4. 11. 2012 Naslov: Postano: 4:21 ned, 4. 11. 2012 Naslov: |
    |
|
|
[quote="frutabella"]Zar definicija ne povlaci samo jednu stranu --->, potpun je ako svaki cauchyev niz konvergira u njemu, ali ne znamo da li vrijedi obrat.[/quote]
Definicija nista ne povlaci. Definicija uvodi novi tremin, u ovom slucaju taj termin je potpun prostor. Kazemo da je prostor X potpun ako je svaki Cauchyev niz u X konvergentan u X. To je razlicito od "Ako je X potpun, onda je...". Prvo je definicija (rijec "kazemo" je kljucna), a drugo je izjava koja je istinita ili lazna.
[quote]c) Da. Prema Tm 5.3. skup A je kompaktan akko svaki niz u A ima konvergentan podniz ciji je limes u A.
Buduci je Cauch.niz u A ogranicen (jer je svaki Cauc.niz ogranicen), prema teoremu o nizovima (koji kaze da svaki ogranicen niz ima konvergentan podniz) Cauch.niz ima konvergentan podniz u A, pa iz Tm 5.3. zakljucujemo da je niz kompaktan. [/quote]
Po ovome ispada da je [tex]\mathbb{R}[/tex] kompaktan, iako znamo da nije. Dokaz ti propada jer umjesto opcenitog niza proucavas Cauchyev niz (pretpostavka teorema na koji se pozivas je da [u]svaki[/u] niz, ne samo Cauchyev, u A ima konvergentan podniz s limesom u A - u suprotnom ne bi bilo razlike izmedju kompaktnih i zatvorenih skupova). Trebas pokazati da svaki niz, bio on konvergentan ili ne, ima podniz s limesom u A. U ovom slucaju to neces moci pokazati jer kompaktni skupovi u [tex]\mathbb{R}^n[/tex] moraju biti omedjeni i zatvoreni, dok s druge strane postoje neomedjeni, zatvoreni i potpuni prostori, npr [tex]\mathbb{R}[/tex].
[quote]d) Da. Buduci je A kompaktan i f neprekidna, prema Tm 7.1., tada je f(A) kompaktan, a to znaci i zatvoren.[/quote]
Ovaj dokaz propada jer A ne mora biti kompaktan.
| frutabella (napisa): | | Zar definicija ne povlaci samo jednu stranu →, potpun je ako svaki cauchyev niz konvergira u njemu, ali ne znamo da li vrijedi obrat. |
Definicija nista ne povlaci. Definicija uvodi novi tremin, u ovom slucaju taj termin je potpun prostor. Kazemo da je prostor X potpun ako je svaki Cauchyev niz u X konvergentan u X. To je razlicito od "Ako je X potpun, onda je...". Prvo je definicija (rijec "kazemo" je kljucna), a drugo je izjava koja je istinita ili lazna.
| Citat: | c) Da. Prema Tm 5.3. skup A je kompaktan akko svaki niz u A ima konvergentan podniz ciji je limes u A.
Buduci je Cauch.niz u A ogranicen (jer je svaki Cauc.niz ogranicen), prema teoremu o nizovima (koji kaze da svaki ogranicen niz ima konvergentan podniz) Cauch.niz ima konvergentan podniz u A, pa iz Tm 5.3. zakljucujemo da je niz kompaktan. |
Po ovome ispada da je [tex]\mathbb{R}[/tex] kompaktan, iako znamo da nije. Dokaz ti propada jer umjesto opcenitog niza proucavas Cauchyev niz (pretpostavka teorema na koji se pozivas je da svaki niz, ne samo Cauchyev, u A ima konvergentan podniz s limesom u A - u suprotnom ne bi bilo razlike izmedju kompaktnih i zatvorenih skupova). Trebas pokazati da svaki niz, bio on konvergentan ili ne, ima podniz s limesom u A. U ovom slucaju to neces moci pokazati jer kompaktni skupovi u [tex]\mathbb{R}^n[/tex] moraju biti omedjeni i zatvoreni, dok s druge strane postoje neomedjeni, zatvoreni i potpuni prostori, npr [tex]\mathbb{R}[/tex].
| Citat: | | d) Da. Buduci je A kompaktan i f neprekidna, prema Tm 7.1., tada je f(A) kompaktan, a to znaci i zatvoren. |
Ovaj dokaz propada jer A ne mora biti kompaktan.
_________________
The Dude Abides
|
|
| [Vrh] |
|
frutabella
Forumaš(ica)

Pridružen/a: 09. 10. 2010. (16:35:36)
Postovi: (24E)16
|
 Postano: 4:44 ned, 4. 11. 2012 Naslov: Postano: 4:44 ned, 4. 11. 2012 Naslov: |
    |
|
|
Istina, gluposti pisem. Hvala.
2. zadatak gdje treba pokazati ogranicenost skupa
S= { (x,y)€R^2 : chx-1 <= y =< 1/(1+x^2)},
da li je dovoljno ovo chx-y<= 1 0<=1/(x^2) - y da bismo rekli da smo ogranicili varijable i da vrijedi x,y, € [0,1]?
Istina, gluposti pisem. Hvala.
2. zadatak gdje treba pokazati ogranicenost skupa
S= { (x,y)€R^2 : chx-1 ⇐ y =< 1/(1+x^2)},
da li je dovoljno ovo chx-y⇐ 1 0⇐1/(x^2) - y da bismo rekli da smo ogranicili varijable i da vrijedi x,y, € [0,1]?
|
|
| [Vrh] |
|
goranm
Forumaš(ica)


Pridružen/a: 12. 11. 2002. (20:09:12)
Postovi: (906)16
Spol: 
|
|
| [Vrh] |
|
frutabella
Forumaš(ica)

Pridružen/a: 09. 10. 2010. (16:35:36)
Postovi: (24E)16
|
 Postano: 5:02 ned, 4. 11. 2012 Naslov: Postano: 5:02 ned, 4. 11. 2012 Naslov: |
    |
|
|
[quote="goranm"][quote="frutabella"]da li je dovoljno ovo chx-y<= 1 0<=1/(x^2) - y da bismo rekli da smo ogranicili varijable i da vrijedi x,y, € [0,1]?[/quote]
Mozes li na temelju toga pronaci konkretan pravokutnik ili konkretnu kuglu koja obuhvaca citav skup?[/quote]
Naravno da ne. :oops:
Ali zato mogu sa ovim sigurno,
varijabla x:
chx-1>=0
1/(x^2)<=1 iz toga slijedi x € [0,1]
Ali imam i chx-1<=y<=1 ----> chx<=2 ----> |x|<= Arch2
varijabla y:
0<= y <= 1/(x^2) <= 1 pa je y€[0,1]
Znaci radijus kruznice bi onda trebao biti max ||(x,y)||?
8) Sto bi rekao asistent Vidak, ukljucite malo ono sto imate u svojim glavama. 8)
| goranm (napisa): | | frutabella (napisa): | | da li je dovoljno ovo chx-y⇐ 1 0⇐1/(x^2) - y da bismo rekli da smo ogranicili varijable i da vrijedi x,y, € [0,1]? |
Mozes li na temelju toga pronaci konkretan pravokutnik ili konkretnu kuglu koja obuhvaca citav skup? |
Naravno da ne. 
Ali zato mogu sa ovim sigurno,
varijabla x:
chx-1>=0
1/(x^2)⇐1 iz toga slijedi x € [0,1]
Ali imam i chx-1⇐y⇐1 ----> chx⇐2 ----> |x|⇐ Arch2
varijabla y:
0⇐ y ⇐ 1/(x^2) ⇐ 1 pa je y€[0,1]
Znaci radijus kruznice bi onda trebao biti max ||(x,y)||?
 Sto bi rekao asistent Vidak, ukljucite malo ono sto imate u svojim glavama. Sto bi rekao asistent Vidak, ukljucite malo ono sto imate u svojim glavama. 
|
|
| [Vrh] |
|
quark
Forumaš(ica)


Pridružen/a: 22. 10. 2011. (16:47:39)
Postovi: (DA)16
Spol: 
|
|
| [Vrh] |
|
pedro
Forumaš(ica)

Pridružen/a: 21. 10. 2010. (14:08:21)
Postovi: (19B)16
|
 Postano: 10:44 ned, 4. 11. 2012 Naslov: Postano: 10:44 ned, 4. 11. 2012 Naslov: |
    |
|
|
http://web.math.pmf.unizg.hr/nastava/difraf/dif/2010-11/kolokvij1%281%29.pdf
može 5 b) i c)
pod b) bi pokazala da je A povezan i onda bi slijedilo da je f(A) povezan jer je f neprekdina (ako ispadne da je povezano)
a kako onda za povezanost putevima, znamo da ako je A povezan putevima da je A povezan, vrijedi li obrat??
a pod c) nemam baš ideja kakve funckije bi uzela :S
[size=9][color=#999999]Added after 2 minutes:[/color][/size]
prema propoziciji 8.6, segment [a,b] podskup od R je povezan
vrijedi li onda da je segment [a,b] x [a,b] podskup od R^2 povezan?
http://web.math.pmf.unizg.hr/nastava/difraf/dif/2010-11/kolokvij1%281%29.pdf
može 5 b) i c)
pod b) bi pokazala da je A povezan i onda bi slijedilo da je f(A) povezan jer je f neprekdina (ako ispadne da je povezano)
a kako onda za povezanost putevima, znamo da ako je A povezan putevima da je A povezan, vrijedi li obrat??
a pod c) nemam baš ideja kakve funckije bi uzela :S
Added after 2 minutes:
prema propoziciji 8.6, segment [a,b] podskup od R je povezan
vrijedi li onda da je segment [a,b] x [a,b] podskup od R^2 povezan?
|
|
| [Vrh] |
|
pedro
Forumaš(ica)

Pridružen/a: 21. 10. 2010. (14:08:21)
Postovi: (19B)16
|
|
| [Vrh] |
|
ceps
Forumaš(ica)

Pridružen/a: 08. 10. 2010. (13:03:07)
Postovi: (13A)16
|
|
| [Vrh] |
|
slonic~tonic
Forumaš(ica)

Pridružen/a: 26. 10. 2011. (14:16:34)
Postovi: (84)16
Spol: 
|
|
| [Vrh] |
|
|











