Da ne bi bilo da ovakvo pitanje ostane neodgovereno na forumu iako te vise ne zanima ;)
Interval je otvoren, povezan skup u |R.
Otvoren skup se definira malo opcenitije. Definicija koja se radi prvi tjedan analize 3 jest preko kugle.
Dakle definiramo kuglu oko tocke [i]P0[/i] radijusa [i]r[/i] kao podskup nekog metrickog prostora [i]X[/i] na slijedeci nacin:
[latex]K(P_0, r)= \{P \in X:d(P,P_0)<r\}[/latex]
tj. kao skup tocaka udaljenih od sredista za strogo manje od r.
U terminima analize 1-2, tj skupa |R
[latex]K_R{(c, \varepsilon)}=\{x \in R : \vert x-c \vert < \varepsilon\}[/latex]
Tada definiramo otvoren skup (neka bude) [i]U[/i] kao skup za koji vrijedi:
[latex]\forall P \in U~ ~\exists \varepsilon_P>0~ t.d.~[/latex]
[latex]U = \bigcup_{P \in U~, ~\varepsilon_P>0}K(P, \varepsilon_P)[/latex]
..sto se pak moze interpretirati kao:
[list][*] skup koji se moze prikazati kao beskonacna unija kugli (iliti epsilon-okolina)
[*] skup kojem se oko svake tocke moze opisati kugla koja ce biti podskup toga skupa[/list:u]
Da ne bi bilo da ovakvo pitanje ostane neodgovereno na forumu iako te vise ne zanima 
Interval je otvoren, povezan skup u |R.
Otvoren skup se definira malo opcenitije. Definicija koja se radi prvi tjedan analize 3 jest preko kugle.
Dakle definiramo kuglu oko tocke P0 radijusa r kao podskup nekog metrickog prostora X na slijedeci nacin:
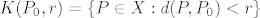
tj. kao skup tocaka udaljenih od sredista za strogo manje od r.
U terminima analize 1-2, tj skupa |R
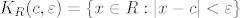
Tada definiramo otvoren skup (neka bude) U kao skup za koji vrijedi:
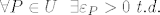
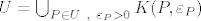
..sto se pak moze interpretirati kao:
- skup koji se moze prikazati kao beskonacna unija kugli (iliti epsilon-okolina)
- skup kojem se oko svake tocke moze opisati kugla koja ce biti podskup toga skupa
_________________

Pupoljak nije negiran. Rekao sam to i ponovit cu to jos jedanput. Pupoljak NIJE negirAn.
MADD
(Mothers Against Dirty Dialectics)
Based on a true story. NOT.
Ko ih sljivi, mi sviramo punk





