| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
kikzmyster
Forumaš(ica)

Pridružen/a: 14. 10. 2010. (13:35:08)
Postovi: (72)16
Spol: 
|
 Postano: 22:46 uto, 31. 1. 2012 Naslov: Postano: 22:46 uto, 31. 1. 2012 Naslov: |
    |
|
|
4.36. shvatio sam zadatak kao "u 128. cokoladi je kupon, ali mogao se i prije pojaviti kupon"
oznacimo s A - {128. cokolada je dobitna}
i uvodimo potpun sustav dogadaja Hi - {medu prvih 127 cokolada je bilo i dobitnih} [latex]\displaystyle i \in {0,1,2,...,50} [/latex]
Sad po formuli potpune vjerojatnosti je [latex]\displaystyle P(A) = \sum_{i=0}^{50}P(A|H_i)P(H_i) [/latex].
Pogledajmo kako izgleda P(A|Hi) i P(Hi), opcenito. Ako je u prvih 127 izvlacenja bilo [latex]\displaystyle i [/latex] dobitnih cokolada, onda je [latex]\displaystyle P(A|H_i) = \frac{50-i}{73} [/latex].
[latex]\displaystyle P(H_i) [/latex] je malo slozenija. P(Hi) je vjerojatnost da u slucanih 127 cokolada od ukupnih 200 bude bas i dobitnih od ukupno 50 dobitnih. dakle [latex]\displaystyle P(H_i) = \frac{\binom{50}{i}\binom{150}{127-i}}{\binom{200}{127}} [/latex] (kao hipergeometrijska). Dakle imamo [latex]\displaystyle P(A) = \sum_{i=0}^{50}\frac{50-i}{73}\frac{\binom{50}{i}\binom{150}{127-i}}{\binom{200}{127}} = \frac{\binom{200}{127}}{73}\sum_{i=0}^{50}(50-i)\binom{50}{i}\binom{150}{127-i} = [/latex]
[latex]\displaystyle \frac{50\binom{200}{127}}{73}\sum_{i=0}^{50}\binom{49}{i}\binom{150}{127-i} = (Vandermonde) = \frac{50\binom{200}{127}}{73}\binom{199}{127} [/latex].
4.44 b)
[latex]\diplaystyle P(C|C\cup D) = \frac{P(C\cap(C\cup D))}{P(C\cup D)} = \frac{P(C)}{P(C\cup D)} , P(C|D) = \frac{P(C\cap D)}{P(D)} [/latex]
dakle treba pokazati da vrijedi [latex] P(C)P(D) \ge P(C\cap D)P(C \cup D) [/latex]
[latex]\displaystyle \Leftrightarrow P(C)P(D) \ge (P(C)+P(D)-P(C\cap D))P(C\cap D) \Leftrightarrow [/latex]
[latex]\displaystyle P(C \cap D))^2 - (P(C)+P(D))P(C \cap D) + P(C)P(D) \ge 0 [/latex]
[latex]\displaystyle \Leftrightarrow (P(C\cap D) - P(C))(P(C\cap D)-P(D)) \ge 0 [/latex] sto vrijedi jer su oba izraza u zagradama <=0
EDIT: ipak, u 4.36 se najvjerojatnije misli na vjerojatnost da je TEK 128. dobitna, znaci sve ove prije nisu. Tad je rjesenje puno jednostavnije, [latex] P(A) = \frac{150}{200} \cdot\frac{149}{199} \cdot \frac{148}{198} \cdot \ldots \cdot\frac{24}{74} \cdot \frac{50}{73} [/latex]
127 puta otvara nedobitnu cokoladu, pa onda dobitnu. Cokolade se otvaraju samo jednom, zato ne znam bas za binomnu slucajnu varijablu kako su kolege spomenuli
4.36. shvatio sam zadatak kao "u 128. cokoladi je kupon, ali mogao se i prije pojaviti kupon"
oznacimo s A - {128. cokolada je dobitna}
i uvodimo potpun sustav dogadaja Hi - {medu prvih 127 cokolada je bilo i dobitnih} 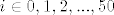
Sad po formuli potpune vjerojatnosti je 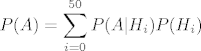 . .
Pogledajmo kako izgleda P(A|Hi) i P(Hi), opcenito. Ako je u prvih 127 izvlacenja bilo  dobitnih cokolada, onda je dobitnih cokolada, onda je 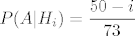 . .
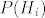 je malo slozenija. P(Hi) je vjerojatnost da u slucanih 127 cokolada od ukupnih 200 bude bas i dobitnih od ukupno 50 dobitnih. dakle je malo slozenija. P(Hi) je vjerojatnost da u slucanih 127 cokolada od ukupnih 200 bude bas i dobitnih od ukupno 50 dobitnih. dakle 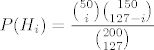 (kao hipergeometrijska). Dakle imamo (kao hipergeometrijska). Dakle imamo 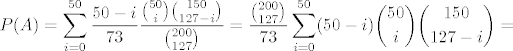
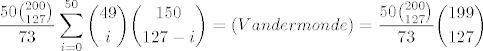 . .
4.44 b)
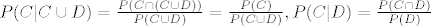
dakle treba pokazati da vrijedi 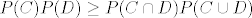
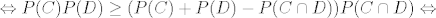
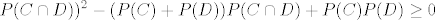
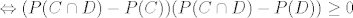 sto vrijedi jer su oba izraza u zagradama ⇐0 sto vrijedi jer su oba izraza u zagradama ⇐0
EDIT: ipak, u 4.36 se najvjerojatnije misli na vjerojatnost da je TEK 128. dobitna, znaci sve ove prije nisu. Tad je rjesenje puno jednostavnije, 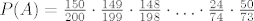
127 puta otvara nedobitnu cokoladu, pa onda dobitnu. Cokolade se otvaraju samo jednom, zato ne znam bas za binomnu slucajnu varijablu kako su kolege spomenuli
Zadnja promjena: kikzmyster; 13:52 ned, 10. 11. 2013; ukupno mijenjano 1 put.
|
|
| [Vrh] |
|
matijaB
Forumaš(ica)

Pridružen/a: 19. 08. 2010. (09:11:43)
Postovi: (4D)16
|
|
| [Vrh] |
|
Megy Poe
Forumaš(ica)

Pridružen/a: 05. 11. 2009. (23:14:52)
Postovi: (122)16
|
|
| [Vrh] |
|
Megy Poe
Forumaš(ica)

Pridružen/a: 05. 11. 2009. (23:14:52)
Postovi: (122)16
|
|
| [Vrh] |
|
kikzmyster
Forumaš(ica)

Pridružen/a: 14. 10. 2010. (13:35:08)
Postovi: (72)16
Spol: 
|
 Postano: 0:47 sri, 8. 2. 2012 Naslov: Postano: 0:47 sri, 8. 2. 2012 Naslov: |
    |
|
|
1.49
pretpostavimo suprotno, da su svi manji od 1/5, dakle [latex]\displaystyle P((A\cup B)^c) <\frac{1}{5} \Rightarrow P(A\cup B) >\frac{4}{5} [/latex]
[latex]\displaystyle P(A\cap B)<\frac{1}{5} [/latex]
[latex]\displaystyle P(A\bigtriangleup B)=P(A\cup B)-P(A\cap B) <\frac{1}{5} [/latex]
dakle imamo [latex]P(A \cup B) < \frac{1}{5} + P(A\cap B) < \frac{1}{5} + \frac{1}{5} = \frac{2}{5} [/latex], pa imamo kontradikciju.
1.50
[latex]\displaystyle A\cap B\cap C \subseteq A \Rightarrow P(A\cap B\cap C)\le P(A) [/latex]
[latex]\displaystyle A\cap B\cap C \subseteq B \Rightarrow P(A\cap B\cap C)\le P(B) [/latex]
[latex]\displaystyle A\cap B\cap C \subseteq C \Rightarrow P(A\cap B\cap C)\le P(C) [/latex]
dakle [latex]\displaystyle P(A\cap B\cap C)\le min\{P(A),P(B),P(C)\} [/latex]
isto tako ovo pod b), samo sto je nadskup.
1.53
uocimo da [latex]\displaystyle P(A_n)=1 \Rightarrow P(A_n^c) =0 [/latex]
sad imamo [latex]\displaystyle P(\bigcap_{n=1}^{\infty}A_n) = 1 - P((\bigcap_{n=1}^{\infty}A_n)^c) =[/latex]
[latex]\displaystyle 1 - P(\bigcup_{n=1}^{\infty}A_n^c) [/latex]
zbog sigma-poluaditivnosti imamo [latex]\displaystyle P(\bigcup_{n=1}^{\infty}A_n^c) \le \sum_{n=1}^{\infty}P((A_n)^c) = 0 [/latex] dakle [latex]\displaystyle P(\bigcap_{n=1}^{\infty}A_n) = 1- 0 = 1 [/latex]
1.54
K-A nejednakost kaze [latex]\displaystyle \frac{x_1 + x_2 +...+x_n}{n} \le \sqrt{\frac{x_1^2 + x_2^2 +...+ x_n^2}{n}} [/latex] za nenegativne x1,...,xn. pri tome jednakost vrijedi ako i samo ako su svi x-evi jednaki. Sad po ovoj nejednakosti imamo [latex] \displaystyle \sqrt{\frac{P(A\cap B)^2 + P(A^c \cap B)^2 + P(A \cap B^c)^2 + P(A^c \cap B^c)^2}{4}}[/latex][latex]\displaystyle \ge \frac{P(A\cap B) + P(A^c \cap B) + P(A \cap B^c) + P(A^c \cap B^c)}{4} [/latex]
Sad uocimo da [latex]\displaystyle P(A\cap B) + P(A^c \cap B) = P((A\cup A^c)\cap B) = P(\Omega \cap B) = P(B) [/latex] i isto tako [latex]\displaystyle P(A \cap B^c) + P(A^c \cap B^c) = P(B^c) [/latex]
dakle [latex]\displaystyle P(A\cap B) + P(A^c \cap B) + P(A \cap B^c) + P(A^c \cap B^c) = P(B\cup B^c) = P(\Omega) = 1 [/latex]
pa po onoj nejednakosti imamo [latex] \displaystyle \sqrt{\frac{P(A\cap B)^2 + P(A^c \cap B)^2 + P(A \cap B^c)^2 + P(A^c \cap B^c)^2}{4}} \ge \frac{1}{4} [/latex]
[latex] \displaystyle \Rightarrow \frac{P(A\cap B)^2 + P(A^c \cap B)^2 + P(A \cap B^c)^2 + P(A^c \cap B^c)^2}{4} \ge \frac{1}{16} [/latex]
[latex]\displaystyle \Rightarrow P(A\cap B)^2 + P(A^c \cap B)^2 + P(A \cap B^c)^2 + P(A^c \cap B^c)^2 \ge \frac{1}{4} [/latex] sto je prvi dio zadatka. Jednakost vrijedi ako i samo [latex]\displaystyle P(A\cap B) = P(A^c \cap B) = P(A \cap B^c) = P(A^c \cap B^c) [/latex] a kako je P(B) jednak zbroju prva dva, a P(B^c) jednak zbroju druga dva, zakljucujemo da jednakost vrijedi akko P(B)=P(B^c), dakle P(B) = 1- P(B) pa je P(B)=1/2. Analogno P(A)=1/2. Opet, jer je [latex]\displaystyle P(A\cap B) + P(A^c \cap B) = P(B) = \frac{1}{2} \Rightarrow P(A\cap B) =\frac{1}{4} [/latex]
1.49
pretpostavimo suprotno, da su svi manji od 1/5, dakle 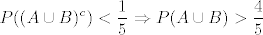
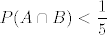
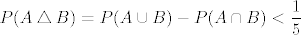
dakle imamo 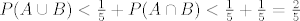 , pa imamo kontradikciju. , pa imamo kontradikciju.
1.50
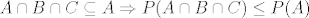
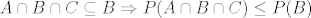
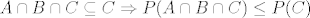
dakle 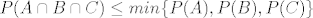
isto tako ovo pod b), samo sto je nadskup.
1.53
uocimo da 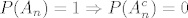
sad imamo 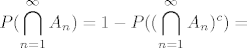
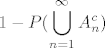
zbog sigma-poluaditivnosti imamo 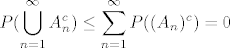 dakle dakle 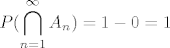
1.54
K-A nejednakost kaze 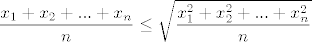 za nenegativne x1,...,xn. pri tome jednakost vrijedi ako i samo ako su svi x-evi jednaki. Sad po ovoj nejednakosti imamo za nenegativne x1,...,xn. pri tome jednakost vrijedi ako i samo ako su svi x-evi jednaki. Sad po ovoj nejednakosti imamo 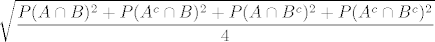 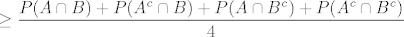
Sad uocimo da 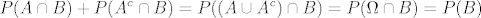 i isto tako i isto tako 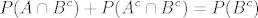
dakle 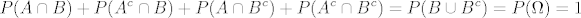
pa po onoj nejednakosti imamo 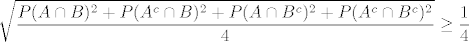
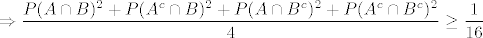
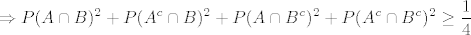 sto je prvi dio zadatka. Jednakost vrijedi ako i samo sto je prvi dio zadatka. Jednakost vrijedi ako i samo 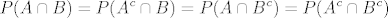 a kako je P(B) jednak zbroju prva dva, a P(B^c) jednak zbroju druga dva, zakljucujemo da jednakost vrijedi akko P(B)=P(B^c), dakle P(B) = 1- P(B) pa je P(B)=1/2. Analogno P(A)=1/2. Opet, jer je a kako je P(B) jednak zbroju prva dva, a P(B^c) jednak zbroju druga dva, zakljucujemo da jednakost vrijedi akko P(B)=P(B^c), dakle P(B) = 1- P(B) pa je P(B)=1/2. Analogno P(A)=1/2. Opet, jer je 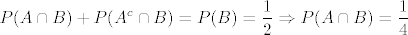
|
|
| [Vrh] |
|
maaajčiii
Forumaš(ica)

Pridružen/a: 05. 01. 2011. (12:11:11)
Postovi: (2D)16
|
 Postano: 1:05 sri, 8. 2. 2012 Naslov: Postano: 1:05 sri, 8. 2. 2012 Naslov: |
    |
|
|
jel može netko riješiti 1.30, 1.31, 1.34, 1.35, 1.36, 1.40 i 1.46?
http://web.math.pmf.unizg.hr/nastava/uuv/files/chap1.pdf
jel može netko riješiti 1.30, 1.31, 1.34, 1.35, 1.36, 1.40 i 1.46?
http://web.math.pmf.unizg.hr/nastava/uuv/files/chap1.pdf
|
|
| [Vrh] |
|
Megy Poe
Forumaš(ica)

Pridružen/a: 05. 11. 2009. (23:14:52)
Postovi: (122)16
|
|
| [Vrh] |
|
maaajčiii
Forumaš(ica)

Pridružen/a: 05. 01. 2011. (12:11:11)
Postovi: (2D)16
|
|
| [Vrh] |
|
kikzmyster
Forumaš(ica)

Pridružen/a: 14. 10. 2010. (13:35:08)
Postovi: (72)16
Spol: 
|
 Postano: 16:11 sri, 8. 2. 2012 Naslov: Postano: 16:11 sri, 8. 2. 2012 Naslov: |
    |
|
|
1.34
treba pokazat da vrijede ona tri definicijska svojstva sigma-algebre... evo redom
1) [latex]\displaystyle \emptyset \in F [/latex] jer je [latex]\displaystyle \emptyset^[/latex] prebrojiv skup.
2) Neka A iz F. Ako je A prebrojiv, onda je njegov komplement u omega neprebrojiv. Komplement tog komplementa je A, dakle prebrojiv skup, pa vrijedi [latex]\displaystyle A^c \in F [/latex] jer je njegov komplement prebrojiv. Ako je A takav da je A^c prebrojiv, onda je A^c u F jer za njega vrijedi "prebrojiv je".
3) Neka je [latex]\displaystyle A_n [/latex] niz dogadaja iz F. Nas zanima jeli [latex]\displaystyle \bigcup_{n=1}^{\infty}A_n \in F [/latex]. Gledamo dva slucaja... prvi slucaj, da su svi An prebrojivi. Tad je i ova unija u F, jer je prebrojiva unija prebrojivih skupova isto prebrojiv skup (googleaj "countable union of countable sets" ako te zanima zasto). Sad, ako medu An ima takvih da je An^c prebrojiv, onda gledamo [latex]\displaystyle (\bigcup_{n=1}^{\infty}A_n)^c [/latex], i zelimo dobiti da je taj skup prebrojiv. [latex]\displaystyle (\bigcup_{n=1}^{\infty}A_n)^c = \bigcap_{n=1}^{\infty}A_n^c [/latex]. Kako smo u slucaju da medu [latex]\displaystyle A_n^c [/latex] ima prebrojivih, ovaj presjek je prebrojiv skup, dakle [latex]\displaystyle \bigcup_{n=1}^{\infty}A_n \in F [/latex]
1.46
[latex]\displaystyle P(A_1 \cap ... \cap A_n) \ge P(A_1) +...+ P(A_n) - (n-1) [/latex]
[latex]\displaystyle \Leftrightarrow 1 - P(\bigcup_{i=1}^{n}A_i^c) \ge P(A_1) +...+ P(A_n) - (n-1) [/latex]
[latex]\displaystyle \Leftrightarrow P(A_1) +...+ P(A_n) + P(\bigcup_{i=1}^{n}A_i^c) \le n [/latex]
[latex]\displaystyle P(\bigcup_{i=1}^{n}A_i^c) \le \sum_{i=1}^{n}P(A_i^c) [/latex]
[latex]\displaystyle \Rightarrow \sum_{i=1}^{n}P(A_n) + P(\bigcup_{i=1}^{n}A_i^c) \le \sum_{i=1}^{n}P(A_n) + \sum_{i=1}^{n}P(A_n^c) [/latex]
[latex]\displaystyle = \sum_{i=1}^{n}(P(A_i)+P(A_i^c)) = n [/latex]
1.34
treba pokazat da vrijede ona tri definicijska svojstva sigma-algebre... evo redom
1) 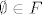 jer je jer je  prebrojiv skup. prebrojiv skup.
2) Neka A iz F. Ako je A prebrojiv, onda je njegov komplement u omega neprebrojiv. Komplement tog komplementa je A, dakle prebrojiv skup, pa vrijedi 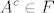 jer je njegov komplement prebrojiv. Ako je A takav da je A^c prebrojiv, onda je A^c u F jer za njega vrijedi "prebrojiv je". jer je njegov komplement prebrojiv. Ako je A takav da je A^c prebrojiv, onda je A^c u F jer za njega vrijedi "prebrojiv je".
3) Neka je 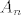 niz dogadaja iz F. Nas zanima jeli niz dogadaja iz F. Nas zanima jeli 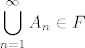 . Gledamo dva slucaja... prvi slucaj, da su svi An prebrojivi. Tad je i ova unija u F, jer je prebrojiva unija prebrojivih skupova isto prebrojiv skup (googleaj "countable union of countable sets" ako te zanima zasto). Sad, ako medu An ima takvih da je An^c prebrojiv, onda gledamo . Gledamo dva slucaja... prvi slucaj, da su svi An prebrojivi. Tad je i ova unija u F, jer je prebrojiva unija prebrojivih skupova isto prebrojiv skup (googleaj "countable union of countable sets" ako te zanima zasto). Sad, ako medu An ima takvih da je An^c prebrojiv, onda gledamo 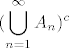 , i zelimo dobiti da je taj skup prebrojiv. , i zelimo dobiti da je taj skup prebrojiv. 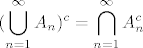 . Kako smo u slucaju da medu . Kako smo u slucaju da medu 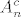 ima prebrojivih, ovaj presjek je prebrojiv skup, dakle ima prebrojivih, ovaj presjek je prebrojiv skup, dakle 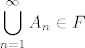
1.46
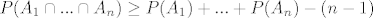
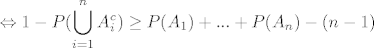
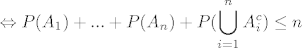
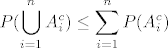
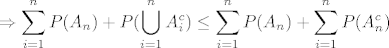
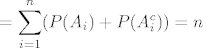
|
|
| [Vrh] |
|
PermutiranoPrase
Forumaš(ica)


Pridružen/a: 10. 09. 2011. (16:08:19)
Postovi: (F4)16
Spol: 
|
 Postano: 13:05 pon, 12. 11. 2012 Naslov: Postano: 13:05 pon, 12. 11. 2012 Naslov: |
    |
|
|
Nije mi jasno rješenje [url=http://web.math.pmf.unizg.hr/nastava/uuv/kolokviji/vjer-0809-kol1.pdf]2.b)[/url]. Zašto tako i zašto je ovo krivo? Stavila sam da imam ukupno [tex]4^6[/tex] mogućih riječi. Pogodnih riječi imam [tex]4^4[/tex]: ATA _ _ _, ova 3 slova mogu birati na [tex]4^3[/tex] načina, a ATA može početi na 1.mjestu, 2., 3. ili 4. To je ukupno [tex]4^4[/tex] načina, pa to podijelim.
Nije mi jasno rješenje 2.b). Zašto tako i zašto je ovo krivo? Stavila sam da imam ukupno [tex]4^6[/tex] mogućih riječi. Pogodnih riječi imam [tex]4^4[/tex]: ATA _ _ _, ova 3 slova mogu birati na [tex]4^3[/tex] načina, a ATA može početi na 1.mjestu, 2., 3. ili 4. To je ukupno [tex]4^4[/tex] načina, pa to podijelim.
|
|
| [Vrh] |
|
azra
Forumaš(ica)

Pridružen/a: 01. 05. 2005. (08:23:56)
Postovi: (89)16
|
|
| [Vrh] |
|
jaija
Forumaš(ica)

Pridružen/a: 12. 11. 2012. (15:59:39)
Postovi: (5)16
|
 Postano: 16:05 pon, 12. 11. 2012 Naslov: Postano: 16:05 pon, 12. 11. 2012 Naslov: |
    |
|
|
zamolio bih nekog ako mi može objasniti sljedeća dva zadatka, meni nikako ne ispadne točno rješenje, pa pp da krivo tumačim zadatke...
1. u ormaru su 4 para cipela. slučajno odaberemo 5 cipela. kolika je vjerojatnost da među izvučenim cipelama ima točno 1 par, a kolika je vjerojatnost da ima točno 2 para?
2. luster ima 5 grla za žarulje, 2 ispravnih, 3 neispravne. u grla stavljamo 5 žarulja od kojih su 2 ispravne 3 neispravne. kolika je vjerojatnost da ćemo uključivanjem lustera u struju dobiti svjetlo?
zamolio bih nekog ako mi može objasniti sljedeća dva zadatka, meni nikako ne ispadne točno rješenje, pa pp da krivo tumačim zadatke...
1. u ormaru su 4 para cipela. slučajno odaberemo 5 cipela. kolika je vjerojatnost da među izvučenim cipelama ima točno 1 par, a kolika je vjerojatnost da ima točno 2 para?
2. luster ima 5 grla za žarulje, 2 ispravnih, 3 neispravne. u grla stavljamo 5 žarulja od kojih su 2 ispravne 3 neispravne. kolika je vjerojatnost da ćemo uključivanjem lustera u struju dobiti svjetlo?
|
|
| [Vrh] |
|
mamba
Forumaš(ica)

Pridružen/a: 09. 07. 2012. (17:11:16)
Postovi: (16)16
|
|
| [Vrh] |
|
pedro
Forumaš(ica)

Pridružen/a: 21. 10. 2010. (14:08:21)
Postovi: (19B)16
|
 Postano: 23:23 pon, 12. 11. 2012 Naslov: Postano: 23:23 pon, 12. 11. 2012 Naslov: |
    |
|
|
http://web.math.pmf.unizg.hr/nastava/uuv/files/uuv-0607-kol1.pdf
ZAD 3.
Može pomoć sa sastavljanjem?
Ja sam uzela da je omega={jedno izvlačenje para (a,b) | a je iz 1 kutije, be je iz 2.kutije}
k(omega) = 20 * 20 =400
i sada bih definirala
[u]Nadite
vjerojatnost da ce se u 10 takvih izvlacenja barem jednom pojaviti svaki od ishoda:
(plava, plava), (bijela, bijela), (crvena, crvena), (zelena, zelena) i (zuta, zuta)![/u]
definirala kao potpun sistem događaja
H1 = {izvučen je par (C,C)}
H2 = {izvučen je par (P,P)}
H3 = {izvučen je par (Ž,Ž)}
H4 = {izvučen je par (B,B)}
ali nešto mi tu ne štima.
može pomoć?
http://web.math.pmf.unizg.hr/nastava/uuv/files/uuv-0607-kol1.pdf
ZAD 3.
Može pomoć sa sastavljanjem?
Ja sam uzela da je omega={jedno izvlačenje para (a,b) | a je iz 1 kutije, be je iz 2.kutije}
k(omega) = 20 * 20 =400
i sada bih definirala
Nadite
vjerojatnost da ce se u 10 takvih izvlacenja barem jednom pojaviti svaki od ishoda:
(plava, plava), (bijela, bijela), (crvena, crvena), (zelena, zelena) i (zuta, zuta)!
definirala kao potpun sistem događaja
H1 = {izvučen je par (C,C)}
H2 = {izvučen je par (P,P)}
H3 = {izvučen je par (Ž,Ž)}
H4 = {izvučen je par (B,B)}
ali nešto mi tu ne štima.
može pomoć?
|
|
| [Vrh] |
|
pedro
Forumaš(ica)

Pridružen/a: 21. 10. 2010. (14:08:21)
Postovi: (19B)16
|
|
| [Vrh] |
|
PermutiranoPrase
Forumaš(ica)


Pridružen/a: 10. 09. 2011. (16:08:19)
Postovi: (F4)16
Spol: 
|
|
| [Vrh] |
|
Deni001
Forumaš(ica)
Pridružen/a: 06. 09. 2011. (23:16:57)
Postovi: (23)16
Spol: 
|
|
| [Vrh] |
|
pedro
Forumaš(ica)

Pridružen/a: 21. 10. 2010. (14:08:21)
Postovi: (19B)16
|
|
| [Vrh] |
|
pedro
Forumaš(ica)

Pridružen/a: 21. 10. 2010. (14:08:21)
Postovi: (19B)16
|
|
| [Vrh] |
|
frutabella
Forumaš(ica)

Pridružen/a: 09. 10. 2010. (16:35:36)
Postovi: (24E)16
|
|
| [Vrh] |
|
|










