| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
pedro
Forumaš(ica)

Pridružen/a: 21. 10. 2010. (14:08:21)
Postovi: (19B)16
|
|
| [Vrh] |
|
grizly
Forumaš(ica)

Pridružen/a: 26. 01. 2011. (21:30:01)
Postovi: (27)16
Spol: 
|
 Postano: 16:18 uto, 6. 11. 2012 Naslov: Postano: 16:18 uto, 6. 11. 2012 Naslov: |
    |
|
|
Ako je A u tom skupu, onda je on ili konačan ili je komplement konačnog skupa (nema trećeg, tako je definiran ovaj "lijepo A"). U prvom slučaju Ac komplement od konačnog skupa (A je njegov komplement i po pretpostavci je konačan), a ako je A komplement konačnog skupa, onda je jasno Ac konačan skup pa je opet po definiciji i Ac u lijepom A.
Ovo drugo ti zapravo ide isto, samo se igraš sa skupovima, jedino je malo teže zapisati možda, ali ako shvaćaš prvi dio ne bi smio biti problem.
Ako je A u tom skupu, onda je on ili konačan ili je komplement konačnog skupa (nema trećeg, tako je definiran ovaj "lijepo A"). U prvom slučaju Ac komplement od konačnog skupa (A je njegov komplement i po pretpostavci je konačan), a ako je A komplement konačnog skupa, onda je jasno Ac konačan skup pa je opet po definiciji i Ac u lijepom A.
Ovo drugo ti zapravo ide isto, samo se igraš sa skupovima, jedino je malo teže zapisati možda, ali ako shvaćaš prvi dio ne bi smio biti problem.
_________________ Nit' sam normalna nit' se s takvima družim
 |
|
| [Vrh] |
|
pedro
Forumaš(ica)

Pridružen/a: 21. 10. 2010. (14:08:21)
Postovi: (19B)16
|
|
| [Vrh] |
|
pedro
Forumaš(ica)

Pridružen/a: 21. 10. 2010. (14:08:21)
Postovi: (19B)16
|
|
| [Vrh] |
|
Optimum
Forumaš(ica)

Pridružen/a: 07. 09. 2011. (09:16:23)
Postovi: (41)16
Spol: 
Lokacija: Zagreb
|
 Postano: 20:00 sri, 7. 11. 2012 Naslov: Postano: 20:00 sri, 7. 11. 2012 Naslov: |
    |
|
|
Pod a)
Na početku imamo 3 igrača na klupi i 5 igrača u igri.
Sad u 5. minuti trener izvadi jednog (tog kojeg mi promatramo) igrača, ostalo mu je još 35 minuta, ondnosno još 6 izmjena igrača.
U drugoj izmjeni može uzeti jednog od trojice na klupi, ali ovog našeg ne... to može na [dtex] \frac{2}{3} [/dtex] treću izmjenu opet jednog od ove dvojice, našeg trećeg ne dira, itd... tako šest puta:
[dtex] \frac{2}{3} \cdot \frac{2}{3} \cdot ... \cdot \frac{2}{3} = \frac{2^6}{3^6} [/dtex]
Pod a)
Na početku imamo 3 igrača na klupi i 5 igrača u igri.
Sad u 5. minuti trener izvadi jednog (tog kojeg mi promatramo) igrača, ostalo mu je još 35 minuta, ondnosno još 6 izmjena igrača.
U drugoj izmjeni može uzeti jednog od trojice na klupi, ali ovog našeg ne... to može na [dtex] \frac{2}{3} [/dtex] treću izmjenu opet jednog od ove dvojice, našeg trećeg ne dira, itd... tako šest puta:
[dtex] \frac{2}{3} \cdot \frac{2}{3} \cdot ... \cdot \frac{2}{3} = \frac{2^6}{3^6} [/dtex]
|
|
| [Vrh] |
|
student_92
Forumaš(ica)

Pridružen/a: 17. 09. 2011. (16:31:46)
Postovi: (B9)16
|
|
| [Vrh] |
|
quark
Forumaš(ica)


Pridružen/a: 22. 10. 2011. (16:47:39)
Postovi: (DA)16
Spol: 
|
 Postano: 21:27 pon, 12. 11. 2012 Naslov: Postano: 21:27 pon, 12. 11. 2012 Naslov: |
    |
|
|
[quote="student_92"]http://web.math.pmf.unizg.hr/nastava/uuv/kolokviji/vjer-0809-kol1.pdf
Zadatak 2. b) - nije mi jasno zašto se uopće ide na Sylvesterovu formulu.
Zašto se ne bi moglo ovako: Na 4 mjesta (1, 2, 3, 4) može početi riječ ATA, zatim na preostala 3 mjesta može doći svako od 4 ponuđena slova pa je rezultat [tex]\frac{4\cdot4\cdot4\cdot4}{4^6} = \frac{1}{4^2}[/tex]? Ovo što se radilo u rješenjima navodi me na razmišljanje da se traži samo jedno ponavljanje podniza ATA.[/quote]
Npr, gledaj što se događa ako imaš ATATAC - ako se ne varam, to brojiš dva puta.
[size=9]
P.S. Prvi put da mi se isplatilo gradivo regularnih izraza :lol: [/size]
| student_92 (napisa): | http://web.math.pmf.unizg.hr/nastava/uuv/kolokviji/vjer-0809-kol1.pdf
Zadatak 2. b) - nije mi jasno zašto se uopće ide na Sylvesterovu formulu.
Zašto se ne bi moglo ovako: Na 4 mjesta (1, 2, 3, 4) može početi riječ ATA, zatim na preostala 3 mjesta može doći svako od 4 ponuđena slova pa je rezultat [tex]\frac{4\cdot4\cdot4\cdot4}{4^6} = \frac{1}{4^2}[/tex]? Ovo što se radilo u rješenjima navodi me na razmišljanje da se traži samo jedno ponavljanje podniza ATA. |
Npr, gledaj što se događa ako imaš ATATAC - ako se ne varam, to brojiš dva puta.
P.S. Prvi put da mi se isplatilo gradivo regularnih izraza 
Zadnja promjena: quark; 23:33 pon, 12. 11. 2012; ukupno mijenjano 2 put/a.
|
|
| [Vrh] |
|
student_92
Forumaš(ica)

Pridružen/a: 17. 09. 2011. (16:31:46)
Postovi: (B9)16
|
|
| [Vrh] |
|
student_92
Forumaš(ica)

Pridružen/a: 17. 09. 2011. (16:31:46)
Postovi: (B9)16
|
|
| [Vrh] |
|
m_kao_marko
Forumaš(ica)

Pridružen/a: 14. 10. 2010. (21:05:03)
Postovi: (16)16
|
|
| [Vrh] |
|
Zenon
Forumaš(ica)


Pridružen/a: 09. 09. 2011. (19:14:43)
Postovi: (2B1)16
Sarma: -
Lokacija: [tex]\pm\infty[/tex]
|
|
| [Vrh] |
|
m_kao_marko
Forumaš(ica)

Pridružen/a: 14. 10. 2010. (21:05:03)
Postovi: (16)16
|
|
| [Vrh] |
|
Shaman
Forumaš(ica)


Pridružen/a: 24. 09. 2011. (22:21:43)
Postovi: (76)16
Spol: 
|
 Postano: 22:47 uto, 13. 11. 2012 Naslov: Postano: 22:47 uto, 13. 11. 2012 Naslov: |
    |
|
|
[quote="student_92"]Evo još jedno kratko. Trebam uputu (ako se nekome da, može i rješenje) za prva dva zadatka iz recimo prve grupe http://web.math.pmf.unizg.hr/nastava/uuv/files/uuv-0607-kol1.pdf .[/quote]
za prvi, vjerojatnost unije tih dogadjaja trebala bi biti manja ili jednaka 1 (podskup sigurnog dogadjaja), primijenis sigma aditivnost (u zadatku pise da su disjunktin) i npr integralnim cauchyjevim kriterijem se dobije da red divergira.
drugi, {B\A, A\B, (A presjek B), C} uzmes partitivan skup navedenog skupa tj. sve moguce unije ta 4 skupa i prazan skup.
za prvi, vjerojatnost unije tih dogadjaja trebala bi biti manja ili jednaka 1 (podskup sigurnog dogadjaja), primijenis sigma aditivnost (u zadatku pise da su disjunktin) i npr integralnim cauchyjevim kriterijem se dobije da red divergira.
drugi, {B\A, A\B, (A presjek B), C} uzmes partitivan skup navedenog skupa tj. sve moguce unije ta 4 skupa i prazan skup.
_________________
it was merely a setback
|
|
| [Vrh] |
|
pedro
Forumaš(ica)

Pridružen/a: 21. 10. 2010. (14:08:21)
Postovi: (19B)16
|
|
| [Vrh] |
|
Phoenix
Forumaš(ica)


Pridružen/a: 15. 05. 2010. (18:46:07)
Postovi: (164)16
Sarma: -
|
 Postano: 19:57 pon, 10. 12. 2012 Naslov: Postano: 19:57 pon, 10. 12. 2012 Naslov: |
    |
|
|
Smatramo da je igra poštena ako je očekivani dobitak nakon jedne partije (jedna partija sastoji se od dva bacanja novčića) bilo Marka bilo Ane točno [latex]0[/latex] kn (inače bi imali očekivanog pobjednika, što baš i nije pošteno). Primijetimo, ako je spomenuto očekivanje jednako [latex]c[/latex], a Marko i Ana su odigrali [latex]n[/latex] partija, očekivanje nakon cijele igre je [latex]nc[/latex], pa stoga i iz ovoga slijedi da mora biti [latex]c=0[/latex]. (O tome više dolje.)
Promotrimo Aninu igru. Iznos novca kojeg ima raste za [latex]6[/latex] kn s vjerojatnošću [latex]\frac{1}{2} \cdot \frac{1}{2} = \frac{1}{4}[/latex], a pada za [latex]a[/latex] kn (odnosno, porast je [latex]-a[/latex] kn) s vjerojatnošću [latex]1-\frac{1}{4}=\frac{3}{4}[/latex].
Slučajna varijabla koja modelira jednu partiju igre, nazovimo je [latex]X[/latex], dana je s [latex]X \sim \left( \begin{array}{c c}
-a & 6\\
\frac{3}{4} & \frac{1}{4} \\
\end{array}
\right)[/latex]. Računamo njeno očekivanje: [latex]\mathbb{E}X=-a \cdot \frac{3}{4}+6 \cdot \frac{1}{4} = \frac{-3a+6}{4}[/latex]
Kako mora vrijediti [latex]\mathbb{E}X=0[/latex], slijedi [latex]a=2[/latex].
Inače, ako želiš promatrati dobitak cjelokupne igre, neka je [latex]X_i[/latex] slučajna varijabla koja predstavlja Anin očekivani dobitak u [latex]i[/latex]-toj partiji igre od njih [latex]n[/latex], dakle [latex]1 \leq i \leq n[/latex]. Prema tome, za svaki [latex]i[/latex] vrijedi i [latex]X_i \sim X[/latex].
Sada je ukupno očekivanje u igri jednako [latex]\mathbb{E}[X_1+X_2+...+X_n]=\mathbb{E}X_1+\mathbb{E}X_2+...+\mathbb{E}X_n=n \cdot \mathbb{E}X[/latex], a to je ono što sam gore spominjao s brojem [latex]c[/latex].
Dakle, svejedno je promatraš li očekivanje nakon jedne partije ili nakon cijele igre. Sve zajedno se svodi na uvjet [latex]\mathbb{E}X=0[/latex]. :)
Smatramo da je igra poštena ako je očekivani dobitak nakon jedne partije (jedna partija sastoji se od dva bacanja novčića) bilo Marka bilo Ane točno  kn (inače bi imali očekivanog pobjednika, što baš i nije pošteno). Primijetimo, ako je spomenuto očekivanje jednako kn (inače bi imali očekivanog pobjednika, što baš i nije pošteno). Primijetimo, ako je spomenuto očekivanje jednako  , a Marko i Ana su odigrali , a Marko i Ana su odigrali  partija, očekivanje nakon cijele igre je partija, očekivanje nakon cijele igre je 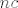 , pa stoga i iz ovoga slijedi da mora biti , pa stoga i iz ovoga slijedi da mora biti  . (O tome više dolje.) . (O tome više dolje.)
Promotrimo Aninu igru. Iznos novca kojeg ima raste za  kn s vjerojatnošću kn s vjerojatnošću 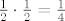 , a pada za , a pada za  kn (odnosno, porast je kn (odnosno, porast je 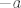 kn) s vjerojatnošću kn) s vjerojatnošću 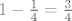 . .
Slučajna varijabla koja modelira jednu partiju igre, nazovimo je  , dana je s , dana je s 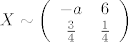 . Računamo njeno očekivanje: . Računamo njeno očekivanje: 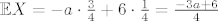
Kako mora vrijediti  , slijedi , slijedi 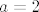 . .
Inače, ako želiš promatrati dobitak cjelokupne igre, neka je 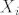 slučajna varijabla koja predstavlja Anin očekivani dobitak u slučajna varijabla koja predstavlja Anin očekivani dobitak u  -toj partiji igre od njih -toj partiji igre od njih  , dakle , dakle 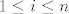 . Prema tome, za svaki . Prema tome, za svaki  vrijedi i vrijedi i 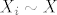 . .
Sada je ukupno očekivanje u igri jednako 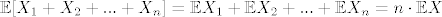 , a to je ono što sam gore spominjao s brojem , a to je ono što sam gore spominjao s brojem  . .
Dakle, svejedno je promatraš li očekivanje nakon jedne partije ili nakon cijele igre. Sve zajedno se svodi na uvjet  . . 
|
|
| [Vrh] |
|
sasha.f
Forumaš(ica)

Pridružen/a: 25. 10. 2011. (20:04:19)
Postovi: (3D)16
|
|
| [Vrh] |
|
student_92
Forumaš(ica)

Pridružen/a: 17. 09. 2011. (16:31:46)
Postovi: (B9)16
|
|
| [Vrh] |
|
rom
Forumaš(ica)
Pridružen/a: 26. 10. 2010. (11:10:35)
Postovi: (2D)16
|
|
| [Vrh] |
|
|








