| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
pedro
Forumaš(ica)

Pridružen/a: 21. 10. 2010. (14:08:21)
Postovi: (19B)16
|
 Postano: 11:03 uto, 18. 12. 2012 Naslov: 2. kolokvij Postano: 11:03 uto, 18. 12. 2012 Naslov: 2. kolokvij |
    |
|
|
http://web.math.pmf.unizg.hr/nastava/difraf/dif/2006-07/kolokvij_2.pdf
druga grupa, 1 zadatak.
ja sam dobila za rješenje 3 točke: (0,1,0) , (0,-1,0) i (1,0,0) a u rješenju zadataka (http://web.math.pmf.unizg.hr/nastava/difraf/dif/2006-07/kol2-rjesenja.pdf) je samo zapisano da je rješenje točka (1,0,0)
kada uvrstim točke u plohu jednadžbe sve dobro dobijem, tj točke se nalaze na plohi. gdje griješim?
http://web.math.pmf.unizg.hr/nastava/difraf/dif/2006-07/kolokvij_2.pdf
druga grupa, 1 zadatak.
ja sam dobila za rješenje 3 točke: (0,1,0) , (0,-1,0) i (1,0,0) a u rješenju zadataka (http://web.math.pmf.unizg.hr/nastava/difraf/dif/2006-07/kol2-rjesenja.pdf) je samo zapisano da je rješenje točka (1,0,0)
kada uvrstim točke u plohu jednadžbe sve dobro dobijem, tj točke se nalaze na plohi. gdje griješim?
|
|
| [Vrh] |
|
pedro
Forumaš(ica)

Pridružen/a: 21. 10. 2010. (14:08:21)
Postovi: (19B)16
|
 Postano: 12:59 uto, 18. 12. 2012 Naslov: Postano: 12:59 uto, 18. 12. 2012 Naslov: |
    |
|
|
zadatak 3 iz druge grupe
dobila sam da su stacionarne točke (0,0) i (1,1)
za (1,1) hesseova matrica je indefinitna, to znamo da je onda to sedlasta točka
a za (0,0) dobijem matricu sa samim 0 pa ne znamo kako da provjerimo karakter točke pa moramo na neki drugi način. kako je to najbolje provjeriti?
[size=9][color=#999999]Added after 47 minutes:[/color][/size]
4 zadatak.
imam problema s diferencijalom funkcije F: R^2-> R
F(y^3*z*x,y^2+x^2)
definiram h(x,y,z)=(y^3*z*x,y^2+x^2) h: R^3->R^2
i kada oću izračunati diferencijal od funkcije g= F(h(x,y,z)) muči me kako da napišem dif od F, treba mi ispasti 1x2 matrica a ispada mi 1x3 jer idemo po varijabli x,y i z, a zapravo bi trebala ići po dvije varijable a ne znam koje, help
zadatak 3 iz druge grupe
dobila sam da su stacionarne točke (0,0) i (1,1)
za (1,1) hesseova matrica je indefinitna, to znamo da je onda to sedlasta točka
a za (0,0) dobijem matricu sa samim 0 pa ne znamo kako da provjerimo karakter točke pa moramo na neki drugi način. kako je to najbolje provjeriti?
Added after 47 minutes:
4 zadatak.
imam problema s diferencijalom funkcije F: R^2→ R
F(y^3*z*x,y^2+x^2)
definiram h(x,y,z)=(y^3*z*x,y^2+x^2) h: R^3→R^2
i kada oću izračunati diferencijal od funkcije g= F(h(x,y,z)) muči me kako da napišem dif od F, treba mi ispasti 1x2 matrica a ispada mi 1x3 jer idemo po varijabli x,y i z, a zapravo bi trebala ići po dvije varijable a ne znam koje, help
|
|
| [Vrh] |
|
Phoenix
Forumaš(ica)


Pridružen/a: 15. 05. 2010. (18:46:07)
Postovi: (164)16
Sarma: -
|
 Postano: 13:31 uto, 18. 12. 2012 Naslov: Re: 2. kolokvij Postano: 13:31 uto, 18. 12. 2012 Naslov: Re: 2. kolokvij |
    |
|
|
1. Tangencijalne ravnine u točkama [tex](0,1,0)[/tex] i [tex](0,-1,0)[/tex] su, redom, [tex]y=1[/tex] i [tex]y=-1[/tex] (što se dobije uvrštavanjem [tex](x_0,y_0,z_0)=(0,\pm 1,0)[/tex] u drugu jednakost iz rješenja). Međutim, te ravnine ne sadržavaju točku [tex](0,0,1)[/tex].
Gdje točno griješiš, ne znam jer ne znam tvoj postupak i rješenje. Znam da si dobila neke točke plohe koje nisu traženo rješenje zadatka. :)
3. Možemo, primjerice, promatrati i analizirati funkciju pa vidjeti što se da iz prve zaključiti.
Prije svega, [tex]f(0,0)=0[/tex].
Sada, primijeti da je [tex]f(0,y)=\frac{4}{3}y^3[/tex], a preslikavanje [tex]y \mapsto \frac{4}{3}y^3[/tex] u nuli nema ni (lokalni) minimum ni maksimum.
Zaključujemo, za proizvoljnu okolinu [tex]U[/tex] od [tex]0[/tex], kako mora postojati [tex](0,y_1) \in U[/tex] i [tex](0,y_2) \in U[/tex] takve da je [tex]y_1>0[/tex] i [tex]y_2<0[/tex], vrijedi [tex]f(0,y_2)<f(0,0)<f(0,y_1)[/tex]. Stoga [tex](0,0)[/tex] nije lokalni ekstrem funkcije [tex]f[/tex].
4. Varijable nisu jednoznačne pa da moraš znati "preko kojih točno varijabli prikazati funkciju". Svejedno je je li [tex]f(x,y,z)[/tex] ili [tex]f(u,v,w)[/tex] ili [tex]f(a,b,c)[/tex], jer argumenti te funkcije su samo parametri, zamjene za konkretne vrijednosti.
(Ako ti iz nekog razloga i trebaju varijable da bi nekako zapisala [tex]F[/tex] u nekoj točki, stavi bilo koje i, zbog jasnoće, neka su različite od prethodno korištenih. Recimo, [tex]F(a,b)[/tex] ili [tex]F(u,v)[/tex] je sasvim dovoljno. Ali to ti i neće trebati za krajnje rješenje (ne smiješ ni imati u rješenju) - vidi dolje.)
Samo trebaš napisati sljedeće:
[tex]Dg(x,y,z)=DF(h(x,y,z))Dh(x,y,z)=DF(y^3zx,y^2+x^2) \begin{bmatrix} y^3z & 3y^2zx & y^3x \\ 2x & 2y & 0 \end{bmatrix}[/tex].
[tex]Dg(x,y,z)[/tex] mora biti matrica dimenzija [tex]1 \times 3[/tex], a [tex]DF(y^3zx,y^2+x^2)[/tex] dimenzija [tex]1 \times 2[/tex], što, zbog matričnog množenja s desne strane jednakosti, odgovara gornjoj formuli.
Ovo je i najdalje što možeš izračunati od diferencijala [tex]g[/tex] u točki jer ti [tex]F[/tex] nije zadan (samo znaš da je diferencijabilan na [tex]\mathbb{R}^2[/tex]).
1. Tangencijalne ravnine u točkama [tex](0,1,0)[/tex] i [tex](0,-1,0)[/tex] su, redom, [tex]y=1[/tex] i [tex]y=-1[/tex] (što se dobije uvrštavanjem [tex](x_0,y_0,z_0)=(0,\pm 1,0)[/tex] u drugu jednakost iz rješenja). Međutim, te ravnine ne sadržavaju točku [tex](0,0,1)[/tex].
Gdje točno griješiš, ne znam jer ne znam tvoj postupak i rješenje. Znam da si dobila neke točke plohe koje nisu traženo rješenje zadatka. 
3. Možemo, primjerice, promatrati i analizirati funkciju pa vidjeti što se da iz prve zaključiti.
Prije svega, [tex]f(0,0)=0[/tex].
Sada, primijeti da je [tex]f(0,y)=\frac{4}{3}y^3[/tex], a preslikavanje [tex]y \mapsto \frac{4}{3}y^3[/tex] u nuli nema ni (lokalni) minimum ni maksimum.
Zaključujemo, za proizvoljnu okolinu [tex]U[/tex] od [tex]0[/tex], kako mora postojati [tex](0,y_1) \in U[/tex] i [tex](0,y_2) \in U[/tex] takve da je [tex]y_1>0[/tex] i [tex]y_2<0[/tex], vrijedi [tex]f(0,y_2)<f(0,0)<f(0,y_1)[/tex]. Stoga [tex](0,0)[/tex] nije lokalni ekstrem funkcije [tex]f[/tex].
4. Varijable nisu jednoznačne pa da moraš znati "preko kojih točno varijabli prikazati funkciju". Svejedno je je li [tex]f(x,y,z)[/tex] ili [tex]f(u,v,w)[/tex] ili [tex]f(a,b,c)[/tex], jer argumenti te funkcije su samo parametri, zamjene za konkretne vrijednosti.
(Ako ti iz nekog razloga i trebaju varijable da bi nekako zapisala [tex]F[/tex] u nekoj točki, stavi bilo koje i, zbog jasnoće, neka su različite od prethodno korištenih. Recimo, [tex]F(a,b)[/tex] ili [tex]F(u,v)[/tex] je sasvim dovoljno. Ali to ti i neće trebati za krajnje rješenje (ne smiješ ni imati u rješenju) - vidi dolje.)
Samo trebaš napisati sljedeće:
[tex]Dg(x,y,z)=DF(h(x,y,z))Dh(x,y,z)=DF(y^3zx,y^2+x^2) \begin{bmatrix} y^3z & 3y^2zx & y^3x \\ 2x & 2y & 0 \end{bmatrix}[/tex].
[tex]Dg(x,y,z)[/tex] mora biti matrica dimenzija [tex]1 \times 3[/tex], a [tex]DF(y^3zx,y^2+x^2)[/tex] dimenzija [tex]1 \times 2[/tex], što, zbog matričnog množenja s desne strane jednakosti, odgovara gornjoj formuli.
Ovo je i najdalje što možeš izračunati od diferencijala [tex]g[/tex] u točki jer ti [tex]F[/tex] nije zadan (samo znaš da je diferencijabilan na [tex]\mathbb{R}^2[/tex]).
|
|
| [Vrh] |
|
pedro
Forumaš(ica)

Pridružen/a: 21. 10. 2010. (14:08:21)
Postovi: (19B)16
|
 Postano: 9:49 sri, 19. 12. 2012 Naslov: Re: 2. kolokvij Postano: 9:49 sri, 19. 12. 2012 Naslov: Re: 2. kolokvij |
    |
|
|
[quote="Phoenix"]1. Tangencijalne ravnine u točkama [tex](0,1,0)[/tex] i [tex](0,-1,0)[/tex] su, redom, [tex]y=1[/tex] i [tex]y=-1[/tex] (što se dobije uvrštavanjem [tex](x_0,y_0,z_0)=(0,\pm 1,0)[/tex] u drugu jednakost iz rješenja). Međutim, te ravnine ne sadržavaju točku [tex](0,0,1)[/tex].
Gdje točno griješiš, ne znam jer ne znam tvoj postupak i rješenje. Znam da si dobila neke točke plohe koje nisu traženo rješenje zadatka. :)
[/quote]
(to je 1 zadatak druge grupe)
ove jednadžbe sam dobila:
3z^2=0 (tang ravnina paralelna sa z-osi)
2x-2x^2=0 (tang rav porlazi točkom (1,0,0)
x^2+y^2+z^3-1=0 (točka se nalazi na plohi)
i dobijem tri rješenja:
(0,1,0)
(0,-1,0)
(1,0,0)
i u koji sad uvjet uvrštavamo točke da vidimo koja je točna?
| Phoenix (napisa): | 1. Tangencijalne ravnine u točkama [tex](0,1,0)[/tex] i [tex](0,-1,0)[/tex] su, redom, [tex]y=1[/tex] i [tex]y=-1[/tex] (što se dobije uvrštavanjem [tex](x_0,y_0,z_0)=(0,\pm 1,0)[/tex] u drugu jednakost iz rješenja). Međutim, te ravnine ne sadržavaju točku [tex](0,0,1)[/tex].
Gdje točno griješiš, ne znam jer ne znam tvoj postupak i rješenje. Znam da si dobila neke točke plohe koje nisu traženo rješenje zadatka. 
|
(to je 1 zadatak druge grupe)
ove jednadžbe sam dobila:
3z^2=0 (tang ravnina paralelna sa z-osi)
2x-2x^2=0 (tang rav porlazi točkom (1,0,0)
x^2+y^2+z^3-1=0 (točka se nalazi na plohi)
i dobijem tri rješenja:
(0,1,0)
(0,-1,0)
(1,0,0)
i u koji sad uvjet uvrštavamo točke da vidimo koja je točna?
|
|
| [Vrh] |
|
Phoenix
Forumaš(ica)


Pridružen/a: 15. 05. 2010. (18:46:07)
Postovi: (164)16
Sarma: -
|
 Postano: 10:13 sri, 19. 12. 2012 Naslov: Re: 2. kolokvij Postano: 10:13 sri, 19. 12. 2012 Naslov: Re: 2. kolokvij |
    |
|
|
Aha, u rješenjima i zadacima su obrnute grupe, to nisam primijetio. :P
Prva i treća jednadžba su ti OK, ali druga nije dobra. Naime, ako pokušavaš konstruirati tangencijalnu ravninu u točki plohe [tex](x_0,y_0,z_0)[/tex], vrijedi sljedeće:
[tex]2x_0(x-x_0)+2y_0(y-y_0)+3z_0^2(z-z_0)=0[/tex]
I sada, kako je [tex](1,0,0)[/tex] točka te ravnine, uvrštavamo [tex]x=1, y=0, z=0[/tex] i dobivamo:
[tex]2x_0(1-x_0)+2y_0(-y_0)+3z_0^2(-z_0)=0[/tex]
Popraviš li tu jednadžbu i riješiš li ovaj sustav triju jednadžbi, dobit ćeš za rješenje samo jednu točku i to onu danu u rješenju kolokvija. :)
Aha, u rješenjima i zadacima su obrnute grupe, to nisam primijetio. 
Prva i treća jednadžba su ti OK, ali druga nije dobra. Naime, ako pokušavaš konstruirati tangencijalnu ravninu u točki plohe [tex](x_0,y_0,z_0)[/tex], vrijedi sljedeće:
[tex]2x_0(x-x_0)+2y_0(y-y_0)+3z_0^2(z-z_0)=0[/tex]
I sada, kako je [tex](1,0,0)[/tex] točka te ravnine, uvrštavamo [tex]x=1, y=0, z=0[/tex] i dobivamo:
[tex]2x_0(1-x_0)+2y_0(-y_0)+3z_0^2(-z_0)=0[/tex]
Popraviš li tu jednadžbu i riješiš li ovaj sustav triju jednadžbi, dobit ćeš za rješenje samo jednu točku i to onu danu u rješenju kolokvija. 
|
|
| [Vrh] |
|
pedro
Forumaš(ica)

Pridružen/a: 21. 10. 2010. (14:08:21)
Postovi: (19B)16
|
 Postano: 10:14 sri, 19. 12. 2012 Naslov: Re: 2. kolokvij Postano: 10:14 sri, 19. 12. 2012 Naslov: Re: 2. kolokvij |
    |
|
|
[quote="Phoenix"]
3. Možemo, primjerice, promatrati i analizirati funkciju pa vidjeti što se da iz prve zaključiti.
Prije svega, [tex]f(0,0)=0[/tex].
Sada, primijeti da je [tex]f(0,y)=\frac{4}{3}y^3[/tex], a preslikavanje [tex]y \mapsto \frac{4}{3}y^3[/tex] u nuli nema ni (lokalni) minimum ni maksimum.
Zaključujemo, za proizvoljnu okolinu [tex]U[/tex] od [tex]0[/tex], kako mora postojati [tex](0,y_1) \in U[/tex] i [tex](0,y_2) \in U[/tex] takve da je [tex]y_1>0[/tex] i [tex]y_2<0[/tex], vrijedi [tex]f(0,y_2)<f(0,0)<f(0,y_1)[/tex]. Stoga [tex](0,0)[/tex] nije lokalni ekstrem funkcije [tex]f[/tex].
4. Varijable nisu jednoznačne pa da moraš znati "preko kojih točno varijabli prikazati funkciju". Svejedno je je li [tex]f(x,y,z)[/tex] ili [tex]f(u,v,w)[/tex] ili [tex]f(a,b,c)[/tex], jer argumenti te funkcije su samo parametri, zamjene za konkretne vrijednosti.
(Ako ti iz nekog razloga i trebaju varijable da bi nekako zapisala [tex]F[/tex] u nekoj točki, stavi bilo koje i, zbog jasnoće, neka su različite od prethodno korištenih. Recimo, [tex]F(a,b)[/tex] ili [tex]F(u,v)[/tex] je sasvim dovoljno. Ali to ti i neće trebati za krajnje rješenje (ne smiješ ni imati u rješenju) - vidi dolje.)
Samo trebaš napisati sljedeće:
[tex]Dg(x,y,z)=DF(h(x,y,z))Dh(x,y,z)=DF(y^3zx,y^2+x^2) \begin{bmatrix} y^3z & 3y^2zx & y^3x \\ 2x & 2y & 0 \end{bmatrix}[/tex].
[tex]Dg(x,y,z)[/tex] mora biti matrica dimenzija [tex]1 \times 3[/tex], a [tex]DF(y^3zx,y^2+x^2)[/tex] dimenzija [tex]1 \times 2[/tex], što, zbog matričnog množenja s desne strane jednakosti, odgovara gornjoj formuli.
Ovo je i najdalje što možeš izračunati od diferencijala [tex]g[/tex] u točki jer ti [tex]F[/tex] nije zadan (samo znaš da je diferencijabilan na [tex]\mathbb{R}^2[/tex]).[/quote]
3. JASNO! hvalaa :D
4.
http://web.math.pmf.unizg.hr/nastava/difraf/dif/p_o12.pdf
jeli dovoljno ovako zapisati kao što si ti ili bi trebalo još raspisati kao u primjeru 12.12?
jesmo li tim prikazom odmah pokazali da je g diferencijabilna? ili to moramo na neki drugi način komentirati?
[size=9][color=#999999]Added after 45 seconds:[/color][/size]
[quote="Phoenix"]Aha, u rješenjima i zadacima su obrnute grupe, to nisam primijetio. :P
Prva i treća jednadžba su ti OK, ali druga nije dobra. Naime, ako pokušavaš konstruirati tangencijalnu ravninu u točki plohe [tex](x_0,y_0,z_0)[/tex], vrijedi sljedeće:
[tex]2x_0(x-x_0)+2y_0(y-y_0)+3z_0^2(z-z_0)=0[/tex]
I sada, kako je [tex](1,0,0)[/tex] točka te ravnine, uvrštavamo [tex]x=1, y=0, z=0[/tex] i dobivamo:
[tex]2x_0(1-x_0)+2y_0(-y_0)+3z_0^2(-z_0)=0[/tex]
Popraviš li tu jednadžbu i riješiš li ovaj sustav triju jednadžbi, dobit ćeš za rješenje samo jednu točku i to onu danu u rješenju kolokvija. :)[/quote]
aaaaaa, jesam li blentavaaaaaaaaa hahahahaha hvala puno !
| Phoenix (napisa): |
3. Možemo, primjerice, promatrati i analizirati funkciju pa vidjeti što se da iz prve zaključiti.
Prije svega, [tex]f(0,0)=0[/tex].
Sada, primijeti da je [tex]f(0,y)=\frac{4}{3}y^3[/tex], a preslikavanje [tex]y \mapsto \frac{4}{3}y^3[/tex] u nuli nema ni (lokalni) minimum ni maksimum.
Zaključujemo, za proizvoljnu okolinu [tex]U[/tex] od [tex]0[/tex], kako mora postojati [tex](0,y_1) \in U[/tex] i [tex](0,y_2) \in U[/tex] takve da je [tex]y_1>0[/tex] i [tex]y_2<0[/tex], vrijedi [tex]f(0,y_2)<f(0,0)<f(0,y_1)[/tex]. Stoga [tex](0,0)[/tex] nije lokalni ekstrem funkcije [tex]f[/tex].
4. Varijable nisu jednoznačne pa da moraš znati "preko kojih točno varijabli prikazati funkciju". Svejedno je je li [tex]f(x,y,z)[/tex] ili [tex]f(u,v,w)[/tex] ili [tex]f(a,b,c)[/tex], jer argumenti te funkcije su samo parametri, zamjene za konkretne vrijednosti.
(Ako ti iz nekog razloga i trebaju varijable da bi nekako zapisala [tex]F[/tex] u nekoj točki, stavi bilo koje i, zbog jasnoće, neka su različite od prethodno korištenih. Recimo, [tex]F(a,b)[/tex] ili [tex]F(u,v)[/tex] je sasvim dovoljno. Ali to ti i neće trebati za krajnje rješenje (ne smiješ ni imati u rješenju) - vidi dolje.)
Samo trebaš napisati sljedeće:
[tex]Dg(x,y,z)=DF(h(x,y,z))Dh(x,y,z)=DF(y^3zx,y^2+x^2) \begin{bmatrix} y^3z & 3y^2zx & y^3x \\ 2x & 2y & 0 \end{bmatrix}[/tex].
[tex]Dg(x,y,z)[/tex] mora biti matrica dimenzija [tex]1 \times 3[/tex], a [tex]DF(y^3zx,y^2+x^2)[/tex] dimenzija [tex]1 \times 2[/tex], što, zbog matričnog množenja s desne strane jednakosti, odgovara gornjoj formuli.
Ovo je i najdalje što možeš izračunati od diferencijala [tex]g[/tex] u točki jer ti [tex]F[/tex] nije zadan (samo znaš da je diferencijabilan na [tex]\mathbb{R}^2[/tex]). |
3. JASNO! hvalaa 
4.
http://web.math.pmf.unizg.hr/nastava/difraf/dif/p_o12.pdf
jeli dovoljno ovako zapisati kao što si ti ili bi trebalo još raspisati kao u primjeru 12.12?
jesmo li tim prikazom odmah pokazali da je g diferencijabilna? ili to moramo na neki drugi način komentirati?
Added after 45 seconds:
| Phoenix (napisa): | Aha, u rješenjima i zadacima su obrnute grupe, to nisam primijetio. 
Prva i treća jednadžba su ti OK, ali druga nije dobra. Naime, ako pokušavaš konstruirati tangencijalnu ravninu u točki plohe [tex](x_0,y_0,z_0)[/tex], vrijedi sljedeće:
[tex]2x_0(x-x_0)+2y_0(y-y_0)+3z_0^2(z-z_0)=0[/tex]
I sada, kako je [tex](1,0,0)[/tex] točka te ravnine, uvrštavamo [tex]x=1, y=0, z=0[/tex] i dobivamo:
[tex]2x_0(1-x_0)+2y_0(-y_0)+3z_0^2(-z_0)=0[/tex]
Popraviš li tu jednadžbu i riješiš li ovaj sustav triju jednadžbi, dobit ćeš za rješenje samo jednu točku i to onu danu u rješenju kolokvija.  |
aaaaaa, jesam li blentavaaaaaaaaa hahahahaha hvala puno !
|
|
| [Vrh] |
|
Phoenix
Forumaš(ica)


Pridružen/a: 15. 05. 2010. (18:46:07)
Postovi: (164)16
Sarma: -
|
 Postano: 10:26 sri, 19. 12. 2012 Naslov: Re: 2. kolokvij Postano: 10:26 sri, 19. 12. 2012 Naslov: Re: 2. kolokvij |
    |
|
|
4. Zadnja dva reda s linka ti ne trebaju. :)
Ali isto tako, ako te pita da prokomentiraš diferencijabilnost funkcije, napisao bih da je kao kompozicija dviju diferencijabilnih također diferencijabilna - to su [tex]F[/tex], po tvrdnji iz zadatka, te pomoćna funkcija [tex]h[/tex] jer su joj funkcije komponente diferencijabilne. A one su diferencijabilne kao produkt, zbroj (ili nešto treće) funkcija projekcija ([tex](x,y) \mapsto x[/tex] ili [tex](x,y) \mapsto y[/tex]) koje su diferencijabilne. Tako nekako. :D
Nije bitno da ovo objašnjenje bude preformalno. S jedne strane, da se vidi da znaš nabrojati da je po produktu, kompoziciji, kvocijentu, čemu već ne, diferencijabilna i to bih naveo. S druge strane, ipak nije lako posvetiti poveći paragraf te dragocjeno vrijeme na takvo objašnjenje - recimo, da umjesto "diferencijabilno" pišeš jednostavno "dfb" i slično. :)
4. Zadnja dva reda s linka ti ne trebaju. 
Ali isto tako, ako te pita da prokomentiraš diferencijabilnost funkcije, napisao bih da je kao kompozicija dviju diferencijabilnih također diferencijabilna - to su [tex]F[/tex], po tvrdnji iz zadatka, te pomoćna funkcija [tex]h[/tex] jer su joj funkcije komponente diferencijabilne. A one su diferencijabilne kao produkt, zbroj (ili nešto treće) funkcija projekcija ([tex](x,y) \mapsto x[/tex] ili [tex](x,y) \mapsto y[/tex]) koje su diferencijabilne. Tako nekako. 
Nije bitno da ovo objašnjenje bude preformalno. S jedne strane, da se vidi da znaš nabrojati da je po produktu, kompoziciji, kvocijentu, čemu već ne, diferencijabilna i to bih naveo. S druge strane, ipak nije lako posvetiti poveći paragraf te dragocjeno vrijeme na takvo objašnjenje - recimo, da umjesto "diferencijabilno" pišeš jednostavno "dfb" i slično. 
|
|
| [Vrh] |
|
pedro
Forumaš(ica)

Pridružen/a: 21. 10. 2010. (14:08:21)
Postovi: (19B)16
|
 Postano: 10:32 sri, 19. 12. 2012 Naslov: Postano: 10:32 sri, 19. 12. 2012 Naslov: |
    |
|
|
e hvala :)
još sad imam samo problem s 2. zadatkom za (x,y) = (0,0)
dobijem da postoje parcijalne u (0,0) i da je jedini kandidat za diferencijal Df(0,0)=0
e sad me zeza limes, pretpostavljam da treba pomoću tm o sendviču a nemrem nikak ocjenit :S
ne znam koristit latex pa se neću ni trudit onako ružno napisati funkciju.
e hvala 
još sad imam samo problem s 2. zadatkom za (x,y) = (0,0)
dobijem da postoje parcijalne u (0,0) i da je jedini kandidat za diferencijal Df(0,0)=0
e sad me zeza limes, pretpostavljam da treba pomoću tm o sendviču a nemrem nikak ocjenit :S
ne znam koristit latex pa se neću ni trudit onako ružno napisati funkciju.
|
|
| [Vrh] |
|
Phoenix
Forumaš(ica)


Pridružen/a: 15. 05. 2010. (18:46:07)
Postovi: (164)16
Sarma: -
|
 Postano: 11:22 sri, 19. 12. 2012 Naslov: Postano: 11:22 sri, 19. 12. 2012 Naslov: |
    |
|
|
Želiš pokazati vrijedi li:
[dtex]\displaystyle \lim_{(x,y) \rightarrow (0,0)} \frac{x^2y}{(x^2+y^2)^{\frac{3}{2}}}=0.[/dtex]
Za [tex](x_n,y_n)=(\frac{1}{n},\frac{1}{n})[/tex] vrijedi [dtex]\frac{x_n^2y_n}{(x_n^2+y_n^2)^{\frac{3}{2}}}=\frac{\frac{1}{n^3}}{\frac{2\sqrt{2}}{n^3}}=\frac{1}{2\sqrt{2}}.[/dtex]
Dakle, postoji niz koji konvergira prema nuli za koji razlomak ne konvergira prema nuli. Samim time, limes ne može biti jednak [tex]0[/tex].
(Možeš, kao i prije, uvrstiti još jedan niz i pokazati da limes i ne postoji, no to nije potrebno kod ovog zadatka.)
Dakle, [tex]f[/tex] nije diferencijabilna u [tex](0,0)[/tex].
Želiš pokazati vrijedi li:
[dtex]\displaystyle \lim_{(x,y) \rightarrow (0,0)} \frac{x^2y}{(x^2+y^2)^{\frac{3}{2}}}=0.[/dtex]
Za [tex](x_n,y_n)=(\frac{1}{n},\frac{1}{n})[/tex] vrijedi [dtex]\frac{x_n^2y_n}{(x_n^2+y_n^2)^{\frac{3}{2}}}=\frac{\frac{1}{n^3}}{\frac{2\sqrt{2}}{n^3}}=\frac{1}{2\sqrt{2}}.[/dtex]
Dakle, postoji niz koji konvergira prema nuli za koji razlomak ne konvergira prema nuli. Samim time, limes ne može biti jednak [tex]0[/tex].
(Možeš, kao i prije, uvrstiti još jedan niz i pokazati da limes i ne postoji, no to nije potrebno kod ovog zadatka.)
Dakle, [tex]f[/tex] nije diferencijabilna u [tex](0,0)[/tex].
|
|
| [Vrh] |
|
pedro
Forumaš(ica)

Pridružen/a: 21. 10. 2010. (14:08:21)
Postovi: (19B)16
|
|
| [Vrh] |
|
pedro
Forumaš(ica)

Pridružen/a: 21. 10. 2010. (14:08:21)
Postovi: (19B)16
|
 Postano: 10:48 pet, 21. 12. 2012 Naslov: Postano: 10:48 pet, 21. 12. 2012 Naslov: |
    |
|
|
http://web.math.pmf.unizg.hr/nastava/difraf/dif/2010-11/kolokvij1.pdf
kako točno radim 1 zad?
znači moram provjeriti neprekidnost i derivabilnost funkcije, jel tako?
gledam posebno za točke oblika (0,y) i one koje su različite od (0,y) i tražim parcijalne derivacije, ako postoje i neprekidne su onda je funkcija diferencijabilna. a kako provjerim neprekidnost?
[size=9][color=#999999]Added after 23 minutes:[/color][/size]
može pomoć s limesom za točke oblika (0,y) y iz R
dobila sam da postoje parcijalne derivacije i da je jedinikandidat za diferencijal Df(0,y) = [y 0]
i onaj limes nikak da uspijem rješit :S
http://web.math.pmf.unizg.hr/nastava/difraf/dif/2010-11/kolokvij1.pdf
kako točno radim 1 zad?
znači moram provjeriti neprekidnost i derivabilnost funkcije, jel tako?
gledam posebno za točke oblika (0,y) i one koje su različite od (0,y) i tražim parcijalne derivacije, ako postoje i neprekidne su onda je funkcija diferencijabilna. a kako provjerim neprekidnost?
Added after 23 minutes:
može pomoć s limesom za točke oblika (0,y) y iz R
dobila sam da postoje parcijalne derivacije i da je jedinikandidat za diferencijal Df(0,y) = [y 0]
i onaj limes nikak da uspijem rješit :S
|
|
| [Vrh] |
|
pedro
Forumaš(ica)

Pridružen/a: 21. 10. 2010. (14:08:21)
Postovi: (19B)16
|
|
| [Vrh] |
|
Loo
Forumaš(ica)


Pridružen/a: 11. 06. 2012. (16:02:07)
Postovi: (D0)16
Spol: 
|
 Postano: 10:13 sub, 22. 12. 2012 Naslov: Postano: 10:13 sub, 22. 12. 2012 Naslov: |
    |
|
|
funkcija je diferencijabilna jer je umnožak i suma diferencijabilnih.
ajmo sada izračunati parcijalne derivacije.
[tex]\partial _kf(x_1,...,x_n)=\displaystyle\sum_{i=1, i\neq k}^{n}x_i[/tex]
sada ću pokazati zašto:
[tex]\displaystyle\sum_{1\leq i < j\leq n}x_ix_j=\displaystyle\sum _{i=1}^{n}x_i \displaystyle\sum _{j=i+1}^{n}x_j=\displaystyle\sum _{i=1}^{k}x_i\displaystyle\sum _{j=i+1}^{n}x_j + \displaystyle\sum _{i=k+1}^{n} x_i \displaystyle\sum _{j=i+1}^{n} x_j[/tex]
kada parcijalno deriviramo po [tex]x_k[/tex], ova druga suma biti će [tex]0[/tex] jer se [tex]x_k[/tex] u njoj uopće ne pojavljuje, a kada prvu malo raspišeš, vidjet ćeš da je ona jednaka [tex]x_1(x_2+...+x_k+...+x_n)+x_2(x_3+...+x_k+...+x_n)+...+x_k(x_{k+1}+...+x_n)[/tex] i kada to parcijalno deriviraš dobiješ upravo ovo što sam gore napisala.
dobro, ajmo sad izračunati [tex]Df(x)(x)[/tex].
budući da je funkcija realna djelovanje diferencijala na neki vektor ekvivalentno je skalarnom množenju gradijenta s tim vektorom.
dakle
[tex]Df(x)(x)=((\displaystyle\sum_{i=2}^{n}x_i, \displaystyle\sum_{i=1, i\neq 2}^{n}x_i,..., \displaystyle\sum_{i=1}^{n-1}x_i)|(x_1,..., x_n))=\displaystyle\sum_{j=1}^{n}x_j\displaystyle\sum_{i=1, i\neq j}^{n}x_i = \displaystyle\sum_{j=1}^{n}x_j\displaystyle\sum_{i=1}^{j-1}x_i + \displaystyle\sum_{j=1}^{n}x_j\displaystyle\sum_{i=j+1}^{n}x_i=\displaystyle\sum_{1\leq i<j \leq n}x_ix_j + \displaystyle\sum_{1\leq j<i \leq n}x_ix_j[/tex]
zamjenom indeksa u drugoj sumi dobivamo da je to upravo
[tex]\displaystyle2\sum_{1\leq i<j \leq n}x_ix_j[/tex]
EDIT: aha zaboravila sam napisati što je diferencijal, odnosno njegov matrični prikaz. pa to je [tex]1\times n[/tex] matrica s koordinatama [tex]\partial _kf[/tex]. vidi gradijent :)
funkcija je diferencijabilna jer je umnožak i suma diferencijabilnih.
ajmo sada izračunati parcijalne derivacije.
[tex]\partial _kf(x_1,...,x_n)=\displaystyle\sum_{i=1, i\neq k}^{n}x_i[/tex]
sada ću pokazati zašto:
[tex]\displaystyle\sum_{1\leq i < j\leq n}x_ix_j=\displaystyle\sum _{i=1}^{n}x_i \displaystyle\sum _{j=i+1}^{n}x_j=\displaystyle\sum _{i=1}^{k}x_i\displaystyle\sum _{j=i+1}^{n}x_j + \displaystyle\sum _{i=k+1}^{n} x_i \displaystyle\sum _{j=i+1}^{n} x_j[/tex]
kada parcijalno deriviramo po [tex]x_k[/tex], ova druga suma biti će [tex]0[/tex] jer se [tex]x_k[/tex] u njoj uopće ne pojavljuje, a kada prvu malo raspišeš, vidjet ćeš da je ona jednaka [tex]x_1(x_2+...+x_k+...+x_n)+x_2(x_3+...+x_k+...+x_n)+...+x_k(x_{k+1}+...+x_n)[/tex] i kada to parcijalno deriviraš dobiješ upravo ovo što sam gore napisala.
dobro, ajmo sad izračunati [tex]Df(x)(x)[/tex].
budući da je funkcija realna djelovanje diferencijala na neki vektor ekvivalentno je skalarnom množenju gradijenta s tim vektorom.
dakle
[tex]Df(x)(x)=((\displaystyle\sum_{i=2}^{n}x_i, \displaystyle\sum_{i=1, i\neq 2}^{n}x_i,..., \displaystyle\sum_{i=1}^{n-1}x_i)|(x_1,..., x_n))=\displaystyle\sum_{j=1}^{n}x_j\displaystyle\sum_{i=1, i\neq j}^{n}x_i = \displaystyle\sum_{j=1}^{n}x_j\displaystyle\sum_{i=1}^{j-1}x_i + \displaystyle\sum_{j=1}^{n}x_j\displaystyle\sum_{i=j+1}^{n}x_i=\displaystyle\sum_{1\leq i<j \leq n}x_ix_j + \displaystyle\sum_{1\leq j<i \leq n}x_ix_j[/tex]
zamjenom indeksa u drugoj sumi dobivamo da je to upravo
[tex]\displaystyle2\sum_{1\leq i<j \leq n}x_ix_j[/tex]
EDIT: aha zaboravila sam napisati što je diferencijal, odnosno njegov matrični prikaz. pa to je [tex]1\times n[/tex] matrica s koordinatama [tex]\partial _kf[/tex]. vidi gradijent 
|
|
| [Vrh] |
|
pedro
Forumaš(ica)

Pridružen/a: 21. 10. 2010. (14:08:21)
Postovi: (19B)16
|
 Postano: 10:59 sub, 22. 12. 2012 Naslov: Postano: 10:59 sub, 22. 12. 2012 Naslov: |
    |
|
|
[quote="Loo"]funkcija je diferencijabilna jer je umnožak i suma diferencijabilnih.
ajmo sada izračunati parcijalne derivacije.
[tex]\partial _kf(x_1,...,x_n)=\displaystyle\sum_{i=1, i\neq k}^{n}x_i[/tex]
sada ću pokazati zašto:
[tex]\displaystyle\sum_{1\leq i < j\leq n}x_ix_j=\displaystyle\sum _{i=1}^{n}x_i \displaystyle\sum _{j=i+1}^{n}x_j=\displaystyle\sum _{i=1}^{k}x_i\displaystyle\sum _{j=i+1}^{n}x_j + \displaystyle\sum _{i=k+1}^{n} x_i \displaystyle\sum _{j=i+1}^{n} x_j[/tex]
kada parcijalno deriviramo po [tex]x_k[/tex], ova druga suma biti će [tex]0[/tex] jer se [tex]x_k[/tex] u njoj uopće ne pojavljuje, a kada prvu malo raspišeš, vidjet ćeš da je ona jednaka [tex]x_1(x_2+...+x_k+...+x_n)+x_2(x_3+...+x_k+...+x_n)+...+x_k(x_{k+1}+...+x_n)[/tex] i kada to parcijalno deriviraš dobiješ upravo ovo što sam gore napisala.
dobro, ajmo sad izračunati [tex]Df(x)(x)[/tex].
budući da je funkcija realna djelovanje diferencijala na neki vektor ekvivalentno je skalarnom množenju gradijenta s tim vektorom.
dakle
[tex]Df(x)(x)=((\displaystyle\sum_{i=2}^{n}x_i, \displaystyle\sum_{i=1, i\neq 2}^{n}x_i,..., \displaystyle\sum_{i=1}^{n-1}x_i)|(x_1,..., x_n))=\displaystyle\sum_{j=1}^{n}x_j\displaystyle\sum_{i=1, i\neq j}^{n}x_i = \displaystyle\sum_{j=1}^{n}x_j\displaystyle\sum_{i=1}^{j-1}x_i + \displaystyle\sum_{j=1}^{n}x_j\displaystyle\sum_{i=j+1}^{n}x_i=\displaystyle\sum_{1\leq i<j \leq n}x_ix_j + \displaystyle\sum_{1\leq j<i \leq n}x_ix_j[/tex]
zamjenom indeksa u drugoj sumi dobivamo da je to upravo
[tex]\displaystyle2\sum_{1\leq i<j \leq n}x_ix_j[/tex]
EDIT: aha zaboravila sam napisati što je diferencijal, odnosno njegov matrični prikaz. pa to je [tex]1\times n[/tex] matrica s koordinatama [tex]\partial _kf[/tex]. vidi gradijent :)[/quote]
mislim da ti nije dobro jer index i ti mora biti manji od j
ja sam dobila ovako za diferencijal:
[latex]\begin{bmatrix}
\sum_{i=2}^{n} xi&\sum_{i=3}^{n} xi &\sum_{i=4}^{n} xi & ...& & xn & 0 &
\end{bmatrix}[/latex]
[size=9][color=#999999]Added after 1 minutes:[/color][/size]
ja sam za pokazati diferencijabilnost išla to pomoću definicije. Jeli okej samo ovako komentirati zašto je funkcija dfb(vidi se) ili se mora pomoću def? jer piše "pokažite da je fun dfb..."
| Loo (napisa): | funkcija je diferencijabilna jer je umnožak i suma diferencijabilnih.
ajmo sada izračunati parcijalne derivacije.
[tex]\partial _kf(x_1,...,x_n)=\displaystyle\sum_{i=1, i\neq k}^{n}x_i[/tex]
sada ću pokazati zašto:
[tex]\displaystyle\sum_{1\leq i < j\leq n}x_ix_j=\displaystyle\sum _{i=1}^{n}x_i \displaystyle\sum _{j=i+1}^{n}x_j=\displaystyle\sum _{i=1}^{k}x_i\displaystyle\sum _{j=i+1}^{n}x_j + \displaystyle\sum _{i=k+1}^{n} x_i \displaystyle\sum _{j=i+1}^{n} x_j[/tex]
kada parcijalno deriviramo po [tex]x_k[/tex], ova druga suma biti će [tex]0[/tex] jer se [tex]x_k[/tex] u njoj uopće ne pojavljuje, a kada prvu malo raspišeš, vidjet ćeš da je ona jednaka [tex]x_1(x_2+...+x_k+...+x_n)+x_2(x_3+...+x_k+...+x_n)+...+x_k(x_{k+1}+...+x_n)[/tex] i kada to parcijalno deriviraš dobiješ upravo ovo što sam gore napisala.
dobro, ajmo sad izračunati [tex]Df(x)(x)[/tex].
budući da je funkcija realna djelovanje diferencijala na neki vektor ekvivalentno je skalarnom množenju gradijenta s tim vektorom.
dakle
[tex]Df(x)(x)=((\displaystyle\sum_{i=2}^{n}x_i, \displaystyle\sum_{i=1, i\neq 2}^{n}x_i,..., \displaystyle\sum_{i=1}^{n-1}x_i)|(x_1,..., x_n))=\displaystyle\sum_{j=1}^{n}x_j\displaystyle\sum_{i=1, i\neq j}^{n}x_i = \displaystyle\sum_{j=1}^{n}x_j\displaystyle\sum_{i=1}^{j-1}x_i + \displaystyle\sum_{j=1}^{n}x_j\displaystyle\sum_{i=j+1}^{n}x_i=\displaystyle\sum_{1\leq i<j \leq n}x_ix_j + \displaystyle\sum_{1\leq j<i \leq n}x_ix_j[/tex]
zamjenom indeksa u drugoj sumi dobivamo da je to upravo
[tex]\displaystyle2\sum_{1\leq i<j \leq n}x_ix_j[/tex]
EDIT: aha zaboravila sam napisati što je diferencijal, odnosno njegov matrični prikaz. pa to je [tex]1\times n[/tex] matrica s koordinatama [tex]\partial _kf[/tex]. vidi gradijent  |
mislim da ti nije dobro jer index i ti mora biti manji od j
ja sam dobila ovako za diferencijal:
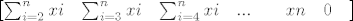
Added after 1 minutes:
ja sam za pokazati diferencijabilnost išla to pomoću definicije. Jeli okej samo ovako komentirati zašto je funkcija dfb(vidi se) ili se mora pomoću def? jer piše "pokažite da je fun dfb..."
|
|
| [Vrh] |
|
Loo
Forumaš(ica)


Pridružen/a: 11. 06. 2012. (16:02:07)
Postovi: (D0)16
Spol: 
|
 Postano: 11:12 sub, 22. 12. 2012 Naslov: Postano: 11:12 sub, 22. 12. 2012 Naslov: |
    |
|
|
raspiši si sumu, [tex]x_k[/tex] će ti se pojaviti kada je [tex]i=k[/tex] i biti će pomnožen sa svim [tex]x_j[/tex] za koje je [tex]j>k[/tex], ali pojavit će se i kada je [tex]j=k[/tex] i biti će pomnožen sa svim [tex]x_i[/tex] za koje je [tex]i<k[/tex]
uzmi npr. [tex]k=3[/tex].
pojavit će se [tex]x_1x_3, x_2x_3[/tex] za [tex]i=1, 2, j=3[/tex], ali i [tex]x_3x_4, x_3x_5,...,x_3x_n[/tex] za [tex]i=3[/tex]
kada deriviraš po [tex]x_3[/tex] dobiješ [tex]x_1+x_2+x_4+x_5+...+x_n[/tex] što je različito od ovog što si ti napisala
raspiši si sumu, [tex]x_k[/tex] će ti se pojaviti kada je [tex]i=k[/tex] i biti će pomnožen sa svim [tex]x_j[/tex] za koje je [tex]j>k[/tex], ali pojavit će se i kada je [tex]j=k[/tex] i biti će pomnožen sa svim [tex]x_i[/tex] za koje je [tex]i<k[/tex]
uzmi npr. [tex]k=3[/tex].
pojavit će se [tex]x_1x_3, x_2x_3[/tex] za [tex]i=1, 2, j=3[/tex], ali i [tex]x_3x_4, x_3x_5,...,x_3x_n[/tex] za [tex]i=3[/tex]
kada deriviraš po [tex]x_3[/tex] dobiješ [tex]x_1+x_2+x_4+x_5+...+x_n[/tex] što je različito od ovog što si ti napisala
|
|
| [Vrh] |
|
R2-D2
Forumaš(ica)

Pridružen/a: 11. 10. 2011. (20:32:10)
Postovi: (2F)16
|
 Postano: 13:17 sub, 22. 12. 2012 Naslov: Postano: 13:17 sub, 22. 12. 2012 Naslov: |
    |
|
|
[quote]može pomoć s limesom za točke oblika (0,y) y iz R [/quote]
okej, [tex] \dfrac{\partial f}{\partial x}(0,y) = \displaystyle \lim_{h\to 0}\dfrac{f(h,y) - f(0,y)}{h} = \displaystyle \lim_{h\to 0}\dfrac{ln(1+h^2y^2)}{h^2} = y^2 [/tex](primijenila sam L'Hospitalovo pravilo), i [tex] \dfrac{\partial f}{\partial y}(0,y) = \displaystyle \lim_{h\to 0}\dfrac{f(0,y+h) - f(0,y)}{h} = \displaystyle \lim_{h\to 0}\dfrac{0}{h} = 0 [/tex].
Sad trebamo pokazati da je [tex] \displaystyle \lim_{(x,y)\to (0,y_0)}\dfrac{\partial f}{\partial x }(x,y) = \dfrac{\partial f}{\partial x}(0,y_0)[/tex].
[tex] \displaystyle \lim_{(x,y)\to (0,y_0)}\dfrac{\partial f}{\partial x }(x,y) = \displaystyle \lim_{(x,y)\to (0,y_0)}\dfrac{2y^2}{1+x^2y^2 } - \dfrac{ln(1+x^2y^2)}{x^2}[/tex]
Limes prvog člana je očito [tex]2y_0^2[/tex], dok je [tex] \displaystyle \lim_{(x,y)\to (0,y_0)}\dfrac{ln(1+x^2y^2)}{x^2} = \displaystyle \lim_{(x,y)\to (0,y_0)}\dfrac{y^2ln(1+x^2y^2)}{x^2y^2} = y_0^2 \displaystyle \lim_{(x,y)\to (0,y_0)}\dfrac{ln(1+x^2y^2)}{x^2y^2} = [t=x^2y^2] = y_0^2\displaystyle \lim_{t\to 0}\dfrac{ln(1+t)}{t} = y_0^2.[/tex] Dakle, [tex] \displaystyle \lim_{(x,y)\to (0,y_0)}\dfrac{\partial f}{\partial x }(x,y) = y_0^2 = \dfrac{\partial f}{\partial x}(0,y_0)[/tex].
Neprekidnost parcijalne derivacije po y se lako pokaže.
| Citat: | | može pomoć s limesom za točke oblika (0,y) y iz R |
okej, [tex] \dfrac{\partial f}{\partial x}(0,y) = \displaystyle \lim_{h\to 0}\dfrac{f(h,y) - f(0,y)}{h} = \displaystyle \lim_{h\to 0}\dfrac{ln(1+h^2y^2)}{h^2} = y^2 [/tex](primijenila sam L'Hospitalovo pravilo), i [tex] \dfrac{\partial f}{\partial y}(0,y) = \displaystyle \lim_{h\to 0}\dfrac{f(0,y+h) - f(0,y)}{h} = \displaystyle \lim_{h\to 0}\dfrac{0}{h} = 0 [/tex].
Sad trebamo pokazati da je [tex] \displaystyle \lim_{(x,y)\to (0,y_0)}\dfrac{\partial f}{\partial x }(x,y) = \dfrac{\partial f}{\partial x}(0,y_0)[/tex].
[tex] \displaystyle \lim_{(x,y)\to (0,y_0)}\dfrac{\partial f}{\partial x }(x,y) = \displaystyle \lim_{(x,y)\to (0,y_0)}\dfrac{2y^2}{1+x^2y^2 } - \dfrac{ln(1+x^2y^2)}{x^2}[/tex]
Limes prvog člana je očito [tex]2y_0^2[/tex], dok je [tex] \displaystyle \lim_{(x,y)\to (0,y_0)}\dfrac{ln(1+x^2y^2)}{x^2} = \displaystyle \lim_{(x,y)\to (0,y_0)}\dfrac{y^2ln(1+x^2y^2)}{x^2y^2} = y_0^2 \displaystyle \lim_{(x,y)\to (0,y_0)}\dfrac{ln(1+x^2y^2)}{x^2y^2} = [t=x^2y^2] = y_0^2\displaystyle \lim_{t\to 0}\dfrac{ln(1+t)}{t} = y_0^2.[/tex] Dakle, [tex] \displaystyle \lim_{(x,y)\to (0,y_0)}\dfrac{\partial f}{\partial x }(x,y) = y_0^2 = \dfrac{\partial f}{\partial x}(0,y_0)[/tex].
Neprekidnost parcijalne derivacije po y se lako pokaže.
|
|
| [Vrh] |
|
pedro
Forumaš(ica)

Pridružen/a: 21. 10. 2010. (14:08:21)
Postovi: (19B)16
|
 Postano: 23:53 sub, 22. 12. 2012 Naslov: Postano: 23:53 sub, 22. 12. 2012 Naslov: |
    |
|
|
[quote="Loo"]raspiši si sumu, [tex]x_k[/tex] će ti se pojaviti kada je [tex]i=k[/tex] i biti će pomnožen sa svim [tex]x_j[/tex] za koje je [tex]j>k[/tex], ali pojavit će se i kada je [tex]j=k[/tex] i biti će pomnožen sa svim [tex]x_i[/tex] za koje je [tex]i<k[/tex]
uzmi npr. [tex]k=3[/tex].
pojavit će se [tex]x_1x_3, x_2x_3[/tex] za [tex]i=1, 2, j=3[/tex], ali i [tex]x_3x_4, x_3x_5,...,x_3x_n[/tex] za [tex]i=3[/tex]
kada deriviraš po [tex]x_3[/tex] dobiješ [tex]x_1+x_2+x_4+x_5+...+x_n[/tex] što je različito od ovog što si ti napisala[/quote]
ee hvalaa. :)
[size=9][color=#999999]Added after 2 minutes:[/color][/size]
[quote="R2-D2"][quote]može pomoć s limesom za točke oblika (0,y) y iz R [/quote]
okej, [tex] \dfrac{\partial f}{\partial x}(0,y) = \displaystyle \lim_{h\to 0}\dfrac{f(h,y) - f(0,y)}{h} = \displaystyle \lim_{h\to 0}\dfrac{ln(1+h^2y^2)}{h^2} = y^2 [/tex](primijenila sam L'Hospitalovo pravilo), i [tex] \dfrac{\partial f}{\partial y}(0,y) = \displaystyle \lim_{h\to 0}\dfrac{f(0,y+h) - f(0,y)}{h} = \displaystyle \lim_{h\to 0}\dfrac{0}{h} = 0 [/tex].
Sad trebamo pokazati da je [tex] \displaystyle \lim_{(x,y)\to (0,y_0)}\dfrac{\partial f}{\partial x }(x,y) = \dfrac{\partial f}{\partial x}(0,y_0)[/tex].
[tex] \displaystyle \lim_{(x,y)\to (0,y_0)}\dfrac{\partial f}{\partial x }(x,y) = \displaystyle \lim_{(x,y)\to (0,y_0)}\dfrac{2y^2}{1+x^2y^2 } - \dfrac{ln(1+x^2y^2)}{x^2}[/tex]
Limes prvog člana je očito [tex]2y_0^2[/tex], dok je [tex] \displaystyle \lim_{(x,y)\to (0,y_0)}\dfrac{ln(1+x^2y^2)}{x^2} = \displaystyle \lim_{(x,y)\to (0,y_0)}\dfrac{y^2ln(1+x^2y^2)}{x^2y^2} = y_0^2 \displaystyle \lim_{(x,y)\to (0,y_0)}\dfrac{ln(1+x^2y^2)}{x^2y^2} = [t=x^2y^2] = y_0^2\displaystyle \lim_{t\to 0}\dfrac{ln(1+t)}{t} = y_0^2.[/tex] Dakle, [tex] \displaystyle \lim_{(x,y)\to (0,y_0)}\dfrac{\partial f}{\partial x }(x,y) = y_0^2 = \dfrac{\partial f}{\partial x}(0,y_0)[/tex].
Neprekidnost parcijalne derivacije po y se lako pokaže.[/quote]
ja sam išla pokazivat po definciji da je lim (h1,h2)->(0,y0) == 0
možeš tako rješit?
| Loo (napisa): | raspiši si sumu, [tex]x_k[/tex] će ti se pojaviti kada je [tex]i=k[/tex] i biti će pomnožen sa svim [tex]x_j[/tex] za koje je [tex]j>k[/tex], ali pojavit će se i kada je [tex]j=k[/tex] i biti će pomnožen sa svim [tex]x_i[/tex] za koje je [tex]i<k[/tex]
uzmi npr. [tex]k=3[/tex].
pojavit će se [tex]x_1x_3, x_2x_3[/tex] za [tex]i=1, 2, j=3[/tex], ali i [tex]x_3x_4, x_3x_5,...,x_3x_n[/tex] za [tex]i=3[/tex]
kada deriviraš po [tex]x_3[/tex] dobiješ [tex]x_1+x_2+x_4+x_5+...+x_n[/tex] što je različito od ovog što si ti napisala |
ee hvalaa. 
Added after 2 minutes:
| R2-D2 (napisa): | | Citat: | | može pomoć s limesom za točke oblika (0,y) y iz R |
okej, [tex] \dfrac{\partial f}{\partial x}(0,y) = \displaystyle \lim_{h\to 0}\dfrac{f(h,y) - f(0,y)}{h} = \displaystyle \lim_{h\to 0}\dfrac{ln(1+h^2y^2)}{h^2} = y^2 [/tex](primijenila sam L'Hospitalovo pravilo), i [tex] \dfrac{\partial f}{\partial y}(0,y) = \displaystyle \lim_{h\to 0}\dfrac{f(0,y+h) - f(0,y)}{h} = \displaystyle \lim_{h\to 0}\dfrac{0}{h} = 0 [/tex].
Sad trebamo pokazati da je [tex] \displaystyle \lim_{(x,y)\to (0,y_0)}\dfrac{\partial f}{\partial x }(x,y) = \dfrac{\partial f}{\partial x}(0,y_0)[/tex].
[tex] \displaystyle \lim_{(x,y)\to (0,y_0)}\dfrac{\partial f}{\partial x }(x,y) = \displaystyle \lim_{(x,y)\to (0,y_0)}\dfrac{2y^2}{1+x^2y^2 } - \dfrac{ln(1+x^2y^2)}{x^2}[/tex]
Limes prvog člana je očito [tex]2y_0^2[/tex], dok je [tex] \displaystyle \lim_{(x,y)\to (0,y_0)}\dfrac{ln(1+x^2y^2)}{x^2} = \displaystyle \lim_{(x,y)\to (0,y_0)}\dfrac{y^2ln(1+x^2y^2)}{x^2y^2} = y_0^2 \displaystyle \lim_{(x,y)\to (0,y_0)}\dfrac{ln(1+x^2y^2)}{x^2y^2} = [t=x^2y^2] = y_0^2\displaystyle \lim_{t\to 0}\dfrac{ln(1+t)}{t} = y_0^2.[/tex] Dakle, [tex] \displaystyle \lim_{(x,y)\to (0,y_0)}\dfrac{\partial f}{\partial x }(x,y) = y_0^2 = \dfrac{\partial f}{\partial x}(0,y_0)[/tex].
Neprekidnost parcijalne derivacije po y se lako pokaže. |
ja sam išla pokazivat po definciji da je lim (h1,h2)→(0,y0) == 0
možeš tako rješit?
|
|
| [Vrh] |
|
R2-D2
Forumaš(ica)


Pridružen/a: 11. 10. 2011. (20:32:10)
Postovi: (2F)16
|
 Postano: 0:51 ned, 23. 12. 2012 Naslov: Postano: 0:51 ned, 23. 12. 2012 Naslov: |
    |
|
|
okej, iz parcijalnih derivacija dobili smo da je kandidat za operator [tex]\begin{pmatrix}
y_0^2 & 0
\end{pmatrix} [/tex]
Sad imamo [tex] | \dfrac{f(x,y) - f(0,y_0) - y_0^2 \cdot x}{\sqrt{x^2 + (y-y_0)^2}}| \le | \dfrac{ f(x,y) - y_0^2 \cdot x}{\sqrt{x^2}}| = | \dfrac{f(x,y) - y_0^2 \cdot x}{x}| = | \dfrac{ln(1+x^2y^2)}{x^2} - y_0^2| [/tex]
Sad ako pustimo [tex](x,y) \to (0,y_0) [/tex] na jednak način kao kod neprekidnosti parcijalne derivacije po x dobijemo da je limes prvog člana [tex]y_0^2 [/tex] pa po teoremu o sendviču slijedi da je cijeli limes 0. Ali, budući da se u zadatku traži da pokažemo da je funkcija klase [tex]C^1[/tex], onda opet trebamo pokazati neprekidnost parcijalnih derivacija.
okej, iz parcijalnih derivacija dobili smo da je kandidat za operator [tex]\begin{pmatrix}
y_0^2 & 0
\end{pmatrix} [/tex]
Sad imamo [tex] | \dfrac{f(x,y) - f(0,y_0) - y_0^2 \cdot x}{\sqrt{x^2 + (y-y_0)^2}}| \le | \dfrac{ f(x,y) - y_0^2 \cdot x}{\sqrt{x^2}}| = | \dfrac{f(x,y) - y_0^2 \cdot x}{x}| = | \dfrac{ln(1+x^2y^2)}{x^2} - y_0^2| [/tex]
Sad ako pustimo [tex](x,y) \to (0,y_0) [/tex] na jednak način kao kod neprekidnosti parcijalne derivacije po x dobijemo da je limes prvog člana [tex]y_0^2 [/tex] pa po teoremu o sendviču slijedi da je cijeli limes 0. Ali, budući da se u zadatku traži da pokažemo da je funkcija klase [tex]C^1[/tex], onda opet trebamo pokazati neprekidnost parcijalnih derivacija.
|
|
| [Vrh] |
|
angelika
Forumaš(ica)

Pridružen/a: 08. 02. 2011. (17:26:51)
Postovi: (5F)16
|
|
| [Vrh] |
|
Phoenix
Forumaš(ica)


Pridružen/a: 15. 05. 2010. (18:46:07)
Postovi: (164)16
Sarma: -
|
 Postano: 19:56 sri, 26. 12. 2012 Naslov: Postano: 19:56 sri, 26. 12. 2012 Naslov: |
    |
|
|
Ako je [tex](x,y)[/tex] ekstrem od [tex]f[/tex] (na elipsi), tada za [tex]g:\mathbb{R}^2 \rightarrow \mathbb{R}, g(x,y)=\frac{x^2}{2}+y^2-1[/tex] postoji [tex]\lambda \in \mathbb{R}[/tex] takav da vrijedi [tex]\nabla f(x,y)=\lambda \nabla g(x,y)[/tex].
To je ono što kaže teorem. A sada dalje imamo [tex](3x-2,-2y)=\lambda (x,2y)[/tex], odnosno sustav [tex]3x-2=\lambda x, -2y= \lambda \cdot 2y[/tex].
Iz druge jednadžbe slijedi [tex]\lambda = -1[/tex] ili [tex]y=0[/tex].
Za [tex]\lambda = -1[/tex] iz prve jednadžbe imamo [tex]3x-2=-x[/tex], odnosno [tex]x=\frac{1}{2}[/tex]. Sada se treba prisjetiti da vrijedi [tex]g(x,y)=0[/tex] pa iz toga dobivamo [tex]y=\pm \frac{\sqrt{14}}{4}[/tex]. Dakle, prvi kandidati za ekstrem su [tex](\frac{1}{2},\pm \frac{\sqrt{14}}{4})[/tex].
Preostaje slučaj [tex]y=0[/tex]. Iz uvjeta [tex]g(x,y)=0[/tex] dobivamo [tex]x=\pm \sqrt{2}[/tex], stoga su druga dva kandidata [tex](\pm \sqrt{2},0)[/tex].
Sada računamo koliko je [tex]f(x,y)[/tex] za sva četiri kandidata. Dobivamo:
[tex]f(\frac{1}{2},\pm \frac{\sqrt{14}}{4})=\frac{3}{2} \cdot \frac{1}{4}-2 \cdot \frac{1}{2}-(\pm \frac{\sqrt{14}}{4})^2=\frac{3}{4}-1-\frac{7}{8}=-\frac{9}{8}[/tex]
[tex]f(\sqrt{2},0)=\frac{3}{2}\cdot 2-2\sqrt{2}-0^2=3-2\sqrt{2}[/tex]
[tex]f(-\sqrt{2},0)=\frac{3}{2}\cdot 2-2(-\sqrt{2})-0^2=3+2\sqrt{2}[/tex]
Konačno, globalni minimum se postiže u točkama [tex](\frac{1}{2},\pm \frac{\sqrt{14}}{4})[/tex], a globalni maksimum u točki [tex](-\sqrt{2},0)[/tex].
Ako je [tex](x,y)[/tex] ekstrem od [tex]f[/tex] (na elipsi), tada za [tex]g:\mathbb{R}^2 \rightarrow \mathbb{R}, g(x,y)=\frac{x^2}{2}+y^2-1[/tex] postoji [tex]\lambda \in \mathbb{R}[/tex] takav da vrijedi [tex]\nabla f(x,y)=\lambda \nabla g(x,y)[/tex].
To je ono što kaže teorem. A sada dalje imamo [tex](3x-2,-2y)=\lambda (x,2y)[/tex], odnosno sustav [tex]3x-2=\lambda x, -2y= \lambda \cdot 2y[/tex].
Iz druge jednadžbe slijedi [tex]\lambda = -1[/tex] ili [tex]y=0[/tex].
Za [tex]\lambda = -1[/tex] iz prve jednadžbe imamo [tex]3x-2=-x[/tex], odnosno [tex]x=\frac{1}{2}[/tex]. Sada se treba prisjetiti da vrijedi [tex]g(x,y)=0[/tex] pa iz toga dobivamo [tex]y=\pm \frac{\sqrt{14}}{4}[/tex]. Dakle, prvi kandidati za ekstrem su [tex](\frac{1}{2},\pm \frac{\sqrt{14}}{4})[/tex].
Preostaje slučaj [tex]y=0[/tex]. Iz uvjeta [tex]g(x,y)=0[/tex] dobivamo [tex]x=\pm \sqrt{2}[/tex], stoga su druga dva kandidata [tex](\pm \sqrt{2},0)[/tex].
Sada računamo koliko je [tex]f(x,y)[/tex] za sva četiri kandidata. Dobivamo:
[tex]f(\frac{1}{2},\pm \frac{\sqrt{14}}{4})=\frac{3}{2} \cdot \frac{1}{4}-2 \cdot \frac{1}{2}-(\pm \frac{\sqrt{14}}{4})^2=\frac{3}{4}-1-\frac{7}{8}=-\frac{9}{8}[/tex]
[tex]f(\sqrt{2},0)=\frac{3}{2}\cdot 2-2\sqrt{2}-0^2=3-2\sqrt{2}[/tex]
[tex]f(-\sqrt{2},0)=\frac{3}{2}\cdot 2-2(-\sqrt{2})-0^2=3+2\sqrt{2}[/tex]
Konačno, globalni minimum se postiže u točkama [tex](\frac{1}{2},\pm \frac{\sqrt{14}}{4})[/tex], a globalni maksimum u točki [tex](-\sqrt{2},0)[/tex].
|
|
| [Vrh] |
|
|






