| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
smajl
Forumaš(ica)

Pridružen/a: 02. 01. 2010. (12:59:23)
Postovi: (EB)16
Spol: 
Lokacija: Zagreb
|
|
| [Vrh] |
|
holidayRainbowLights
Forumaš(ica)


Pridružen/a: 28. 03. 2012. (23:58:54)
Postovi: (11)16
Spol: 
|
|
| [Vrh] |
|
minora665
Forumaš(ica)

Pridružen/a: 10. 02. 2010. (22:52:01)
Postovi: (1F)16
|
|
| [Vrh] |
|
holidayRainbowLights
Forumaš(ica)


Pridružen/a: 28. 03. 2012. (23:58:54)
Postovi: (11)16
Spol: 
|
|
| [Vrh] |
|
minora665
Forumaš(ica)

Pridružen/a: 10. 02. 2010. (22:52:01)
Postovi: (1F)16
|
|
| [Vrh] |
|
frutabella
Forumaš(ica)

Pridružen/a: 09. 10. 2010. (16:35:36)
Postovi: (24E)16
|
|
| [Vrh] |
|
hendrix
Forumaš(ica)

Pridružen/a: 03. 09. 2012. (15:59:06)
Postovi: (92)16
|
|
| [Vrh] |
|
frutabella
Forumaš(ica)

Pridružen/a: 09. 10. 2010. (16:35:36)
Postovi: (24E)16
|
|
| [Vrh] |
|
dodinho
Forumaš(ica)
Pridružen/a: 27. 09. 2011. (11:17:47)
Postovi: (4B)16
|
|
| [Vrh] |
|
@na
Forumaš(ica)

Pridružen/a: 16. 10. 2011. (13:29:26)
Postovi: (14)16
Spol: 
|
|
| [Vrh] |
|
dodinho
Forumaš(ica)
Pridružen/a: 27. 09. 2011. (11:17:47)
Postovi: (4B)16
|
|
| [Vrh] |
|
Megy Poe
Forumaš(ica)

Pridružen/a: 05. 11. 2009. (23:14:52)
Postovi: (122)16
|
|
| [Vrh] |
|
dodinho
Forumaš(ica)
Pridružen/a: 27. 09. 2011. (11:17:47)
Postovi: (4B)16
|
 Postano: 21:19 sub, 29. 12. 2012 Naslov: Postano: 21:19 sub, 29. 12. 2012 Naslov: |
    |
|
|
Na zadnjem predavanju smo odradili ono cca. 15 stranica, sto na preskake, sto na raspisivanje(manje :wink: ). Uglavnom, odradili smo do kraja ordinalne br., prosli kardinalne br. te nakon toga i aksiom izbora. Mislim, do 93/94 stranice iz skripte
[size=9][color=#999999]Added after 12 minutes:[/color][/size]
S time da je prof. rekao da ce neke teoreme pitat samo iskaz, jer nije stigao dokazat. To se vjerojatno odnosi i na usmeni, ali nisam ziher. Neke koje sam zapisao : Burali-Fortijev paradoks, Tm 2.28 Transfinitna indukcija, Teorem rekurzije, definicija 2.51...ono sto ce sigurno pitat je Teorem enumeracije, ZORNOVA LEMA, to je posebno naglasio. Nek me netko ispravi ako zna bolje. I naravno, svaka inf je dobro dosla 8)
Na zadnjem predavanju smo odradili ono cca. 15 stranica, sto na preskake, sto na raspisivanje(manje  ). Uglavnom, odradili smo do kraja ordinalne br., prosli kardinalne br. te nakon toga i aksiom izbora. Mislim, do 93/94 stranice iz skripte ). Uglavnom, odradili smo do kraja ordinalne br., prosli kardinalne br. te nakon toga i aksiom izbora. Mislim, do 93/94 stranice iz skripte
Added after 12 minutes:
S time da je prof. rekao da ce neke teoreme pitat samo iskaz, jer nije stigao dokazat. To se vjerojatno odnosi i na usmeni, ali nisam ziher. Neke koje sam zapisao : Burali-Fortijev paradoks, Tm 2.28 Transfinitna indukcija, Teorem rekurzije, definicija 2.51...ono sto ce sigurno pitat je Teorem enumeracije, ZORNOVA LEMA, to je posebno naglasio. Nek me netko ispravi ako zna bolje. I naravno, svaka inf je dobro dosla 
|
|
| [Vrh] |
|
Sphiro
Forumaš(ica)
Pridružen/a: 17. 10. 2007. (16:32:45)
Postovi: (45)16
|
|
| [Vrh] |
|
dodinho
Forumaš(ica)
Pridružen/a: 27. 09. 2011. (11:17:47)
Postovi: (4B)16
|
|
| [Vrh] |
|
pupi
Forumaš(ica)

Pridružen/a: 20. 12. 2009. (11:03:15)
Postovi: (92)16
Spol: 
|
|
| [Vrh] |
|
ceps
Forumaš(ica)

Pridružen/a: 08. 10. 2010. (13:03:07)
Postovi: (13A)16
|
|
| [Vrh] |
|
pupi
Forumaš(ica)

Pridružen/a: 20. 12. 2009. (11:03:15)
Postovi: (92)16
Spol: 
|
|
| [Vrh] |
|
kikzmyster
Forumaš(ica)

Pridružen/a: 14. 10. 2010. (13:35:08)
Postovi: (72)16
Spol: 
|
 Postano: 3:01 sri, 9. 1. 2013 Naslov: Postano: 3:01 sri, 9. 1. 2013 Naslov: |
    |
|
|
[latex]\mathbb{R} \times \mathbb{R} [/latex] nema prebrojiv, gust podskup (sto je invarijanta slicnosti, a [latex]\mathbb{R} [/latex] ima takav podskup). Naime, neka je [latex]A \subseteq \mathbb{R}\times \mathbb{R}[/latex] gust podskup. Onda za svaki [latex]x \in \mathbb{R}[/latex] postoji [latex]a_x \in A[/latex] takav da je [latex] (0,x) < a_x < (1, x) [/latex]. Ovi [latex]a_x[/latex] su medusobno razliciti, a ima ih neprebrojivo mnogo, dakle [latex]A[/latex] je neprebrojiv skup. Znaci, [latex]\mathbb{R} \times \mathbb{R} [/latex] nema prebrojiv gust podskup.
EDIT: Sori ceps, nisam vidio da je ovo pitanje u biti hint za rjesavanje zadatka, ali eto, neka bude tu kao uputa za pupi :D
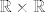 nema prebrojiv, gust podskup (sto je invarijanta slicnosti, a nema prebrojiv, gust podskup (sto je invarijanta slicnosti, a 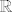 ima takav podskup). Naime, neka je ima takav podskup). Naime, neka je 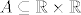 gust podskup. Onda za svaki gust podskup. Onda za svaki 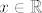 postoji postoji 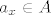 takav da je takav da je 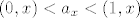 . Ovi . Ovi 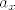 su medusobno razliciti, a ima ih neprebrojivo mnogo, dakle su medusobno razliciti, a ima ih neprebrojivo mnogo, dakle  je neprebrojiv skup. Znaci, je neprebrojiv skup. Znaci, 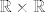 nema prebrojiv gust podskup. nema prebrojiv gust podskup.
EDIT: Sori ceps, nisam vidio da je ovo pitanje u biti hint za rjesavanje zadatka, ali eto, neka bude tu kao uputa za pupi 
|
|
| [Vrh] |
|
pupi
Forumaš(ica)

Pridružen/a: 20. 12. 2009. (11:03:15)
Postovi: (92)16
Spol: 
|
|
| [Vrh] |
|
|












