| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
Gost
|
 Postano: 16:42 uto, 17. 8. 2004 Naslov: Kriterij integrabilnosti |
    |
|
|
[color=green]Teorem(Kriterij integrabilnosti) :
Neka je f : [a,b] -> IR omeđena.Tada je ona (R)-integrabilna ako i samo ako za svaki eps>0 postoji subdivizija d=d(eps) segmenta [a,b] takva da je:
S(d)-s(d)<eps[/color]
[color=darkblue]( S(d) i s(d) su gornja i donja Darbuova suma)[/color]
Dokaz:
Nužnost(=>) :
Eps>0 proizvoljan
Promotrimo broj I* + eps/2 I*=inf B
[color=darkblue](Broj I* je gornji Reimanov integral odnosno infimum svih gornjih Darbuovih suma,a skup B je skup svih gornjih Darbuovih suma)[/color]
=> postoji d1 takva da I*<=S(d1)<I*+eps/2 [color=darkblue](to slijedi iz definicije infimuma)[/color]
Promotrimo i broj I-eps/2 , I=supA
[color=darkblue](Broj I je donji Reimanov integral odnosno supremum svih donjih Darbuovih suma,a skup A je skup svih donjih Darbuovih suma)[/color]
=>postoji d2 takva da I-eps/2<s(d2)<=I [color=darkblue](to slijedi iz definicije supremuma)[/color]
d=d1Ud2
I-eps/2<s(d2)<=s(d)<=S(d)<=S(d1)<I*+eps/2
=> S(d)-s(d)<=I*+eps/2-(I-eps/2)=eps
=>S(d)-s(d)<=eps
[color=darkblue]Moje pitanje:
Pa tvrdnja teorema kaže da mora vrijediti S(d)-s(d)<eps ,otkud onda S(d)-s(d)<=eps ?[/color]
Dovoljnost(<=) :
Eps>0 proizvoljan
Kriterij => postoji d takva da S(d)-s(d)<eps
s(d)<=I<=I*<=S(d)
=> I*-I<=S(d)-s(d)<eps za svaki eps>0 => I*-I=0 tj I*=I
Teorem(Kriterij integrabilnosti) :
Neka je f : [a,b] → IR omeđena.Tada je ona (R)-integrabilna ako i samo ako za svaki eps>0 postoji subdivizija d=d(eps) segmenta [a,b] takva da je:
S(d)-s(d)<eps
( S(d) i s(d) su gornja i donja Darbuova suma)
Dokaz:
Nužnost(⇒) :
Eps>0 proizvoljan
Promotrimo broj I* + eps/2 I*=inf B
(Broj I* je gornji Reimanov integral odnosno infimum svih gornjih Darbuovih suma,a skup B je skup svih gornjih Darbuovih suma)
⇒ postoji d1 takva da I*⇐S(d1)<I*+eps/2 (to slijedi iz definicije infimuma)
Promotrimo i broj I-eps/2 , I=supA
(Broj I je donji Reimanov integral odnosno supremum svih donjih Darbuovih suma,a skup A je skup svih donjih Darbuovih suma)
⇒postoji d2 takva da I-eps/2<s(d2)⇐I (to slijedi iz definicije supremuma)
d=d1Ud2
I-eps/2<s(d2)⇐s(d)⇐S(d)⇐S(d1)<I*+eps/2
⇒ S(d)-s(d)⇐I*+eps/2-(I-eps/2)=eps
⇒S(d)-s(d)⇐eps
Moje pitanje:
Pa tvrdnja teorema kaže da mora vrijediti S(d)-s(d)<eps ,otkud onda S(d)-s(d)⇐eps ?
Dovoljnost(⇐) :
Eps>0 proizvoljan
Kriterij ⇒ postoji d takva da S(d)-s(d)<eps
s(d)⇐I⇐I*⇐S(d)
⇒ I*-I⇐S(d)-s(d)<eps za svaki eps>0 ⇒ I*-I=0 tj I*=I
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
ZELENIZUBNAPLANETIDO
SADE
Forumaš(ica)
Pridružen/a: 04. 03. 2004. (19:56:15)
Postovi: (54F)16
Lokacija: hm?
|
| Postano: 10:09 sri, 18. 8. 2004 Naslov: Re: Kriterij integrabilnosti |
|
|
|
[quote="Anonymous"][color=green]Teorem(Kriterij integrabilnosti) :
Neka je f : [a,b] -> IR omeđena.Tada je ona (R)-integrabilna ako i samo ako za svaki eps>0 postoji subdivizija d=d(eps) segmenta [a,b] takva da je:
S(d)-s(d)<eps[/color][/quote]
Definiramo gornji i donji (R)-integral:
[latex]I^* := \inf\{S(\delta)=D(f,\delta):\delta \in \Delta\}[/latex]
[latex]I_*:=\sup\{s(\delta)=d(f,\delta):\delta \in \Delta\}[/latex]
I tvrdimo:
[latex]~I^*=I_* ~\Longleftrightarrow (\forall \varepsilon>0) (\exists \delta \in \Delta)~ t.d. ~ S(\delta)-s(\delta)<\varepsilon[/latex]
Nuznost:
[latex]I^*=I_* \Longrightarrow \left .\begin{array}{l}\forall (\varepsilon>0) (\delta_1 \in \Delta)~ t.d. ~S(\delta)-I^* \leq \frac{\varepsilon}{2} \\ \forall (\varepsilon>0) (\delta_2 \in \Delta)~ t.d. ~I_*-s(\delta) \leq \frac{\varepsilon}{2} \end{array} \right \}+ \Longrightarrow[/latex]
[quote="Anonymous"]Moje pitanje:
Pa tvrdnja teorema kaže da mora vrijediti S(d)-s(d)<eps ,otkud onda S(d)-s(d)<=eps ?[/quote]
<= dolazi iz nacina na koji smo definirali supremum, no, dosta je jasno da ako tvrdnja vrijedi za <= da vrijedi i za strogo <. To mozemo postici, npr. mnozenjem desne strane sa 2 :), tj.
[latex]\delta:=\delta_1 \cup \delta_2\\
(\forall \varepsilon>0) (\exists \delta \in \Delta)~ t.d. ~S(\delta)-s(\delta)+I^*-I_*=^{~zbog pocetnog uvijeta~}[/latex]
[latex]S(\delta)-s(\delta) \leq \varepsilon <2\varepsilon[/latex] :)
[quote="Anonymous"]_moja_(pa samo provjerite jesam li u pravu) interpretacija:
ako je funkcija omeđena najveća donja Darbuova suma je ili jednaka najvećoj gornjoj Darbuovoj sumi(u tom slučaju imamo integrabilnost) ili manja(nemamo integrabilnosti).[/quote]
Cinjenica da postoji supremum donje darbouxove sume, ne znaci da postoji i "najveca donja darbouxova suma" :!: analogno i za gornje D. sume
[quote="Anonymous"]U svakom slučaju najveća donja D.suma nikada ne može biti veća od najmanje gornje.[/quote]
Nikada je ipak malo pre jaka rijec ;) :) Uzmi primjer konstantne fje - sve gornje i donje darbouxove sume su jednake gornjem, tj. i donjem (R)-integralu.
Drugi smijer:
[latex](\forall \varepsilon>0) (\exists \delta \in \Delta)~ t.d. ~ S(\delta)-s(\delta)<\varepsilon \Longrightarrow[/latex]
[quote="Anonymous"]Dakle I<=I* => I*-I>=0 kako onda u dokazu zaključujemo :[
za svaki eps>0 => I*-I=0[/quote]
Zbog slijedece relacije koju ste, vjerujem dokazali negdje ranije:
[latex]s(\delta)<=I_*<=I^*<=S(\delta)[/latex]
tj, drugim rijecima, "udaljenost" izmedju gornje i donje darbouxove sume je manja ili jednaka "udaljenosti" izmedju gornjeg i donjeg (R)-integrala i zato zakljucujemo:
[latex]0 \leq I^*-I_* \leq S(\delta)-s(\delta)<\varepsilon \Longrightarrow I^*=I_*[/latex]
tj. [latex]I^* - I_* < \varepsilon~ ~ \forall \varepsilon>0[/latex]
...a buduci da je razlika gornjeg i donjeg (R)-integrala konkretan, invarijantan broj koji je manji od svakog broja veceg od 0, onda ta razlika ne moze biti nista drugo nego 0 :)
PS pise se "Darboux" ;)
PPS ako pokusas kvoutat formule, neces uspijeti dok god se ne logiras kao registrirani korisnik. Ako imas problema sa registracijom (buduci da se jos uvijek nisi registrirao :-k), posalji vsegi mail
| Anonymous (napisa): | Teorem(Kriterij integrabilnosti) :
Neka je f : [a,b] → IR omeđena.Tada je ona (R)-integrabilna ako i samo ako za svaki eps>0 postoji subdivizija d=d(eps) segmenta [a,b] takva da je:
S(d)-s(d)<eps |
Definiramo gornji i donji (R)-integral:
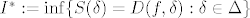
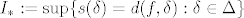
I tvrdimo:
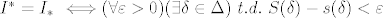
Nuznost:
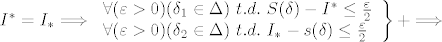
| Anonymous (napisa): | Moje pitanje:
Pa tvrdnja teorema kaže da mora vrijediti S(d)-s(d)<eps ,otkud onda S(d)-s(d)⇐eps ? |
⇐ dolazi iz nacina na koji smo definirali supremum, no, dosta je jasno da ako tvrdnja vrijedi za ⇐ da vrijedi i za strogo <. To mozemo postici, npr. mnozenjem desne strane sa 2  , tj.
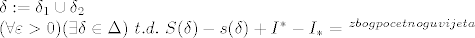
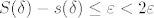
| Anonymous (napisa): | _moja_(pa samo provjerite jesam li u pravu) interpretacija:
ako je funkcija omeđena najveća donja Darbuova suma je ili jednaka najvećoj gornjoj Darbuovoj sumi(u tom slučaju imamo integrabilnost) ili manja(nemamo integrabilnosti). |
Cinjenica da postoji supremum donje darbouxove sume, ne znaci da postoji i "najveca donja darbouxova suma"  analogno i za gornje D. sume
| Anonymous (napisa): | | U svakom slučaju najveća donja D.suma nikada ne može biti veća od najmanje gornje. |
Nikada je ipak malo pre jaka rijec  Uzmi primjer konstantne fje - sve gornje i donje darbouxove sume su jednake gornjem, tj. i donjem (R)-integralu.
Drugi smijer:
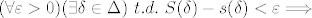
| Anonymous (napisa): | Dakle I⇐I* ⇒ I*-I>=0 kako onda u dokazu zaključujemo :[
za svaki eps>0 ⇒ I*-I=0 |
Zbog slijedece relacije koju ste, vjerujem dokazali negdje ranije:
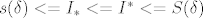
tj, drugim rijecima, "udaljenost" izmedju gornje i donje darbouxove sume je manja ili jednaka "udaljenosti" izmedju gornjeg i donjeg (R)-integrala i zato zakljucujemo:
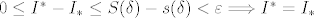
tj.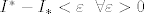 
...a buduci da je razlika gornjeg i donjeg (R)-integrala konkretan, invarijantan broj koji je manji od svakog broja veceg od 0, onda ta razlika ne moze biti nista drugo nego 0
PS pise se "Darboux"
PPS ako pokusas kvoutat formule, neces uspijeti dok god se ne logiras kao registrirani korisnik. Ako imas problema sa registracijom (buduci da se jos uvijek nisi registrirao  ), posalji vsegi mail
_________________ 
Pupoljak nije negiran. Rekao sam to i ponovit cu to jos jedanput. Pupoljak NIJE negirAn.
MADD
(Mothers Against Dirty Dialectics)
Based on a true story. NOT.
Ko ih sljivi, mi sviramo punk |
|
| [Vrh] |
|
Gost
|
| Postano: 13:34 sri, 18. 8. 2004 Naslov: |
|
|
|
[quote]<= dolazi iz nacina na koji smo definirali supremum, no, dosta je jasno da ako tvrdnja vrijedi za <= da vrijedi i za strogo <. To mozemo postici, npr. mnozenjem desne strane sa 2 [/quote]
ma znaš kak si ja razmišljam?-uzeli smo proizvoljno strogo pozitivan broj eps i za njega kroz dokaz dobili nejednakost S(d)-s(d)<=eps,dakle,ta razlika suma može biti jednaka broju eps,a ja to ne smijem imati zbog kriterija koji zahtjeva strogu nejednakost.
Ti kažeš,množi taj broj eps sa 2 i imaš strogu nejednakost(slažem se),ali,nije li to ''lažiranje'' ?
Uzeo sam _eps proizvoljno_ i dobio score koji nisam htio,_nema lažiranja_(nije to Dinamo-Rijeka),za proizvoljan eps ja bih morao moći dobiti _strogu nejednakost_,a ja ju nisam dobio.
A opet(pazi sad ovo;)),svjestan sam činjenice da se svaki strogo pozitivan broj 'pepsi' može napisati u obliku : pepsi :=2*eps za eps>0 .
Daj mi sad pomogni u razmišljanju,gdje griješim ?
:o
Hajde da još rezimiram što tvrdi kriterij integrabilnosti:
Za svaki eps>0 … pa si ja zemem epsilon zdesna od nule dovoljno malen da potpuno određuje nulu,dakle da ga slobodno možemo proglasiti nulom(imavši u vidu,da on nikada nije apsolutna nula ali joj je dovoljno ''blizak'' da ga možemo takvim proglasiti,btw brojeva sa tim svojstvom oko nule ima neprebrojivo mnogo,brojevi u neposrednoj okolini slijeva od nule također potpuno određuju nulu pa se njima ''čak i uklanja minus'' ).
Kriterij je S(d)-s(d)<eps ,eps je mizerno veći od nule,dakle postoje takve Darboux-ove sume(donja i gornja) da vrijedi da je njihova razlika mizerna,naravno,te sume su I* i I.
Što te ja želim pitati ?
Dakle u definiciji Reiman integrabilnosti imamo jednakost I*=I ali ako ćemo biti ''Božje precizni'' to nije točno,jeli tako(sada sam to laički opisao),mislim ako ćemo biti ''B-O-Ž-J-E PRECIZNI''!
I naravno,sada je jasno zašto _'za svaki'_ epsilon to zahtjevamo jer,zapravo nas boli briga za sve ostale epsilone kada mi imamo potvrdu kriterija za eps koji aproksimira nulu,onda je logično da će vrijediti i za svaki veći strogo pozitivan broj ako već vrijedi za broj blizak nuli.
Reci da imam pravo.:o)
I što znači 'invarijantan broj' ?
[quote]PS pise se "Darboux" [/quote]
Ma mogao sam si misliti da će uspješan matematičar u prezimenu imati nepoznanicu x,cccc.
:o)
[quote]PPS ako pokusas kvoutat formule, neces uspijeti dok god se ne logiras kao registrirani korisnik. Ako imas problema sa registracijom (buduci da se jos uvijek nisi registrirao ), posalji vsegi mail[/quote]
ma prvo sam izgubio šifru,pa sam promijenio mail,pa sam rekao moderatoru da mi pošalje na novi mail pa je on rekao da mi ne vjeruje da sam ja ta osoba koja je imala izgubljenu šifru(što je logično jer nema dokaza;)) i tak me prošla volja za registriranjem…evo idem se regat na carnet,papirologiju sam sredio. 8)
| Citat: | | ⇐ dolazi iz nacina na koji smo definirali supremum, no, dosta je jasno da ako tvrdnja vrijedi za ⇐ da vrijedi i za strogo <. To mozemo postici, npr. mnozenjem desne strane sa 2 |
ma znaš kak si ja razmišljam?-uzeli smo proizvoljno strogo pozitivan broj eps i za njega kroz dokaz dobili nejednakost S(d)-s(d)⇐eps,dakle,ta razlika suma može biti jednaka broju eps,a ja to ne smijem imati zbog kriterija koji zahtjeva strogu nejednakost.
Ti kažeš,množi taj broj eps sa 2 i imaš strogu nejednakost(slažem se),ali,nije li to ''lažiranje'' ?
Uzeo sam _eps proizvoljno_ i dobio score koji nisam htio,_nema lažiranja_(nije to Dinamo-Rijeka),za proizvoljan eps ja bih morao moći dobiti _strogu nejednakost_,a ja ju nisam dobio.
A opet(pazi sad ovo;)),svjestan sam činjenice da se svaki strogo pozitivan broj 'pepsi' može napisati u obliku : pepsi :=2*eps za eps>0 .
Daj mi sad pomogni u razmišljanju,gdje griješim ?
Hajde da još rezimiram što tvrdi kriterij integrabilnosti:
Za svaki eps>0 … pa si ja zemem epsilon zdesna od nule dovoljno malen da potpuno određuje nulu,dakle da ga slobodno možemo proglasiti nulom(imavši u vidu,da on nikada nije apsolutna nula ali joj je dovoljno ''blizak'' da ga možemo takvim proglasiti,btw brojeva sa tim svojstvom oko nule ima neprebrojivo mnogo,brojevi u neposrednoj okolini slijeva od nule također potpuno određuju nulu pa se njima ''čak i uklanja minus'' ).
Kriterij je S(d)-s(d)<eps ,eps je mizerno veći od nule,dakle postoje takve Darboux-ove sume(donja i gornja) da vrijedi da je njihova razlika mizerna,naravno,te sume su I* i I.
Što te ja želim pitati ?
Dakle u definiciji Reiman integrabilnosti imamo jednakost I*=I ali ako ćemo biti ''Božje precizni'' to nije točno,jeli tako(sada sam to laički opisao),mislim ako ćemo biti ''B-O-Ž-J-E PRECIZNI''!
I naravno,sada je jasno zašto _'za svaki'_ epsilon to zahtjevamo jer,zapravo nas boli briga za sve ostale epsilone kada mi imamo potvrdu kriterija za eps koji aproksimira nulu,onda je logično da će vrijediti i za svaki veći strogo pozitivan broj ako već vrijedi za broj blizak nuli.
Reci da imam pravo.
I što znači 'invarijantan broj' ?
| Citat: | | PS pise se "Darboux" |
Ma mogao sam si misliti da će uspješan matematičar u prezimenu imati nepoznanicu x,cccc.
| Citat: | | PPS ako pokusas kvoutat formule, neces uspijeti dok god se ne logiras kao registrirani korisnik. Ako imas problema sa registracijom (buduci da se jos uvijek nisi registrirao ), posalji vsegi mail |
ma prvo sam izgubio šifru,pa sam promijenio mail,pa sam rekao moderatoru da mi pošalje na novi mail pa je on rekao da mi ne vjeruje da sam ja ta osoba koja je imala izgubljenu šifru(što je logično jer nema dokaza;)) i tak me prošla volja za registriranjem…evo idem se regat na carnet,papirologiju sam sredio. 
|
|
| [Vrh] |
|
mdoko
Forumaš(ica)
Pridružen/a: 30. 11. 2002. (22:17:12)
Postovi: (71A)16
Spol: 
Lokacija: Heriot-Watt University, Edinburgh
|
| Postano: 15:54 sri, 18. 8. 2004 Naslov: |
|
|
|
Prvo da rijesimo ono sa S(d)-s(d)<=eps
Evo ovako: dokazali smo da za svaki pozitivni broj eps mozemo pronaci subdiviziju d t.d. S(d)-s(d)<=eps.
OK, sada uzmimo proizvopljan e>0. Tada je i e/2 > 0. Po prethodno dokazanom postoji subdivizija d' t.d. S(d')-s(d')<=e/2[b]<[/b]e
Eto sada imamo strogu nejednakost.
[quote]
Za svaki eps>0 … pa si ja zemem epsilon zdesna od nule dovoljno malen da potpuno određuje nulu,dakle da ga slobodno možemo proglasiti nulom(imavši u vidu,da on nikada nije apsolutna nula ali joj je dovoljno ''blizak'' da ga možemo takvim proglasiti,btw brojeva sa tim svojstvom oko nule ima neprebrojivo mnogo,brojevi u neposrednoj okolini slijeva od nule također potpuno određuju nulu pa se njima ''čak i uklanja minus'' ).
[/quote]
Ne mozes broj razlicit od nule proglasiti nulom, je za razliku od nule pozitivni broj e ima svojstvo da je i e/2 pozitivan, sto je gore bilo jako korisno :wink:
Koje je to svojstvo brojeva oko nule i na koji nacin se to uklanja minus? :grebgreb:
[quote]
Dakle u definiciji Reiman integrabilnosti imamo jednakost I*=I ali ako ćemo biti ''Božje precizni'' to nije točno,jeli tako(sada sam to laički opisao),mislim ako ćemo biti ''B-O-Ž-J-E PRECIZNI''!
[/quote]
Ako cemo biti precizni i vise nego bozje ta jednakost mora vrijediti da bi neka funkcija bola R-integrabilna, a ta jenakost moze vrijediti jer supremum i infimum nekog skupa ne moraju biti elementi tog skupa, dakle ne moraju postojati (u dobrom djelu primjera i ne postoje) takve subdivizije d i d' da vrijedi S(d)=I* i S(d')=I
[quote]
I naravno,sada je jasno zašto _'za svaki'_ epsilon to zahtjevamo jer,zapravo nas boli briga za sve ostale epsilone kada mi imamo potvrdu kriterija za eps koji aproksimira nulu,onda je logično da će vrijediti i za svaki veći strogo pozitivan broj ako već vrijedi za broj blizak nuli.
[/quote]
Mogli smo mi zahtijevati da postoji delta>0 t.d za svaki pozitivan epsilon manji od delta vrijedi trazeno svojstvo, ali to je bespotrebna komplikacija, jer je ocito da tada to svojstvpo vrijedi za svaki epsilon>0. Takodjer, nema puno koristi od toga sto mi znamo da nesto vrijedi za jedan broj koji je [i]blizak[/i] nuli, jer ih ima neprebrojivo koji su blizi nuli. Zbog toga formulacija za svaki.
[quote]
I što znači 'invarijantan broj' ?
[/quote]
Kolega je vjerovatno zelio reci nevarijabilan, konstantan ili nesto u tom smislu.
:OT:[quote]_nema lažiranja_(nije to Dinamo-Rijeka)[/quote]
Mislis Rijeka - Osijek?
Prvo da rijesimo ono sa S(d)-s(d)⇐eps
Evo ovako: dokazali smo da za svaki pozitivni broj eps mozemo pronaci subdiviziju d t.d. S(d)-s(d)⇐eps.
OK, sada uzmimo proizvopljan e>0. Tada je i e/2 > 0. Po prethodno dokazanom postoji subdivizija d' t.d. S(d')-s(d')⇐e/2<e
Eto sada imamo strogu nejednakost.
| Citat: |
Za svaki eps>0 … pa si ja zemem epsilon zdesna od nule dovoljno malen da potpuno određuje nulu,dakle da ga slobodno možemo proglasiti nulom(imavši u vidu,da on nikada nije apsolutna nula ali joj je dovoljno ''blizak'' da ga možemo takvim proglasiti,btw brojeva sa tim svojstvom oko nule ima neprebrojivo mnogo,brojevi u neposrednoj okolini slijeva od nule također potpuno određuju nulu pa se njima ''čak i uklanja minus'' ).
|
Ne mozes broj razlicit od nule proglasiti nulom, je za razliku od nule pozitivni broj e ima svojstvo da je i e/2 pozitivan, sto je gore bilo jako korisno
Koje je to svojstvo brojeva oko nule i na koji nacin se to uklanja minus? 
| Citat: |
Dakle u definiciji Reiman integrabilnosti imamo jednakost I*=I ali ako ćemo biti ''Božje precizni'' to nije točno,jeli tako(sada sam to laički opisao),mislim ako ćemo biti ''B-O-Ž-J-E PRECIZNI''!
|
Ako cemo biti precizni i vise nego bozje ta jednakost mora vrijediti da bi neka funkcija bola R-integrabilna, a ta jenakost moze vrijediti jer supremum i infimum nekog skupa ne moraju biti elementi tog skupa, dakle ne moraju postojati (u dobrom djelu primjera i ne postoje) takve subdivizije d i d' da vrijedi S(d)=I* i S(d')=I
| Citat: |
I naravno,sada je jasno zašto _'za svaki'_ epsilon to zahtjevamo jer,zapravo nas boli briga za sve ostale epsilone kada mi imamo potvrdu kriterija za eps koji aproksimira nulu,onda je logično da će vrijediti i za svaki veći strogo pozitivan broj ako već vrijedi za broj blizak nuli.
|
Mogli smo mi zahtijevati da postoji delta>0 t.d za svaki pozitivan epsilon manji od delta vrijedi trazeno svojstvo, ali to je bespotrebna komplikacija, jer je ocito da tada to svojstvpo vrijedi za svaki epsilon>0. Takodjer, nema puno koristi od toga sto mi znamo da nesto vrijedi za jedan broj koji je blizak nuli, jer ih ima neprebrojivo koji su blizi nuli. Zbog toga formulacija za svaki.
| Citat: |
I što znači 'invarijantan broj' ?
|
Kolega je vjerovatno zelio reci nevarijabilan, konstantan ili nesto u tom smislu.
 | Citat: | | _nema lažiranja_(nije to Dinamo-Rijeka) |
Mislis Rijeka - Osijek?
_________________
Extraordinary claims require extraordinary evidence. – Carl Sagan
|
|
| [Vrh] |
|
ZELENIZUBNAPLANETIDO
SADE
Forumaš(ica)
Pridružen/a: 04. 03. 2004. (19:56:15)
Postovi: (54F)16
Lokacija: hm?
|
| Postano: 16:02 sri, 18. 8. 2004 Naslov: |
|
|
|
[quote="Anonymous"]ma znaš kak si ja razmišljam?-uzeli smo proizvoljno strogo pozitivan broj eps i za njega kroz dokaz dobili nejednakost S(d)-s(d)<=eps,dakle,ta razlika suma može biti jednaka broju eps,a ja to ne smijem imati zbog kriterija koji zahtjeva strogu nejednakost.
Ti kažeš,množi taj broj eps sa 2 i imaš strogu nejednakost(slažem se),ali,nije li to ''lažiranje'' ?
Uzeo sam _eps proizvoljno_ i dobio score koji nisam htio,_nema lažiranja_(nije to Dinamo-Rijeka),za proizvoljan eps ja bih morao moći dobiti _strogu nejednakost_,a ja ju nisam dobio.[/quote]
Sve je stvar oznake ;)
Ovo, dakle, imamo:
[latex](\forall \varepsilon>0) (\exists \delta \in \Delta)~ t.d. ~S(\delta)-s(\delta)+I^*-I_*=S(\delta)-s(\delta) \leq \varepsilon <2\varepsilon[/latex]
Sada nazovimo: [latex]\varepsilon`:=2\varepsilon[/latex]
i ponovno zapisemo isti izraz:
[latex](\forall \varepsilon`>0) (\exists \delta \in \Delta)~ t.d. ~S(\delta)-s(\delta)+I^*-I_*=S(\delta)-s(\delta) \leq \frac{\varepsilon`}{2} <\varepsilon`[/latex]
[quote="Anonymous"]A opet(pazi sad ovo;)),svjestan sam činjenice da se svaki strogo pozitivan broj 'pepsi' može napisati u obliku : pepsi :=2*eps za eps>0 .[/quote]
[quote="Anonymous"]Daj mi sad pomogni u razmišljanju,gdje griješim ?
:o[/quote]
Oba tvoja problema ;) su stvar nacina na koji ces nesto zapisati. Ako svaki A>0 ima neko svojstvo, onda to svojstvo ima i A/2 i 2A. U nasem slucaju, to je iskljucivo stvar nacina na koji cemo nesto nazvati. Pristup nasih profesora na predavanjima jest da, znajuci kamo ce ih dokaz voditi, na pocetku namijeste vrijednosti.
Elegantnije i minimalisticnije jest to, ali je barem meni, jednostavnije (buduci da mahom ne znam kamo dokaz vodi ;)) oznaciti na pocetku taj epsilon nekom drugom oznakom i onda kasnije namijestati. Oba pristupa su matematicki korektna, samo je pitanje izbora hoces li olaksati posao citaocu ili onome koji pise, a buduci da si ti taj koji pise.... ;)
[quote="Anonymous"]Hajde da još rezimiram što tvrdi kriterij integrabilnosti:
Za svaki eps>0 … pa si ja zemem epsilon zdesna od nule dovoljno malen da potpuno određuje nulu,dakle da ga slobodno možemo proglasiti nulom(imavši u vidu,da on nikada nije apsolutna nula ali joj je dovoljno ''blizak'' da ga možemo takvim proglasiti,btw brojeva sa tim svojstvom oko nule ima neprebrojivo mnogo,brojevi u neposrednoj okolini slijeva od nule također potpuno određuju nulu pa se njima ''čak i uklanja minus'' ).[/quote]
:shock: malo si me izgubio, ali NITI JEDAN BROJ OSIM NULE NE MOZEMO SLOBODNO PROGLASITI NULOM, bar ne u kontekstu ovog kolegija :shock:
i 2., brojeva u okolici nule koje mozemo "slobodno proglasiti nulom" ima koliko i realnih brojeva u totalu, ergo: svaki realni broj je 0 :g:
:-s [i]"uklanja minus"[/i] :-s
Kriterij (R)integrabilnosti kaze (slobodno) : fja je (R)integrabilna ako i samo ako za svaku po volji malu udaljenost mogu naci gornju i donju darbouxovu sumu koje ce biti "bliskije" od toga. ok?
[quote="Anonymous"]Kriterij je S(d)-s(d)<eps ,eps je mizerno veći od nule,dakle postoje takve Darboux-ove sume(donja i gornja) da vrijedi da je njihova razlika mizerna,naravno,te sume su I* i I.[/quote]
NENEnenenene e :) Te sume NISU I* i I :!: :) Za po volji "mizerni" :) realni broj veci od 0, postoje subdivizije intervala tako da su darbouxove sume za manje od te mizerne velicine udaljene od gornjeg, tj. donjeg (R)integrala :)
[quote="Anonymous"]Što te ja želim pitati ?
Dakle u definiciji Reiman integrabilnosti imamo jednakost I*=I ali ako ćemo biti ''Božje precizni'' to nije točno,jeli tako(sada sam to laički opisao),mislim ako ćemo biti ''B-O-Ž-J-E PRECIZNI''![/quote]
Ne, to je ipak BOZJEPRECIZNO :D Darbouxove sume nisu bozjeprecizno iste kao i njihovi (R)integrali ali ako su fje (R)integrabilne, tada je I*=I po definiciji :) (kada u svom udjbeniku vidis "=", onda to uistinu znaci "=" ;))
[quote="Anonymous"]I naravno,sada je jasno zašto _'za svaki'_ epsilon to zahtjevamo jer,zapravo nas boli briga za sve ostale epsilone kada mi imamo potvrdu kriterija za eps koji aproksimira nulu,onda je logično da će vrijediti i za svaki veći strogo pozitivan broj ako već vrijedi za broj blizak nuli.[/quote]
Odgovorit cu ti na ovo pitanje kada mi odgovoris koji je to najmanji epsilon za koji te boli briga a koji je najveci koji aproksimira 0 :g:
Poanta jest u tome da to nije bitno, formulacija ostvaruje svoju punu snagu za [url=http://www.procrastinators.org/googolplex.html]male velicine[/url], ali to uistinu nije bitno, jer propozicija uistinu i misli ono sto kaze :) every epsilon matters ;)
[quote="Anonymous"]Reci da imam pravo.:o)[/quote]
:pray: :)
[quote="Anonymous"]I što znači 'invarijantan broj' ?[/quote]
Neka zasad ostane samo pjesnicka slika :g:
Jeli ti jasno zasto je I*=I u zadnjoj liniji dokaza?
[quote]PS pise se "Darboux" [/quote]
[quote]Ma mogao sam si misliti da će uspješan matematičar u prezimenu imati nepoznanicu x,cccc.
:o)[/quote]
Zapravo, mislim da su u njegovo vrijeme koristili samoglasnike kao nepoznanice, tako da ga mozes zvati i Darbioue ako zbilja zelis :g:
[quote]ma prvo sam izgubio šifru,pa sam promijenio mail,pa sam rekao moderatoru da mi pošalje na novi mail pa je on rekao da mi ne vjeruje da sam ja ta osoba koja je imala izgubljenu šifru(što je logično jer nema dokaza;)) i tak me prošla volja za registriranjem…evo idem se regat na carnet,papirologiju sam sredio. 8)[/quote]
Ako izvadis besplatni mail na iskonu, umijesto da trcis na SRCE ili di vec, gotov si za 10 min?
| Anonymous (napisa): | ma znaš kak si ja razmišljam?-uzeli smo proizvoljno strogo pozitivan broj eps i za njega kroz dokaz dobili nejednakost S(d)-s(d)⇐eps,dakle,ta razlika suma može biti jednaka broju eps,a ja to ne smijem imati zbog kriterija koji zahtjeva strogu nejednakost.
Ti kažeš,množi taj broj eps sa 2 i imaš strogu nejednakost(slažem se),ali,nije li to ''lažiranje'' ?
Uzeo sam _eps proizvoljno_ i dobio score koji nisam htio,_nema lažiranja_(nije to Dinamo-Rijeka),za proizvoljan eps ja bih morao moći dobiti _strogu nejednakost_,a ja ju nisam dobio. |
Sve je stvar oznake
Ovo, dakle, imamo:
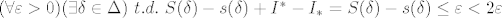
Sada nazovimo: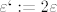 
i ponovno zapisemo isti izraz:
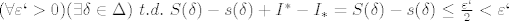
| Anonymous (napisa): | | A opet(pazi sad ovo;)),svjestan sam činjenice da se svaki strogo pozitivan broj 'pepsi' može napisati u obliku : pepsi :=2*eps za eps>0 . |
| Anonymous (napisa): | Daj mi sad pomogni u razmišljanju,gdje griješim ?
|
Oba tvoja problema su stvar nacina na koji ces nesto zapisati. Ako svaki A>0 ima neko svojstvo, onda to svojstvo ima i A/2 i 2A. U nasem slucaju, to je iskljucivo stvar nacina na koji cemo nesto nazvati. Pristup nasih profesora na predavanjima jest da, znajuci kamo ce ih dokaz voditi, na pocetku namijeste vrijednosti.
Elegantnije i minimalisticnije jest to, ali je barem meni, jednostavnije (buduci da mahom ne znam kamo dokaz vodi ) oznaciti na pocetku taj epsilon nekom drugom oznakom i onda kasnije namijestati. Oba pristupa su matematicki korektna, samo je pitanje izbora hoces li olaksati posao citaocu ili onome koji pise, a buduci da si ti taj koji pise....
| Anonymous (napisa): | Hajde da još rezimiram što tvrdi kriterij integrabilnosti:
Za svaki eps>0 … pa si ja zemem epsilon zdesna od nule dovoljno malen da potpuno određuje nulu,dakle da ga slobodno možemo proglasiti nulom(imavši u vidu,da on nikada nije apsolutna nula ali joj je dovoljno ''blizak'' da ga možemo takvim proglasiti,btw brojeva sa tim svojstvom oko nule ima neprebrojivo mnogo,brojevi u neposrednoj okolini slijeva od nule također potpuno određuju nulu pa se njima ''čak i uklanja minus'' ). |
 malo si me izgubio, ali NITI JEDAN BROJ OSIM NULE NE MOZEMO SLOBODNO PROGLASITI NULOM, bar ne u kontekstu ovog kolegija
i 2., brojeva u okolici nule koje mozemo "slobodno proglasiti nulom" ima koliko i realnih brojeva u totalu, ergo: svaki realni broj je 0 
 "uklanja minus"
Kriterij (R)integrabilnosti kaze (slobodno) : fja je (R)integrabilna ako i samo ako za svaku po volji malu udaljenost mogu naci gornju i donju darbouxovu sumu koje ce biti "bliskije" od toga. ok?
| Anonymous (napisa): | | Kriterij je S(d)-s(d)<eps ,eps je mizerno veći od nule,dakle postoje takve Darboux-ove sume(donja i gornja) da vrijedi da je njihova razlika mizerna,naravno,te sume su I* i I. |
NENEnenenene e Te sume NISU I* i I Za po volji "mizerni" realni broj veci od 0, postoje subdivizije intervala tako da su darbouxove sume za manje od te mizerne velicine udaljene od gornjeg, tj. donjeg (R)integrala
| Anonymous (napisa): | Što te ja želim pitati ?
Dakle u definiciji Reiman integrabilnosti imamo jednakost I*=I ali ako ćemo biti ''Božje precizni'' to nije točno,jeli tako(sada sam to laički opisao),mislim ako ćemo biti ''B-O-Ž-J-E PRECIZNI''! |
Ne, to je ipak BOZJEPRECIZNO  Darbouxove sume nisu bozjeprecizno iste kao i njihovi (R)integrali ali ako su fje (R)integrabilne, tada je I*=I po definiciji (kada u svom udjbeniku vidis "=", onda to uistinu znaci "=" )
| Anonymous (napisa): | | I naravno,sada je jasno zašto _'za svaki'_ epsilon to zahtjevamo jer,zapravo nas boli briga za sve ostale epsilone kada mi imamo potvrdu kriterija za eps koji aproksimira nulu,onda je logično da će vrijediti i za svaki veći strogo pozitivan broj ako već vrijedi za broj blizak nuli. |
Odgovorit cu ti na ovo pitanje kada mi odgovoris koji je to najmanji epsilon za koji te boli briga a koji je najveci koji aproksimira 0
Poanta jest u tome da to nije bitno, formulacija ostvaruje svoju punu snagu za male velicine, ali to uistinu nije bitno, jer propozicija uistinu i misli ono sto kaze every epsilon matters
| Anonymous (napisa): | | Reci da imam pravo. |
| Anonymous (napisa): | | I što znači 'invarijantan broj' ? |
Neka zasad ostane samo pjesnicka slika
Jeli ti jasno zasto je I*=I u zadnjoj liniji dokaza?
| Citat: | | PS pise se "Darboux" |
| Citat: | Ma mogao sam si misliti da će uspješan matematičar u prezimenu imati nepoznanicu x,cccc.
|
Zapravo, mislim da su u njegovo vrijeme koristili samoglasnike kao nepoznanice, tako da ga mozes zvati i Darbioue ako zbilja zelis
| Citat: | | ma prvo sam izgubio šifru,pa sam promijenio mail,pa sam rekao moderatoru da mi pošalje na novi mail pa je on rekao da mi ne vjeruje da sam ja ta osoba koja je imala izgubljenu šifru(što je logično jer nema dokaza;)) i tak me prošla volja za registriranjem…evo idem se regat na carnet,papirologiju sam sredio. |
Ako izvadis besplatni mail na iskonu, umijesto da trcis na SRCE ili di vec, gotov si za 10 min?
_________________
Pupoljak nije negiran. Rekao sam to i ponovit cu to jos jedanput. Pupoljak NIJE negirAn.
MADD
(Mothers Against Dirty Dialectics)
Based on a true story. NOT.
Ko ih sljivi, mi sviramo punk |
|
| [Vrh] |
|
Gost
|
| Postano: 17:56 sri, 18. 8. 2004 Naslov: |
|
|
|
[quote]Prvo da rijesimo ono sa S(d)-s(d)<=eps
Evo ovako: dokazali smo da za svaki pozitivni broj eps mozemo pronaci subdiviziju d t.d. S(d)-s(d)<=eps.
OK, sada uzmimo proizvopljan e>0. Tada je i e/2 > 0. Po prethodno dokazanom postoji subdivizija d' t.d. S(d')-s(d')<=e/2<e
Eto sada imamo strogu nejednakost.
[/quote]
Ok.
[quote]Koje je to svojstvo brojeva oko nule i na koji nacin se to uklanja minus? [/quote]
:silence: :grunt:
[quote]Mogli smo mi zahtijevati da postoji delta>0 t.d za svaki pozitivan epsilon manji od delta vrijedi trazeno svojstvo, ali to je bespotrebna komplikacija[/quote]
Evo vidiš,meni se tvoja formulacija više sviđa,nekako mi je minimalnija,hm…
[quote]Mislis Rijeka - Osijek?[/quote]
E da,da,koja nepravda.
[color=green]Za zelenog:[/color]
[quote]Oba tvoja problema su stvar nacina na koji ces nesto zapisati. Ako svaki A>0 ima neko svojstvo, onda to svojstvo ima i A/2 i 2A. U nasem slucaju, to je iskljucivo stvar nacina na koji cemo nesto nazvati. Pristup nasih profesora na predavanjima jest da, znajuci kamo ce ih dokaz voditi, na pocetku namijeste vrijednosti.
Elegantnije i minimalisticnije jest to, ali je barem meni, jednostavnije (buduci da mahom ne znam kamo dokaz vodi ) oznaciti na pocetku taj epsilon nekom drugom oznakom i onda kasnije namijestati. Oba pristupa su matematicki korektna, samo je pitanje izbora hoces li olaksati posao citaocu ili onome koji pise, a buduci da si ti taj koji pise....
[/quote]
Ajde da sam i to raskrstio. :relax:
[quote]i 2., brojeva u okolici nule koje mozemo "slobodno proglasiti nulom" ima koliko i realnih brojeva u totalu, ergo: svaki realni broj je 0 [/quote]
:ccc: ne mi to raditi,ne me zbunjivati :ccc:
:grebgreb:
[quote] "uklanja minus" [/quote]
:drinking:
[quote]Ne, to je ipak BOZJEPRECIZNO Darbouxove sume nisu bozjeprecizno iste kao i njihovi (R)integrali ali ako su fje (R)integrabilne, tada je I*=I po definiciji (kada u svom udjbeniku vidis "=", onda to uistinu znaci "=" )[/quote]
čitaj kako piše,čitaj kako piše,čitaj kako piše…ispisujem tu rečenicu u cijelu bilježnicu za kaznu.
[quote]Odgovorit cu ti na ovo pitanje kada mi odgovoris koji je to najmanji epsilon za koji te boli briga a koji je najveci koji aproksimira 0 [/quote]
Evo pogledat ću u uđbenik iz matke za osnovnu školu,znam da me je to već tamo zbunjivalo. :roll:
[quote]Zapravo, mislim da su u njegovo vrijeme koristili samoglasnike kao nepoznanice, tako da ga mozes zvati i Darbioue ako zbilja zelis [/quote]
=D> lijepo sročeno.
[quote]Ako izvadis besplatni mail na iskonu, umijesto da trcis na SRCE ili di vec, gotov si za 10 min?[/quote]
It is done.;)
| Citat: | Prvo da rijesimo ono sa S(d)-s(d)⇐eps
Evo ovako: dokazali smo da za svaki pozitivni broj eps mozemo pronaci subdiviziju d t.d. S(d)-s(d)⇐eps.
OK, sada uzmimo proizvopljan e>0. Tada je i e/2 > 0. Po prethodno dokazanom postoji subdivizija d' t.d. S(d')-s(d')⇐e/2<e
Eto sada imamo strogu nejednakost.
|
Ok.
| Citat: | | Koje je to svojstvo brojeva oko nule i na koji nacin se to uklanja minus? |
 
| Citat: | | Mogli smo mi zahtijevati da postoji delta>0 t.d za svaki pozitivan epsilon manji od delta vrijedi trazeno svojstvo, ali to je bespotrebna komplikacija |
Evo vidiš,meni se tvoja formulacija više sviđa,nekako mi je minimalnija,hm…
| Citat: | | Mislis Rijeka - Osijek? |
E da,da,koja nepravda.
Za zelenog:
| Citat: | Oba tvoja problema su stvar nacina na koji ces nesto zapisati. Ako svaki A>0 ima neko svojstvo, onda to svojstvo ima i A/2 i 2A. U nasem slucaju, to je iskljucivo stvar nacina na koji cemo nesto nazvati. Pristup nasih profesora na predavanjima jest da, znajuci kamo ce ih dokaz voditi, na pocetku namijeste vrijednosti.
Elegantnije i minimalisticnije jest to, ali je barem meni, jednostavnije (buduci da mahom ne znam kamo dokaz vodi ) oznaciti na pocetku taj epsilon nekom drugom oznakom i onda kasnije namijestati. Oba pristupa su matematicki korektna, samo je pitanje izbora hoces li olaksati posao citaocu ili onome koji pise, a buduci da si ti taj koji pise....
|
Ajde da sam i to raskrstio. 
| Citat: | | i 2., brojeva u okolici nule koje mozemo "slobodno proglasiti nulom" ima koliko i realnih brojeva u totalu, ergo: svaki realni broj je 0 |
 ne mi to raditi,ne me zbunjivati
| Citat: | | Ne, to je ipak BOZJEPRECIZNO Darbouxove sume nisu bozjeprecizno iste kao i njihovi (R)integrali ali ako su fje (R)integrabilne, tada je I*=I po definiciji (kada u svom udjbeniku vidis "=", onda to uistinu znaci "=" ) |
čitaj kako piše,čitaj kako piše,čitaj kako piše…ispisujem tu rečenicu u cijelu bilježnicu za kaznu.
| Citat: | | Odgovorit cu ti na ovo pitanje kada mi odgovoris koji je to najmanji epsilon za koji te boli briga a koji je najveci koji aproksimira 0 |
Evo pogledat ću u uđbenik iz matke za osnovnu školu,znam da me je to već tamo zbunjivalo. 
| Citat: | | Zapravo, mislim da su u njegovo vrijeme koristili samoglasnike kao nepoznanice, tako da ga mozes zvati i Darbioue ako zbilja zelis |
 lijepo sročeno.
| Citat: | | Ako izvadis besplatni mail na iskonu, umijesto da trcis na SRCE ili di vec, gotov si za 10 min? |
It is done.
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
Vincent Van Ear
Forumaš(ica)
Pridružen/a: 19. 08. 2004. (11:29:05)
Postovi: (175)16
|
| Postano: 13:06 čet, 19. 8. 2004 Naslov: |
|
|
|
I još nešto.
Kriterij integrabilnosti pretpostavlja realnu funkciju na segmentu i _omeđenu_.
Naravno,ja neću pogriješiti ako u pretpostavku uzmem realnu funkciju na segmentu i neprekidnu,jer kolege Bolzano i Weierstrass(spokoj im u duši;)) kažu da će takva funkcija sigurno biti omeđena,jedino što sam si tom pretpostavkom restrinigirao velik broj omeđenih funkcija za koje onda kriterij integrabilnosti ne govori ništa,pritom mislim na omeđene koje nisu neprekidne.
I još nešto.
Kriterij integrabilnosti pretpostavlja realnu funkciju na segmentu i _omeđenu_.
Naravno,ja neću pogriješiti ako u pretpostavku uzmem realnu funkciju na segmentu i neprekidnu,jer kolege Bolzano i Weierstrass(spokoj im u duši) kažu da će takva funkcija sigurno biti omeđena,jedino što sam si tom pretpostavkom restrinigirao velik broj omeđenih funkcija za koje onda kriterij integrabilnosti ne govori ništa,pritom mislim na omeđene koje nisu neprekidne.
_________________
Samo sam jedan čovjek,
samo jedan pakao.
|
|
| [Vrh] |
|
mdoko
Forumaš(ica)
Pridružen/a: 30. 11. 2002. (22:17:12)
Postovi: (71A)16
Spol:
Lokacija: Heriot-Watt University, Edinburgh
|
| Postano: 23:11 čet, 19. 8. 2004 Naslov: |
|
|
|
[quote][quote="mdoko"]
Mogli smo mi zahtijevati da postoji delta>0 t.d za svaki pozitivan epsilon manji od delta vrijedi trazeno svojstvo, ali to je bespotrebna komplikacija
[/quote]
Evo vidiš,meni se tvoja formulacija više sviđa,nekako mi je minimalnija,hm…
[/quote]
Nije minimalnija, ekvivalentna je :!:
U mom prethodnom postu je dokazano da gornja formulacija povlaci onu iz uvjeta teorema, a trebalo bi biti ocito da formulacija 'za svaki...' povlaci gore navedenu. :wink:
| Citat: | | mdoko (napisa): |
Mogli smo mi zahtijevati da postoji delta>0 t.d za svaki pozitivan epsilon manji od delta vrijedi trazeno svojstvo, ali to je bespotrebna komplikacija
|
Evo vidiš,meni se tvoja formulacija više sviđa,nekako mi je minimalnija,hm…
|
Nije minimalnija, ekvivalentna je
U mom prethodnom postu je dokazano da gornja formulacija povlaci onu iz uvjeta teorema, a trebalo bi biti ocito da formulacija 'za svaki...' povlaci gore navedenu.
_________________
Extraordinary claims require extraordinary evidence. – Carl Sagan
|
|
| [Vrh] |
|
Vincent Van Ear
Forumaš(ica)
Pridružen/a: 19. 08. 2004. (11:29:05)
Postovi: (175)16
|
| Postano: 14:21 pet, 20. 8. 2004 Naslov: |
|
|
|
[quote]Nije minimalnija, ekvivalentna je
U mom prethodnom postu je dokazano da gornja formulacija povlaci onu iz uvjeta teorema, a trebalo bi biti ocito da formulacija 'za svaki...' povlaci gore navedenu. [/quote]
Imaš praf :wink:
I onda finalno,slobodnom interpretacijom usudio bih se opisati što tvrdi kriterij :
Koliko god malen strogo pozitivan broj uzeo ja ću naći subdiviziju sa svojstvom da je razlika gornje i donje Darbuox-ove sume manja od toga broja,dakle granična vrijednost(limes) tih razlika suma ide u nulu što je za očekivati s obzirom na pretpostavku da je f Reiman integrabilna.
Over&Out
| Citat: | Nije minimalnija, ekvivalentna je
U mom prethodnom postu je dokazano da gornja formulacija povlaci onu iz uvjeta teorema, a trebalo bi biti ocito da formulacija 'za svaki...' povlaci gore navedenu. |
Imaš praf
I onda finalno,slobodnom interpretacijom usudio bih se opisati što tvrdi kriterij :
Koliko god malen strogo pozitivan broj uzeo ja ću naći subdiviziju sa svojstvom da je razlika gornje i donje Darbuox-ove sume manja od toga broja,dakle granična vrijednost(limes) tih razlika suma ide u nulu što je za očekivati s obzirom na pretpostavku da je f Reiman integrabilna.
Over&Out
_________________
Samo sam jedan čovjek,
samo jedan pakao.
|
|
| [Vrh] |
|
ZELENIZUBNAPLANETIDO
SADE
Forumaš(ica)
Pridružen/a: 04. 03. 2004. (19:56:15)
Postovi: (54F)16
Lokacija: hm?
|
| Postano: 15:04 pet, 20. 8. 2004 Naslov: |
|
|
|
[quote="Vincent Van Ear"]Koliko god malen strogo pozitivan broj uzeo ja ću naći subdiviziju sa svojstvom da je razlika gornje i donje Darbuox-ove sume manja od toga broja,dakle [color=red]granična vrijednost(limes)[/color] tih razlika suma ide u nulu što je za očekivati s obzirom na pretpostavku da je f Reiman integrabilna.[/quote]
manja zamjerka: "limes" smo definirali (za sada) samo za realne fje i nizove, ne za skupove subdivizija
inace: bingo :D
| Vincent Van Ear (napisa): | | Koliko god malen strogo pozitivan broj uzeo ja ću naći subdiviziju sa svojstvom da je razlika gornje i donje Darbuox-ove sume manja od toga broja,dakle granična vrijednost(limes) tih razlika suma ide u nulu što je za očekivati s obzirom na pretpostavku da je f Reiman integrabilna. |
manja zamjerka: "limes" smo definirali (za sada) samo za realne fje i nizove, ne za skupove subdivizija
inace: bingo
_________________
Pupoljak nije negiran. Rekao sam to i ponovit cu to jos jedanput. Pupoljak NIJE negirAn.
MADD
(Mothers Against Dirty Dialectics)
Based on a true story. NOT.
Ko ih sljivi, mi sviramo punk |
|
| [Vrh] |
|
Vincent Van Ear
Forumaš(ica)
Pridružen/a: 19. 08. 2004. (11:29:05)
Postovi: (175)16
|
|
| [Vrh] |
|
|
