| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
Buki
Forumaš(ica)

Pridružen/a: 17. 10. 2010. (20:15:17)
Postovi: (56)16
|
|
| [Vrh] |
|
Phoenix
Forumaš(ica)


Pridružen/a: 15. 05. 2010. (18:46:07)
Postovi: (164)16
Sarma: -
|
 Postano: 16:17 pet, 18. 1. 2013 Naslov: Postano: 16:17 pet, 18. 1. 2013 Naslov: |
    |
|
|
Ovo što je napisano u tvom postu je otprilike to. :P
Evo ti i "formalnije":
[tex](0,0,z) \in A, \forall z \in \mathbb{R}[/tex], pa [tex](\forall M>0) (\exists z \in \mathbb{R}) M<\left\| (0,0,z) \right\|[/tex]. Odnosno, ne postoji otvorena kugla dovoljno velika da obuhvati sve točke. :)
Slično i s drugim skupom, uz, recimo, [tex](x,0,2) \in B, \forall x \in \mathbb{R}[/tex].
Ovo što je napisano u tvom postu je otprilike to. 
Evo ti i "formalnije":
[tex](0,0,z) \in A, \forall z \in \mathbb{R}[/tex], pa [tex](\forall M>0) (\exists z \in \mathbb{R}) M<\left\| (0,0,z) \right\|[/tex]. Odnosno, ne postoji otvorena kugla dovoljno velika da obuhvati sve točke. 
Slično i s drugim skupom, uz, recimo, [tex](x,0,2) \in B, \forall x \in \mathbb{R}[/tex].
|
|
| [Vrh] |
|
Vishykc
Forumaš(ica)


Pridružen/a: 23. 10. 2010. (14:38:08)
Postovi: (6A)16
Spol: 
Lokacija: Zagreb
|
|
| [Vrh] |
|
Phoenix
Forumaš(ica)


Pridružen/a: 15. 05. 2010. (18:46:07)
Postovi: (164)16
Sarma: -
|
|
| [Vrh] |
|
Vishykc
Forumaš(ica)


Pridružen/a: 23. 10. 2010. (14:38:08)
Postovi: (6A)16
Spol: 
Lokacija: Zagreb
|
 Postano: 19:55 pet, 18. 1. 2013 Naslov: Postano: 19:55 pet, 18. 1. 2013 Naslov: |
    |
|
|
Pa ne mora biti otvoren, ograničen, kompaktan ili? Ne vrijede ovi teoremi za nepr. fje na kompaktima, a onda se sve može dogoditi, ne? U principu ne znam jel sam za išta od toga u pravu. U biti cijeli zadatak, molim, legendarni Phoenixe! (btw. hvala na rješenjima svih onih kolokvija. Love you man, no homo! :lol: )
Pa ne mora biti otvoren, ograničen, kompaktan ili? Ne vrijede ovi teoremi za nepr. fje na kompaktima, a onda se sve može dogoditi, ne? U principu ne znam jel sam za išta od toga u pravu. U biti cijeli zadatak, molim, legendarni Phoenixe! (btw. hvala na rješenjima svih onih kolokvija. Love you man, no homo!  ) )
_________________
U matematici se sve smije, osim pogriješiti!
|
|
| [Vrh] |
|
pedro
Forumaš(ica)

Pridružen/a: 21. 10. 2010. (14:08:21)
Postovi: (19B)16
|
 Postano: 22:07 pet, 18. 1. 2013 Naslov: Postano: 22:07 pet, 18. 1. 2013 Naslov: |
    |
|
|
[quote="Phoenix"]Ovo što je napisano u tvom postu je otprilike to. :P
Evo ti i "formalnije":
[tex](0,0,z) \in A, \forall z \in \mathbb{R}[/tex], pa [tex](\forall M>0) (\exists z \in \mathbb{R}) M<\left\| (0,0,z) \right\|[/tex]. Odnosno, ne postoji otvorena kugla dovoljno velika da obuhvati sve točke. :)
Slično i s drugim skupom, uz, recimo, [tex](x,0,2) \in B, \forall x \in \mathbb{R}[/tex].[/quote]
znači, ne treba ovako formalno? :D
ja bi ograničila u A: x i y i onda bi napisala da je z proizvoljan iz R te kako nije ograničen nije ni A
i imam pitanje za skup B, je li u ovom slučaju koordinata z ograničena? i kako da nju ograničimo, nekak sam skužila kako i zašto ide kad imamo varijablu ^2 al za ove bez nebih znala baš :S
[size=9][color=#999999]Added after 6 minutes:[/color][/size]
i kako rješiti pod c)
A je zatvoren i B je zatvoren
A presjek B je zatvoren kao konačan presjek zatvorenih skupova
kako pokazati ograničenost? po mogućnosti bez crtanja :D
[size=9][color=#999999]Added after 16 minutes:[/color][/size]
nvm, skužila sam :D
dobila sam da je ograničen presjek i to ovako:
-sqrt6 <= x <= sqrt6
-sqrt2 <= y <= sqrt2
0 <= z <= 2
molim nekog za provjeru
| Phoenix (napisa): | Ovo što je napisano u tvom postu je otprilike to. 
Evo ti i "formalnije":
[tex](0,0,z) \in A, \forall z \in \mathbb{R}[/tex], pa [tex](\forall M>0) (\exists z \in \mathbb{R}) M<\left\| (0,0,z) \right\|[/tex]. Odnosno, ne postoji otvorena kugla dovoljno velika da obuhvati sve točke. 
Slično i s drugim skupom, uz, recimo, [tex](x,0,2) \in B, \forall x \in \mathbb{R}[/tex]. |
znači, ne treba ovako formalno? 
ja bi ograničila u A: x i y i onda bi napisala da je z proizvoljan iz R te kako nije ograničen nije ni A
i imam pitanje za skup B, je li u ovom slučaju koordinata z ograničena? i kako da nju ograničimo, nekak sam skužila kako i zašto ide kad imamo varijablu ^2 al za ove bez nebih znala baš :S
Added after 6 minutes:
i kako rješiti pod c)
A je zatvoren i B je zatvoren
A presjek B je zatvoren kao konačan presjek zatvorenih skupova
kako pokazati ograničenost? po mogućnosti bez crtanja 
Added after 16 minutes:
nvm, skužila sam 
dobila sam da je ograničen presjek i to ovako:
-sqrt6 ⇐ x ⇐ sqrt6
-sqrt2 ⇐ y ⇐ sqrt2
0 ⇐ z ⇐ 2
molim nekog za provjeru
|
|
| [Vrh] |
|
pbakic
Forumaš(ica)

Pridružen/a: 05. 10. 2009. (17:48:30)
Postovi: (143)16
Spol: 
|
 Postano: 22:12 pet, 18. 1. 2013 Naslov: Postano: 22:12 pet, 18. 1. 2013 Naslov: |
    |
|
|
[quote="Vishykc"]Pa ne mora biti otvoren, ograničen, kompaktan ili? Ne vrijede ovi teoremi za nepr. fje na kompaktima, a onda se sve može dogoditi, ne? U principu ne znam jel sam za išta od toga u pravu. U biti cijeli zadatak, molim, legendarni Phoenixe! (btw. hvala na rješenjima svih onih kolokvija. Love you man, no homo! :lol: )[/quote]
Eo da malo rasteretim Phoenixa :)
a) nije: uzmimo f konstantu - slika je jedna tocka, a to nije otvoren skup
b) f(x,y)=1/x - slika nije ogranicena. posebno, nije ni kompaktna.
c) A je ocito putevima povezan (pp) pa pa je i njegova slika po neprekidnoj funkciji pp (to se pokaze na predavanjima). Posebno, f(A) je povezan (jer je svaki pp skup i obicno povezan)
d) Ako zelis bit drzak, stavis f(x,y)=1, f(x,y)=2, f(x,y)=3 :P
Ako ne, malo se potrudis, al nemoj si zadat nista pretesko :D
@pedro: ovo tvoje izgleda ok
| Vishykc (napisa): | Pa ne mora biti otvoren, ograničen, kompaktan ili? Ne vrijede ovi teoremi za nepr. fje na kompaktima, a onda se sve može dogoditi, ne? U principu ne znam jel sam za išta od toga u pravu. U biti cijeli zadatak, molim, legendarni Phoenixe! (btw. hvala na rješenjima svih onih kolokvija. Love you man, no homo!  ) ) |
Eo da malo rasteretim Phoenixa 
a) nije: uzmimo f konstantu - slika je jedna tocka, a to nije otvoren skup
b) f(x,y)=1/x - slika nije ogranicena. posebno, nije ni kompaktna.
c) A je ocito putevima povezan (pp) pa pa je i njegova slika po neprekidnoj funkciji pp (to se pokaze na predavanjima). Posebno, f(A) je povezan (jer je svaki pp skup i obicno povezan)
d) Ako zelis bit drzak, stavis f(x,y)=1, f(x,y)=2, f(x,y)=3 
Ako ne, malo se potrudis, al nemoj si zadat nista pretesko 
@pedro: ovo tvoje izgleda ok
|
|
| [Vrh] |
|
pedro
Forumaš(ica)

Pridružen/a: 21. 10. 2010. (14:08:21)
Postovi: (19B)16
|
|
| [Vrh] |
|
Phoenix
Forumaš(ica)


Pridružen/a: 15. 05. 2010. (18:46:07)
Postovi: (164)16
Sarma: -
|
|
| [Vrh] |
|
pedro
Forumaš(ica)

Pridružen/a: 21. 10. 2010. (14:08:21)
Postovi: (19B)16
|
 Postano: 10:56 sub, 19. 1. 2013 Naslov: Postano: 10:56 sub, 19. 1. 2013 Naslov: |
    |
|
|
3. b)
imamo f(x,y)=x*y uz uvjet x^2+y^2=16
kad to sve porješavam dobijem da su točke u kojima se postižu ekstremi
(+/-2,+/-2)
e sad tražimalo max površinu, odnosno max, a postiže se za x=-2 i y=-2 ,
x=2 i y=2
kako su x,y duljine stranica ja onda gledam rješenje samo za x=2 i y=2???
3.a) muči me stacinoarna točka (0,4/3) nikako ne mogu odrediti karakter :S
[size=9][color=#999999]Added after 32 minutes:[/color][/size]
5.a )
ne shvaćam baš što me traže
ja sam ovako
def sam f(x,y)=(x,y)
i f je neprekidna ako i samo ako su joj sve komponente neprekidne, x je projekcija i y je projekcija, a to su neprekidne fun, f je neprekidna
trebam li još dodatno šta dokazati, napisati?
3. b)
imamo f(x,y)=x*y uz uvjet x^2+y^2=16
kad to sve porješavam dobijem da su točke u kojima se postižu ekstremi
(+/-2,+/-2)
e sad tražimalo max površinu, odnosno max, a postiže se za x=-2 i y=-2 ,
x=2 i y=2
kako su x,y duljine stranica ja onda gledam rješenje samo za x=2 i y=2???
3.a) muči me stacinoarna točka (0,4/3) nikako ne mogu odrediti karakter :S
Added after 32 minutes:
5.a )
ne shvaćam baš što me traže
ja sam ovako
def sam f(x,y)=(x,y)
i f je neprekidna ako i samo ako su joj sve komponente neprekidne, x je projekcija i y je projekcija, a to su neprekidne fun, f je neprekidna
trebam li još dodatno šta dokazati, napisati?
|
|
| [Vrh] |
|
Phoenix
Forumaš(ica)


Pridružen/a: 15. 05. 2010. (18:46:07)
Postovi: (164)16
Sarma: -
|
 Postano: 12:46 sub, 19. 1. 2013 Naslov: Postano: 12:46 sub, 19. 1. 2013 Naslov: |
    |
|
|
3. b) Da, točno tako. :)
(Doduše, uz [tex]x=y=2 \sqrt{2}[/tex], ali dobro, brojke nisu toliko bitne ovdje. :))
3. a) [tex]\Delta_1 = 2, \Delta_2 = -8[/tex]. Upravo ovaj niz je sedlastog tipa pa je Hesseova matrica u toj točki indefinitna (Profinjeni Sylvesterov kriterij s vježbi). Stoga je [tex]\left( 0, \frac{4}{3} \right)[/tex] sedlastog tipa (teorem [tex]16.7[/tex] s predavanja).
5. a) Da, to je to. :) Možda bi htjeli da pokažeš i da su funkcije komponente [tex](x,y) \mapsto x[/tex] te [tex](x,y) \mapsto y[/tex] neprekidne, ali to su funkcije projekcije i to je pojašnjeno u primjeru [tex]6.11[/tex] s predavanja. :)
3. b) Da, točno tako. 
(Doduše, uz [tex]x=y=2 \sqrt{2}[/tex], ali dobro, brojke nisu toliko bitne ovdje.  ) )
3. a) [tex]\Delta_1 = 2, \Delta_2 = -8[/tex]. Upravo ovaj niz je sedlastog tipa pa je Hesseova matrica u toj točki indefinitna (Profinjeni Sylvesterov kriterij s vježbi). Stoga je [tex]\left( 0, \frac{4}{3} \right)[/tex] sedlastog tipa (teorem [tex]16.7[/tex] s predavanja).
5. a) Da, to je to.  Možda bi htjeli da pokažeš i da su funkcije komponente [tex](x,y) \mapsto x[/tex] te [tex](x,y) \mapsto y[/tex] neprekidne, ali to su funkcije projekcije i to je pojašnjeno u primjeru [tex]6.11[/tex] s predavanja. Možda bi htjeli da pokažeš i da su funkcije komponente [tex](x,y) \mapsto x[/tex] te [tex](x,y) \mapsto y[/tex] neprekidne, ali to su funkcije projekcije i to je pojašnjeno u primjeru [tex]6.11[/tex] s predavanja. 
|
|
| [Vrh] |
|
pedro
Forumaš(ica)

Pridružen/a: 21. 10. 2010. (14:08:21)
Postovi: (19B)16
|
|
| [Vrh] |
|
an5
Forumaš(ica)
Pridružen/a: 13. 09. 2012. (20:48:55)
Postovi: (9)16
|
|
| [Vrh] |
|
Phoenix
Forumaš(ica)


Pridružen/a: 15. 05. 2010. (18:46:07)
Postovi: (164)16
Sarma: -
|
 Postano: 16:04 sub, 19. 1. 2013 Naslov: Postano: 16:04 sub, 19. 1. 2013 Naslov: |
    |
|
|
4. b) Za [tex]f(x,y):=(0,0)[/tex] vrijedi [tex]f(1,1)-f(0,0)=(0,0)=Df(x,y)((1,1)-(0,0)), \forall (x,y) \in \mathbb{R}^2[/tex].
S druge strane, za [tex]f(x,y):=\left\{ \begin{array}{rcl}
(1,1) & x,y>\frac{1}{2} \\ (0,0) & x \leq \frac{1}{2} \mathrm{ili} y \leq \frac{1}{2}
\end{array}\right.[/tex] vrijedi [tex]f(1,1)-f(0,0)=(1,1)[/tex], no [tex]Df(x,y)((1,1)-(0,0))=(0,0)[/tex] za svaku točku [tex](x,y) \in \mathbb{R}^2[/tex] za koju [tex]Df[/tex] postoji (jer je u okolini te točke [tex]f[/tex] konstanta).
5. b) [tex]f(x,0)=x^3[/tex] pa [tex]f |_{\mathbb{R} \times \left\{ 0 \right\}}[/tex] nema ni globalni minimum ni globalni maksimum, pa iste tvrdnje vrijede i za [tex]f[/tex].
4. b) Za [tex]f(x,y):=(0,0)[/tex] vrijedi [tex]f(1,1)-f(0,0)=(0,0)=Df(x,y)((1,1)-(0,0)), \forall (x,y) \in \mathbb{R}^2[/tex].
S druge strane, za [tex]f(x,y):=\left\{ \begin{array}{rcl}
(1,1) & x,y>\frac{1}{2} \\ (0,0) & x \leq \frac{1}{2} \mathrm{ili} y \leq \frac{1}{2}
\end{array}\right.[/tex] vrijedi [tex]f(1,1)-f(0,0)=(1,1)[/tex], no [tex]Df(x,y)((1,1)-(0,0))=(0,0)[/tex] za svaku točku [tex](x,y) \in \mathbb{R}^2[/tex] za koju [tex]Df[/tex] postoji (jer je u okolini te točke [tex]f[/tex] konstanta).
5. b) [tex]f(x,0)=x^3[/tex] pa [tex]f |_{\mathbb{R} \times \left\{ 0 \right\}}[/tex] nema ni globalni minimum ni globalni maksimum, pa iste tvrdnje vrijede i za [tex]f[/tex].
|
|
| [Vrh] |
|
angelika
Forumaš(ica)

Pridružen/a: 08. 02. 2011. (17:26:51)
Postovi: (5F)16
|
|
| [Vrh] |
|
moni_poni
Forumaš(ica)

Pridružen/a: 25. 01. 2010. (19:48:19)
Postovi: (49)16
|
|
| [Vrh] |
|
nuclear
Forumaš(ica)


Pridružen/a: 13. 11. 2011. (17:40:12)
Postovi: (74)16
Spol: 
|
 Postano: 20:53 sub, 19. 1. 2013 Naslov: Postano: 20:53 sub, 19. 1. 2013 Naslov: |
    |
|
|
http://web.math.pmf.unizg.hr/nastava/difraf/dif/2009-10/zavrsni.pdf
1. zadatak, pod a)
Je li ovo dovoljno dobro objašnjenje? Nekako, svaki put kad idem nešto dokazivati, izgubim pola bodova a ne znam gdje griješim.. :
definiramo funkciju [latex]f: R^3->R f(x,y,z)=x^2+3y^2-6[/latex]
Funkcija f je neprekidna funkcija kao zbroj, umnožak neprekidnih funkcija i projekcije:
[latex]p_1:R^3->R[/latex] [latex]p_1(x,y,z)=x[/latex]
[latex]p_2:R^3->R[/latex] [latex]p_2(x,y,z)=y[/latex]
[latex]g_1:R->R[/latex] [latex]g_1(x)=x^2[/latex]
[latex]f=g_1(p_1) + 3g_1(p_2) -6[/latex]
nadalje, jer je funkcija neprekidna, i vrijedi da je [latex]f<=0[/latex], odnosno slika funkcije f je (ne znam baš sve u lateksu) <-besk, 0] je zatvoren skup, pa je i njena praslika zatvoren skup, odnosno A=praslika(tntn..) je zatvoren skup.
[size=9][color=#999999]Added after 29 minutes:[/color][/size]
http://web.math.pmf.unizg.hr/nastava/difraf/dif/2009-10/zavrsni.pdf
čini mi se da krivo deriviram :D
2. zadatak:
računah derivaciju od f po [latex]x_j[/latex]:
[latex]1/(||x||^2) 2x_j cos( a_1x_1+...a_nx_n) - ln(||x||^2)sin(a_1x_1+...a_nx_n)a [/latex]
ovih tjedan dana prođe i zaboravih derivirati :shell:
http://web.math.pmf.unizg.hr/nastava/difraf/dif/2009-10/zavrsni.pdf
1. zadatak, pod a)
Je li ovo dovoljno dobro objašnjenje? Nekako, svaki put kad idem nešto dokazivati, izgubim pola bodova a ne znam gdje griješim.. :
definiramo funkciju 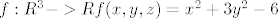
Funkcija f je neprekidna funkcija kao zbroj, umnožak neprekidnih funkcija i projekcije:
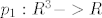 
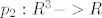 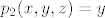
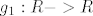 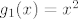
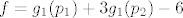
nadalje, jer je funkcija neprekidna, i vrijedi da je 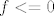 , odnosno slika funkcije f je (ne znam baš sve u lateksu) ←besk, 0] je zatvoren skup, pa je i njena praslika zatvoren skup, odnosno A=praslika(tntn..) je zatvoren skup. , odnosno slika funkcije f je (ne znam baš sve u lateksu) ←besk, 0] je zatvoren skup, pa je i njena praslika zatvoren skup, odnosno A=praslika(tntn..) je zatvoren skup.
Added after 29 minutes:
http://web.math.pmf.unizg.hr/nastava/difraf/dif/2009-10/zavrsni.pdf
čini mi se da krivo deriviram 
2. zadatak:
računah derivaciju od f po 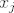 : :
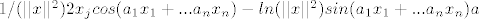
ovih tjedan dana prođe i zaboravih derivirati 
|
|
| [Vrh] |
|
Loo
Forumaš(ica)


Pridružen/a: 11. 06. 2012. (16:02:07)
Postovi: (D0)16
Spol: 
|
 Postano: 21:03 sub, 19. 1. 2013 Naslov: Postano: 21:03 sub, 19. 1. 2013 Naslov: |
    |
|
|
[quote="angelika"]http://web.math.pmf.unizg.hr/nastava/difraf/z2009.pdf
može mala pomoć sa 2.zadatkom? Kako da odredim područje diferencijabilnosti?
i kako u 1.zad provjeriti da li je skup povezan?[/quote]
1. skup je povezan ako se ne može rastaviti na uniju dva neprazna disjunktna skupa koji su otvoreni/zatvoreni u tom skupu.
s obzirom na to kako je skup zadan, možemo pokušati vidjeti koje će to točke biti u tom skupu.
vrijedit će
[tex](|x|+|y|-1)(x^2+y^2-\frac {1}{4})=0[/tex]
akko
[tex]|x|+|y|-1=0[/tex] ili [tex]x^2+y^2-\frac {1}{4}=0[/tex]
dakle ako definiramo funkcije
[tex]f_1(x,y)=|x|+|y|-1, f_2(x,y)=x^2+y^2-\frac {1}{4}[/tex] tada će vrijediti [tex]A=f_1^{-1}(\{0\})\cup f_2^{-1}(\{0\})[/tex]
funkcije su neprekidne, [tex]\{0\}[/tex] je zatvoren, pa su ove dvije praslike zatvoreni skupovi.
sada bi bilo super kada bi uspjeli dokazati da su te dvije praslike disjunktne jer tada [tex]A[/tex] nije povezan.
rješavamo sustav jer za točke u presjeku moraju vrijediti obje jednakosti:
[tex]|x|+|y|-1=0[/tex]
[tex]x^2+y^2-\frac {1}{4}=0[/tex]
te vidimo da ovaj sustav nema rješenja (izrazimo [tex]|y|[/tex] pomoću [tex]|x|[/tex] i ispadne nekakva negativna diskriminanta).
i to je to, skup se može rastaviti na uniju disjunktnih skupova koji su zatvoreni u A, pa nije povezan.
dobro, još je uvjet i da budu neprazni, pa bi bilo zgodno spomenuti da vrijedi npr. [tex](1,0)\in f_1^{-1}(\{0\}), (\frac {1}{2},0) \in f_2^{-1}(\{0\})[/tex]
[size=9][color=#999999]Added after 9 minutes:[/color][/size]
a što se tiče područja diferencijabilnosti, uvijek tražiš najveće moguće otvorene skupove na kojima je očito da je funkcija diferencijabilna.
u ovom slučaju to su:
[tex]\{(x,y) \in R^2: x+y>2\}, \{(x,y) \in R^2: 0<x+y<2\}, \{(x,y)\in R^2: x+y<0\}[/tex]
naravno treba argumentirati zašto su otvoreni i zašto je funkcija diferencijabilna (čisto šablonski)
i onda ispituješ što je sa rubovima tih skupova.
ako si prethodno uspjela dobiti da na nekom od tih rubova funkcija nije neprekidna, onda je to super jer u tim točkama onda ne trebaš ispitivati diferencijabilnost :wink:
| angelika (napisa): | http://web.math.pmf.unizg.hr/nastava/difraf/z2009.pdf
može mala pomoć sa 2.zadatkom? Kako da odredim područje diferencijabilnosti?
i kako u 1.zad provjeriti da li je skup povezan? |
1. skup je povezan ako se ne može rastaviti na uniju dva neprazna disjunktna skupa koji su otvoreni/zatvoreni u tom skupu.
s obzirom na to kako je skup zadan, možemo pokušati vidjeti koje će to točke biti u tom skupu.
vrijedit će
[tex](|x|+|y|-1)(x^2+y^2-\frac {1}{4})=0[/tex]
akko
[tex]|x|+|y|-1=0[/tex] ili [tex]x^2+y^2-\frac {1}{4}=0[/tex]
dakle ako definiramo funkcije
[tex]f_1(x,y)=|x|+|y|-1, f_2(x,y)=x^2+y^2-\frac {1}{4}[/tex] tada će vrijediti [tex]A=f_1^{-1}(\{0\})\cup f_2^{-1}(\{0\})[/tex]
funkcije su neprekidne, [tex]\{0\}[/tex] je zatvoren, pa su ove dvije praslike zatvoreni skupovi.
sada bi bilo super kada bi uspjeli dokazati da su te dvije praslike disjunktne jer tada [tex]A[/tex] nije povezan.
rješavamo sustav jer za točke u presjeku moraju vrijediti obje jednakosti:
[tex]|x|+|y|-1=0[/tex]
[tex]x^2+y^2-\frac {1}{4}=0[/tex]
te vidimo da ovaj sustav nema rješenja (izrazimo [tex]|y|[/tex] pomoću [tex]|x|[/tex] i ispadne nekakva negativna diskriminanta).
i to je to, skup se može rastaviti na uniju disjunktnih skupova koji su zatvoreni u A, pa nije povezan.
dobro, još je uvjet i da budu neprazni, pa bi bilo zgodno spomenuti da vrijedi npr. [tex](1,0)\in f_1^{-1}(\{0\}), (\frac {1}{2},0) \in f_2^{-1}(\{0\})[/tex]
Added after 9 minutes:
a što se tiče područja diferencijabilnosti, uvijek tražiš najveće moguće otvorene skupove na kojima je očito da je funkcija diferencijabilna.
u ovom slučaju to su:
[tex]\{(x,y) \in R^2: x+y>2\}, \{(x,y) \in R^2: 0<x+y<2\}, \{(x,y)\in R^2: x+y<0\}[/tex]
naravno treba argumentirati zašto su otvoreni i zašto je funkcija diferencijabilna (čisto šablonski)
i onda ispituješ što je sa rubovima tih skupova.
ako si prethodno uspjela dobiti da na nekom od tih rubova funkcija nije neprekidna, onda je to super jer u tim točkama onda ne trebaš ispitivati diferencijabilnost 
|
|
| [Vrh] |
|
angelika
Forumaš(ica)

Pridružen/a: 08. 02. 2011. (17:26:51)
Postovi: (5F)16
|
|
| [Vrh] |
|
an5
Forumaš(ica)
Pridružen/a: 13. 09. 2012. (20:48:55)
Postovi: (9)16
|
|
| [Vrh] |
|
|









