| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
dodgin_lions
Forumaš(ica)

Pridružen/a: 24. 07. 2012. (14:49:47)
Postovi: (22)16
Spol: 
|
|
| [Vrh] |
|
helga
Forumaš(ica)


Pridružen/a: 01. 11. 2011. (22:24:33)
Postovi: (1C)16
Spol: 
|
|
| [Vrh] |
|
matkec
Forumaš(ica)


Pridružen/a: 14. 05. 2010. (16:21:29)
Postovi: (8C)16
|
 Postano: 18:44 uto, 15. 1. 2013 Naslov: Postano: 18:44 uto, 15. 1. 2013 Naslov: |
    |
|
|
2. kolokvij:
1. a)
[latex] \displaystyle \lim_n {\frac{n}{a^{n+1}} ( a+\frac{a^2}{2} + \cdots+ \frac{a^n}{n})} =
\lim_n {\frac{ a+\frac{a^2}{2} + \cdots +\frac{a^n}{n} }{\frac{a^{n+1}}{n}}} [/latex]
Mislim da je sad jasnije na što se lupa Stolz: u brojniku je niz [latex]x_n =a+\frac{a^2}{2} + \cdots +\frac{a^n}{n}[/latex], a nazivniku [latex]y_n=\frac{a^{n+1}}{n}[/latex].
Kad se lupi Stolz i sredi (uzimajući u obzir da je [latex]a[/latex] konstanta, a [latex]n[/latex] varijabla), trebalo bi se dobiti da je limes jednak [latex]\frac{a}{a-1}[/latex].
EDIT: Dobije se [latex]\frac{1}{a-1}[/latex].
1. b)
Tvrdnju dokazujem.
Pretpostavimo suprotno, postoji niz [latex]a_n[/latex] koji nije konvergentan, a da ona tvrdnja vrijedi. Neka su mu [latex]M[/latex] i [latex]m[/latex] limes superior i inferior, redom. Iz pretpostavke slijede da su ta dva broja različita. Definirajmo niz [latex]b_n[/latex] na sljedeći način; [latex]b_n=-a_n[/latex]. Njemu je limes inferior jednak [latex]-M[/latex].
Tvrdnja gore kaže da za svaki niz [latex]b_n[/latex] vrijedi da su limesi inferiori aditivni s nizom [latex]a_n[/latex], pa tako mora vrijediti i za ovaj niz [latex]b_n[/latex], no dobivamo [latex]0=m+(-M)[/latex], što ne vrijedi jer niz [latex]a_n[/latex] nije konvergentan. Kontradikcija.
4. b)
Nažalost, ne znam ga rješiti ovako na prvu loptu, pokušat ću još razmsliti, ali mislim da me L'Hopital razmazio... :P
1. kolokvij:
3. a)
Zadamo funkcije [latex]f_1(x)=ctg \pi x, \ f_2(x)=3^x, \ f_3(x)=-x-x^2[/latex]. Tada je [latex]f = f_3 o f_2 o f_1[/latex].
Da bi f bila injekcija, kao prvo, [latex]f_1[/latex] treba biti injekcija. Ta funkcija je periodična, možemo je restringirati na svakom intervalu oblika [latex]<n,n+1>[/latex], gdje je [latex]n[/latex] cijeli broj. No, dodatni uvjet kaže da je [latex]\frac{5}{2}[/latex] u tom intervalu, dakle, mi moramo uzeti interval [latex]<2,3>[/latex].
Sada trebamo vidjeti dalje trebamo li dalje taj interval smanjivati da bi funkcija bila injekcija no nećemo trebati. Dobivamo da je:
[latex]f_1 : <2,3> \to R, \ f_1(x)=ctg \pi x[/latex] strogo padajuća bijekcija
[latex]f_2 : R \to R^+, \ f_2(x)=3^x[/latex] strogo rastuća bijekcija
[latex]f_3 : R^+ \to R^-, \ f_3(x)=-x-x^2[/latex] strogo padajuća bijekcija
pa je i naša početna funkcija [latex]f[/latex] stogo rastuća bijekcija, dakle injekcija. Traženi interval je <2,3>.
b)
Upravo iz definicija funkcija [latex]f_1,f_2,f_3[/latex] vidimo da je [latex]f(I)=R^-=<-\infty,0>[/latex].
c)
Inverzne funkcije potfunkcija su:
[latex]f_1^{-1} (x)=\frac{arcctg x}{\pi}+2[/latex]
[latex]f_2^{-1} (x)=\log_3 x[/latex]
[latex]f_3^{-1} (x)=\sqrt{\frac{1}{4}-x}-\frac{1}{2}[/latex],
a inverzna od [latex]f[/latex] je [latex]f^{-1}=f_1^{-1}of_2^{-1}of_3^{-1}[/latex]
2. kolokvij:
1. a)
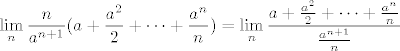
Mislim da je sad jasnije na što se lupa Stolz: u brojniku je niz 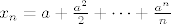 , a nazivniku , a nazivniku 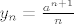 . .
Kad se lupi Stolz i sredi (uzimajući u obzir da je  konstanta, a konstanta, a  varijabla), trebalo bi se dobiti da je limes jednak varijabla), trebalo bi se dobiti da je limes jednak 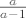 . .
EDIT: Dobije se 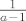 . .
1. b)
Tvrdnju dokazujem.
Pretpostavimo suprotno, postoji niz 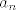 koji nije konvergentan, a da ona tvrdnja vrijedi. Neka su mu koji nije konvergentan, a da ona tvrdnja vrijedi. Neka su mu  i i  limes superior i inferior, redom. Iz pretpostavke slijede da su ta dva broja različita. Definirajmo niz limes superior i inferior, redom. Iz pretpostavke slijede da su ta dva broja različita. Definirajmo niz 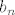 na sljedeći način; na sljedeći način; 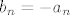 . Njemu je limes inferior jednak . Njemu je limes inferior jednak 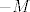 . .
Tvrdnja gore kaže da za svaki niz 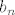 vrijedi da su limesi inferiori aditivni s nizom vrijedi da su limesi inferiori aditivni s nizom 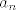 , pa tako mora vrijediti i za ovaj niz , pa tako mora vrijediti i za ovaj niz 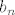 , no dobivamo , no dobivamo  , što ne vrijedi jer niz , što ne vrijedi jer niz 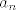 nije konvergentan. Kontradikcija. nije konvergentan. Kontradikcija.
4. b)
Nažalost, ne znam ga rješiti ovako na prvu loptu, pokušat ću još razmsliti, ali mislim da me L'Hopital razmazio... 
1. kolokvij:
3. a)
Zadamo funkcije  . Tada je . Tada je 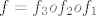 . .
Da bi f bila injekcija, kao prvo, 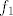 treba biti injekcija. Ta funkcija je periodična, možemo je restringirati na svakom intervalu oblika treba biti injekcija. Ta funkcija je periodična, možemo je restringirati na svakom intervalu oblika 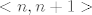 , gdje je , gdje je  cijeli broj. No, dodatni uvjet kaže da je cijeli broj. No, dodatni uvjet kaže da je 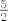 u tom intervalu, dakle, mi moramo uzeti interval u tom intervalu, dakle, mi moramo uzeti interval 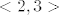 . .
Sada trebamo vidjeti dalje trebamo li dalje taj interval smanjivati da bi funkcija bila injekcija no nećemo trebati. Dobivamo da je:
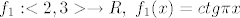 strogo padajuća bijekcija strogo padajuća bijekcija
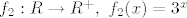 strogo rastuća bijekcija strogo rastuća bijekcija
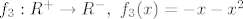 strogo padajuća bijekcija strogo padajuća bijekcija
pa je i naša početna funkcija  stogo rastuća bijekcija, dakle injekcija. Traženi interval je <2,3>. stogo rastuća bijekcija, dakle injekcija. Traženi interval je <2,3>.
b)
Upravo iz definicija funkcija 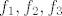 vidimo da je vidimo da je 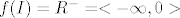 . .
c)
Inverzne funkcije potfunkcija su:
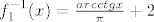
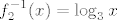
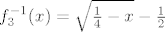 , ,
a inverzna od  je je 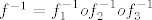
Zadnja promjena: matkec; 19:47 uto, 15. 1. 2013; ukupno mijenjano 1 put.
|
|
| [Vrh] |
|
dodgin_lions
Forumaš(ica)

Pridružen/a: 24. 07. 2012. (14:49:47)
Postovi: (22)16
Spol: 
|
 Postano: 19:33 uto, 15. 1. 2013 Naslov: Postano: 19:33 uto, 15. 1. 2013 Naslov: |
    |
|
|
Hvala puno na trudu.
4.b) sam u međuvremenu saznala kako se rješava. Ako kome bude trebalo, evo hint: uzme se supstitucija arc tg x = y - pi/2, iz toga se izvuče x, upotrijebi formula za oblik 1^besk. i to je to...
EDIT: Također, mislim da je rješenje 1.a) 1/(a-1).
Hvala puno na trudu.
4.b) sam u međuvremenu saznala kako se rješava. Ako kome bude trebalo, evo hint: uzme se supstitucija arc tg x = y - pi/2, iz toga se izvuče x, upotrijebi formula za oblik 1^besk. i to je to...
EDIT: Također, mislim da je rješenje 1.a) 1/(a-1).
Zadnja promjena: dodgin_lions; 19:51 uto, 15. 1. 2013; ukupno mijenjano 1 put.
|
|
| [Vrh] |
|
matkec
Forumaš(ica)


Pridružen/a: 14. 05. 2010. (16:21:29)
Postovi: (8C)16
|
|
| [Vrh] |
|
pingvin007
Forumaš(ica)

Pridružen/a: 28. 10. 2012. (22:20:35)
Postovi: (11)16
|
|
| [Vrh] |
|
dodgin_lions
Forumaš(ica)

Pridružen/a: 24. 07. 2012. (14:49:47)
Postovi: (22)16
Spol: 
|
|
| [Vrh] |
|
alenand
Forumaš(ica)

Pridružen/a: 16. 11. 2011. (21:29:52)
Postovi: (18)16
|
 Postano: 14:35 sri, 16. 1. 2013 Naslov: Postano: 14:35 sri, 16. 1. 2013 Naslov: |
    |
|
|
Što se tiče ovog izraza pod 3. korijenom, radi se tome da:
[dtex]\lim_{x\to0} \frac{1-\cos x}{x^2}=\frac{1}{2}[/dtex]
i analognoj formuli za hiperbolni kosinus:
[dtex]\lim_{x\to0} \frac{\cosh x -1}{x^2}=\frac{1}{2}[/dtex]
Ovo drugu npr. dokažeš pomoću definicije hiperbolnog kosinusa (ono s [tex]e^x[/tex]).
I sad, ak zbrojiš ta dva limesa, dobiješ upravo što treba, naime:
[dtex]\lim_{x\to0} \frac{\cosh x - \cos x} {x^2}=1[/dtex]
Znači početni limes se svodi na:
[dtex]\lim_{x\to0} \frac{e^{2\sin x}\cosh x -1}{x} \cdot \sqrt[3]{\frac{x^2}{\cosh x - \cos x}}[/dtex]
I sad samo treba ovaj prvi dio izračunat, a to napraviš kao što je kolegica iznad rekla - namještavanjem. (Možda se i može malo drugačije moglo doći do tog, ali na kraju bude slično.)
Što se tiče ovog izraza pod 3. korijenom, radi se tome da:
[dtex]\lim_{x\to0} \frac{1-\cos x}{x^2}=\frac{1}{2}[/dtex]
i analognoj formuli za hiperbolni kosinus:
[dtex]\lim_{x\to0} \frac{\cosh x -1}{x^2}=\frac{1}{2}[/dtex]
Ovo drugu npr. dokažeš pomoću definicije hiperbolnog kosinusa (ono s [tex]e^x[/tex]).
I sad, ak zbrojiš ta dva limesa, dobiješ upravo što treba, naime:
[dtex]\lim_{x\to0} \frac{\cosh x - \cos x} {x^2}=1[/dtex]
Znači početni limes se svodi na:
[dtex]\lim_{x\to0} \frac{e^{2\sin x}\cosh x -1}{x} \cdot \sqrt[3]{\frac{x^2}{\cosh x - \cos x}}[/dtex]
I sad samo treba ovaj prvi dio izračunat, a to napraviš kao što je kolegica iznad rekla - namještavanjem. (Možda se i može malo drugačije moglo doći do tog, ali na kraju bude slično.)
|
|
| [Vrh] |
|
Shirohige
Forumaš(ica)

Pridružen/a: 16. 11. 2012. (20:19:56)
Postovi: (ED)16
Spol: 
|
 Postano: 23:44 sri, 16. 1. 2013 Naslov: Postano: 23:44 sri, 16. 1. 2013 Naslov: |
    |
|
|
Molio bih za pomoć s prvim zadatkom pod b)
[url]http://web.math.pmf.unizg.hr/nastava/analiza/kolokviji/ma1-0910-popr.pdf[/url]
Što se tiće b1), je li tu dovoljno se pozivati na neprekidnost i strogi rast pa napisati da je [tex]\displaystyle f([2, 6]) = [f(2), f(6)] = [0, ln2*ln3] [/tex]
?
A b2) sam pokušao i evaluirati sa wolframalphom i nije mi baš pomoglo tj. treba odrediti prasliku na intervalu [-1, 0> pa sam zapisao:
[tex] \displaystyle -1 \le ln\frac{x}{2}ln\frac{x}{3} < 0 [/tex]
Pa mi se činilo da bi mogao f(x) zapisati kao: [tex] \displaystyle (lnx - ln2)(lnx - ln3) = ln^2(x) - ln6lnx + ln2ln3 [/tex]
pa sam napravio supstituciju t = lnx no ta kvadratna jednadžba mi izgleda čudno, jel to uopće ide tako ili sam skroz fulao? :shock:
Molio bih za pomoć s prvim zadatkom pod b)
http://web.math.pmf.unizg.hr/nastava/analiza/kolokviji/ma1-0910-popr.pdf
Što se tiće b1), je li tu dovoljno se pozivati na neprekidnost i strogi rast pa napisati da je [tex]\displaystyle f([2, 6]) = [f(2), f(6)] = [0, ln2*ln3] [/tex]
?
A b2) sam pokušao i evaluirati sa wolframalphom i nije mi baš pomoglo tj. treba odrediti prasliku na intervalu [-1, 0> pa sam zapisao:
[tex] \displaystyle -1 \le ln\frac{x}{2}ln\frac{x}{3} < 0 [/tex]
Pa mi se činilo da bi mogao f(x) zapisati kao: [tex] \displaystyle (lnx - ln2)(lnx - ln3) = ln^2(x) - ln6lnx + ln2ln3 [/tex]
pa sam napravio supstituciju t = lnx no ta kvadratna jednadžba mi izgleda čudno, jel to uopće ide tako ili sam skroz fulao? 
|
|
| [Vrh] |
|
vjekovac
Forumaš(ica)


Pridružen/a: 23. 01. 2003. (18:26:55)
Postovi: (2DB)16
Spol: 
|
 Postano: 11:53 čet, 17. 1. 2013 Naslov: Postano: 11:53 čet, 17. 1. 2013 Naslov: |
    |
|
|
[quote="dodgin_lions"]4.b) sam u međuvremenu saznala kako se rješava. Ako kome bude trebalo, evo hint: uzme se supstitucija arc tg x = y - pi/2, iz toga se izvuče x, upotrijebi formula za oblik 1^besk. i to je to...[/quote]
Evo, napisat cu ovdje rjesenje:
Odmah se vidi da je [tex]\lim_{x\to-\infty}(-\frac{2}{\pi}\mathrm{arctg}x)^{x}[/tex] limes oblika [tex]1^\infty[/tex].
Isto vrijedi i za drugu grupu, nakon sto se korijen zapise kao potencija.
Nakon primjene standardne formule za racunanje limesa tog oblika:
[tex]e^{\lim_{x\to-\infty}x(-\frac{2}{\pi}\mathrm{arctg}x-1)}[/tex]
Sada se supstituira [tex]t=-\frac{2}{\pi}\mathrm{arctg}x-1[/tex], tj.
[tex]x=\mathrm{tg}(-\frac{\pi}{2}(t+1))=\mathrm{ctg}(\frac{\pi}{2}t)=\frac{1}{\mathrm{tg}(\frac{\pi}{2}t)}[/tex]
Kako [tex]t\to 0[/tex], dobili smo limes
[tex]e^{\lim_{t\to 0}t/\mathrm{tg}(\frac{\pi}{2}t)}=e^{2/\pi}[/tex]
[size=9][color=#999999]Added after 20 minutes:[/color][/size]
[quote="Shirohige"]Što se tiće b1), je li tu dovoljno se pozivati na neprekidnost i strogi rast pa napisati da je [tex]\displaystyle f([2, 6]) = [f(2), f(6)] = [0, ln2*ln3] [/tex]?[/quote]
Ustvari f nije rastuca na [2,6].
Cini se da se mora suprstitucijom koju ste napravili (makar su ruzni koeficijenti), odnosno kao kompozicija logaritamske i kvadratne funkcije.
Dobije se [tex][-\frac{1}{4}\ln(\frac{3}{2})^2,\ln 2 \ln 3][/tex]
[quote="Shirohige"]A b2) sam pokušao i evaluirati sa wolframalphom i nije mi baš pomoglo tj. treba odrediti prasliku na intervalu [-1, 0>[/quote]
Dobro ste zapoceli, opet ista supstitucija ili kompozicija.
Dobije se [tex]\langle 2,3\rangle[/tex]
Kad vec koristite Mathematicu / WolframAlpha, mozete si jos vise pomoci skicirajuci graf funkcije. :)
| dodgin_lions (napisa): | | 4.b) sam u međuvremenu saznala kako se rješava. Ako kome bude trebalo, evo hint: uzme se supstitucija arc tg x = y - pi/2, iz toga se izvuče x, upotrijebi formula za oblik 1^besk. i to je to... |
Evo, napisat cu ovdje rjesenje:
Odmah se vidi da je [tex]\lim_{x\to-\infty}(-\frac{2}{\pi}\mathrm{arctg}x)^{x}[/tex] limes oblika [tex]1^\infty[/tex].
Isto vrijedi i za drugu grupu, nakon sto se korijen zapise kao potencija.
Nakon primjene standardne formule za racunanje limesa tog oblika:
[tex]e^{\lim_{x\to-\infty}x(-\frac{2}{\pi}\mathrm{arctg}x-1)}[/tex]
Sada se supstituira [tex]t=-\frac{2}{\pi}\mathrm{arctg}x-1[/tex], tj.
[tex]x=\mathrm{tg}(-\frac{\pi}{2}(t+1))=\mathrm{ctg}(\frac{\pi}{2}t)=\frac{1}{\mathrm{tg}(\frac{\pi}{2}t)}[/tex]
Kako [tex]t\to 0[/tex], dobili smo limes
[tex]e^{\lim_{t\to 0}t/\mathrm{tg}(\frac{\pi}{2}t)}=e^{2/\pi}[/tex]
Added after 20 minutes:
| Shirohige (napisa): | | Što se tiće b1), je li tu dovoljno se pozivati na neprekidnost i strogi rast pa napisati da je [tex]\displaystyle f([2, 6]) = [f(2), f(6)] = [0, ln2*ln3] [/tex]? |
Ustvari f nije rastuca na [2,6].
Cini se da se mora suprstitucijom koju ste napravili (makar su ruzni koeficijenti), odnosno kao kompozicija logaritamske i kvadratne funkcije.
Dobije se [tex][-\frac{1}{4}\ln(\frac{3}{2})^2,\ln 2 \ln 3][/tex]
| Shirohige (napisa): | | A b2) sam pokušao i evaluirati sa wolframalphom i nije mi baš pomoglo tj. treba odrediti prasliku na intervalu [-1, 0> |
Dobro ste zapoceli, opet ista supstitucija ili kompozicija.
Dobije se [tex]\langle 2,3\rangle[/tex]
Kad vec koristite Mathematicu / WolframAlpha, mozete si jos vise pomoci skicirajuci graf funkcije. 
|
|
| [Vrh] |
|
Shirohige
Forumaš(ica)

Pridružen/a: 16. 11. 2012. (20:19:56)
Postovi: (ED)16
Spol: 
|
 Postano: 22:06 čet, 17. 1. 2013 Naslov: Postano: 22:06 čet, 17. 1. 2013 Naslov: |
    |
|
|
[quote="vjekovac"] [quote="Shirohige"]Što se tiće b1), je li tu dovoljno se pozivati na neprekidnost i strogi rast pa napisati da je [tex]\displaystyle f([2, 6]) = [f(2), f(6)] = [0, ln2*ln3] [/tex]?[/quote]
Ustvari f nije rastuca na [2,6].
Cini se da se mora suprstitucijom koju ste napravili (makar su ruzni koeficijenti), odnosno kao kompozicija logaritamske i kvadratne funkcije.
Dobije se [tex][-\frac{1}{4}\ln(\frac{3}{2})^2,\ln 2 \ln 3][/tex]
[quote="Shirohige"]A b2) sam pokušao i evaluirati sa wolframalphom i nije mi baš pomoglo tj. treba odrediti prasliku na intervalu [-1, 0>[/quote]
Dobro ste zapoceli, opet ista supstitucija ili kompozicija.
Dobije se [tex]\langle 2,3\rangle[/tex]
Kad vec koristite Mathematicu / WolframAlpha, mozete si jos vise pomoci skicirajuci graf funkcije. :)[/quote]
Uspio sam dobiti tj. jasno mi je zašto ti intervali, hvala na odgovoru!
Imam još nekoliko pitanja vezane uz zadatke iz 2011/2012 popravni i ovogodišnji prvi kolokvij.
2011/2012 [url]http://web.math.pmf.unizg.hr/nastava/analiza/kolokviji/ma1-1112-pop.pdf[/url]
1. zadatak
odrediti prirodno područje definicije:
[tex] \displaystyle \frac{\sqrt{ln(3-|x|)}}{ln|x|)} - \frac{1}{1 - ch(x^2 + 4x - 5)} [/tex]
I sad redom, ispod korijena mora biti sve veće(ili jednako) od nule tj.
[tex] \displaystyle \sqrt{ln(3-|x|)} \ge 0[/tex]
pa je [tex] \displaystyle x \in <-3, 3>[/tex] jer je ln definiran samo za x-eve veće od 0.
[tex] \displaystyle ln|x| \neq 0 \implies x \neq -1, 1[/tex]
i zadnji [tex] \displaystyle\frac{1}{1 - ch(x^2 + 4x - 5)} \implies ch(x^2 + 4x - 5) \neq 1 \implies x^2 + 4x - 5 \neq 0[/tex] a to vrijedi za [tex] \displaystyle x_1 = 1 \ i\ x_2 = -5[/tex]
pa presjek [tex] \displaystyle x \in <-3, 3> \backslash \{-1, 0, 1\} [/tex]
No wolfram alpha kaže [tex] \displaystyle x \in [-2, 2] \backslash \{-1, 0, 1\} [/tex]:
za input: domain of sqrt(ln(3-|x|))/ln(|x|) - 1/(1-cosh(x^2 + 4x +5))
(ako stavim link, ne prikazuje mi se post)
Gdje griješim?
Pod b)
dobio sam odgovore:
b1) [tex] \displaystyle [ \frac{-2}{3}, 0 > [/tex]
b2) [tex] \displaystyle [ Arcsin \frac{-2}{3}, 0 > [/tex]
Je li to dobro?
2. zadatak
b) Je li f-ja injekcija na intervalu <0, 1>?
Ja bi rekao da je tj. kad se rastavi funkcija na kompozicije, sve su injekcije jedino [tex] \displaystyle x^2 - x [/tex] je upitna no ona ima nultočke u 0 i 1 pa je f-ja na intervalu <0, 1> injekcija ? :shock:
Ovogodišnji kolokvij:
[url]http://web.math.pmf.unizg.hr/nastava/analiza/kolokviji/ma1-1213-kol1.pdf[/url]
3. zadatak, matkec je rješio 3. iz prve grupe (hvala!) pa sam ja pokušao ovog iz druge, pošto je cos periodična funkcija, uzeo sam interval [4, 5] dakle uključujući 4 i 5 pa me zanima je li inverzna funkcija od cos(pi * x) : [tex] \displaystyle x = \frac{arccos(y)}{\pi} + 4 [/tex] ?
I za kraj, 2. zadatak:
[tex] \displaystyle log(\frac{1+sinx}{1-sinx})[/tex]
Uvjet bi očito bio da x nije pi/2 +2k*pi, pošto sin ide of [-1, 1], pa pošto log ima smisla samo za x-eve veće od nula, zato i x ne smije biti 3*pi/2 + 2k*pi no kad promatram vrijednosti blizu -1 i blizu 1 mi se čini da x ide od <0, + beskonačno> , a to log "baca" u R pa bi slika trebala biti R , tako mi se i čini graf na wolframalphi, ali wolframalpha mi ne ispisuje sliku tj. range pa ne znam je li to dobro tj. kako uopće postupiti u tom zadatku. :shock:
Hvala unaprijed na odgovorima!
| vjekovac (napisa): | | Shirohige (napisa): | | Što se tiće b1), je li tu dovoljno se pozivati na neprekidnost i strogi rast pa napisati da je [tex]\displaystyle f([2, 6]) = [f(2), f(6)] = [0, ln2*ln3] [/tex]? |
Ustvari f nije rastuca na [2,6].
Cini se da se mora suprstitucijom koju ste napravili (makar su ruzni koeficijenti), odnosno kao kompozicija logaritamske i kvadratne funkcije.
Dobije se [tex][-\frac{1}{4}\ln(\frac{3}{2})^2,\ln 2 \ln 3][/tex]
| Shirohige (napisa): | | A b2) sam pokušao i evaluirati sa wolframalphom i nije mi baš pomoglo tj. treba odrediti prasliku na intervalu [-1, 0> |
Dobro ste zapoceli, opet ista supstitucija ili kompozicija.
Dobije se [tex]\langle 2,3\rangle[/tex]
Kad vec koristite Mathematicu / WolframAlpha, mozete si jos vise pomoci skicirajuci graf funkcije.  |
Uspio sam dobiti tj. jasno mi je zašto ti intervali, hvala na odgovoru!
Imam još nekoliko pitanja vezane uz zadatke iz 2011/2012 popravni i ovogodišnji prvi kolokvij.
2011/2012 http://web.math.pmf.unizg.hr/nastava/analiza/kolokviji/ma1-1112-pop.pdf
1. zadatak
odrediti prirodno područje definicije:
[tex] \displaystyle \frac{\sqrt{ln(3-|x|)}}{ln|x|)} - \frac{1}{1 - ch(x^2 + 4x - 5)} [/tex]
I sad redom, ispod korijena mora biti sve veće(ili jednako) od nule tj.
[tex] \displaystyle \sqrt{ln(3-|x|)} \ge 0[/tex]
pa je [tex] \displaystyle x \in ←3, 3>[/tex] jer je ln definiran samo za x-eve veće od 0.
[tex] \displaystyle ln|x| \neq 0 \implies x \neq -1, 1[/tex]
i zadnji [tex] \displaystyle\frac{1}{1 - ch(x^2 + 4x - 5)} \implies ch(x^2 + 4x - 5) \neq 1 \implies x^2 + 4x - 5 \neq 0[/tex] a to vrijedi za [tex] \displaystyle x_1 = 1 \ i\ x_2 = -5[/tex]
pa presjek [tex] \displaystyle x \in ←3, 3> \backslash \{-1, 0, 1\} [/tex]
No wolfram alpha kaže [tex] \displaystyle x \in [-2, 2] \backslash \{-1, 0, 1\} [/tex]:
za input: domain of sqrt(ln(3-|x|))/ln(|x|) - 1/(1-cosh(x^2 + 4x +5))
(ako stavim link, ne prikazuje mi se post)
Gdje griješim?
Pod b)
dobio sam odgovore:
b1) [tex] \displaystyle [ \frac{-2}{3}, 0 > [/tex]
b2) [tex] \displaystyle [ Arcsin \frac{-2}{3}, 0 > [/tex]
Je li to dobro?
2. zadatak
b) Je li f-ja injekcija na intervalu <0, 1>?
Ja bi rekao da je tj. kad se rastavi funkcija na kompozicije, sve su injekcije jedino [tex] \displaystyle x^2 - x [/tex] je upitna no ona ima nultočke u 0 i 1 pa je f-ja na intervalu <0, 1> injekcija ? 
Ovogodišnji kolokvij:
http://web.math.pmf.unizg.hr/nastava/analiza/kolokviji/ma1-1213-kol1.pdf
3. zadatak, matkec je rješio 3. iz prve grupe (hvala!) pa sam ja pokušao ovog iz druge, pošto je cos periodična funkcija, uzeo sam interval [4, 5] dakle uključujući 4 i 5 pa me zanima je li inverzna funkcija od cos(pi * x) : [tex] \displaystyle x = \frac{arccos(y)}{\pi} + 4 [/tex] ?
I za kraj, 2. zadatak:
[tex] \displaystyle log(\frac{1+sinx}{1-sinx})[/tex]
Uvjet bi očito bio da x nije pi/2 +2k*pi, pošto sin ide of [-1, 1], pa pošto log ima smisla samo za x-eve veće od nula, zato i x ne smije biti 3*pi/2 + 2k*pi no kad promatram vrijednosti blizu -1 i blizu 1 mi se čini da x ide od <0, + beskonačno> , a to log "baca" u R pa bi slika trebala biti R , tako mi se i čini graf na wolframalphi, ali wolframalpha mi ne ispisuje sliku tj. range pa ne znam je li to dobro tj. kako uopće postupiti u tom zadatku. 
Hvala unaprijed na odgovorima!
Zadnja promjena: Shirohige; 17:49 pet, 18. 1. 2013; ukupno mijenjano 1 put.
|
|
| [Vrh] |
|
El_Loco
Forumaš(ica)

Pridružen/a: 26. 05. 2012. (15:25:04)
Postovi: (31)16
Spol: 
|
|
| [Vrh] |
|
Shirohige
Forumaš(ica)

Pridružen/a: 16. 11. 2012. (20:19:56)
Postovi: (ED)16
Spol: 
|
|
| [Vrh] |
|
dodgin_lions
Forumaš(ica)

Pridružen/a: 24. 07. 2012. (14:49:47)
Postovi: (22)16
Spol: 
|
 Postano: 14:56 pet, 18. 1. 2013 Naslov: Postano: 14:56 pet, 18. 1. 2013 Naslov: |
    |
|
|
[quote="Shirohige"]No wolfram alpha kaže [tex] \displaystyle x \in [-2, 2] \backslash \{-1, 0, 1\} [/tex]:[/quote]
Meni ispada \{-1,0,1,-5}, jer su nul-točke od x^2+4x-5 1 i -5. Zašto tu onda nema -5? :?
EDIT: zar nije 1.b1)
[-pi/2, pi/2> ?
| Shirohige (napisa): | | No wolfram alpha kaže [tex] \displaystyle x \in [-2, 2] \backslash \{-1, 0, 1\} [/tex]: |
Meni ispada \{-1,0,1,-5}, jer su nul-točke od x^2+4x-5 1 i -5. Zašto tu onda nema -5? 
EDIT: zar nije 1.b1)
[-pi/2, pi/2> ?
|
|
| [Vrh] |
|
dodgin_lions
Forumaš(ica)

Pridružen/a: 24. 07. 2012. (14:49:47)
Postovi: (22)16
Spol: 
|
|
| [Vrh] |
|
Shirohige
Forumaš(ica)

Pridružen/a: 16. 11. 2012. (20:19:56)
Postovi: (ED)16
Spol: 
|
 Postano: 17:58 pet, 18. 1. 2013 Naslov: Postano: 17:58 pet, 18. 1. 2013 Naslov: |
    |
|
|
[quote="dodgin_lions"][quote="Shirohige"]No wolfram alpha kaže [tex] \displaystyle x \in [-2, 2] \backslash \{-1, 0, 1\} [/tex]:[/quote]
Meni ispada \{-1,0,1,-5}, jer su nul-točke od x^2+4x-5 1 i -5. Zašto tu onda nema -5? :?
EDIT: zar nije 1.b1)
[-pi/2, pi/2> ?[/quote]
Nema potrebe pisati -5 jer ti je gl. interval [-2, 2] pa te zanimaju samo "nepravilne" vrijednosti unutar tog intervala, a to su -1, 0 i 1.
A što se b tiće, pa f([-pi/2, pi/2>) baca sliku na [-2/3, 0 > pa sam stavio [Arcsin(-2/3), 0> pošto je Arcsin na tom intervalu definiran.
[quote]Također, 2.b) ne bi trebala bit injekcija jer x^2-x nije injekcija od 0 do 1 (vidi se iz skice ).[/quote]
Točno! hvala
| dodgin_lions (napisa): | | Shirohige (napisa): | | No wolfram alpha kaže [tex] \displaystyle x \in [-2, 2] \backslash \{-1, 0, 1\} [/tex]: |
Meni ispada \{-1,0,1,-5}, jer su nul-točke od x^2+4x-5 1 i -5. Zašto tu onda nema -5? 
EDIT: zar nije 1.b1)
[-pi/2, pi/2> ? |
Nema potrebe pisati -5 jer ti je gl. interval [-2, 2] pa te zanimaju samo "nepravilne" vrijednosti unutar tog intervala, a to su -1, 0 i 1.
A što se b tiće, pa f([-pi/2, pi/2>) baca sliku na [-2/3, 0 > pa sam stavio [Arcsin(-2/3), 0> pošto je Arcsin na tom intervalu definiran.
| Citat: | | Također, 2.b) ne bi trebala bit injekcija jer x^2-x nije injekcija od 0 do 1 (vidi se iz skice ). |
Točno! hvala
|
|
| [Vrh] |
|
dodgin_lions
Forumaš(ica)

Pridružen/a: 24. 07. 2012. (14:49:47)
Postovi: (22)16
Spol: 
|
 Postano: 18:40 pet, 18. 1. 2013 Naslov: Postano: 18:40 pet, 18. 1. 2013 Naslov: |
    |
|
|
[quote="Shirohige"]
A što se b tiće, pa f([-pi/2, pi/2>) baca sliku na [-2/3, 0 > pa sam stavio [Arcsin(-2/3), 0> pošto je Arcsin na tom intervalu definiran.
[/quote]
Hm. Zar nije f^-1 praslika, dakle traži se praslika od intervala [-2/3,0]? Ako to tražim, kompozicijama, dobijem drugačije...
| Shirohige (napisa): |
A što se b tiće, pa f([-pi/2, pi/2>) baca sliku na [-2/3, 0 > pa sam stavio [Arcsin(-2/3), 0> pošto je Arcsin na tom intervalu definiran.
|
Hm. Zar nije f^-1 praslika, dakle traži se praslika od intervala [-2/3,0]? Ako to tražim, kompozicijama, dobijem drugačije...
|
|
| [Vrh] |
|
Shirohige
Forumaš(ica)

Pridružen/a: 16. 11. 2012. (20:19:56)
Postovi: (ED)16
Spol: 
|
 Postano: 21:23 pet, 18. 1. 2013 Naslov: Postano: 21:23 pet, 18. 1. 2013 Naslov: |
    |
|
|
[quote="dodgin_lions"][quote="Shirohige"]
A što se b tiće, pa f([-pi/2, pi/2>) baca sliku na [-2/3, 0 > pa sam stavio [Arcsin(-2/3), 0> pošto je Arcsin na tom intervalu definiran.
[/quote]
Hm. Zar nije f^-1 praslika, dakle traži se praslika od intervala [-2/3,0]? Ako to tražim, kompozicijama, dobijem drugačije...[/quote]
Ovako?
[tex] \displaystyle f(x) = \frac{sin(x) - 1}{2 - sin(x)} \\[0.5cm]
\displaystyle f = f_2(f_1(x)) \\
\displaystyle f_1 = sinx; \\
\displaystyle f_2 = \frac{x-1}{2-x} \\[0.5cm]
\displaystyle f_2 (f_1 ([\frac{-\pi}{2} , \frac{\pi}{2}>)) = f_2([-1, 1>) = [\frac{-2}{3} , 0 >) \\ \\[0.5cm]
\displaystyle f^{-1}(f([\frac{-\pi}{2} , \frac{\pi}{2}>)) = f_1^{-1}(f_2^{-1}([\frac{-2}{3} , 0 >)) = f_1^{-1}([-1, 1>) = [\frac{-\pi}{2} , \frac{\pi}{2}>
[/tex]
edit [tex] \displaystyle f_1^{-1}([-1, 1>) = [\frac{-\pi}{2} + 2k\pi , \frac{\pi}{2} + 2k\pi > \ \ k\in\mathbb{Z} [/tex]
| dodgin_lions (napisa): | | Shirohige (napisa): |
A što se b tiće, pa f([-pi/2, pi/2>) baca sliku na [-2/3, 0 > pa sam stavio [Arcsin(-2/3), 0> pošto je Arcsin na tom intervalu definiran.
|
Hm. Zar nije f^-1 praslika, dakle traži se praslika od intervala [-2/3,0]? Ako to tražim, kompozicijama, dobijem drugačije... |
Ovako?
[tex] \displaystyle f(x) = \frac{sin(x) - 1}{2 - sin(x)} \\[0.5cm]
\displaystyle f = f_2(f_1(x)) \\
\displaystyle f_1 = sinx; \\
\displaystyle f_2 = \frac{x-1}{2-x} \\[0.5cm]
\displaystyle f_2 (f_1 ([\frac{-\pi}{2} , \frac{\pi}{2}>)) = f_2([-1, 1>) = [\frac{-2}{3} , 0 >) \\ \\[0.5cm]
\displaystyle f^{-1}(f([\frac{-\pi}{2} , \frac{\pi}{2}>)) = f_1^{-1}(f_2^{-1}([\frac{-2}{3} , 0 >)) = f_1^{-1}([-1, 1>) = [\frac{-\pi}{2} , \frac{\pi}{2}>
[/tex]
edit [tex] \displaystyle f_1^{-1}([-1, 1>) = [\frac{-\pi}{2} + 2k\pi , \frac{\pi}{2} + 2k\pi > \ \ k\in\mathbb{Z} [/tex]
Zadnja promjena: Shirohige; 11:52 sub, 19. 1. 2013; ukupno mijenjano 1 put.
|
|
| [Vrh] |
|
dodgin_lions
Forumaš(ica)

Pridružen/a: 24. 07. 2012. (14:49:47)
Postovi: (22)16
Spol: 
|
|
| [Vrh] |
|
54321
Forumaš(ica)

Pridružen/a: 19. 01. 2013. (14:12:37)
Postovi: (1)16
|
|
| [Vrh] |
|
|



















