| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
pedro
Forumaš(ica)
Pridružen/a: 21. 10. 2010. (14:08:21)
Postovi: (19B)16
|
 Postano: 22:52 sub, 19. 1. 2013 Naslov: |
    |
|
|
[quote="nuclear"]http://web.math.pmf.unizg.hr/nastava/difraf/dif/2009-10/zavrsni.pdf
1. zadatak, pod a)
Je li ovo dovoljno dobro objašnjenje? Nekako, svaki put kad idem nešto dokazivati, izgubim pola bodova a ne znam gdje griješim.. :
definiramo funkciju [latex]f: R^3->R f(x,y,z)=x^2+3y^2-6[/latex]
Funkcija f je neprekidna funkcija kao zbroj, umnožak neprekidnih funkcija i projekcije:
[latex]p_1:R^3->R[/latex] [latex]p_1(x,y,z)=x[/latex]
[latex]p_2:R^3->R[/latex] [latex]p_2(x,y,z)=y[/latex]
[latex]g_1:R->R[/latex] [latex]g_1(x)=x^2[/latex]
[latex]f=g_1(p_1) + 3g_1(p_2) -6[/latex]
nadalje, jer je funkcija neprekidna, i vrijedi da je [latex]f<=0[/latex], odnosno slika funkcije f je (ne znam baš sve u lateksu) <-besk, 0] je zatvoren skup, pa je i njena praslika zatvoren skup, odnosno A=praslika(tntn..) je zatvoren skup.
[size=9][color=#999999]Added after 29 minutes:[/color][/size]
http://web.math.pmf.unizg.hr/nastava/difraf/dif/2009-10/zavrsni.pdf
čini mi se da krivo deriviram :D
2. zadatak:
računah derivaciju od f po [latex]x_j[/latex]:
[latex]1/(||x||^2) 2x_j cos( a_1x_1+...a_nx_n) - ln(||x||^2)sin(a_1x_1+...a_nx_n)a [/latex]
ovih tjedan dana prođe i zaboravih derivirati :shell:[/quote]
čini mi se da ti je dobro derivirano. tako sam nekak i ja dobila
ak dobiješ rj
[sqrt2 0...0]
onda ti je sigurno točno :D
[size=9][color=#999999]Added after 29 minutes:[/color][/size]
[quote="Loo"][quote="angelika"]http://web.math.pmf.unizg.hr/nastava/difraf/z2009.pdf
može mala pomoć sa 2.zadatkom? Kako da odredim područje diferencijabilnosti?
i kako u 1.zad provjeriti da li je skup povezan?[/quote]
1. skup je povezan ako se ne može rastaviti na uniju dva neprazna disjunktna skupa koji su otvoreni/zatvoreni u tom skupu.
s obzirom na to kako je skup zadan, možemo pokušati vidjeti koje će to točke biti u tom skupu.
vrijedit će
[tex](|x|+|y|-1)(x^2+y^2-\frac {1}{4})=0[/tex]
akko
[tex]|x|+|y|-1=0[/tex] ili [tex]x^2+y^2-\frac {1}{4}=0[/tex]
dakle ako definiramo funkcije
[tex]f_1(x,y)=|x|+|y|-1, f_2(x,y)=x^2+y^2-\frac {1}{4}[/tex] tada će vrijediti [tex]A=f_1^{-1}(\{0\})\cup f_2^{-1}(\{0\})[/tex]
funkcije su neprekidne, [tex]\{0\}[/tex] je zatvoren, pa su ove dvije praslike zatvoreni skupovi.
sada bi bilo super kada bi uspjeli dokazati da su te dvije praslike disjunktne jer tada [tex]A[/tex] nije povezan.
rješavamo sustav jer za točke u presjeku moraju vrijediti obje jednakosti:
[tex]|x|+|y|-1=0[/tex]
[tex]x^2+y^2-\frac {1}{4}=0[/tex]
te vidimo da ovaj sustav nema rješenja (izrazimo [tex]|y|[/tex] pomoću [tex]|x|[/tex] i ispadne nekakva negativna diskriminanta).
i to je to, skup se može rastaviti na uniju disjunktnih skupova koji su zatvoreni u A, pa nije povezan.
dobro, još je uvjet i da budu neprazni, pa bi bilo zgodno spomenuti da vrijedi npr. [tex](1,0)\in f_1^{-1}(\{0\}), (\frac {1}{2},0) \in f_2^{-1}(\{0\})[/tex]
[/quote]
može sustav malo detaljnije
| nuclear (napisa): | http://web.math.pmf.unizg.hr/nastava/difraf/dif/2009-10/zavrsni.pdf
1. zadatak, pod a)
Je li ovo dovoljno dobro objašnjenje? Nekako, svaki put kad idem nešto dokazivati, izgubim pola bodova a ne znam gdje griješim.. :
definiramo funkciju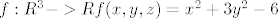 
Funkcija f je neprekidna funkcija kao zbroj, umnožak neprekidnih funkcija i projekcije:
 
 
 
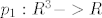
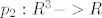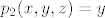
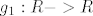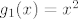
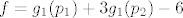
nadalje, jer je funkcija neprekidna, i vrijedi da je 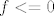 , odnosno slika funkcije f je (ne znam baš sve u lateksu) ←besk, 0] je zatvoren skup, pa je i njena praslika zatvoren skup, odnosno A=praslika(tntn..) je zatvoren skup.
Added after 29 minutes:
http://web.math.pmf.unizg.hr/nastava/difraf/dif/2009-10/zavrsni.pdf
čini mi se da krivo deriviram 
2. zadatak:
računah derivaciju od f po  :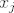
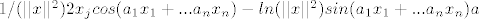
ovih tjedan dana prođe i zaboravih derivirati  |
čini mi se da ti je dobro derivirano. tako sam nekak i ja dobila
ak dobiješ rj
[sqrt2 0...0]
onda ti je sigurno točno
Added after 29 minutes:
| Loo (napisa): | | angelika (napisa): | http://web.math.pmf.unizg.hr/nastava/difraf/z2009.pdf
može mala pomoć sa 2.zadatkom? Kako da odredim područje diferencijabilnosti?
i kako u 1.zad provjeriti da li je skup povezan? |
1. skup je povezan ako se ne može rastaviti na uniju dva neprazna disjunktna skupa koji su otvoreni/zatvoreni u tom skupu.
s obzirom na to kako je skup zadan, možemo pokušati vidjeti koje će to točke biti u tom skupu.
vrijedit će
[tex](|x|+|y|-1)(x^2+y^2-\frac {1}{4})=0[/tex]
akko
[tex]|x|+|y|-1=0[/tex] ili [tex]x^2+y^2-\frac {1}{4}=0[/tex]
dakle ako definiramo funkcije
[tex]f_1(x,y)=|x|+|y|-1, f_2(x,y)=x^2+y^2-\frac {1}{4}[/tex] tada će vrijediti [tex]A=f_1^{-1}(\{0\})\cup f_2^{-1}(\{0\})[/tex]
funkcije su neprekidne, [tex]\{0\}[/tex] je zatvoren, pa su ove dvije praslike zatvoreni skupovi.
sada bi bilo super kada bi uspjeli dokazati da su te dvije praslike disjunktne jer tada [tex]A[/tex] nije povezan.
rješavamo sustav jer za točke u presjeku moraju vrijediti obje jednakosti:
[tex]|x|+|y|-1=0[/tex]
[tex]x^2+y^2-\frac {1}{4}=0[/tex]
te vidimo da ovaj sustav nema rješenja (izrazimo [tex]|y|[/tex] pomoću [tex]|x|[/tex] i ispadne nekakva negativna diskriminanta).
i to je to, skup se može rastaviti na uniju disjunktnih skupova koji su zatvoreni u A, pa nije povezan.
dobro, još je uvjet i da budu neprazni, pa bi bilo zgodno spomenuti da vrijedi npr. [tex](1,0)\in f_1^{-1}(\{0\}), (\frac {1}{2},0) \in f_2^{-1}(\{0\})[/tex]
|
može sustav malo detaljnije
|
|
| [Vrh] |
|
aptx
Forumaš(ica)
Pridružen/a: 11. 01. 2013. (00:15:01)
Postovi: (15)16
|
|
| [Vrh] |
|
pedro
Forumaš(ica)
Pridružen/a: 21. 10. 2010. (14:08:21)
Postovi: (19B)16
|
| Postano: 9:36 ned, 20. 1. 2013 Naslov: |
|
|
|
[quote="aptx"]http://web.math.pmf.unizg.hr/nastava/difraf/dif/2010-11/zavrsni.pdf
1.zad kako omeđiti funkciju i je li S otvoren? :/[/quote]
hm ja bi svaki e^x^2<=2 i tako za y^2 i z^2
onda dobijem x^2<=ln2 abs(x)<=sqrt(ln2)
analogno za y^2 i z^2.
neka me netko ispravi ako nije dobro
[size=9][color=#999999]Added after 6 minutes:[/color][/size]
[quote="aptx"]http://web.math.pmf.unizg.hr/nastava/difraf/dif/2010-11/zavrsni.pdf
1.zad kako omeđiti funkciju i je li S otvoren? :/[/quote]
može drugi? mogu li ić pokazivati diferencijabilnost u svakoj točki jer će to povlačit neprekidnost?
pa posebno gledam za točke gdje je y >0, y<0 i y=0?? jel onda moram gledati točke oblika (x,0) ili moram i (0,0), mislim da trebam za (x,0) jer ne vidim da igdje smeta x=0?
| aptx (napisa): | http://web.math.pmf.unizg.hr/nastava/difraf/dif/2010-11/zavrsni.pdf
1.zad kako omeđiti funkciju i je li S otvoren?  |
hm ja bi svaki e^x^2⇐2 i tako za y^2 i z^2
onda dobijem x^2⇐ln2 abs(x)⇐sqrt(ln2)
analogno za y^2 i z^2.
neka me netko ispravi ako nije dobro
Added after 6 minutes:
| aptx (napisa): | http://web.math.pmf.unizg.hr/nastava/difraf/dif/2010-11/zavrsni.pdf
1.zad kako omeđiti funkciju i je li S otvoren? |
može drugi? mogu li ić pokazivati diferencijabilnost u svakoj točki jer će to povlačit neprekidnost?
pa posebno gledam za točke gdje je y >0, y<0 i y=0?? jel onda moram gledati točke oblika (x,0) ili moram i (0,0), mislim da trebam za (x,0) jer ne vidim da igdje smeta x=0?
|
|
| [Vrh] |
|
Phoenix
Forumaš(ica)
Pridružen/a: 15. 05. 2010. (18:46:07)
Postovi: (164)16
Sarma: -
|
| Postano: 9:50 ned, 20. 1. 2013 Naslov: |
|
|
|
pedro, ja te neću ispravljati jer si dobro raspisala. Bravo! :D
Što se tiče 2. zadatka, ja bih postupio na obrnuti način: gledao bih neprekidnost pa, ako funkcija u nekoj točki nije neprekidna, tu ne moram provjeravati diferencijabilnost. Zatim u preostalim točkama provjeravam diferencijabilnost funkcije. :)
Vjerujem da i ovo tvoje pali, no za ovaj zadatak mi se drugi smjer dokazivanja čini bolji. :)
pedro, ja te neću ispravljati jer si dobro raspisala. Bravo!
Što se tiče 2. zadatka, ja bih postupio na obrnuti način: gledao bih neprekidnost pa, ako funkcija u nekoj točki nije neprekidna, tu ne moram provjeravati diferencijabilnost. Zatim u preostalim točkama provjeravam diferencijabilnost funkcije. 
Vjerujem da i ovo tvoje pali, no za ovaj zadatak mi se drugi smjer dokazivanja čini bolji.
|
|
| [Vrh] |
|
pedro
Forumaš(ica)
Pridružen/a: 21. 10. 2010. (14:08:21)
Postovi: (19B)16
|
| Postano: 10:17 ned, 20. 1. 2013 Naslov: |
|
|
|
[quote="Phoenix"]pedro, ja te neću ispravljati jer si dobro raspisala. Bravo! :D
[/quote]
ajde super da sam i ja nekom pomogla :) A za otvorenost ako možeš dat neku ideju jer fkt nebih znala
[quote]
Što se tiče 2. zadatka, ja bih postupio na obrnuti način: gledao bih neprekidnost pa, ako funkcija u nekoj točki nije neprekidna, tu ne moram provjeravati diferencijabilnost. Zatim u preostalim točkama provjeravam diferencijabilnost funkcije. :)
Vjerujem da i ovo tvoje pali, no za ovaj zadatak mi se drugi smjer dokazivanja čini bolji. :[/quote]
hm, al trebamo pokazati da funkcija je dfb, ako bi prvo pokazivali neprekidnost nebi li onda radili više posla, jer onda dodatno moramo pokazivati diferencijabilnost. ovo bi radila u slučaju da funkcija nije dfb?
i jel to provjeravamo za točke oblika (x,y),y<0 (x,y),y>0 i (x,0) ???
[size=9][color=#999999]Added after 22 minutes:[/color][/size]
hm, mislim da sam shvatila zašto prvo neprekidnost.
jer možemo u ovom slučaju odmah za točke oblika (x,y),y>0 i (x,y),y<0 reći da su neprekidne radi kvocjenta, umnoška,razlike projekcija(odmah možemo to reć i za diferencijabilnost)?
i samo provjeravamo za y=0?
| Phoenix (napisa): | pedro, ja te neću ispravljati jer si dobro raspisala. Bravo!
|
ajde super da sam i ja nekom pomogla A za otvorenost ako možeš dat neku ideju jer fkt nebih znala
| Citat: |
Što se tiče 2. zadatka, ja bih postupio na obrnuti način: gledao bih neprekidnost pa, ako funkcija u nekoj točki nije neprekidna, tu ne moram provjeravati diferencijabilnost. Zatim u preostalim točkama provjeravam diferencijabilnost funkcije.
Vjerujem da i ovo tvoje pali, no za ovaj zadatak mi se drugi smjer dokazivanja čini bolji. : |
hm, al trebamo pokazati da funkcija je dfb, ako bi prvo pokazivali neprekidnost nebi li onda radili više posla, jer onda dodatno moramo pokazivati diferencijabilnost. ovo bi radila u slučaju da funkcija nije dfb?
i jel to provjeravamo za točke oblika (x,y),y<0 (x,y),y>0 i (x,0) ???
Added after 22 minutes:
hm, mislim da sam shvatila zašto prvo neprekidnost.
jer možemo u ovom slučaju odmah za točke oblika (x,y),y>0 i (x,y),y<0 reći da su neprekidne radi kvocjenta, umnoška,razlike projekcija(odmah možemo to reć i za diferencijabilnost)?
i samo provjeravamo za y=0?
|
|
| [Vrh] |
|
mata
Forumaš(ica)
Pridružen/a: 02. 04. 2011. (17:50:57)
Postovi: (17)16
|
|
| [Vrh] |
|
pedro
Forumaš(ica)
Pridružen/a: 21. 10. 2010. (14:08:21)
Postovi: (19B)16
|
| Postano: 15:15 ned, 20. 1. 2013 Naslov: |
|
|
|
[quote="aptx"]http://web.math.pmf.unizg.hr/nastava/difraf/dif/2010-11/zavrsni.pdf
1.zad kako omeđiti funkciju i je li S otvoren? :/[/quote]
ovako sam ja došla do zaključka da nije otvoren
postoje neki skupovi koji su i otvoreni i zatvoreni, kao prazan skup i R^n, da bi S bio otvoren trebao bi bit definiran na cijelom R^2 ali nije. sad, koliko je to točno, ja fkt ne znam
[size=9][color=#999999]Added after 4 minutes:[/color][/size]
[quote="mata"]
[size=9][color=#999999]Added after 33 minutes:[/color][/size]
http://web.math.pmf.unizg.hr/nastava/difraf/dif/2012-13/kolokvij2.pdf
Jel moze pliz pomoc s 2.b)?[/quote]
ja sam ti na tom zad dobila 15 bodova, mislim da mi je pod a) cijeli točan tako da sam negdje u b) zeznula, al evo kako sam išla
ugl. xy ravnina ti je definirana funkcijom z=0
sada izračunaš normalu od one zadane funkcije i normalu od z=0
i one moraju biti paralelne, tj dokazat to moraš
ja sam dobila(0,0,1)= lambda* (0,0,1)
i vidimo da su paralelne za svaki lambda. I sad bi molila dobru dušu da to još nadopuni i ispravi što sam krivo napravila :)
[size=9][color=#999999]Added after 9 minutes:[/color][/size]
http://web.math.pmf.unizg.hr/nastava/difraf/dif/2012-13/kolokvij1.pdf
može 1. i 4?
| aptx (napisa): | http://web.math.pmf.unizg.hr/nastava/difraf/dif/2010-11/zavrsni.pdf
1.zad kako omeđiti funkciju i je li S otvoren? |
ovako sam ja došla do zaključka da nije otvoren
postoje neki skupovi koji su i otvoreni i zatvoreni, kao prazan skup i R^n, da bi S bio otvoren trebao bi bit definiran na cijelom R^2 ali nije. sad, koliko je to točno, ja fkt ne znam
Added after 4 minutes:
ja sam ti na tom zad dobila 15 bodova, mislim da mi je pod a) cijeli točan tako da sam negdje u b) zeznula, al evo kako sam išla
ugl. xy ravnina ti je definirana funkcijom z=0
sada izračunaš normalu od one zadane funkcije i normalu od z=0
i one moraju biti paralelne, tj dokazat to moraš
ja sam dobila(0,0,1)= lambda* (0,0,1)
i vidimo da su paralelne za svaki lambda. I sad bi molila dobru dušu da to još nadopuni i ispravi što sam krivo napravila
Added after 9 minutes:
http://web.math.pmf.unizg.hr/nastava/difraf/dif/2012-13/kolokvij1.pdf
može 1. i 4?
|
|
| [Vrh] |
|
an5
Forumaš(ica)
Pridružen/a: 13. 09. 2012. (20:48:55)
Postovi: (9)16
|
| Postano: 16:43 ned, 20. 1. 2013 Naslov: |
|
|
|
za 4. a) i b) bi ja rekla ovako otprilike (neka me netko ispravi ako je krivo)
a) f(x,y)=xy je neprekidna funkcija (kao produkt neprekidnih funkcija)
f:[-1,1]x[-1,1] - R , vidimo da je domena kompaktan skup, odnosno mozemo to zapisati kao S={(x,y) e R^2 : -1<=x<=1, -1<=y<=1} i vidimo da je S ograničen i zatvoren i po teoremu s predavanja vrijedi da ako je skup kompaktan i f neprekidna tada je f ogranicena i postize minimum i maksimum ...
pod b) analogno, ako izbacimo {(0,0)} i dalje je domena kompaktan skup
za 4. a) i b) bi ja rekla ovako otprilike (neka me netko ispravi ako je krivo)
a) f(x,y)=xy je neprekidna funkcija (kao produkt neprekidnih funkcija)
f:[-1,1]x[-1,1] - R , vidimo da je domena kompaktan skup, odnosno mozemo to zapisati kao S={(x,y) e R^2 : -1⇐x⇐1, -1⇐y⇐1} i vidimo da je S ograničen i zatvoren i po teoremu s predavanja vrijedi da ako je skup kompaktan i f neprekidna tada je f ogranicena i postize minimum i maksimum ...
pod b) analogno, ako izbacimo {(0,0)} i dalje je domena kompaktan skup
|
|
| [Vrh] |
|
pedro
Forumaš(ica)
Pridružen/a: 21. 10. 2010. (14:08:21)
Postovi: (19B)16
|
| Postano: 16:46 ned, 20. 1. 2013 Naslov: |
|
|
|
[quote="an5"]za 4. a) i b) bi ja rekla ovako otprilike (neka me netko ispravi ako je krivo)
a) f(x,y)=xy je neprekidna funkcija (kao produkt neprekidnih funkcija)
f:[-1,1]x[-1,1] - R , vidimo da je domena kompaktan skup, odnosno mozemo to zapisati kao S={(x,y) e R^2 : -1<=x<=1, -1<=y<=1} i vidimo da je S ograničen i zatvoren i po teoremu s predavanja vrijedi da ako je skup kompaktan i f neprekidna tada je f ogranicena i postize minimum i maksimum ...
pod b) analogno, ako izbacimo {(0,0)} i dalje je domena kompaktan skup[/quote]
meni se čini da b) nije ni zatvoren ni otvoren :/ ne znam
| an5 (napisa): | za 4. a) i b) bi ja rekla ovako otprilike (neka me netko ispravi ako je krivo)
a) f(x,y)=xy je neprekidna funkcija (kao produkt neprekidnih funkcija)
f:[-1,1]x[-1,1] - R , vidimo da je domena kompaktan skup, odnosno mozemo to zapisati kao S={(x,y) e R^2 : -1⇐x⇐1, -1⇐y⇐1} i vidimo da je S ograničen i zatvoren i po teoremu s predavanja vrijedi da ako je skup kompaktan i f neprekidna tada je f ogranicena i postize minimum i maksimum ...
pod b) analogno, ako izbacimo {(0,0)} i dalje je domena kompaktan skup |
meni se čini da b) nije ni zatvoren ni otvoren ne znam
|
|
| [Vrh] |
|
frutabella
Forumaš(ica)
Pridružen/a: 09. 10. 2010. (16:35:36)
Postovi: (24E)16
|
| Postano: 21:24 ned, 20. 1. 2013 Naslov: |
|
|
|
[quote="pedro"]
-sqrt6 <= x <= sqrt6
-sqrt2 <= y <= sqrt2
0 <= z <= 2
[/quote]
Zar ne bi trebalo z ograniciti između -2 i 2?
I moze li malo detaljnije zadatak 2 (znaci sa zavrsenog 2010.)
Hvala
:oops: Vidjela sam gore da je rjeseno Df(1,0...0),
domena je valjda Df=R\<-besk, 0]; Df'=R
Ovo da je diferencijabilna u svim tockama treba dokazati po definiciji?
[size=9][color=#999999]Added after 43 minutes:[/color][/size]
http://web.math.pmf.unizg.hr/nastava/difraf/dif/2009-10/zavrsni.pdf
3. zad pod b)
Oznacila sam S={ (x,y): x^2+y^2-4=0}; f(x,y)=xy (povrsina)
Preko teorema o uvjetnim eksretmima dobivam:
kandidate za tocke ekstreme
(sqrt(2),sqrt(2)) i (-sqrt(2),-sqrt(2))
f od ova dva kandidata je je 2.
Da li je ovo ok?
| pedro (napisa): |
-sqrt6 ⇐ x ⇐ sqrt6
-sqrt2 ⇐ y ⇐ sqrt2
0 ⇐ z ⇐ 2
|
Zar ne bi trebalo z ograniciti između -2 i 2?
I moze li malo detaljnije zadatak 2 (znaci sa zavrsenog 2010.)
Hvala
 Vidjela sam gore da je rjeseno Df(1,0...0),
domena je valjda Df=R\←besk, 0]; Df'=R
Ovo da je diferencijabilna u svim tockama treba dokazati po definiciji?
Added after 43 minutes:
http://web.math.pmf.unizg.hr/nastava/difraf/dif/2009-10/zavrsni.pdf
3. zad pod b)
Oznacila sam S={ (x,y): x^2+y^2-4=0}; f(x,y)=xy (povrsina)
Preko teorema o uvjetnim eksretmima dobivam:
kandidate za tocke ekstreme
(sqrt(2),sqrt(2)) i (-sqrt(2),-sqrt(2))
f od ova dva kandidata je je 2.
Da li je ovo ok?
|
|
| [Vrh] |
|
pedro
Forumaš(ica)
Pridružen/a: 21. 10. 2010. (14:08:21)
Postovi: (19B)16
|
| Postano: 21:32 ned, 20. 1. 2013 Naslov: |
|
|
|
[quote="frutabella"][quote="pedro"]
-sqrt6 <= x <= sqrt6
-sqrt2 <= y <= sqrt2
0 <= z <= 2
[/quote]
Zar ne bi trebalo z ograniciti između -2 i 2?
I moze li malo detaljnije zadatak 2 (znaci sa zavrsenog 2010.)
Hvala
:oops: Vidjela sam gore da je rjeseno Df(1,0...0),
domena je valjda Df=R\<-besk, 0]; Df'=R
Ovo da je diferencijabilna u svim tockama treba dokazati po definiciji?
[size=9][color=#999999]Added after 43 minutes:[/color][/size]
http://web.math.pmf.unizg.hr/nastava/difraf/dif/2009-10/zavrsni.pdf
3. zad pod b)
Oznacila sam S={ (x,y): x^2+y^2-4=0}; f(x,y)=xy (povrsina)
Preko teorema o uvjetnim eksretmima dobivam:
kandidate za tocke ekstreme
(sqrt(2),sqrt(2)) i (-sqrt(2),-sqrt(2))
f od ova dva kandidata je je 2.
Da li je ovo ok?[/quote]
2. DA. za dfb ne znam osim da mogu komentirat kak je to komp dfb funkcija. kako bih to dokazala ne znam xD
3 b) ja sam dobila 2,2 i -2,-2 al čini mi se da sam nešto krivo računala al ugl dobro si sve postavila
sada, kako su x,y stranice, ja sam izbacila rješenje -2,-2, odnosno -sqrt2, sqrt2
pa je rj (sqrt2,sqrt2
| frutabella (napisa): | | pedro (napisa): |
-sqrt6 ⇐ x ⇐ sqrt6
-sqrt2 ⇐ y ⇐ sqrt2
0 ⇐ z ⇐ 2
|
Zar ne bi trebalo z ograniciti između -2 i 2?
I moze li malo detaljnije zadatak 2 (znaci sa zavrsenog 2010.)
Hvala
Vidjela sam gore da je rjeseno Df(1,0...0),
domena je valjda Df=R\←besk, 0]; Df'=R
Ovo da je diferencijabilna u svim tockama treba dokazati po definiciji?
Added after 43 minutes:
http://web.math.pmf.unizg.hr/nastava/difraf/dif/2009-10/zavrsni.pdf
3. zad pod b)
Oznacila sam S={ (x,y): x^2+y^2-4=0}; f(x,y)=xy (povrsina)
Preko teorema o uvjetnim eksretmima dobivam:
kandidate za tocke ekstreme
(sqrt(2),sqrt(2)) i (-sqrt(2),-sqrt(2))
f od ova dva kandidata je je 2.
Da li je ovo ok? |
2. DA. za dfb ne znam osim da mogu komentirat kak je to komp dfb funkcija. kako bih to dokazala ne znam xD
3 b) ja sam dobila 2,2 i -2,-2 al čini mi se da sam nešto krivo računala al ugl dobro si sve postavila
sada, kako su x,y stranice, ja sam izbacila rješenje -2,-2, odnosno -sqrt2, sqrt2
pa je rj (sqrt2,sqrt2
|
|
| [Vrh] |
|
frutabella
Forumaš(ica)
Pridružen/a: 09. 10. 2010. (16:35:36)
Postovi: (24E)16
|
|
| [Vrh] |
|
pedro
Forumaš(ica)
Pridružen/a: 21. 10. 2010. (14:08:21)
Postovi: (19B)16
|
|
| [Vrh] |
|
frutabella
Forumaš(ica)
Pridružen/a: 09. 10. 2010. (16:35:36)
Postovi: (24E)16
|
| Postano: 22:07 ned, 20. 1. 2013 Naslov: |
|
|
|
[quote="pedro"][quote="frutabella"]http://web.math.pmf.unizg.hr/nastava/difraf/dif/2009-10/zavrsni.pdf
6. pod a)
Ovo naslucuje na tm 16.2. (nuzni uvjet za lok ekstrem), ali teorem kaze jos da je f dfb u c iz A, sto mi nemamo zadano. Da li je onda odg ne?
I kako sad to dokazati...[/quote]
f je klase C^2, što znači da je dfb u svakoj točki iz A[/quote]
Istina da. :D
Zad 5. pod a)
Da li je ok ovo: f(x,y)=[ 2x^2 2y^2] ?
(btw: da li vi mozete uci na sluzbenu stranicu faksa math.hr, ovo mi je vec drugi dan da mi je stranica nedostupna? )
| pedro (napisa): | | frutabella (napisa): | http://web.math.pmf.unizg.hr/nastava/difraf/dif/2009-10/zavrsni.pdf
6. pod a)
Ovo naslucuje na tm 16.2. (nuzni uvjet za lok ekstrem), ali teorem kaze jos da je f dfb u c iz A, sto mi nemamo zadano. Da li je onda odg ne?
I kako sad to dokazati... |
f je klase C^2, što znači da je dfb u svakoj točki iz A |
Istina da.
Zad 5. pod a)
Da li je ok ovo: f(x,y)=[ 2x^2 2y^2] ?
(btw: da li vi mozete uci na sluzbenu stranicu faksa math.hr, ovo mi je vec drugi dan da mi je stranica nedostupna? )
|
|
| [Vrh] |
|
pedro
Forumaš(ica)
Pridružen/a: 21. 10. 2010. (14:08:21)
Postovi: (19B)16
|
|
| [Vrh] |
|
frutabella
Forumaš(ica)
Pridružen/a: 09. 10. 2010. (16:35:36)
Postovi: (24E)16
|
| Postano: 22:48 ned, 20. 1. 2013 Naslov: |
|
|
|
http://web.math.pmf.unizg.hr/nastava/difraf/dif/2010-11/zavrsni.pdf
1. zad:
jel ok ograniciti (x,y,z) € [0, sqrt(ln4)] ?
A sta cu s ovim pitanjem, da li je otvoren? Pa naravno da nije, ili se ja varam (ne bi valjda to pitanje dzaba tu stojalo :D )
Ili cak je: f(x,y,z) je uvijek > 0, pa moze biti f^-1 ( <0, +besk> ) sto je otvoren.
http://web.math.pmf.unizg.hr/nastava/difraf/dif/2010-11/zavrsni.pdf
1. zad:
jel ok ograniciti (x,y,z) € [0, sqrt(ln4)] ?
A sta cu s ovim pitanjem, da li je otvoren? Pa naravno da nije, ili se ja varam (ne bi valjda to pitanje dzaba tu stojalo )
Ili cak je: f(x,y,z) je uvijek > 0, pa moze biti f^-1 ( <0, +besk> ) sto je otvoren.
|
|
| [Vrh] |
|
pedro
Forumaš(ica)
Pridružen/a: 21. 10. 2010. (14:08:21)
Postovi: (19B)16
|
| Postano: 22:57 ned, 20. 1. 2013 Naslov: |
|
|
|
[quote="frutabella"]http://web.math.pmf.unizg.hr/nastava/difraf/dif/2010-11/zavrsni.pdf
1. zad:
jel ok ograniciti (x,y,z) € [0, sqrt(ln4)] ?
A sta cu s ovim pitanjem, da li je otvoren? Pa naravno da nije, ili se ja varam (ne bi valjda to pitanje dzaba tu stojalo :D )
Ili cak je: f(x,y,z) je uvijek > 0, pa moze biti f^-1 ( <0, +besk> ) sto je otvoren.[/quote]
to sam gore negdje ograničila pa pogledaj :)
a što se tiče otvorenosti, dokazali smo da je kompaktan, što znači da je zatvoren, da bi skup bio otvoren ja bih rekla da moramo dokazati da definira cijeli R^2 jer je taj skup i otvoren i zatvoren, ne znam postoje li manji skupovi koji su ujedino i otvoreni i zatvoreni osim praznog skupa i R^n
dalje, taj skup nije otvoren je vidiš da najmanju vrijednost koju poprimi je -1, pa dalje u - beskonačno nije ni definiran,
ali to je samo moje razmišljanje, i već čekam da me tu netko ispravi al kad niko trenutno nije aktivan :)
tak da nemoj ovo uzeti kao točno rješenje
| frutabella (napisa): | http://web.math.pmf.unizg.hr/nastava/difraf/dif/2010-11/zavrsni.pdf
1. zad:
jel ok ograniciti (x,y,z) € [0, sqrt(ln4)] ?
A sta cu s ovim pitanjem, da li je otvoren? Pa naravno da nije, ili se ja varam (ne bi valjda to pitanje dzaba tu stojalo )
Ili cak je: f(x,y,z) je uvijek > 0, pa moze biti f^-1 ( <0, +besk> ) sto je otvoren. |
to sam gore negdje ograničila pa pogledaj
a što se tiče otvorenosti, dokazali smo da je kompaktan, što znači da je zatvoren, da bi skup bio otvoren ja bih rekla da moramo dokazati da definira cijeli R^2 jer je taj skup i otvoren i zatvoren, ne znam postoje li manji skupovi koji su ujedino i otvoreni i zatvoreni osim praznog skupa i R^n
dalje, taj skup nije otvoren je vidiš da najmanju vrijednost koju poprimi je -1, pa dalje u - beskonačno nije ni definiran,
ali to je samo moje razmišljanje, i već čekam da me tu netko ispravi al kad niko trenutno nije aktivan
tak da nemoj ovo uzeti kao točno rješenje
|
|
| [Vrh] |
|
frutabella
Forumaš(ica)
Pridružen/a: 09. 10. 2010. (16:35:36)
Postovi: (24E)16
|
| Postano: 23:20 ned, 20. 1. 2013 Naslov: |
|
|
|
Kako si 2. rijesila:
Ja sam parcijalno po x i y izracunala ovaj prvi dio (hajmo ga nazvati f1),
isto tako sam i f2. Zakljucim da su neprekidnu na domeni zbog onog standardnog razloga.
Provjerim jos neprekidnost u (x,0) i dobijem da je parcijalno po x-u u toj tocki limes jednak 1,
a po y u toj tocki je 0.
Moram jos dokazati naprekidnost, odnosno
lim ((x,y)--->(x,0)) parcijalno od x od f2 i dobijem da je limes = 1, kao sto i treba.
No, isti taj limes od parijalno po y od f2 mi ne ispada bas 0, znaci ovako:
lim ((x,y)--->(x,0)) -x = -x
Onda nije klase C1
Samo mi se cini da ovdje nesto ne stima, pa bih te zamolila da provjeris.
Kako si 2. rijesila:
Ja sam parcijalno po x i y izracunala ovaj prvi dio (hajmo ga nazvati f1),
isto tako sam i f2. Zakljucim da su neprekidnu na domeni zbog onog standardnog razloga.
Provjerim jos neprekidnost u (x,0) i dobijem da je parcijalno po x-u u toj tocki limes jednak 1,
a po y u toj tocki je 0.
Moram jos dokazati naprekidnost, odnosno
lim ((x,y)--->(x,0)) parcijalno od x od f2 i dobijem da je limes = 1, kao sto i treba.
No, isti taj limes od parijalno po y od f2 mi ne ispada bas 0, znaci ovako:
lim ((x,y)--->(x,0)) -x = -x
Onda nije klase C1
Samo mi se cini da ovdje nesto ne stima, pa bih te zamolila da provjeris.
|
|
| [Vrh] |
|
pedro
Forumaš(ica)
Pridružen/a: 21. 10. 2010. (14:08:21)
Postovi: (19B)16
|
|
| [Vrh] |
|
pedro
Forumaš(ica)
Pridružen/a: 21. 10. 2010. (14:08:21)
Postovi: (19B)16
|
| Postano: 8:12 pon, 21. 1. 2013 Naslov: |
|
|
|
[quote="pedro"]ovo sam rješila sad i poslala feniksu u pp, ako mi je točan postupak copy pastam ti. jer meni je ispala da fun je C1[/quote]
ovako sam išla, prvo parcijalne po x:
fx(x,y) = cos(xy) za y >0
fx(x,y)=1-y za y<=0
fx(x0,0)= lim f(x0+t) -f(x0,0) / t =... = 1
sada provjeravamo je li neprekidno tako da:
lim(x,y)->(x0,0) = fx(x0,0)
opet gledamo zay >0 i y<= 0 posebno i dobijemo
za y>0
lim cos(xy)=cos(0)=1 kada (x,y)->(x0,0)
i za y<=0 dobijemo lim 1-y=1 kada (x,y)->(x0,0)
tu vidimo da se pokapa pa je uredu.
sada za parcijalne po y:
fy(x,y)=[cos(xy)*xy-sin(xy)] /y^2
za y>0
i za y <=0
fy(x,y)=-x
fy(x0,0)=lim f(x0,t)-f(x0,0) / t=...=0 za y>0
za y<=0
fy(x0,0)=...=-x0
opet pokazujemo jesu li jednake, ako jesu neprekidne su i fun je klase C1
posebno za y>0 i posebno za y<=0
i tu neš nemrem dobiti za lim(x,y)->(x0,0) [cos(xy)*xy-sin(xy)] /y^2=... šteka mi ovaj limes Smile; ugl trebalo bi ispast da on teži u 0
onda kako ne znam ubacim u wolfram i dobijem da težni k nul
a za
lim(x,y)->(x0,0) -x=-x0 što je dobro Smile
znači postoje par der i neprekidne su -> funk je klase C1
| pedro (napisa): | | ovo sam rješila sad i poslala feniksu u pp, ako mi je točan postupak copy pastam ti. jer meni je ispala da fun je C1 |
ovako sam išla, prvo parcijalne po x:
fx(x,y) = cos(xy) za y >0
fx(x,y)=1-y za y⇐0
fx(x0,0)= lim f(x0+t) -f(x0,0) / t =... = 1
sada provjeravamo je li neprekidno tako da:
lim(x,y)→(x0,0) = fx(x0,0)
opet gledamo zay >0 i y⇐ 0 posebno i dobijemo
za y>0
lim cos(xy)=cos(0)=1 kada (x,y)→(x0,0)
i za y⇐0 dobijemo lim 1-y=1 kada (x,y)→(x0,0)
tu vidimo da se pokapa pa je uredu.
sada za parcijalne po y:
fy(x,y)=[cos(xy)*xy-sin(xy)] /y^2
za y>0
i za y ⇐0
fy(x,y)=-x
fy(x0,0)=lim f(x0,t)-f(x0,0) / t=...=0 za y>0
za y⇐0
fy(x0,0)=...=-x0
opet pokazujemo jesu li jednake, ako jesu neprekidne su i fun je klase C1
posebno za y>0 i posebno za y⇐0
i tu neš nemrem dobiti za lim(x,y)→(x0,0) [cos(xy)*xy-sin(xy)] /y^2=... šteka mi ovaj limes Smile; ugl trebalo bi ispast da on teži u 0
onda kako ne znam ubacim u wolfram i dobijem da težni k nul
a za
lim(x,y)→(x0,0) -x=-x0 što je dobro Smile
znači postoje par der i neprekidne su → funk je klase C1
|
|
| [Vrh] |
|
|
