| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
Vincent Van Ear
Forumaš(ica)


Pridružen/a: 19. 08. 2004. (11:29:05)
Postovi: (175)16
|
 Postano: 9:48 uto, 24. 8. 2004 Naslov: Prop.-suma koja aproksimira integral Postano: 9:48 uto, 24. 8. 2004 Naslov: Prop.-suma koja aproksimira integral |
    |
|
|
[color=green]Propozicija :
Pretpostavke : f:[a,b]->IR (R)-integrabilna
Doprinos propozicije :
Postoji niz subdivizija {d_n} takav da za svaki izbor točaka oblika { n^t_k } pri čemu je n^t_k@[n^x_k- n^x_k-1] vrijedi :
$f(x)dx=lim_{n->oo} suma po x_k iz d_n pribrojnika oblika :f(n^t_k)*( n^x_k- n^x_k-1)
Nadalje to vrijedi i za svaki niz finijih subdivizija.[/color]
[color=violet]Napomena:
Integral označavam sa $ [/color]
Imam već pitanje iz samih tvrdnji teorema:
definirali smo da je niz funkcija sa IN u IR.
Ali subdivizija nije konkretan realan broj već _skup_ realnih brojeva( d_n={n^x_k} imati n-tu subdiviziju je isto što i imati k točaka te subdivizije)
pa kako onda kažemo da 'imamo niz subdivizija' ?
Dokaz:
Funkcija je (R)-integrabilna => kriterij integrabilnosti
=> postoji određeni integral $f(x)dx u području od a do b
An@IN postoji subdivizija d_n takva da vrijedi S(d_n)-s(d_n)<1/n
d_n={n^x_k} imati n-tu subdiviziju je isto što i imati k točaka te subdivizije
Budući da je s(d_n)<=$f(x)dx<=S(d_n)
Funkcija je po pretpostavci teorema (R)-integrabilna što će reći da donje sume konvergiraju ka integralu odozdo,a gornje odozgo,jezikom limesa :
lim_{n->oo}s(d_n)=$f(x)dx=lim_{n->oo}S(d_n)
uzmimo točke {n^t_k} tako da je n^t_k@[n^x_k-1 , n^x_k] ,tada sigurno vrijedi :
n^m_k<= f(n^t_k) <= n^M_k
ovaj odnos je trivijalan za zaključiti:naša funkcija je (R)-integrabilna pa je nužno i omeđena(jer smo (R)-integrabilnost definirali samo za omeđene funkcije na segmentu) što znači da u svakom podsegmentu svoje domene(segmenta) postiže supremum i infimum.
Točka t iz n-te subdivizije k-tog segmenta odabrana je proizvoljno i ona može i ne mora postići supremum(maksimum) odnosno infimum(minimum).
Pomnožimo gornju nejednakost sa (n^x_k - n^x_k-1) koji je strogo pozitivan pa neće uzrokovati promjenu smjera nejednakosti nejednadžbe.
Dobivamo:
s(d_n)<=suma po n^x_k pribrojnika f(n^t_k)* (n^x_k - n^x_k-1) <=S(d_n)
nizovi s(d_n) i S(d_n) (primjetno je da imamo te nizove jer _svakom_ prirodnom broju pridružujemo njegovu sumu-broj) su konvergenti što je jasno zbog pretpostavke da imamo (R)-integrabilnu funkciju,a između njih je ''zatočena'' suma odnosno neki broj.
Pozivanjem na teorem o sendviču imamo sljedeći doprinos:
lim_{n->oo} suma po n^x_k pribrojnika f(n^t_k)* (n^x_k - n^x_k-1) =$f(x)dx u području od a do b
Drugi dio propozicije sijedi iz činjenice da je s(d_n)<=s(d'_n) te S(d'_n)<=S(d_n)
Q.E.D
Naravno nakon ovog ispisa na forumu ostaje samo nada da ste uspjeli dekriptirati ovaj kod;)
Slobodno ispravite i najmanju sitnicu koju sam krivo postavio jer cijeli ovaj 'support' teksta koji prati simboliku moja je interpretacija iste.
Propozicija :
Pretpostavke : f:[a,b]→IR (R)-integrabilna
Doprinos propozicije :
Postoji niz subdivizija {d_n} takav da za svaki izbor točaka oblika { n^t_k } pri čemu je n^t_k@[n^x_k- n^x_k-1] vrijedi :
$f(x)dx=lim_{n→oo} suma po x_k iz d_n pribrojnika oblika :f(n^t_k)*( n^x_k- n^x_k-1)
Nadalje to vrijedi i za svaki niz finijih subdivizija.
Napomena:
Integral označavam sa $
Imam već pitanje iz samih tvrdnji teorema:
definirali smo da je niz funkcija sa IN u IR.
Ali subdivizija nije konkretan realan broj već _skup_ realnih brojeva( d_n={n^x_k} imati n-tu subdiviziju je isto što i imati k točaka te subdivizije)
pa kako onda kažemo da 'imamo niz subdivizija' ?
Dokaz:
Funkcija je (R)-integrabilna ⇒ kriterij integrabilnosti
⇒ postoji određeni integral $f(x)dx u području od a do b
An@IN postoji subdivizija d_n takva da vrijedi S(d_n)-s(d_n)<1/n
d_n={n^x_k} imati n-tu subdiviziju je isto što i imati k točaka te subdivizije
Budući da je s(d_n)⇐$f(x)dx⇐S(d_n)
Funkcija je po pretpostavci teorema (R)-integrabilna što će reći da donje sume konvergiraju ka integralu odozdo,a gornje odozgo,jezikom limesa :
lim_{n→oo}s(d_n)=$f(x)dx=lim_{n→oo}S(d_n)
uzmimo točke {n^t_k} tako da je n^t_k@[n^x_k-1 , n^x_k] ,tada sigurno vrijedi :
n^m_k⇐ f(n^t_k) ⇐ n^M_k
ovaj odnos je trivijalan za zaključiti:naša funkcija je (R)-integrabilna pa je nužno i omeđena(jer smo (R)-integrabilnost definirali samo za omeđene funkcije na segmentu) što znači da u svakom podsegmentu svoje domene(segmenta) postiže supremum i infimum.
Točka t iz n-te subdivizije k-tog segmenta odabrana je proizvoljno i ona može i ne mora postići supremum(maksimum) odnosno infimum(minimum).
Pomnožimo gornju nejednakost sa (n^x_k - n^x_k-1) koji je strogo pozitivan pa neće uzrokovati promjenu smjera nejednakosti nejednadžbe.
Dobivamo:
s(d_n)⇐suma po n^x_k pribrojnika f(n^t_k)* (n^x_k - n^x_k-1) ⇐S(d_n)
nizovi s(d_n) i S(d_n) (primjetno je da imamo te nizove jer _svakom_ prirodnom broju pridružujemo njegovu sumu-broj) su konvergenti što je jasno zbog pretpostavke da imamo (R)-integrabilnu funkciju,a između njih je ''zatočena'' suma odnosno neki broj.
Pozivanjem na teorem o sendviču imamo sljedeći doprinos:
lim_{n→oo} suma po n^x_k pribrojnika f(n^t_k)* (n^x_k - n^x_k-1) =$f(x)dx u području od a do b
Drugi dio propozicije sijedi iz činjenice da je s(d_n)⇐s(d'_n) te S(d'_n)⇐S(d_n)
Q.E.D
Naravno nakon ovog ispisa na forumu ostaje samo nada da ste uspjeli dekriptirati ovaj kod;)
Slobodno ispravite i najmanju sitnicu koju sam krivo postavio jer cijeli ovaj 'support' teksta koji prati simboliku moja je interpretacija iste.
_________________
Samo sam jedan čovjek,
samo jedan pakao.
|
|
| [Vrh] |
|
vsego
Site Admin


Pridružen/a: 06. 10. 2002. (22:07:09)
Postovi: (3562)16
Spol: 
Lokacija: /sbin/init
|
 Postano: 11:07 uto, 24. 8. 2004 Naslov: Re: Prop.-suma koja aproksimira integral Postano: 11:07 uto, 24. 8. 2004 Naslov: Re: Prop.-suma koja aproksimira integral |
    |
|
|
Nisam u moodu za "trcanje" kroz cijeli dokaz, a i kratak sam s vremenom... :|
[quote="Vincent Van Ear"][color=green]Propozicija :
Pretpostavke : f:[a,b]->IR (R)-integrabilna
Doprinos propozicije :
Postoji niz subdivizija {d_n} takav da za svaki izbor točaka oblika { n^t_k } pri čemu je n^t_k@[n^x_k- n^x_k-1] vrijedi :
$f(x)dx=lim_{n->oo} suma po x_k iz d_n pribrojnika oblika :f(n^t_k)*( n^x_k- n^x_k-1)
Nadalje to vrijedi i za svaki niz finijih subdivizija.[/color]
definirali smo da je niz funkcija sa IN u IR.
Ali subdivizija nije konkretan realan broj već _skup_ realnih brojeva( d_n={n^x_k} imati n-tu subdiviziju je isto što i imati k točaka te subdivizije)
pa kako onda kažemo da 'imamo niz subdivizija' ?[/quote]
"[i]definirali smo da je niz funkcija sa IN u IR.[/i]" :arrow: to je niz realnih brojeva. :)
Opcenito, [b]niz je proizvoljna funkcija s |N u bilo koji skup[/b]. 8)
Dakle, niz subdivizija je, u stvari, funkcija iz |N u P([a,b]) (partitivni skup skupa [a,b]). :D Dakle, funkcija koja [b]svakom[/b] prirodnom broju pridruzuje neki podskup od [a,b]. :-s Elementi tog podskupa su granice unutar subdivizije... :)
Nisam u moodu za "trcanje" kroz cijeli dokaz, a i kratak sam s vremenom... 
| Vincent Van Ear (napisa): | Propozicija :
Pretpostavke : f:[a,b]→IR (R)-integrabilna
Doprinos propozicije :
Postoji niz subdivizija {d_n} takav da za svaki izbor točaka oblika { n^t_k } pri čemu je n^t_k@[n^x_k- n^x_k-1] vrijedi :
$f(x)dx=lim_{n→oo} suma po x_k iz d_n pribrojnika oblika :f(n^t_k)*( n^x_k- n^x_k-1)
Nadalje to vrijedi i za svaki niz finijih subdivizija.
definirali smo da je niz funkcija sa IN u IR.
Ali subdivizija nije konkretan realan broj već _skup_ realnih brojeva( d_n={n^x_k} imati n-tu subdiviziju je isto što i imati k točaka te subdivizije)
pa kako onda kažemo da 'imamo niz subdivizija' ? |
"definirali smo da je niz funkcija sa IN u IR."  to je niz realnih brojeva. to je niz realnih brojeva. 
Opcenito, niz je proizvoljna funkcija s |N u bilo koji skup. 
Dakle, niz subdivizija je, u stvari, funkcija iz |N u P([a,b]) (partitivni skup skupa [a,b]).  Dakle, funkcija koja svakom prirodnom broju pridruzuje neki podskup od [a,b]. Dakle, funkcija koja svakom prirodnom broju pridruzuje neki podskup od [a,b].  Elementi tog podskupa su granice unutar subdivizije... Elementi tog podskupa su granice unutar subdivizije... 
_________________ U pravilu ignoriram pitanja u krivim topicima i kodove koji nisu u [code]...[/code] blokovima.
Takodjer, OBJASNITE sto vas muci! "Sto mi je krivo?", bez opisa u cemu je problem, rijetko ce zadobiti moju paznju.  |
|
| [Vrh] |
|
Vincent Van Ear
Forumaš(ica)


Pridružen/a: 19. 08. 2004. (11:29:05)
Postovi: (175)16
|
 Postano: 12:06 uto, 24. 8. 2004 Naslov: Postano: 12:06 uto, 24. 8. 2004 Naslov: |
    |
|
|
[quote]Opcenito, niz je proizvoljna funkcija s |N u bilo koji skup.
Dakle, niz subdivizija je, u stvari, funkcija iz |N u P([a,b]) (partitivni skup skupa [a,b]). Dakle, funkcija koja svakom prirodnom broju pridruzuje neki podskup od [a,b]. Elementi tog podskupa su granice unutar subdivizije... [/quote]
A tako dakle :) onda u redu,hvala ti. :wink:
| Citat: | Opcenito, niz je proizvoljna funkcija s |N u bilo koji skup.
Dakle, niz subdivizija je, u stvari, funkcija iz |N u P([a,b]) (partitivni skup skupa [a,b]). Dakle, funkcija koja svakom prirodnom broju pridruzuje neki podskup od [a,b]. Elementi tog podskupa su granice unutar subdivizije... |
A tako dakle  onda u redu,hvala ti. onda u redu,hvala ti. 
_________________
Samo sam jedan čovjek,
samo jedan pakao.
|
|
| [Vrh] |
|
Vincent Van Ear
Forumaš(ica)


Pridružen/a: 19. 08. 2004. (11:29:05)
Postovi: (175)16
|
|
| [Vrh] |
|
ZELENIZUBNAPLANETIDO
SADE
Forumaš(ica)


Pridružen/a: 04. 03. 2004. (19:56:15)
Postovi: (54F)16
Lokacija: hm?
|
 Postano: 12:37 sri, 25. 8. 2004 Naslov: Postano: 12:37 sri, 25. 8. 2004 Naslov: |
    |
|
|
[quote="Vincent Van Ear"]Hajde da riječima prokomentiram što tvrdnja teorema govori:
Ako je funkcija (R)-integrabilna onda će postojati niz subdivizija(njih prebrojivo mnogo) takvih da će biti apsolutno svejedno koje točke iz subdivizija svakog pojedinog podsegmenta odaberem vrijedit će da će limes takvih suma iću u Reimanov integral.
Što znači ovo-za svaki izbor točaka?[/quote]
Tocno to :) Ako sam dobro shvatio, imamo neki niz subdivizija koji ce nas za n->oo voditi do kriterija (R)-integrabilnosti, tj. do gornjeg ili donjeg (R) integrala (koji su u isti, rimembr) i teorem kaze da cu dobiti istu tu relaciju ako odaberem bilo koju tocku iz podsegmenta subdivizije (tj. da ne moram nuzno traziti najvecu i najmanju vrijednost za raspis sume), a to bi cak i intuitivno trebalo biti potpuno jasno: ako je limes svih najvecih fjskih vrijednosti jednak limesu svih najmanjih fjskih vrijednosti, tada via sendvica zakljucujem da to vrijedi i za sve medjuvrijednosti (via BW. tm)
[quote="Vincent Van Ear"]Pa podsegmenti su toliko mali da je razlika točaka unutar segmenta mizerna odnosno podsegmenti su birani tako da svaka točka podsegmenta ima okolinu točaka koje ju u potpunosti određuju.
Imam li pravo?[/quote]
Nije _MIZERNA_ :D, nije cak ni poanta dokaza da je "jaaako mala", poanta je u tome da svaki drugi izbor tocaka koje ces uvaliti u svoju pseudodarboux sumu kada ih uvalimo u limes dati tvoju brojcanu vrijednost integrala. :) Sendvic ! :) :klopa:
[quote="Vincent Van Ear"]Subdivizija sa svojstvom iz teorema ima zapravo neprebrojivo mnogo(njih inače ima neprebrojivo mnogo je je subdivizija konačan skup točaka iz segmenata,a točaka za odabir ima neprebrojivo mnogo pa nikada ne iscrpljujem broj mogućnosti) ali nama je dovoljno imati njih prebrojivo mnogo,između ostaloga zbog mogućnosti korištenja terminologije nizova u samom teoremu.
Imam li pravo?[/quote]
Subdivizija sa takvim svojstvom, ima jako mnogo, slutim i neprebrojivo mnogo iako to nismo dokazali, a i nije ni toliko bitno (buduci da mozes imati i prebrojivo mnogo tocaka pa da nikada ne iscpris mogucnosti odabira prebrojivog broja tocaka ;), vidi primjer na kraju). Iako da, u pravu si, uz dobar odabir nam je i prebrojivo mnogo subdivizija dovoljno :)
[latex]\bigcup_{p\_prost}\{k*p \in N : k \in N\} \subset N[/latex] jest primjer unije prebrojivog broja prebrojivih skupova koja je _pravi_ podskup prebrojivog skupa :g:
| Vincent Van Ear (napisa): | Hajde da riječima prokomentiram što tvrdnja teorema govori:
Ako je funkcija (R)-integrabilna onda će postojati niz subdivizija(njih prebrojivo mnogo) takvih da će biti apsolutno svejedno koje točke iz subdivizija svakog pojedinog podsegmenta odaberem vrijedit će da će limes takvih suma iću u Reimanov integral.
Što znači ovo-za svaki izbor točaka? |
Tocno to  Ako sam dobro shvatio, imamo neki niz subdivizija koji ce nas za n→oo voditi do kriterija (R)-integrabilnosti, tj. do gornjeg ili donjeg (R) integrala (koji su u isti, rimembr) i teorem kaze da cu dobiti istu tu relaciju ako odaberem bilo koju tocku iz podsegmenta subdivizije (tj. da ne moram nuzno traziti najvecu i najmanju vrijednost za raspis sume), a to bi cak i intuitivno trebalo biti potpuno jasno: ako je limes svih najvecih fjskih vrijednosti jednak limesu svih najmanjih fjskih vrijednosti, tada via sendvica zakljucujem da to vrijedi i za sve medjuvrijednosti (via BW. tm) Ako sam dobro shvatio, imamo neki niz subdivizija koji ce nas za n→oo voditi do kriterija (R)-integrabilnosti, tj. do gornjeg ili donjeg (R) integrala (koji su u isti, rimembr) i teorem kaze da cu dobiti istu tu relaciju ako odaberem bilo koju tocku iz podsegmenta subdivizije (tj. da ne moram nuzno traziti najvecu i najmanju vrijednost za raspis sume), a to bi cak i intuitivno trebalo biti potpuno jasno: ako je limes svih najvecih fjskih vrijednosti jednak limesu svih najmanjih fjskih vrijednosti, tada via sendvica zakljucujem da to vrijedi i za sve medjuvrijednosti (via BW. tm)
| Vincent Van Ear (napisa): | Pa podsegmenti su toliko mali da je razlika točaka unutar segmenta mizerna odnosno podsegmenti su birani tako da svaka točka podsegmenta ima okolinu točaka koje ju u potpunosti određuju.
Imam li pravo? |
Nije _MIZERNA_  , nije cak ni poanta dokaza da je "jaaako mala", poanta je u tome da svaki drugi izbor tocaka koje ces uvaliti u svoju pseudodarboux sumu kada ih uvalimo u limes dati tvoju brojcanu vrijednost integrala. , nije cak ni poanta dokaza da je "jaaako mala", poanta je u tome da svaki drugi izbor tocaka koje ces uvaliti u svoju pseudodarboux sumu kada ih uvalimo u limes dati tvoju brojcanu vrijednost integrala.  Sendvic ! Sendvic !  
| Vincent Van Ear (napisa): | Subdivizija sa svojstvom iz teorema ima zapravo neprebrojivo mnogo(njih inače ima neprebrojivo mnogo je je subdivizija konačan skup točaka iz segmenata,a točaka za odabir ima neprebrojivo mnogo pa nikada ne iscrpljujem broj mogućnosti) ali nama je dovoljno imati njih prebrojivo mnogo,između ostaloga zbog mogućnosti korištenja terminologije nizova u samom teoremu.
Imam li pravo? |
Subdivizija sa takvim svojstvom, ima jako mnogo, slutim i neprebrojivo mnogo iako to nismo dokazali, a i nije ni toliko bitno (buduci da mozes imati i prebrojivo mnogo tocaka pa da nikada ne iscpris mogucnosti odabira prebrojivog broja tocaka  , vidi primjer na kraju). Iako da, u pravu si, uz dobar odabir nam je i prebrojivo mnogo subdivizija dovoljno , vidi primjer na kraju). Iako da, u pravu si, uz dobar odabir nam je i prebrojivo mnogo subdivizija dovoljno 
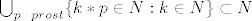 jest primjer unije prebrojivog broja prebrojivih skupova koja je _pravi_ podskup prebrojivog skupa jest primjer unije prebrojivog broja prebrojivih skupova koja je _pravi_ podskup prebrojivog skupa 
_________________ 
Pupoljak nije negiran. Rekao sam to i ponovit cu to jos jedanput. Pupoljak NIJE negirAn.
MADD
(Mothers Against Dirty Dialectics)
Based on a true story. NOT.
Ko ih sljivi, mi sviramo punk  |
|
| [Vrh] |
|
Vincent Van Ear
Forumaš(ica)


Pridružen/a: 19. 08. 2004. (11:29:05)
Postovi: (175)16
|
|
| [Vrh] |
|
ZELENIZUBNAPLANETIDO
SADE
Forumaš(ica)


Pridružen/a: 04. 03. 2004. (19:56:15)
Postovi: (54F)16
Lokacija: hm?
|
 Postano: 14:23 sri, 25. 8. 2004 Naslov: Postano: 14:23 sri, 25. 8. 2004 Naslov: |
    |
|
|
[quote="Vincent Van Ear"] [quote]jest primjer unije prebrojivog broja prebrojivih skupova koja je _pravi_ podskup prebrojivog skupa [/quote]
Zbog tvog primjera imam vrećicu leda na glavi :boliglava: ,pa ti eto hvala.
Again,thnx.
:wink:[/quote]
I drugi put :g:
| Vincent Van Ear (napisa): | | Citat: | | jest primjer unije prebrojivog broja prebrojivih skupova koja je _pravi_ podskup prebrojivog skupa |
Zbog tvog primjera imam vrećicu leda na glavi  ,pa ti eto hvala. ,pa ti eto hvala.
Again,thnx.
 |
I drugi put 
_________________ 
Pupoljak nije negiran. Rekao sam to i ponovit cu to jos jedanput. Pupoljak NIJE negirAn.
MADD
(Mothers Against Dirty Dialectics)
Based on a true story. NOT.
Ko ih sljivi, mi sviramo punk  |
|
| [Vrh] |
|
Vincent Van Ear
Forumaš(ica)


Pridružen/a: 19. 08. 2004. (11:29:05)
Postovi: (175)16
|
|
| [Vrh] |
|
|





