| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
Gost
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
Gost
|
 Postano: 23:37 ned, 15. 8. 2004 Naslov: Postano: 23:37 ned, 15. 8. 2004 Naslov: |
    |
|
|
uh,neznam što mi je danas! :shock:
Kolega,opet ja ne vidim što Vi vidite,finalno:
(-1)^n+1 * [1*3*...*(2*n-3)]/[ 2^n*x^[color=red]n[/color]-1/2 ] 8)
Smijem li onda na ispitu napisati da mi ta formula vrijedi za n>1,a za n=1 imam y'=1/2*x^-1/2 ?
Meni se to čini sasvim korektno,time sam obuhvatio svaku derivaciju višeg reda koja se od mene zahtjeva,jeli ?
uh,neznam što mi je danas! 
Kolega,opet ja ne vidim što Vi vidite,finalno:
(-1)^n+1 * [1*3*...*(2*n-3)]/[ 2^n*x^n-1/2 ] 
Smijem li onda na ispitu napisati da mi ta formula vrijedi za n>1,a za n=1 imam y'=1/2*x^-1/2 ?
Meni se to čini sasvim korektno,time sam obuhvatio svaku derivaciju višeg reda koja se od mene zahtjeva,jeli ?
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
vsego
Site Admin


Pridružen/a: 06. 10. 2002. (22:07:09)
Postovi: (3562)16
Spol: 
Lokacija: /sbin/init
|
 Postano: 2:39 pon, 16. 8. 2004 Naslov: Postano: 2:39 pon, 16. 8. 2004 Naslov: |
    |
|
|
[quote="Anonymous"]Da, to je OK. A, usput, mislim da se ne bi ni s puno bodova kaznio previd da onaj opći izraz ne stoji za n=1.[/quote]
Zasto ne stoji? :-k
[latex](-1)^{n+1} \frac{1\cdot3\cdot\ldots\cdot(2n-3)}{2^n \cdot x^{n-1/2}}[/latex]
Drugim rijecima:
[latex](-1)^{n+1} \frac{\prod_{k=2}^{k\leq n}2k-3}{2^n \cdot x^{n-1/2}}[/latex]
Ili, trivijalnom supstitucijom:
[latex](-1)^{n+1} \frac{\prod_{k=1}^{k<n}2k-1}{2^n \cdot x^{n-1/2}}[/latex]
Za n=1 imamo prazan produkt: [latex]\prod_{k=1}^{k<1}2k-1=1[/latex]. Kad se to uvrsti, imamo:
[latex](-1)^{1+1} \frac{\prod_{k=1}^{k<1}2k-1}{2^1 \cdot x^{1-1/2}} = \frac{1}{2 \cdot x^{1/2}} = \frac{1}{2\sqrt{x}}[/latex]
To je ok, zar ne? ;)
Zasto je onaj produkt bas 1? :-k Zato jer je 1 neutralni element za mnozenje. :-s Slicno kao: [i]Kolika je suma od nula brojeva?[/i] :? Jasno, nula - neutralni element za zbrajanje. 8)
| Anonymous (napisa): | | Da, to je OK. A, usput, mislim da se ne bi ni s puno bodova kaznio previd da onaj opći izraz ne stoji za n=1. |
Zasto ne stoji? 
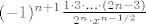
Drugim rijecima:
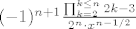
Ili, trivijalnom supstitucijom:
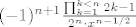
Za n=1 imamo prazan produkt: 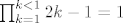 . Kad se to uvrsti, imamo: . Kad se to uvrsti, imamo:
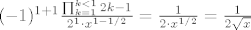
To je ok, zar ne? 
Zasto je onaj produkt bas 1?  Zato jer je 1 neutralni element za mnozenje. Zato jer je 1 neutralni element za mnozenje.  Slicno kao: Kolika je suma od nula brojeva? Slicno kao: Kolika je suma od nula brojeva?  Jasno, nula - neutralni element za zbrajanje. Jasno, nula - neutralni element za zbrajanje. 
_________________ U pravilu ignoriram pitanja u krivim topicima i kodove koji nisu u [code]...[/code] blokovima.
Takodjer, OBJASNITE sto vas muci! "Sto mi je krivo?", bez opisa u cemu je problem, rijetko ce zadobiti moju paznju.  |
|
| [Vrh] |
|
ZELENIZUBNAPLANETIDO
SADE
Forumaš(ica)


Pridružen/a: 04. 03. 2004. (19:56:15)
Postovi: (54F)16
Lokacija: hm?
|
|
| [Vrh] |
|
Gost
|
|
| [Vrh] |
|
vsego
Site Admin


Pridružen/a: 06. 10. 2002. (22:07:09)
Postovi: (3562)16
Spol: 
Lokacija: /sbin/init
|
 Postano: 14:24 pon, 16. 8. 2004 Naslov: Postano: 14:24 pon, 16. 8. 2004 Naslov: |
    |
|
|
[quote="ZELENIZUBNAPLANETIDOSADE"][quote="vsego"]Zasto je onaj produkt bas 1? :-k Zato jer je 1 neutralni element za mnozenje. :-s Slicno kao: [i]Kolika je suma od nula brojeva?[/i] :? Jasno, nula - neutralni element za zbrajanje. 8)[/quote]
:-s Bzz Nikad cuo za to :-s Prazan produkt je tako definiran ili.. ?[/quote]
znam da se tako uzima. :) Da li je definicija ili ne - ne znam. :| Evo ti par argumentacija:[list=1][*]Imas niz [latex](a_k)_k, a_k \neq 0[/latex]. Umnozak prvih [i]n[/i] brojeva je [latex]P_n = \prod_{k=1}^{k \leq n}k[/latex]. Umnozak prvih [i]n+1[/i] je [latex]P_{n+1} = \prod_{k=1}^{k \leq n+1}k = P_n\cdot a_{n+1}[/latex]. Sada uvrsti [i]n[/i]=0. 8)
[*]Imas nula brojeva i pripadni produkt [latex]P_0[/latex]. S druge strane, nula brojeva je isto sto i dva puta nula brojeva, pa je pripadni produkt [latex]P_0^2[/latex].
Ok, uz ovakvu argumentaciju, moglo bi biti i 0, ali ako uzmes u obzir argumentaciju iz tocke 1... 8)[/list:o][quote="ZELENIZUBNAPLANETIDOSADE"][latex]\prod_{k=1}^{k<1}(2k-1) = 1[/latex] :)[/quote]
Ako pitas za zagrade, da, trebaju, ali cesto se preskacu kad se zna o cemu je rijec. :-s
| ZELENIZUBNAPLANETIDOSADE (napisa): | | vsego (napisa): | Zasto je onaj produkt bas 1?  Zato jer je 1 neutralni element za mnozenje. Zato jer je 1 neutralni element za mnozenje.  Slicno kao: Kolika je suma od nula brojeva? Slicno kao: Kolika je suma od nula brojeva?  Jasno, nula - neutralni element za zbrajanje. Jasno, nula - neutralni element za zbrajanje.  |
 Bzz Nikad cuo za to Bzz Nikad cuo za to  Prazan produkt je tako definiran ili.. ? Prazan produkt je tako definiran ili.. ? |
znam da se tako uzima.  Da li je definicija ili ne - ne znam. Da li je definicija ili ne - ne znam.  Evo ti par argumentacija: Evo ti par argumentacija:- Imas niz
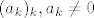 . Umnozak prvih n brojeva je . Umnozak prvih n brojeva je 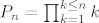 . Umnozak prvih n+1 je . Umnozak prvih n+1 je 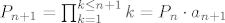 . Sada uvrsti n=0. . Sada uvrsti n=0. 
- Imas nula brojeva i pripadni produkt
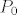 . S druge strane, nula brojeva je isto sto i dva puta nula brojeva, pa je pripadni produkt . S druge strane, nula brojeva je isto sto i dva puta nula brojeva, pa je pripadni produkt 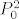 . .
Ok, uz ovakvu argumentaciju, moglo bi biti i 0, ali ako uzmes u obzir argumentaciju iz tocke 1... 
| ZELENIZUBNAPLANETIDOSADE (napisa): | 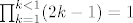  |
Ako pitas za zagrade, da, trebaju, ali cesto se preskacu kad se zna o cemu je rijec. 
_________________ U pravilu ignoriram pitanja u krivim topicima i kodove koji nisu u [code]...[/code] blokovima.
Takodjer, OBJASNITE sto vas muci! "Sto mi je krivo?", bez opisa u cemu je problem, rijetko ce zadobiti moju paznju.  |
|
| [Vrh] |
|
veky
Forumaš(ica)

Pridružen/a: 09. 12. 2002. (19:59:43)
Postovi: (5B0)16
Lokacija: negdje daleko...
|
 Postano: 11:23 pet, 27. 8. 2004 Naslov: Postano: 11:23 pet, 27. 8. 2004 Naslov: |
    |
|
|
[quote="Anonymous"]Iskreno rečeno, radije napišem posebno slučaj n=1 nego da se upuštam u prazan produkt, ali tko voli...[/quote]
Jedan od velikih uvida u mathu je i da _nema specijalnih slučajeva_. Odnosno, to je bar ideal kojem treba težiti. Ljepota neke teorije često se, ne samo u mathu, prilično direktno odnosi s njenom općenitošću, odnosno manjkom specijalnih slučajeva i čudnih grananja s još čudnijim kriterijima.
ZF, trenutni temelj matha, i na njemu bazirana aritmetika prirodnih brojeva, tu čine jako dobar posao. Da, 0^0 = 0! = 1 , kao i svi ostali prazni produkti - i to nije nikakav "posebni dogovor", već jednostavna posljedica prirodnih definicijâ produkta, potenciranja i faktorijele u ZF. Konkretno za potenciranje se blagi uvod može pročitati na http://web.math.hr/~veky/hsmath/L1/ztzio.html .
HTH,
| Anonymous (napisa): | | Iskreno rečeno, radije napišem posebno slučaj n=1 nego da se upuštam u prazan produkt, ali tko voli... |
Jedan od velikih uvida u mathu je i da _nema specijalnih slučajeva_. Odnosno, to je bar ideal kojem treba težiti. Ljepota neke teorije često se, ne samo u mathu, prilično direktno odnosi s njenom općenitošću, odnosno manjkom specijalnih slučajeva i čudnih grananja s još čudnijim kriterijima.
ZF, trenutni temelj matha, i na njemu bazirana aritmetika prirodnih brojeva, tu čine jako dobar posao. Da, 0^0 = 0! = 1 , kao i svi ostali prazni produkti - i to nije nikakav "posebni dogovor", već jednostavna posljedica prirodnih definicijâ produkta, potenciranja i faktorijele u ZF. Konkretno za potenciranje se blagi uvod može pročitati na http://web.math.hr/~veky/hsmath/L1/ztzio.html .
HTH,
|
|
| [Vrh] |
|
|






