| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
Gost
|
 Postano: 18:13 čet, 26. 8. 2004 Naslov: Neprekidne i prekidne funkcije |
    |
|
|
Dali postoji funkcija da je neprekidna na svojoj domeni,a u pravilu pridruživanja posjeduje prekidnu funkciju,dakle da u pravilu imamo buškuriš funkcija,recimo sve redom neprekidne osim jedne ?
Ima li neki teorem u svezi toga ?
Kontekst u kojem mi treba takva informacija:
Recimo funkcija [x]-(x-[x]) je prekidna,u pravilu pridruživanja posjeduje neprekidnu i prekidnu funkciju.Vidim da u izrazu ima prekidnu funkciju,sad,smijem li odmah zaključiti da je neprekidna?
I sad,da bih uspješno došao do površine te funkcije u području domene od točke 2 do 4 moram rasparcelirati tu funkciju na područja na kojima je ona _neprekidna_ kako bih smio primijeniti formulu za integriranje 'F(4)-F(2)=integral od f' jer teorem koji dozvoljava uporabu te krucijalne formule zahtjeva funkciju f na segmentu i neprekidnu.
Dali postoji funkcija da je neprekidna na svojoj domeni,a u pravilu pridruživanja posjeduje prekidnu funkciju,dakle da u pravilu imamo buškuriš funkcija,recimo sve redom neprekidne osim jedne ?
Ima li neki teorem u svezi toga ?
Kontekst u kojem mi treba takva informacija:
Recimo funkcija [x]-(x-[x]) je prekidna,u pravilu pridruživanja posjeduje neprekidnu i prekidnu funkciju.Vidim da u izrazu ima prekidnu funkciju,sad,smijem li odmah zaključiti da je neprekidna?
I sad,da bih uspješno došao do površine te funkcije u području domene od točke 2 do 4 moram rasparcelirati tu funkciju na područja na kojima je ona _neprekidna_ kako bih smio primijeniti formulu za integriranje 'F(4)-F(2)=integral od f' jer teorem koji dozvoljava uporabu te krucijalne formule zahtjeva funkciju f na segmentu i neprekidnu.
|
|
| [Vrh] |
|
Vincent Van Ear
Forumaš(ica)
Pridružen/a: 19. 08. 2004. (11:29:05)
Postovi: (175)16
|
| Postano: 18:19 čet, 26. 8. 2004 Naslov: |
|
|
|
Dali postoji funkcija da je neprekidna na svojoj domeni,a u pravilu pridruživanja posjeduje prekidnu funkciju,dakle da u pravilu imamo buškuriš funkcija,recimo sve redom neprekidne osim jedne ?
Ima li neki teorem u svezi toga ?
Kontekst u kojem mi treba takva informacija:
Recimo funkcija [x]-(x-[x]) je prekidna,u pravilu pridruživanja posjeduje neprekidnu i prekidnu funkciju.Vidim da u izrazu ima prekidnu funkciju,sad,smijem li odmah zaključiti da je prekidna?
I sad,da bih uspješno došao do površine te funkcije u području domene od točke 2 do 4 moram rasparcelirati tu funkciju na područja na kojima je ona _neprekidna_ kako bih smio primijeniti formulu za integriranje 'F(4)-F(2)=integral od f' jer teorem koji dozvoljava uporabu te krucijalne formule zahtjeva funkciju f na segmentu i neprekidnu.
PS:prvo-nisam znao da nisam logiran :)
drugo-odmah sam ispravio tipfeler :wink:
Dali postoji funkcija da je neprekidna na svojoj domeni,a u pravilu pridruživanja posjeduje prekidnu funkciju,dakle da u pravilu imamo buškuriš funkcija,recimo sve redom neprekidne osim jedne ?
Ima li neki teorem u svezi toga ?
Kontekst u kojem mi treba takva informacija:
Recimo funkcija [x]-(x-[x]) je prekidna,u pravilu pridruživanja posjeduje neprekidnu i prekidnu funkciju.Vidim da u izrazu ima prekidnu funkciju,sad,smijem li odmah zaključiti da je prekidna?
I sad,da bih uspješno došao do površine te funkcije u području domene od točke 2 do 4 moram rasparcelirati tu funkciju na područja na kojima je ona _neprekidna_ kako bih smio primijeniti formulu za integriranje 'F(4)-F(2)=integral od f' jer teorem koji dozvoljava uporabu te krucijalne formule zahtjeva funkciju f na segmentu i neprekidnu.
PS:prvo-nisam znao da nisam logiran 
drugo-odmah sam ispravio tipfeler 
_________________
Samo sam jedan čovjek,
samo jedan pakao.
|
|
| [Vrh] |
|
mdoko
Forumaš(ica)
Pridružen/a: 30. 11. 2002. (22:17:12)
Postovi: (71A)16
Spol: 
Lokacija: Heriot-Watt University, Edinburgh
|
| Postano: 19:14 čet, 26. 8. 2004 Naslov: |
|
|
|
Jasno da mozes preko funksije koja nije neprekidna definirati funkciju koja je neprekidna, evo primjer koji je prilicno trivijalan, cak bi se moglo reci i degeneriran, ali kao kontraprimjer je valjan. f(x) = g(x) - g(x) je neprekidna bez obzira sto je funkcija g.
Cini se da je tvoj problem sto pravilo pridruzivanja poistovjecujes s 'formulom'. Pravilo pridruzivanja je nedefiniran pojam i koristi se kada zelimo izbjeci definiranje funkcije preko pojma relacije, sto je u svakom slucaju preciznije i smanjuje mogucnost zabune jer nema dodatnih primitivnih pojmova kao sto je 'pravilo pridruzivanja'. Ipak ponekad je dobro (recimo u analizi) na funkciju gledati na takav nacin, jer se ne treba gubiti vrijeme na stvari koje nisu u sredistu promatranja, ali ipak bi trebalo imati na umu sto je to u stvari funkcija da bi se izbjegli ovakvi i slicni problemi.
Sada da se vratim na problem integriranja. Kada integriras neku funkciju koja nije neprekidna, ili joj je tesko naci primitivnu funkciju, a 'po djelovima' je jednostavnija (neprekidna ili ima jednostavniju primitivnu funkciju) onda je razuman nacin integriranja te funkcije da se integrira posebno po tim djelovima (podsegmentima).
Jasno da mozes preko funksije koja nije neprekidna definirati funkciju koja je neprekidna, evo primjer koji je prilicno trivijalan, cak bi se moglo reci i degeneriran, ali kao kontraprimjer je valjan. f(x) = g(x) - g(x) je neprekidna bez obzira sto je funkcija g.
Cini se da je tvoj problem sto pravilo pridruzivanja poistovjecujes s 'formulom'. Pravilo pridruzivanja je nedefiniran pojam i koristi se kada zelimo izbjeci definiranje funkcije preko pojma relacije, sto je u svakom slucaju preciznije i smanjuje mogucnost zabune jer nema dodatnih primitivnih pojmova kao sto je 'pravilo pridruzivanja'. Ipak ponekad je dobro (recimo u analizi) na funkciju gledati na takav nacin, jer se ne treba gubiti vrijeme na stvari koje nisu u sredistu promatranja, ali ipak bi trebalo imati na umu sto je to u stvari funkcija da bi se izbjegli ovakvi i slicni problemi.
Sada da se vratim na problem integriranja. Kada integriras neku funkciju koja nije neprekidna, ili joj je tesko naci primitivnu funkciju, a 'po djelovima' je jednostavnija (neprekidna ili ima jednostavniju primitivnu funkciju) onda je razuman nacin integriranja te funkcije da se integrira posebno po tim djelovima (podsegmentima).
_________________
Extraordinary claims require extraordinary evidence. – Carl Sagan
|
|
| [Vrh] |
|
Vincent Van Ear
Forumaš(ica)
Pridružen/a: 19. 08. 2004. (11:29:05)
Postovi: (175)16
|
| Postano: 20:46 čet, 26. 8. 2004 Naslov: |
|
|
|
Kako bi ti ovu funkciju [x]-(x-[x]) ''imenovao'' prekidnom,a nalaziš se recimo na ispitu gdje naravno nemaš vremena čarobirati sa definicijom neprekidnosti kojom bi dokazao da je ta funkcija neprekidna(ako bi uopće dokazao).
Postoji li efektivan(brz) način da to saznam?
Ovako znam da je funkcija 'najveće cijelo' prekidna i onda onako napamet(štreberski) zaključujem da je i ova gore prekidna,a argumenta i dokaza nemam.
[quote]Cini se da je tvoj problem sto pravilo pridruzivanja poistovjecujes s 'formulom'.[/quote]
Pa tako nam je rečeno.
Recimo domenu funkcije smo na analizi I definirali ovako:
Domena funkcije je skup svih vrijednosti za koje mogu obaviti sve računske operacije koje mi se u _pravilu pridruživanja_ javljaju.
[quote]Kada integriras neku funkciju koja nije neprekidna...[/quote]
Znam li ja integrirati uopće išta što je prekidno osim ako ne rasparceliram funkciju na neprekidne dijelove domene ?
Ja samo znam za fundamentalan teorem,kako smo ga nazvali,koji mi omogućuje da izračunam površine određenih integrala uz potrebne pretpostavke za funkciju od kojih je jedna-neprekidnost.
Mislim,koji je smisao rješavati neodređeni integral(dakle tražiti skup svih primitivnih funkcija podintegralne funkcije) neke realne funkcije ako mi nitko ne jamči neprekidnost, jer ja imam teorem koji kaže;
da funkcija definirana na otvorenom intervalu i neprekidna ima primitivnu funkciju
,pa ja promotrim svoju funkciju i nadam se da su nam zadali neprekidnu funkciju(naravno ako nije očito da je neprekidna,a većinom nije) pa tražim primitivnu funkciju.
Ajde da još nešto pitam:
Ako treba izračunati površinu lika čija je površina iznad i ispod osi x onda se ova površina ispod osi x još množi s -1.
Razlog tome je jednostavna činjenica da ispod osi x baratamo sa negativnim vrijednosti infimuma i supremuma u podsegmentima subdivizija pa je i suma takvih negativnih brojeva(što se naravno još množe sa duljinom podsegmenta) negativna.
Upravo zato se ''napada'' minusom površina ispod grafa,jeli?
Kako bi ti ovu funkciju [x]-(x-[x]) ''imenovao'' prekidnom,a nalaziš se recimo na ispitu gdje naravno nemaš vremena čarobirati sa definicijom neprekidnosti kojom bi dokazao da je ta funkcija neprekidna(ako bi uopće dokazao).
Postoji li efektivan(brz) način da to saznam?
Ovako znam da je funkcija 'najveće cijelo' prekidna i onda onako napamet(štreberski) zaključujem da je i ova gore prekidna,a argumenta i dokaza nemam.
| Citat: | | Cini se da je tvoj problem sto pravilo pridruzivanja poistovjecujes s 'formulom'. |
Pa tako nam je rečeno.
Recimo domenu funkcije smo na analizi I definirali ovako:
Domena funkcije je skup svih vrijednosti za koje mogu obaviti sve računske operacije koje mi se u _pravilu pridruživanja_ javljaju.
| Citat: | | Kada integriras neku funkciju koja nije neprekidna... |
Znam li ja integrirati uopće išta što je prekidno osim ako ne rasparceliram funkciju na neprekidne dijelove domene ?
Ja samo znam za fundamentalan teorem,kako smo ga nazvali,koji mi omogućuje da izračunam površine određenih integrala uz potrebne pretpostavke za funkciju od kojih je jedna-neprekidnost.
Mislim,koji je smisao rješavati neodređeni integral(dakle tražiti skup svih primitivnih funkcija podintegralne funkcije) neke realne funkcije ako mi nitko ne jamči neprekidnost, jer ja imam teorem koji kaže;
da funkcija definirana na otvorenom intervalu i neprekidna ima primitivnu funkciju
,pa ja promotrim svoju funkciju i nadam se da su nam zadali neprekidnu funkciju(naravno ako nije očito da je neprekidna,a većinom nije) pa tražim primitivnu funkciju.
Ajde da još nešto pitam:
Ako treba izračunati površinu lika čija je površina iznad i ispod osi x onda se ova površina ispod osi x još množi s -1.
Razlog tome je jednostavna činjenica da ispod osi x baratamo sa negativnim vrijednosti infimuma i supremuma u podsegmentima subdivizija pa je i suma takvih negativnih brojeva(što se naravno još množe sa duljinom podsegmenta) negativna.
Upravo zato se ''napada'' minusom površina ispod grafa,jeli?
_________________
Samo sam jedan čovjek,
samo jedan pakao.
|
|
| [Vrh] |
|
veky
Forumaš(ica)
Pridružen/a: 09. 12. 2002. (19:59:43)
Postovi: (5B0)16
Lokacija: negdje daleko...
|
| Postano: 15:10 pet, 27. 8. 2004 Naslov: |
|
|
[quote="Vincent Van Ear"]Kako bi ti ovu funkciju [x]-(x-[x]) ''imenovao'' prekidnom,a nalaziš se recimo na ispitu gdje naravno nemaš vremena čarobirati sa definicijom neprekidnosti kojom bi dokazao da je ta funkcija neprekidna(ako bi uopće dokazao).[/quote]
Eh, kad ljudi ne uče teoriju s razumijevanjem :roll: ...
[quote]Postoji li efektivan(brz) način da to saznam?[/quote]
Postoji, i znaš za njega.
--SPOILER--
Da je funkcija neprekidna, imala bi limes u svakoj točki domene i on bi bio jednak funkcijskoj vrijednosti u toj točki. E sad izračunaj limes slijeva i zdesna npr. u 0 , i vidi da su različiti.
[quote]Ovako znam da je funkcija 'najveće cijelo' prekidna i onda onako napamet(štreberski) zaključujem da je i ova gore prekidna,a argumenta i dokaza nemam.[/quote]
BTW... u ovom slučaju možeš proći s razmišljanjem sličnim tvojem (ali samo sličnim!), koje ide ovako:
ako sredimo gornji izraz, dobijemo f(x)=2floor(x)-x . Iz toga izlazi floor(x)=(f(x)+x)/2 . _Kad bi_ f bila neprekidna, tad bi floor ("najveće cijelo"), kao aritmetička sredina dvije neprekidne funkcije ((identiteta je neprekidna, naravno)) bila neprekidna, a za nju znamo da nije. Dakle, pretpostavka je bila kriva, odnosno f nije neprekidna funkcija.
[quote][quote]Cini se da je tvoj problem sto pravilo pridruzivanja poistovjecujes s 'formulom'.[/quote]
Pa tako nam je rečeno.
Recimo domenu funkcije smo na analizi I definirali ovako:
Domena funkcije je skup svih vrijednosti za koje mogu obaviti sve računske operacije koje mi se u _pravilu pridruživanja_ javljaju.[/quote]
Smijem pitat tko je to tako definirao?
[quote]Znam li ja integrirati uopće išta što je prekidno osim ako ne rasparceliram funkciju na neprekidne dijelove domene ?[/quote]
Jako dobro pitanje. :-)
Mislim da ipak znaš. Za Cantorov skup si čuo?
Probaj integrirati njegovu karakterističnu funkciju. ;-)
[quote]Ja samo znam za fundamentalan teorem,kako smo ga nazvali,koji mi omogućuje da izračunam površine određenih integrala[/quote]
_površine određenih integrala_??
Iznose integrala. Oni su površine samo u specijalnim slučajevima, a i tad nisu površine _integrala_, već nečeg drugog (dijelova ravnine, npr.).
[quote] uz potrebne pretpostavke za funkciju od kojih je jedna-neprekidnost.[/quote]
Uvijek znaš i za definiciju ;-)
(koja baš i nije operativna, ali dâ se ponekad iskoristiti).
[quote]Mislim,koji je smisao rješavati neodređeni integral(dakle tražiti skup svih primitivnih funkcija podintegralne funkcije) neke realne funkcije ako mi nitko ne jamči neprekidnost, jer ja imam teorem koji kaže;
da funkcija definirana na otvorenom intervalu i neprekidna ima primitivnu funkciju
,pa ja promotrim svoju funkciju i nadam se da su nam zadali neprekidnu funkciju(naravno ako nije očito da je neprekidna,a većinom nije)[/quote]
Naprotiv.
Ako je funkcija zadana multipozicijom (think "kompozicijom") osnovnih računskih operacijâ iz elementarnih funkcijâ, tada je prilično očito da je neprekidna.
[quote]Ako treba izračunati površinu lika čija je površina iznad i ispod osi x onda se ova površina ispod osi x još množi s -1.
Razlog tome je jednostavna činjenica da ispod osi x baratamo sa negativnim vrijednosti infimuma i supremuma u podsegmentima subdivizija pa je i suma takvih negativnih brojeva(što se naravno još množe sa duljinom podsegmenta) negativna.
Upravo zato se ''napada'' minusom površina ispod grafa,jeli?[/quote]
Kao što rekoh gore, integral je jedno, a površina drugo. Oni su "jednaki" samo pod izvjesnim pretpostavkama, jedna od kojih (iako nipošto ne jedina) je da je funkcija nenegativna, odnosno graf joj je iznad osi x .
S druge strane, naravno, ako uzmeš umjesto f funkciju -f , integral će postati suprotan, funkcija će postati nepozitivna, a "površina" će ostati ista, samo primijeti da to više nije površina _ispod_ grafa od f i _iznad_ osi x , već je _iznad_ grafa od f i _ispod_ osi x . U ovom svjetlu, prilično je logično da joj se promijeni predznak, zar ne? ;-)
[color=blue]Veky, znas pravila Foruma: suzdrzi se od prostackih zargonizama![/color] :evil: | Vincent Van Ear (napisa): | | Kako bi ti ovu funkciju [x]-(x-[x]) ''imenovao'' prekidnom,a nalaziš se recimo na ispitu gdje naravno nemaš vremena čarobirati sa definicijom neprekidnosti kojom bi dokazao da je ta funkcija neprekidna(ako bi uopće dokazao). |
Eh, kad ljudi ne uče teoriju s razumijevanjem  ...
| Citat: | | Postoji li efektivan(brz) način da to saznam? |
Postoji, i znaš za njega.
–SPOILER–
Da je funkcija neprekidna, imala bi limes u svakoj točki domene i on bi bio jednak funkcijskoj vrijednosti u toj točki. E sad izračunaj limes slijeva i zdesna npr. u 0 , i vidi da su različiti.
| Citat: | | Ovako znam da je funkcija 'najveće cijelo' prekidna i onda onako napamet(štreberski) zaključujem da je i ova gore prekidna,a argumenta i dokaza nemam. |
BTW... u ovom slučaju možeš proći s razmišljanjem sličnim tvojem (ali samo sličnim!), koje ide ovako:
ako sredimo gornji izraz, dobijemo f(x)=2floor(x)-x . Iz toga izlazi floor(x)=(f(x)+x)/2 . _Kad bi_ f bila neprekidna, tad bi floor ("najveće cijelo"), kao aritmetička sredina dvije neprekidne funkcije ((identiteta je neprekidna, naravno)) bila neprekidna, a za nju znamo da nije. Dakle, pretpostavka je bila kriva, odnosno f nije neprekidna funkcija.
| Citat: | | Citat: | | Cini se da je tvoj problem sto pravilo pridruzivanja poistovjecujes s 'formulom'. |
Pa tako nam je rečeno.
Recimo domenu funkcije smo na analizi I definirali ovako:
Domena funkcije je skup svih vrijednosti za koje mogu obaviti sve računske operacije koje mi se u _pravilu pridruživanja_ javljaju. |
Smijem pitat tko je to tako definirao?
| Citat: | | Znam li ja integrirati uopće išta što je prekidno osim ako ne rasparceliram funkciju na neprekidne dijelove domene ? |
Jako dobro pitanje.
Mislim da ipak znaš. Za Cantorov skup si čuo?
Probaj integrirati njegovu karakterističnu funkciju.
| Citat: | | Ja samo znam za fundamentalan teorem,kako smo ga nazvali,koji mi omogućuje da izračunam površine određenih integrala |
_površine određenih integrala_??
Iznose integrala. Oni su površine samo u specijalnim slučajevima, a i tad nisu površine _integrala_, već nečeg drugog (dijelova ravnine, npr.).
| Citat: | | uz potrebne pretpostavke za funkciju od kojih je jedna-neprekidnost. |
Uvijek znaš i za definiciju
(koja baš i nije operativna, ali dâ se ponekad iskoristiti).
| Citat: | Mislim,koji je smisao rješavati neodređeni integral(dakle tražiti skup svih primitivnih funkcija podintegralne funkcije) neke realne funkcije ako mi nitko ne jamči neprekidnost, jer ja imam teorem koji kaže;
da funkcija definirana na otvorenom intervalu i neprekidna ima primitivnu funkciju
,pa ja promotrim svoju funkciju i nadam se da su nam zadali neprekidnu funkciju(naravno ako nije očito da je neprekidna,a većinom nije) |
Naprotiv.
Ako je funkcija zadana multipozicijom (think "kompozicijom") osnovnih računskih operacijâ iz elementarnih funkcijâ, tada je prilično očito da je neprekidna.
| Citat: | Ako treba izračunati površinu lika čija je površina iznad i ispod osi x onda se ova površina ispod osi x još množi s -1.
Razlog tome je jednostavna činjenica da ispod osi x baratamo sa negativnim vrijednosti infimuma i supremuma u podsegmentima subdivizija pa je i suma takvih negativnih brojeva(što se naravno još množe sa duljinom podsegmenta) negativna.
Upravo zato se ''napada'' minusom površina ispod grafa,jeli? |
Kao što rekoh gore, integral je jedno, a površina drugo. Oni su "jednaki" samo pod izvjesnim pretpostavkama, jedna od kojih (iako nipošto ne jedina) je da je funkcija nenegativna, odnosno graf joj je iznad osi x .
S druge strane, naravno, ako uzmeš umjesto f funkciju -f , integral će postati suprotan, funkcija će postati nepozitivna, a "površina" će ostati ista, samo primijeti da to više nije površina _ispod_ grafa od f i _iznad_ osi x , već je _iznad_ grafa od f i _ispod_ osi x . U ovom svjetlu, prilično je logično da joj se promijeni predznak, zar ne?
Veky, znas pravila Foruma: suzdrzi se od prostackih zargonizama! 
|
|
| [Vrh] |
|
Vincent Van Ear
Forumaš(ica)
Pridružen/a: 19. 08. 2004. (11:29:05)
Postovi: (175)16
|
| Postano: 16:01 pet, 27. 8. 2004 Naslov: |
|
|
|
[quote]Eh, kad ljudi ne uče teoriju s razumijevanjem ...[/quote]
Istina,ali to ti nitko(sorry zbog generalizacija) neće učiniti,svi će odmah bjesmučno tehnicirati.
[quote]Smijem pitat tko je to tako definirao?[/quote]
Prof H.Šikić na predavanjima,sada nigdje u okolini te rečenice ne piše da je to definicija.Ne sjećam se baš najbolje ali možda sam ja to napisao onako dok je on govorio.Ma ne mogu se pritužiti na profesore koji je stvarno uvijek precizan,to sam ja valjda prepisao njegov slang.
Izuzev preciznosti što uopće fali toj definiciji,baš je zgodna.
[quote]Mislim da ipak znaš. Za Cantorov skup si čuo?[/quote]
Za Cantorov teorem da ali skup ne.
[quote]_površine određenih integrala_??
Iznose integrala. [/quote]
Aha,opet nedostatak preciznosti s moje strane jeli?
Ispravio si me zato jer površina ne može biti negativan broj.
[quote]Oni su površine samo u specijalnim slučajevima[/quote]
A te slučajeve imam uvijek ukoliko prije računanja iznosa integrala neke funkcije istu ''napadnem'' sa funkcijom apsolutne vrijednosti što _smijem_ učiniti,to mi jamči propozicija(P12/1 ) koja kaže da uz prave pretpostavke naravno,Reiman integrabilnost funkcije f jamči i Reiman integrabilnost funkcije |f|.
I doista,želi li se dobiti korektna površina ispod grafa funkcije,funkcija se odmah na početku mora ''napasti'' funkcijom apsolutne vrijednosti i zatim primijeniti tehnike integriranja jer u protivnom dobivamo:
|aSb f(x)dx| <= aSb |f|(x)dx ,dakle dobit ćemo manji iznos površine no što je on zapravo.
[quote]Uvijek znaš i za definiciju
(koja baš i nije operativna, ali dâ se ponekad iskoristiti).[/guote]
Zato i je tu ''gospodin'' kriterij.:O)
[quote]Ako je funkcija zadana multipozicijom (think "kompozicijom") osnovnih računskih operacijâ iz elementarnih funkcijâ, tada je prilično očito da je neprekidna.[/quote]
Ma ja bježim od ''očitosti'' jer sam često slijep(a opet često ne mogu drugačije nešto argumentirati nego lijeno reći-to mi je očito,logično,podrazumjeva se…you name it),znaš što se više bakćem s matematikom shvaćam da mi oči nisu uopće potrebne i da bi bilo sasvim dovoljno biti kao Euler,biti lišen svih mogućih vizualnih interferencija usredotočen na misao i dodir,a opet naravno sljepoća je ipak hendikep…
A kako je tebi to uopće očito,iskustvo ili?
[quote]Kao što rekoh gore, integral je jedno, a površina drugo. Oni su "jednaki" samo pod izvjesnim pretpostavkama, jedna od kojih (iako nipošto ne jedina) je da je funkcija nenegativna, odnosno graf joj je iznad osi x .
S druge strane, naravno, ako uzmeš umjesto f funkciju -f , integral će postati suprotan, funkcija će postati nepozitivna, a "površina" će ostati ista, samo primijeti da to više nije površina _ispod_ grafa od f i _iznad_ osi x , već je _iznad_ grafa od f i _ispod_ osi x . U ovom svjetlu, prilično je logično da joj se promijeni predznak, zar ne? [/quote]
Odlično.;))
| Citat: | | Eh, kad ljudi ne uče teoriju s razumijevanjem ... |
Istina,ali to ti nitko(sorry zbog generalizacija) neće učiniti,svi će odmah bjesmučno tehnicirati.
| Citat: | | Smijem pitat tko je to tako definirao? |
Prof H.Šikić na predavanjima,sada nigdje u okolini te rečenice ne piše da je to definicija.Ne sjećam se baš najbolje ali možda sam ja to napisao onako dok je on govorio.Ma ne mogu se pritužiti na profesore koji je stvarno uvijek precizan,to sam ja valjda prepisao njegov slang.
Izuzev preciznosti što uopće fali toj definiciji,baš je zgodna.
| Citat: | | Mislim da ipak znaš. Za Cantorov skup si čuo? |
Za Cantorov teorem da ali skup ne.
| Citat: | _površine određenih integrala_??
Iznose integrala. |
Aha,opet nedostatak preciznosti s moje strane jeli?
Ispravio si me zato jer površina ne može biti negativan broj.
| Citat: | | Oni su površine samo u specijalnim slučajevima |
A te slučajeve imam uvijek ukoliko prije računanja iznosa integrala neke funkcije istu ''napadnem'' sa funkcijom apsolutne vrijednosti što _smijem_ učiniti,to mi jamči propozicija(P12/1 ) koja kaže da uz prave pretpostavke naravno,Reiman integrabilnost funkcije f jamči i Reiman integrabilnost funkcije |f|.
I doista,želi li se dobiti korektna površina ispod grafa funkcije,funkcija se odmah na početku mora ''napasti'' funkcijom apsolutne vrijednosti i zatim primijeniti tehnike integriranja jer u protivnom dobivamo:
|aSb f(x)dx| ⇐ aSb |f|(x)dx ,dakle dobit ćemo manji iznos površine no što je on zapravo.
[quote]Uvijek znaš i za definiciju
(koja baš i nije operativna, ali dâ se ponekad iskoristiti).[/guote]
Zato i je tu ''gospodin'' kriterij.:O)
| Citat: | | Ako je funkcija zadana multipozicijom (think "kompozicijom") osnovnih računskih operacijâ iz elementarnih funkcijâ, tada je prilično očito da je neprekidna. |
Ma ja bježim od ''očitosti'' jer sam često slijep(a opet često ne mogu drugačije nešto argumentirati nego lijeno reći-to mi je očito,logično,podrazumjeva se…you name it),znaš što se više bakćem s matematikom shvaćam da mi oči nisu uopće potrebne i da bi bilo sasvim dovoljno biti kao Euler,biti lišen svih mogućih vizualnih interferencija usredotočen na misao i dodir,a opet naravno sljepoća je ipak hendikep…
A kako je tebi to uopće očito,iskustvo ili?
| Citat: | Kao što rekoh gore, integral je jedno, a površina drugo. Oni su "jednaki" samo pod izvjesnim pretpostavkama, jedna od kojih (iako nipošto ne jedina) je da je funkcija nenegativna, odnosno graf joj je iznad osi x .
S druge strane, naravno, ako uzmeš umjesto f funkciju -f , integral će postati suprotan, funkcija će postati nepozitivna, a "površina" će ostati ista, samo primijeti da to više nije površina _ispod_ grafa od f i _iznad_ osi x , već je _iznad_ grafa od f i _ispod_ osi x . U ovom svjetlu, prilično je logično da joj se promijeni predznak, zar ne? |
Odlično.)
_________________
Samo sam jedan čovjek,
samo jedan pakao.
|
|
| [Vrh] |
|
ZELENIZUBNAPLANETIDO
SADE
Forumaš(ica)
Pridružen/a: 04. 03. 2004. (19:56:15)
Postovi: (54F)16
Lokacija: hm?
|
| Postano: 20:25 pet, 27. 8. 2004 Naslov: |
|
|
|
[quote="Vincent Van Ear"]Istina,ali to ti nitko(sorry zbog generalizacija) neće učiniti,svi će odmah bjesmučno tehnicirati.[/quote]
"Tehniciranje" je korisno za trazenje "precaca" do rijesenja, ali nikako ne moze biti zamjena dokazu. :ccc:
[quote="Vincent Van Ear"]Prof H.Šikić na predavanjima,sada nigdje u okolini te rečenice ne piše da je to definicija.Ne sjećam se baš najbolje ali možda sam ja to napisao onako dok je on govorio.Ma ne mogu se pritužiti na profesore koji je stvarno uvijek precizan,to sam ja valjda prepisao njegov slang.
Izuzev preciznosti što uopće fali toj definiciji,baš je zgodna.[/quote]
:shock: to o cemu ti pricas je prirodno podrucje definicije (tj. najveca moguca domena fje sa obzirom na definirano "pravilo preslikavanja"), domena fje je nesto sasvim drugo :shock: (proizvoljni skup brojeva, vektora, carapa i sl) i _NIKADA_ brkat to dvoje ako mislis proci kroz analize :roll:
[quote="Vincent Van Ear"]I doista,želi li se dobiti korektna površina ispod grafa funkcije,funkcija se odmah na početku mora ''napasti'' funkcijom apsolutne vrijednosti i zatim primijeniti tehnike integriranja jer u protivnom dobivamo:
|aSb f(x)dx| <= aSb |f|(x)dx ,dakle dobit ćemo manji iznos površine no što je on zapravo.[/quote]
Da... to je nesto sto bih volio zvati povrsinom...
[quote="Vincent Van Ear"]Ma ja bježim od ''očitosti'' jer sam često slijep(a opet često ne mogu drugačije nešto argumentirati nego lijeno reći-to mi je očito,logično,podrazumjeva se…you name it)[/quote]
Pa ocito je u smislu trivijalnosti sa obzirom na stvari naucene na MA1. Rekli ste: suma, razlika, produkt, kvocijent i kompozicija konacnog broja neprekidnih fja jest neprekidna fja. Sa druge strane, dokazali ste i neprekidnost elementarnih fja, ergo: .... :)
[quote="Vincent Van Ear"]znaš što se više bakćem s matematikom shvaćam da mi oči nisu uopće potrebne i da bi bilo sasvim dovoljno biti kao Euler,biti lišen svih mogućih vizualnih interferencija usredotočen na misao i dodir,a opet naravno sljepoća je ipak hendikep…
A kako je tebi to uopće očito,iskustvo ili?[/quote]
Do formalnog dokaza BW teorema, i ti si vjerovatno "slutio" da , ukoliko neprekidna fja definirana na segmentu ima pozitivne i negativne fjske vrijednosti, da tada ona, negdje izmedju ima nultocku, i to je bilo "ocito", iako nikako trivijalno. Sada kada naletim na takvu nekaku propoziciju, ona je intuitivno jasna i "slutim" da je istinita, dapace, "slutim" i zasto, iako ju nikako ne bih nazvao "ocitom" buduci da je krajnje netrivijalna i trebali bi tjedni da shvatim sto je pisac htio reci kada ih je dokazao (npr. Jordanov teorem (ugrubo, kontura (injektivan zatvoren put u ravnini, npr kruznica) dijeli ravninu na dva disjunktna podrucja) ).
Iako je tesko, ako ne i malo glupo, generalizirati ovakve, .. dojmove. Al eto, sretno :)
| Vincent Van Ear (napisa): | | Istina,ali to ti nitko(sorry zbog generalizacija) neće učiniti,svi će odmah bjesmučno tehnicirati. |
"Tehniciranje" je korisno za trazenje "precaca" do rijesenja, ali nikako ne moze biti zamjena dokazu. 
| Vincent Van Ear (napisa): | Prof H.Šikić na predavanjima,sada nigdje u okolini te rečenice ne piše da je to definicija.Ne sjećam se baš najbolje ali možda sam ja to napisao onako dok je on govorio.Ma ne mogu se pritužiti na profesore koji je stvarno uvijek precizan,to sam ja valjda prepisao njegov slang.
Izuzev preciznosti što uopće fali toj definiciji,baš je zgodna. |
 to o cemu ti pricas je prirodno podrucje definicije (tj. najveca moguca domena fje sa obzirom na definirano "pravilo preslikavanja"), domena fje je nesto sasvim drugo (proizvoljni skup brojeva, vektora, carapa i sl) i _NIKADA_ brkat to dvoje ako mislis proci kroz analize
| Vincent Van Ear (napisa): | I doista,želi li se dobiti korektna površina ispod grafa funkcije,funkcija se odmah na početku mora ''napasti'' funkcijom apsolutne vrijednosti i zatim primijeniti tehnike integriranja jer u protivnom dobivamo:
|aSb f(x)dx| ⇐ aSb |f|(x)dx ,dakle dobit ćemo manji iznos površine no što je on zapravo. |
Da... to je nesto sto bih volio zvati povrsinom...
| Vincent Van Ear (napisa): | | Ma ja bježim od ''očitosti'' jer sam često slijep(a opet često ne mogu drugačije nešto argumentirati nego lijeno reći-to mi je očito,logično,podrazumjeva se…you name it) |
Pa ocito je u smislu trivijalnosti sa obzirom na stvari naucene na MA1. Rekli ste: suma, razlika, produkt, kvocijent i kompozicija konacnog broja neprekidnih fja jest neprekidna fja. Sa druge strane, dokazali ste i neprekidnost elementarnih fja, ergo: ....
| Vincent Van Ear (napisa): | znaš što se više bakćem s matematikom shvaćam da mi oči nisu uopće potrebne i da bi bilo sasvim dovoljno biti kao Euler,biti lišen svih mogućih vizualnih interferencija usredotočen na misao i dodir,a opet naravno sljepoća je ipak hendikep…
A kako je tebi to uopće očito,iskustvo ili? |
Do formalnog dokaza BW teorema, i ti si vjerovatno "slutio" da , ukoliko neprekidna fja definirana na segmentu ima pozitivne i negativne fjske vrijednosti, da tada ona, negdje izmedju ima nultocku, i to je bilo "ocito", iako nikako trivijalno. Sada kada naletim na takvu nekaku propoziciju, ona je intuitivno jasna i "slutim" da je istinita, dapace, "slutim" i zasto, iako ju nikako ne bih nazvao "ocitom" buduci da je krajnje netrivijalna i trebali bi tjedni da shvatim sto je pisac htio reci kada ih je dokazao (npr. Jordanov teorem (ugrubo, kontura (injektivan zatvoren put u ravnini, npr kruznica) dijeli ravninu na dva disjunktna podrucja) ).
Iako je tesko, ako ne i malo glupo, generalizirati ovakve, .. dojmove. Al eto, sretno
_________________ 
Pupoljak nije negiran. Rekao sam to i ponovit cu to jos jedanput. Pupoljak NIJE negirAn.
MADD
(Mothers Against Dirty Dialectics)
Based on a true story. NOT.
Ko ih sljivi, mi sviramo punk |
|
| [Vrh] |
|
Vincent Van Ear
Forumaš(ica)
Pridružen/a: 19. 08. 2004. (11:29:05)
Postovi: (175)16
|
| Postano: 23:05 pet, 27. 8. 2004 Naslov: |
|
|
|
Hvala na opaskama,e sad imam jednu sitnu mušicu na ovom teoremu:
[color=green]Teorem:
Pretpostavke:f:I->IR,I-otvoreni interval podskup od IR,f neprekidna.
Doprinos teorema:ima primitivnu funkciju.[/color]
Dokaz:
a@I fiksan
Ax@I def. F(x):=aSx f(t)dt ( aSb je oznaka za integral u području od a do x)
Primjetimo da taj integral doista postoji jer je f sada na segmentu[a,x] i neprekidna po pretpostavci pa Reimanov teorem kaže da je takva funkcija integrabilna.
Novo definirana funkcija F crpi elemente domene iz I,a vrijednosti šalje u IR(određeni integral je realan broj) pa vrijedi:
F:I->IR
Ok,sada još moramo dokazati da je F diferencijabilna na svojoj domeni i da joj je derivacija jednaka funkciji f :
Uzmimo c@I i promotrimo razliku:
F(x)-F(c)=po def. od F=aSx f(t)dt – aSc f(t)dt = cSa f(t)dt + aSx f(t)dt = cSx f(t)dt
cSx f(t)dt = cSa f(t)dt + aSx f(t)dt
Naša funkcija je neprekidna => po Reimanovom teoremu => postoji točka v@[color=brown]<[/color]c,x[color=brown]>[/color] takva da vrijedi cSx f(t)dt=f(v)*(x-c)
[color=brown](Moje pitanje:
Reiman kaže da postoji v@[c,x] takva da vrijedi…dali su ovdje gore rubne točke isključene jer:
Za točku c se to trivijalno vidi pa ako smo eto maknuli c pa čemo onda maknuti i x da nas ne zbunjuje?
I ako je zbog toga zašto se to ne naglasi makar bila trivijalnost?
Jer ako u matematici vrijedi ona:'čitaj kako piše' onda neka piše kako treba da ja mogu bezprekidno čitati…mah… )[/color]
=> F(x)-F(c)=f(v)*(x-c) x=!c /: (x-c)
F(x)-F(c)/x-c = f(v) lim_{x->c}
f je neprekidna => Teorem:funkcija je neprekidna u c akko postoji limes u c i jednak je f(c)=>postoji lim u c=f(c) tj. postoji derivacija F'(c) i F'(c)=f(c)
Q-E.D
Može razrješenje i ove dileme :) :
Trebam integrirati funkciju 'najveće cijelo' u području od 1 do 2.
Kako ja to znam integrirati kada je ona _na segmentu_ od 1 do 2 _neprekidna_,točnije neprekidna je u rubnoj točki 2 slijeva ?
Gledajući sliku meni je jasno da je površina jednaka 1 jer se radi o jediničnom kvadratu ali analitički mi nije jasno.
Fundamentalan teorem dozvoljava uporabu Newton-Leibnitzove formule samo za funkcije definirane _na segmentu_ i _neprekidne_ koje naravno imaju primitivnu funkciju,a bez njega ja neznam dobiti konkretan iznos za integral,ma bez domene koja je segment i omeđena ja neznam ništa jer smo upravo samo za takvu klasu općih omeđenih funkcija definirali Reiman integrabilnost.
Hvala na opaskama,e sad imam jednu sitnu mušicu na ovom teoremu:
Teorem:
Pretpostavke:f:I→IR,I-otvoreni interval podskup od IR,f neprekidna.
Doprinos teorema:ima primitivnu funkciju.
Dokaz:
a@I fiksan
Ax@I def. F(x):=aSx f(t)dt ( aSb je oznaka za integral u području od a do x)
Primjetimo da taj integral doista postoji jer je f sada na segmentu[a,x] i neprekidna po pretpostavci pa Reimanov teorem kaže da je takva funkcija integrabilna.
Novo definirana funkcija F crpi elemente domene iz I,a vrijednosti šalje u IR(određeni integral je realan broj) pa vrijedi:
F:I→IR
Ok,sada još moramo dokazati da je F diferencijabilna na svojoj domeni i da joj je derivacija jednaka funkciji f :
Uzmimo c@I i promotrimo razliku:
F(x)-F(c)=po def. od F=aSx f(t)dt – aSc f(t)dt = cSa f(t)dt + aSx f(t)dt = cSx f(t)dt
cSx f(t)dt = cSa f(t)dt + aSx f(t)dt
Naša funkcija je neprekidna ⇒ po Reimanovom teoremu ⇒ postoji točka v@<c,x> takva da vrijedi cSx f(t)dt=f(v)*(x-c)
(Moje pitanje:
Reiman kaže da postoji v@[c,x] takva da vrijedi…dali su ovdje gore rubne točke isključene jer:
Za točku c se to trivijalno vidi pa ako smo eto maknuli c pa čemo onda maknuti i x da nas ne zbunjuje?
I ako je zbog toga zašto se to ne naglasi makar bila trivijalnost?
Jer ako u matematici vrijedi ona:'čitaj kako piše' onda neka piše kako treba da ja mogu bezprekidno čitati…mah… )
⇒ F(x)-F(c)=f(v)*(x-c) x=!c /: (x-c)
F(x)-F(c)/x-c = f(v) lim_{x→c}
f je neprekidna ⇒ Teorem:funkcija je neprekidna u c akko postoji limes u c i jednak je f(c)⇒postoji lim u c=f(c) tj. postoji derivacija F'(c) i F'(c)=f(c)
Q-E.D
Može razrješenje i ove dileme :
Trebam integrirati funkciju 'najveće cijelo' u području od 1 do 2.
Kako ja to znam integrirati kada je ona _na segmentu_ od 1 do 2 _neprekidna_,točnije neprekidna je u rubnoj točki 2 slijeva ?
Gledajući sliku meni je jasno da je površina jednaka 1 jer se radi o jediničnom kvadratu ali analitički mi nije jasno.
Fundamentalan teorem dozvoljava uporabu Newton-Leibnitzove formule samo za funkcije definirane _na segmentu_ i _neprekidne_ koje naravno imaju primitivnu funkciju,a bez njega ja neznam dobiti konkretan iznos za integral,ma bez domene koja je segment i omeđena ja neznam ništa jer smo upravo samo za takvu klasu općih omeđenih funkcija definirali Reiman integrabilnost.
_________________
Samo sam jedan čovjek,
samo jedan pakao.
|
|
| [Vrh] |
|
mdoko
Forumaš(ica)
Pridružen/a: 30. 11. 2002. (22:17:12)
Postovi: (71A)16
Spol:
Lokacija: Heriot-Watt University, Edinburgh
|
| Postano: 23:33 pet, 27. 8. 2004 Naslov: |
|
|
|
[quote="Vincent Van Ear"](Moje pitanje:
Reiman kaže da postoji v@[c,x] takva da vrijedi…dali su ovdje gore rubne točke isključene jer:
Za točku c se to trivijalno vidi pa ako smo eto maknuli c pa čemo onda maknuti i x da nas ne zbunjuje?[/quote]
Cekaj malo, zasto ne bi moglo biti v=c? :shock:
Za funkciju najvece cijelo na segmentu [1,2] je u svim tockama skupa [1,2> jednaka 1, a u 2 poprima vrijednost 2. Iz kriterija integrabilnosti i definicije integrala jednostavno je dokazati da ako se funkcije f i g razlikuju u konacno ili prebrojivo mnogo tocaka onda su im integrali jednaki (pokusaj).
[i]Comment: vrijedi i opcenitija tvrdnja, ali cini mi se da ovdje nije mjesto za to.[/i]
Dakle, nalazis se u situaciji da integriras funkciju f(x)=1 na segmentu [1,2], a taj integral ocito iznosi 1. OK?
Jos samo ovo: funkcija f: [1,2] -> |R, f(x) = floor(x) _nije_ neprekidna s lijeva u tocki 2 :!:
| Vincent Van Ear (napisa): | (Moje pitanje:
Reiman kaže da postoji v@[c,x] takva da vrijedi…dali su ovdje gore rubne točke isključene jer:
Za točku c se to trivijalno vidi pa ako smo eto maknuli c pa čemo onda maknuti i x da nas ne zbunjuje? |
Cekaj malo, zasto ne bi moglo biti v=c?
Za funkciju najvece cijelo na segmentu [1,2] je u svim tockama skupa [1,2> jednaka 1, a u 2 poprima vrijednost 2. Iz kriterija integrabilnosti i definicije integrala jednostavno je dokazati da ako se funkcije f i g razlikuju u konacno ili prebrojivo mnogo tocaka onda su im integrali jednaki (pokusaj).
Comment: vrijedi i opcenitija tvrdnja, ali cini mi se da ovdje nije mjesto za to.
Dakle, nalazis se u situaciji da integriras funkciju f(x)=1 na segmentu [1,2], a taj integral ocito iznosi 1. OK?
Jos samo ovo: funkcija f: [1,2] → |R, f(x) = floor(x) _nije_ neprekidna s lijeva u tocki 2 
_________________
Extraordinary claims require extraordinary evidence. – Carl Sagan
|
|
| [Vrh] |
|
Vincent Van Ear
Forumaš(ica)
Pridružen/a: 19. 08. 2004. (11:29:05)
Postovi: (175)16
|
| Postano: 23:58 pet, 27. 8. 2004 Naslov: |
|
|
|
[quote]Cekaj malo, zasto ne bi moglo biti v=c? [/quote]
To i mene mori!
[quote]Za funkciju najvece cijelo na segmentu [1,2] je u svim tockama skupa [1,2> jednaka 1, a u 2 poprima vrijednost 2.
Iz kriterija integrabilnosti i definicije integrala jednostavno je dokazati da ako se funkcije f i g razlikuju u konacno ili prebrojivo mnogo tocaka onda su im integrali jednaki (pokusaj). [/quote]
Zar ja nemam neprebrojivo mnogo točaka na segmentu ?
[quote]Comment: vrijedi i opcenitija tvrdnja, ali cini mi se da ovdje nije mjesto za to.
Dakle, nalazis se u situaciji da integriras funkciju f(x)=1 na segmentu [1,2], a taj integral ocito iznosi 1. OK? [/quote]
Zašto je tako nešto profesor uopće prešutio?
[quote]Jos samo ovo: funkcija f: [1,2] -> |R, f(x) = floor(x) _nije_ neprekidna s lijeva u tocki 2[/quote]
Fala,tipfeler-htjede reći da je prekidna s lijeva u 2.
| Citat: | | Cekaj malo, zasto ne bi moglo biti v=c? |
To i mene mori!
| Citat: | Za funkciju najvece cijelo na segmentu [1,2] je u svim tockama skupa [1,2> jednaka 1, a u 2 poprima vrijednost 2.
Iz kriterija integrabilnosti i definicije integrala jednostavno je dokazati da ako se funkcije f i g razlikuju u konacno ili prebrojivo mnogo tocaka onda su im integrali jednaki (pokusaj). |
Zar ja nemam neprebrojivo mnogo točaka na segmentu ?
| Citat: | Comment: vrijedi i opcenitija tvrdnja, ali cini mi se da ovdje nije mjesto za to.
Dakle, nalazis se u situaciji da integriras funkciju f(x)=1 na segmentu [1,2], a taj integral ocito iznosi 1. OK? |
Zašto je tako nešto profesor uopće prešutio?
| Citat: | | Jos samo ovo: funkcija f: [1,2] -> |R, f(x) = floor(x) _nije_ neprekidna s lijeva u tocki 2 |
Fala,tipfeler-htjede reći da je prekidna s lijeva u 2.
_________________
Samo sam jedan čovjek,
samo jedan pakao.
|
|
| [Vrh] |
|
ZELENIZUBNAPLANETIDO
SADE
Forumaš(ica)
Pridružen/a: 04. 03. 2004. (19:56:15)
Postovi: (54F)16
Lokacija: hm?
|
| Postano: 9:47 sub, 28. 8. 2004 Naslov: |
|
|
|
[quote="Vincent Van Ear"][quote]Cekaj malo, zasto ne bi moglo biti v=c?
To i mene mori![/quote]
[/quote]
Mozebit da se profesor malo zaletio na predavanju. (Barem ja) nisam nasao problem u daljnjem tijeku dokaza u slucaju da je v=c :-k. Sa druge strane, lako mi je zamisliti da i iskusna osoba napravi taj feller jer, nakon sto dokazemo tu propoziciju, lako je dokazati da taj v uistinu jest iz <x,c> a ne [x,c], ali kao poslijedica Lagrangeovog teorema, koji PRETPOSTAVLJA diferencijabilnost a ne Riemannovog :?
(tj. ako tokom dokaza nesto podsvijesno pretpostavis, pogotovo ako je to ono sto pokusavas dokazati, onda je sva prilika da ces to i dokazati :g: iako to ovdje nije slucaj)
[quote="Vincent Van Ear"][quote]Za funkciju najvece cijelo na segmentu [1,2] je u svim tockama skupa [1,2> jednaka 1, a u 2 poprima vrijednost 2.
Iz kriterija integrabilnosti i definicije integrala jednostavno je dokazati da ako se funkcije f i g razlikuju u samo konacno ili prebrojivo mnogo tocaka onda su im integrali jednaki (pokusaj). [/quote]
Zar ja nemam neprebrojivo mnogo točaka na segmentu ?[/quote]
Imas ;) ali ako se dvije fje razlikuju u samo konacnom ili prebrojivom broju tocaka, tada ce im integrali biti jednaki ;)
Probaj dokazati (hint: ako se fje f i g razlikuju u konacnom/prebrojivom broju tocaka tada skup [latex](f-g)^{-1}( R / \{0\})[/latex] ne sadrzi niti jedan interval)
[quote="Vincent Van Ear"][quote]Comment: vrijedi i opcenitija tvrdnja, ali cini mi se da ovdje nije mjesto za to.
Dakle, nalazis se u situaciji da integriras funkciju f(x)=1 na segmentu [1,2], a taj integral ocito iznosi 1. OK? [/quote]
Zašto je tako nešto profesor uopće prešutio?[/quote]
Mislim da nije...... bar nije u "nase vrijeme" :lol:, poprilicno se dobro sijecam da je izrecena barem ona gornja tvrdnja o fji sa konacnim/prebrojivim brojem ne-nul :) tocaka :) (trivijalna poslijedica cije je, ovo o cemu doko prica)
| Vincent Van Ear (napisa): | | Citat: | Cekaj malo, zasto ne bi moglo biti v=c?
To i mene mori! |
|
Mozebit da se profesor malo zaletio na predavanju. (Barem ja) nisam nasao problem u daljnjem tijeku dokaza u slucaju da je v=c  . Sa druge strane, lako mi je zamisliti da i iskusna osoba napravi taj feller jer, nakon sto dokazemo tu propoziciju, lako je dokazati da taj v uistinu jest iz <x,c> a ne [x,c], ali kao poslijedica Lagrangeovog teorema, koji PRETPOSTAVLJA diferencijabilnost a ne Riemannovog 
(tj. ako tokom dokaza nesto podsvijesno pretpostavis, pogotovo ako je to ono sto pokusavas dokazati, onda je sva prilika da ces to i dokazati  iako to ovdje nije slucaj)
| Vincent Van Ear (napisa): | | Citat: | Za funkciju najvece cijelo na segmentu [1,2] je u svim tockama skupa [1,2> jednaka 1, a u 2 poprima vrijednost 2.
Iz kriterija integrabilnosti i definicije integrala jednostavno je dokazati da ako se funkcije f i g razlikuju u samo konacno ili prebrojivo mnogo tocaka onda su im integrali jednaki (pokusaj). |
Zar ja nemam neprebrojivo mnogo točaka na segmentu ? |
Imas ali ako se dvije fje razlikuju u samo konacnom ili prebrojivom broju tocaka, tada ce im integrali biti jednaki
Probaj dokazati (hint: ako se fje f i g razlikuju u konacnom/prebrojivom broju tocaka tada skup 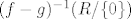 ne sadrzi niti jedan interval)
| Vincent Van Ear (napisa): | | Citat: | Comment: vrijedi i opcenitija tvrdnja, ali cini mi se da ovdje nije mjesto za to.
Dakle, nalazis se u situaciji da integriras funkciju f(x)=1 na segmentu [1,2], a taj integral ocito iznosi 1. OK? |
Zašto je tako nešto profesor uopće prešutio? |
Mislim da nije...... bar nije u "nase vrijeme"  , poprilicno se dobro sijecam da je izrecena barem ona gornja tvrdnja o fji sa konacnim/prebrojivim brojem ne-nul tocaka (trivijalna poslijedica cije je, ovo o cemu doko prica)
_________________
Pupoljak nije negiran. Rekao sam to i ponovit cu to jos jedanput. Pupoljak NIJE negirAn.
MADD
(Mothers Against Dirty Dialectics)
Based on a true story. NOT.
Ko ih sljivi, mi sviramo punk |
|
| [Vrh] |
|
Vincent Van Ear
Forumaš(ica)
Pridružen/a: 19. 08. 2004. (11:29:05)
Postovi: (175)16
|
|
| [Vrh] |
|
ZELENIZUBNAPLANETIDO
SADE
Forumaš(ica)
Pridružen/a: 04. 03. 2004. (19:56:15)
Postovi: (54F)16
Lokacija: hm?
|
| Postano: 11:22 sub, 28. 8. 2004 Naslov: |
|
|
|
[quote="Vincent Van Ear"]ali to ne mijenja činjenicu da mi je floor(x) _prekidna na segmentu_,što ja tu točku prekida apsolutno zanemarujem?[/quote]
Sijeti se "Doka Leme" ([i]ako se dvije fje razlikuju....[/i]) ;)
Tj. ako ti imas fju neprekidnu na intervalu, tada ona ima svoju prim fju. Bez obzira na to kako mi dodefinirali, prekidno, ili neprekidno, tu fju u rubnim tockama, po "doka lemi", sve te fje imaju istu vrijednost integrala.
Ne moras zanemariti tu "tocku prekida", dapace ne smijes :D potpuno je druga stvar sto je ona ovdje jednostavno nebitna :g:
| Vincent Van Ear (napisa): | | ali to ne mijenja činjenicu da mi je floor(x) _prekidna na segmentu_,što ja tu točku prekida apsolutno zanemarujem? |
Sijeti se "Doka Leme" (ako se dvije fje razlikuju....)
Tj. ako ti imas fju neprekidnu na intervalu, tada ona ima svoju prim fju. Bez obzira na to kako mi dodefinirali, prekidno, ili neprekidno, tu fju u rubnim tockama, po "doka lemi", sve te fje imaju istu vrijednost integrala.
Ne moras zanemariti tu "tocku prekida", dapace ne smijes  potpuno je druga stvar sto je ona ovdje jednostavno nebitna
_________________
Pupoljak nije negiran. Rekao sam to i ponovit cu to jos jedanput. Pupoljak NIJE negirAn.
MADD
(Mothers Against Dirty Dialectics)
Based on a true story. NOT.
Ko ih sljivi, mi sviramo punk |
|
| [Vrh] |
|
Vincent Van Ear
Forumaš(ica)
Pridružen/a: 19. 08. 2004. (11:29:05)
Postovi: (175)16
|
| Postano: 11:39 sub, 28. 8. 2004 Naslov: |
|
|
|
[quote="ZELENIZUBNAPLANETIDOSADE"][quote="Vincent Van Ear"]ali to ne mijenja činjenicu da mi je floor(x) _prekidna na segmentu_,što ja tu točku prekida apsolutno zanemarujem?[/quote]
Sijeti se "Doka Leme" ([i]ako se dvije fje razlikuju....[/i]) ;)
Tj. ako ti imas fju neprekidnu na intervalu, tada ona ima svoju prim fju. Bez obzira na to kako mi dodefinirali, prekidno, ili neprekidno, tu fju u rubnim tockama, po "doka lemi", sve te fje imaju istu vrijednost integrala.
Ne moras zanemariti tu "tocku prekida", dapace ne smijes :D potpuno je druga stvar sto je ona ovdje jednostavno nebitna :g:[/quote]
Aha,imam konstantu y=1 na segmentu od 1 do 2 i ona je tu neprekidna.
Reiman kaže da je ona tu i integrabilna.
Dodefiniram tu funkciju u funkciju y1=1 tako da u točki 2 ima prekid slijeva.
Nije bitno,ona je integrabilna.
Jeli to lema,pomoćna tvrdnja,zašto je nemam u bilježnici ni profesor Kurepa u knjizi,a tvrdnja je stvarno jaka.
| ZELENIZUBNAPLANETIDOSADE (napisa): | | Vincent Van Ear (napisa): | | ali to ne mijenja činjenicu da mi je floor(x) _prekidna na segmentu_,što ja tu točku prekida apsolutno zanemarujem? |
Sijeti se "Doka Leme" (ako se dvije fje razlikuju....)
Tj. ako ti imas fju neprekidnu na intervalu, tada ona ima svoju prim fju. Bez obzira na to kako mi dodefinirali, prekidno, ili neprekidno, tu fju u rubnim tockama, po "doka lemi", sve te fje imaju istu vrijednost integrala.
Ne moras zanemariti tu "tocku prekida", dapace ne smijes potpuno je druga stvar sto je ona ovdje jednostavno nebitna |
Aha,imam konstantu y=1 na segmentu od 1 do 2 i ona je tu neprekidna.
Reiman kaže da je ona tu i integrabilna.
Dodefiniram tu funkciju u funkciju y1=1 tako da u točki 2 ima prekid slijeva.
Nije bitno,ona je integrabilna.
Jeli to lema,pomoćna tvrdnja,zašto je nemam u bilježnici ni profesor Kurepa u knjizi,a tvrdnja je stvarno jaka.
_________________
Samo sam jedan čovjek,
samo jedan pakao.
|
|
| [Vrh] |
|
mdoko
Forumaš(ica)
Pridružen/a: 30. 11. 2002. (22:17:12)
Postovi: (71A)16
Spol:
Lokacija: Heriot-Watt University, Edinburgh
|
| Postano: 11:59 sub, 28. 8. 2004 Naslov: |
|
|
|
[quote]Jeli to lema,pomoćna tvrdnja,zašto je nemam u bilježnici ni profesor Kurepa u knjizi,a tvrdnja je stvarno jaka.[/quote]
Mozda je u biljeznici nemas iz razloga jer je jednostavno nisi zapisao, a mozda stvarno nije ni izrecena. Kada sam ja bio na prvoj godini to nije bilo izreceno na prdavanjima, nego na vjezbama i ne bas u takvom obliku. Bilo je receno, da za vrijednost integrala nije bitno ako promijenimo vrijednost funkcije u jednoj tocki. Mene je takva formulacija malo zasmetala, pa sam se potrudio to formalno dokazati :cool: Nije dobro ocekivati da ti se sve servira na predavanjima i vjezbama, nego se ponekad nesto samo natukne, a nekad cak i preskoci (vjerojatno ne namjerno). Ove stvarcice koje se na predavanjima ne prezentiraju do detalja su jako korisne ako ih pokusas sam precizno formulirati i dokazati.
P.S. nemoj se pretjerano zamarati s tim da li ces neku tvrdnju nazvati teorem, propozicija, lema, korolar ili nesto slicno. To bas i nije od prsudne vaznosti.
| Citat: | | Jeli to lema,pomoćna tvrdnja,zašto je nemam u bilježnici ni profesor Kurepa u knjizi,a tvrdnja je stvarno jaka. |
Mozda je u biljeznici nemas iz razloga jer je jednostavno nisi zapisao, a mozda stvarno nije ni izrecena. Kada sam ja bio na prvoj godini to nije bilo izreceno na prdavanjima, nego na vjezbama i ne bas u takvom obliku. Bilo je receno, da za vrijednost integrala nije bitno ako promijenimo vrijednost funkcije u jednoj tocki. Mene je takva formulacija malo zasmetala, pa sam se potrudio to formalno dokazati  Nije dobro ocekivati da ti se sve servira na predavanjima i vjezbama, nego se ponekad nesto samo natukne, a nekad cak i preskoci (vjerojatno ne namjerno). Ove stvarcice koje se na predavanjima ne prezentiraju do detalja su jako korisne ako ih pokusas sam precizno formulirati i dokazati.
P.S. nemoj se pretjerano zamarati s tim da li ces neku tvrdnju nazvati teorem, propozicija, lema, korolar ili nesto slicno. To bas i nije od prsudne vaznosti.
_________________
Extraordinary claims require extraordinary evidence. – Carl Sagan
|
|
| [Vrh] |
|
Vincent Van Ear
Forumaš(ica)
Pridružen/a: 19. 08. 2004. (11:29:05)
Postovi: (175)16
|
| Postano: 13:20 sub, 28. 8. 2004 Naslov: |
|
|
|
Hvala. :wink:
A što se tiče samostalnog dokazivanja,potpuno si u pravu ali nemam baš mnogo vremena pa zato ne skrećem sa zadane putanje,pratim u bilježnici sve ono što se izdešavalo na predavanjima,a onda kasnije kada prođe bitka na usmenom onda se mogu sladiti ovakvim stvarima,sada stvarno nemam vremena.
Hvala.
A što se tiče samostalnog dokazivanja,potpuno si u pravu ali nemam baš mnogo vremena pa zato ne skrećem sa zadane putanje,pratim u bilježnici sve ono što se izdešavalo na predavanjima,a onda kasnije kada prođe bitka na usmenom onda se mogu sladiti ovakvim stvarima,sada stvarno nemam vremena.
_________________
Samo sam jedan čovjek,
samo jedan pakao.
|
|
| [Vrh] |
|
|
