| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
uvelaruza
Forumaš(ica)
Pridružen/a: 05. 03. 2013. (13:30:02)
Postovi: (E)16
|
|
| [Vrh] |
|
If and only if
Forumaš(ica)


Pridružen/a: 30. 09. 2012. (18:16:22)
Postovi: (1F)16
Spol: 
|
|
| [Vrh] |
|
Zenon
Forumaš(ica)


Pridružen/a: 09. 09. 2011. (19:14:43)
Postovi: (2B1)16
Sarma: -
Lokacija: [tex]\pm\infty[/tex]
|
 Postano: 17:07 uto, 5. 3. 2013 Naslov: Postano: 17:07 uto, 5. 3. 2013 Naslov: |
    |
|
|
[quote="If and only if"]Ja bi to ovako: [latex] \ lim_{n\to\infty} ((n^{1/n} - 1))^n=(\ lim_{n\to\infty} (n^{1/n} - 1))^n=(\ lim_{n\to\infty}(n^{1/n}) - 1)^n=(1-1)^n=0^n=0[/latex][/quote]
Iako to jest točan rezultat, postupak jednostavno nije. To bi mogao napraviti da limes glasi [dtex]\lim_{n\to\infty}(\sqrt[n]{n}-1)^x,[/dtex] gdje je [tex]x\in\mathbb R\setminus\{0\}[/tex], ali u ovom slučaju eksponent ovisi o samom [tex]n[/tex]. Ne možeš ti "parcijalno pustiti limes".
Očiti kontrapimjer bio bi [dtex]\lim_n (n^{1/n})^n=(\lim_n n^{1/n})^n=1^n=1,[/dtex] dok, s druge strane, [dtex]\lim_n (n^{1/n})^n=\lim_n n^{\frac nn}=\lim_n n=+\infty .[/dtex]
[size=9][color=#999999]Added after 21 minutes:[/color][/size]
Ja bih to nekako ovako. Neka je [tex]\varepsilon >0[/tex] proizvoljan. S obzirom da znamo da [tex]\sqrt[n]{n}\to 1,[/tex] vrijedi [dtex](\forall \varepsilon ' >0)(\exists n_{\varepsilon '}\in\mathbb N) n\geq n_{\varepsilon '} \implies \vert \sqrt[n]{n}-1\vert <\varepsilon ' .[/dtex] Dakle, postoji [tex]n_0[/tex] takav da za svaki [tex]n\geq n_0[/tex] vrijedi [dtex]0\leq\sqrt[n]{n}-1=\vert \sqrt[n]{n}-1\vert<\frac 12\Longleftrightarrow (\sqrt[n]{n}-1)^n<\left(\frac 12\right)^n.[/dtex] S obzirom da znamo da [tex](\frac 12)^n\to 0[/tex], slijedi da postoji [tex]n_1[/tex] takav da [dtex]n\geq n_1\implies \left(\frac 12\right)^n <\varepsilon .[/dtex] Uzmimo sada [tex]n_{\varepsilon}=\text{max}\{n_0, n_1\}[/tex] i za [tex]n\geq n_{\varepsilon}[/tex] vrijedi [dtex]\vert (\sqrt[n]{n}-1)^n-0\vert =(\sqrt[n]{n}-1)^n<\left(\frac 12\right)^n<\varepsilon .[/dtex] Dakle, po definiciji smo pokazali da je limes jednak 0.
| If and only if (napisa): | Ja bi to ovako: 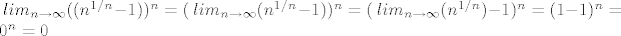 |
Iako to jest točan rezultat, postupak jednostavno nije. To bi mogao napraviti da limes glasi [dtex]\lim_{n\to\infty}(\sqrt[n]{n}-1)^x,[/dtex] gdje je [tex]x\in\mathbb R\setminus\{0\}[/tex], ali u ovom slučaju eksponent ovisi o samom [tex]n[/tex]. Ne možeš ti "parcijalno pustiti limes".
Očiti kontrapimjer bio bi [dtex]\lim_n (n^{1/n})^n=(\lim_n n^{1/n})^n=1^n=1,[/dtex] dok, s druge strane, [dtex]\lim_n (n^{1/n})^n=\lim_n n^{\frac nn}=\lim_n n=+\infty .[/dtex]
Added after 21 minutes:
Ja bih to nekako ovako. Neka je [tex]\varepsilon >0[/tex] proizvoljan. S obzirom da znamo da [tex]\sqrt[n]{n}\to 1,[/tex] vrijedi [dtex](\forall \varepsilon ' >0)(\exists n_{\varepsilon '}\in\mathbb N) n\geq n_{\varepsilon '} \implies \vert \sqrt[n]{n}-1\vert <\varepsilon ' .[/dtex] Dakle, postoji [tex]n_0[/tex] takav da za svaki [tex]n\geq n_0[/tex] vrijedi [dtex]0\leq\sqrt[n]{n}-1=\vert \sqrt[n]{n}-1\vert<\frac 12\Longleftrightarrow (\sqrt[n]{n}-1)^n<\left(\frac 12\right)^n.[/dtex] S obzirom da znamo da [tex](\frac 12)^n\to 0[/tex], slijedi da postoji [tex]n_1[/tex] takav da [dtex]n\geq n_1\implies \left(\frac 12\right)^n <\varepsilon .[/dtex] Uzmimo sada [tex]n_{\varepsilon}=\text{max}\{n_0, n_1\}[/tex] i za [tex]n\geq n_{\varepsilon}[/tex] vrijedi [dtex]\vert (\sqrt[n]{n}-1)^n-0\vert =(\sqrt[n]{n}-1)^n<\left(\frac 12\right)^n<\varepsilon .[/dtex] Dakle, po definiciji smo pokazali da je limes jednak 0.
|
|
| [Vrh] |
|
If and only if
Forumaš(ica)


Pridružen/a: 30. 09. 2012. (18:16:22)
Postovi: (1F)16
Spol: 
|
|
| [Vrh] |
|
satja
Forumaš(ica)

Pridružen/a: 16. 05. 2010. (10:44:17)
Postovi: (F1)16
|
|
| [Vrh] |
|
If and only if
Forumaš(ica)


Pridružen/a: 30. 09. 2012. (18:16:22)
Postovi: (1F)16
Spol: 
|
|
| [Vrh] |
|
uvelaruza
Forumaš(ica)
Pridružen/a: 05. 03. 2013. (13:30:02)
Postovi: (E)16
|
|
| [Vrh] |
|
Zenon
Forumaš(ica)


Pridružen/a: 09. 09. 2011. (19:14:43)
Postovi: (2B1)16
Sarma: -
Lokacija: [tex]\pm\infty[/tex]
|
 Postano: 23:43 uto, 5. 3. 2013 Naslov: Postano: 23:43 uto, 5. 3. 2013 Naslov: |
    |
|
|
Neovisno o tome što za nizove vrijedi ili ne vrijedi, ono rješenje (tj. onaj zapis rješenja) jednostavno je krivo i neispravno.
Nadalje, da mi nismo reagirali, to krivo rješenje bi stajalno na forumu bez dodatnih opravdanja i argumentacije i ovisno o razumjevanju osobe koja je tražila rješenje, ili bi "otišla kući" s krivim rješenjem, ili čekala da netko da ispravan odgovor.
S obzirom na sve te daljnje argumente, ako si ih apriori znao, ne vidim zašto si uopće pisao onaj neispravan račun, a ne odmah pokazao puno općenitiji rezultat ili, kao satja, napisao koji si oblik teorema o sendviču imao u glavi (to svakako zahtjeva manje tipkanja u tex-u)?
No dobro, kako ova tema ne bi prerasla u raspravu nevezanu uz sami zadatak, ovdje stajem s postovima (a pogotovo jer mi se čini da se ponavlja [url=http://degiorgi.math.hr/forum/viewtopic.php?p=179422#179422]ovo[/url] popračeno [url=http://degiorgi.math.hr/forum/viewtopic.php?p=179426#179426]ovim[/url], zaključno s [url=http://degiorgi.math.hr/forum/viewtopic.php?p=179437#179437]ovim[/url]).
Neovisno o tome što za nizove vrijedi ili ne vrijedi, ono rješenje (tj. onaj zapis rješenja) jednostavno je krivo i neispravno.
Nadalje, da mi nismo reagirali, to krivo rješenje bi stajalno na forumu bez dodatnih opravdanja i argumentacije i ovisno o razumjevanju osobe koja je tražila rješenje, ili bi "otišla kući" s krivim rješenjem, ili čekala da netko da ispravan odgovor.
S obzirom na sve te daljnje argumente, ako si ih apriori znao, ne vidim zašto si uopće pisao onaj neispravan račun, a ne odmah pokazao puno općenitiji rezultat ili, kao satja, napisao koji si oblik teorema o sendviču imao u glavi (to svakako zahtjeva manje tipkanja u tex-u)?
No dobro, kako ova tema ne bi prerasla u raspravu nevezanu uz sami zadatak, ovdje stajem s postovima (a pogotovo jer mi se čini da se ponavlja ovo popračeno ovim, zaključno s ovim).
|
|
| [Vrh] |
|
tiborr
Forumaš(ica)
Pridružen/a: 23. 12. 2012. (18:54:28)
Postovi: (E)16
|
|
| [Vrh] |
|
matkec
Forumaš(ica)


Pridružen/a: 14. 05. 2010. (16:21:29)
Postovi: (8C)16
|
|
| [Vrh] |
|
Nightrider
Forumaš s poteškoćama u pisanju


Pridružen/a: 19. 03. 2013. (19:01:05)
Postovi: (61)16
Spol: 
|
|
| [Vrh] |
|
matkec
Forumaš(ica)


Pridružen/a: 14. 05. 2010. (16:21:29)
Postovi: (8C)16
|
|
| [Vrh] |
|
Nightrider
Forumaš s poteškoćama u pisanju


Pridružen/a: 19. 03. 2013. (19:01:05)
Postovi: (61)16
Spol: 
|
 Postano: 11:26 pet, 22. 3. 2013 Naslov: Postano: 11:26 pet, 22. 3. 2013 Naslov: |
    |
|
|
[quote="matkec"][quote="Nightrider"]A ja sam zapeo na ovome, molim vas ne pitajte kako sam dosao do ovoga:
Postoji li limes:
[latex]\lim_ {x\to \infty}\dfrac {cos^5xsin^5x} {x^8sin^2x-2x^7sinxcos^2x+x^6cos^4x+x^2cos^8x}[/latex]
Ima li neki strucnjak za limese ili je ovo nesto trivijalno samo ja ne vidim nacin?[/quote]
Cijenio bih da staviš originalni zadatak. Ovo mi se čini da si zakomplicirao neki zadatak, pa se ne vidi lako koje je rješenje, no možda je tom zadatku trebalo drugačije pristupiti.[/quote]
Evo, ako ti imalo pomaze, pa ti rjesavaj kako god ti srce zeli:
[latex]\lim_ {x\to \infty}\dfrac {{(cosxsinx)^5\over x^{10}}}{({sinx\over x}-{cos^2x\over x^2})^2+{cos^8x\over x^8}}[/latex]
| matkec (napisa): | | Nightrider (napisa): | A ja sam zapeo na ovome, molim vas ne pitajte kako sam dosao do ovoga:
Postoji li limes:
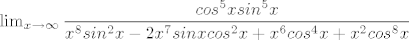
Ima li neki strucnjak za limese ili je ovo nesto trivijalno samo ja ne vidim nacin? |
Cijenio bih da staviš originalni zadatak. Ovo mi se čini da si zakomplicirao neki zadatak, pa se ne vidi lako koje je rješenje, no možda je tom zadatku trebalo drugačije pristupiti. |
Evo, ako ti imalo pomaze, pa ti rjesavaj kako god ti srce zeli:
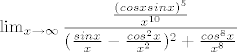
|
|
| [Vrh] |
|
matkec
Forumaš(ica)


Pridružen/a: 14. 05. 2010. (16:21:29)
Postovi: (8C)16
|
 Postano: 21:20 pet, 22. 3. 2013 Naslov: Postano: 21:20 pet, 22. 3. 2013 Naslov: |
    |
|
|
[quote="Nightrider"]
[latex]\lim_ {x\to \infty}\dfrac {{(cosxsinx)^5\over x^{10}}}{({sinx\over x}-{cos^2x\over x^2})^2+{cos^8x\over x^8}}[/latex][/quote]
Uf, ne znam odakle ti ovaj zadatak, izgleda odvratno.
Nisam baš puno razmišljao, više sam sam se uzdao u Wolframa. Prvo ne želi izračunat limes, no kad se nacrta graf, izgleda da je nula...
Pokušat ću još malo, treba biti neka finta s ograničavanjem sinusa i cosinusa ( <=1 ), pa da onda polinom nadvlada.
(Dan poslije...)
Evo ga:
Kao što sam i najavio, sve trigonometrijske funkcije ćemo nekako ograničiti i pustiti polinomima da odrade svoje. Umjesto da gledamo originalni limes, gledat ćemo limes apsolutne vrijednosti cijelog izraza i dokazati da je on jednak nuli.
Brojnik je lagano ograničiti: [tex] | (cosxsinx)^5 | \leq 1 [/tex]. Nazivnik će biti puno teže, jer ga moramo ograničiti odozdo.
Dokazat ćemo sljedeću tvrdnju: [tex] x^4(x sinx - cos^2x)^2 + cos^8x \geq \frac{1}{16} [/tex], za sve [tex] x >2[/tex]. (Odabrane konstante su mogle biti i drukčije).
Pretpostavimo suprotno, tj. [tex] x^4(x sinx - cos^2x)^2 + cos^8x < \frac{1}{16} [/tex], za neki [tex]x>2[/tex]. Kako je izraz slijeva zbroj dva nenegativna broja, da bi vrijedila nejednakost nužno moraju vrijediti i sljedeće dvije nejednakosti:
a) [tex] cos^8x < \frac{1}{16}[/tex] => [tex] cos^2 x < \frac{1}{2} (1) [/tex]
b) [tex] x^4 (xsinx - cos^2x)^2 < \frac{1}{16}[/tex]
=> [tex] |xsinx - cos^2 x | < \frac{1}{16} [/tex] (iskoristli smo x>2)
=> [tex]- \frac{1}{16} < xsinx - cos^2x < \frac{1}{16}[/tex]
=> [tex] - \frac{1}{16} -1 <xsinx < \frac{1}{16} +1 [/tex] (iskoristili smo [tex]-1 < 0 \leq cos^2x \leq 1 [/tex])
=> [tex] |sin x| < \frac{17}{32} < \frac{2}{3} (2) [/tex]
Iz novodobivenih nejednakosti (1) i (2) dobivamo da za taj neki [tex]x>2[/tex] vrijedi [tex]1 = sin^2x+cos^2x < \frac{4}{9} + \frac{1}{2} = \frac{17}{18}[/tex], što nije istina. Kontradikcija.
Sada možemo usendvičiti naš limes:
[latex] 0 \leq \lvert \dfrac {{(cosxsinx)^5\over x^{10}}}{({sinx\over x}-{cos^2x\over x^2})^2+{cos^8x\over x^8}} \rvert = \lvert \dfrac {{(cosxsinx)^5\over x^{10}}}{ \frac{x^4(x sinx - cos^2x)^2 + cos^8x}{x^8}} \rvert \leq \frac{\frac{1}{x^{10}}}{\frac{1}{16 x^8}} = \frac{16}{x^2} [/latex]
Sad je jasno da i lijeva i desna strana idu u nulu kada x ide u plus beskonačno.
| Nightrider (napisa): |
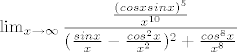 |
Uf, ne znam odakle ti ovaj zadatak, izgleda odvratno.
Nisam baš puno razmišljao, više sam sam se uzdao u Wolframa. Prvo ne želi izračunat limes, no kad se nacrta graf, izgleda da je nula...
Pokušat ću još malo, treba biti neka finta s ograničavanjem sinusa i cosinusa ( ⇐1 ), pa da onda polinom nadvlada.
(Dan poslije...)
Evo ga:
Kao što sam i najavio, sve trigonometrijske funkcije ćemo nekako ograničiti i pustiti polinomima da odrade svoje. Umjesto da gledamo originalni limes, gledat ćemo limes apsolutne vrijednosti cijelog izraza i dokazati da je on jednak nuli.
Brojnik je lagano ograničiti: [tex] | (cosxsinx)^5 | \leq 1 [/tex]. Nazivnik će biti puno teže, jer ga moramo ograničiti odozdo.
Dokazat ćemo sljedeću tvrdnju: [tex] x^4(x sinx - cos^2x)^2 + cos^8x \geq \frac{1}{16} [/tex], za sve [tex] x >2[/tex]. (Odabrane konstante su mogle biti i drukčije).
Pretpostavimo suprotno, tj. [tex] x^4(x sinx - cos^2x)^2 + cos^8x < \frac{1}{16} [/tex], za neki [tex]x>2[/tex]. Kako je izraz slijeva zbroj dva nenegativna broja, da bi vrijedila nejednakost nužno moraju vrijediti i sljedeće dvije nejednakosti:
a) [tex] cos^8x < \frac{1}{16}[/tex] ⇒ [tex] cos^2 x < \frac{1}{2} (1) [/tex]
b) [tex] x^4 (xsinx - cos^2x)^2 < \frac{1}{16}[/tex]
⇒ [tex] |xsinx - cos^2 x | < \frac{1}{16} [/tex] (iskoristli smo x>2)
⇒ [tex]- \frac{1}{16} < xsinx - cos^2x < \frac{1}{16}[/tex]
⇒ [tex] - \frac{1}{16} -1 <xsinx < \frac{1}{16} +1 [/tex] (iskoristili smo [tex]-1 < 0 \leq cos^2x \leq 1 [/tex])
⇒ [tex] |sin x| < \frac{17}{32} < \frac{2}{3} (2) [/tex]
Iz novodobivenih nejednakosti (1) i (2) dobivamo da za taj neki [tex]x>2[/tex] vrijedi [tex]1 = sin^2x+cos^2x < \frac{4}{9} + \frac{1}{2} = \frac{17}{18}[/tex], što nije istina. Kontradikcija.
Sada možemo usendvičiti naš limes:
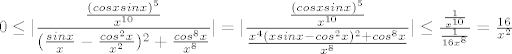
Sad je jasno da i lijeva i desna strana idu u nulu kada x ide u plus beskonačno.
|
|
| [Vrh] |
|
Nightrider
Forumaš s poteškoćama u pisanju


Pridružen/a: 19. 03. 2013. (19:01:05)
Postovi: (61)16
Spol: 
|
|
| [Vrh] |
|
pllook
Forumaš(ica)

Pridružen/a: 08. 11. 2013. (20:56:12)
Postovi: (CD)16
Spol: 
|
|
| [Vrh] |
|
vsego
Site Admin


Pridružen/a: 06. 10. 2002. (22:07:09)
Postovi: (3562)16
Spol: 
Lokacija: /sbin/init
|
|
| [Vrh] |
|
pllook
Forumaš(ica)

Pridružen/a: 08. 11. 2013. (20:56:12)
Postovi: (CD)16
Spol: 
|
|
| [Vrh] |
|
|













