| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
fkirsek
Forumaš(ica)
Pridružen/a: 28. 09. 2012. (23:52:51)
Postovi: (23)16
|
 Postano: 19:44 čet, 21. 3. 2013 Naslov: |
    |
|
|
Da, samo trebaš to integrirati i to je srednja vrijednost.
4. zadatak:
Skiciraš si kvadrat i te subdivizije. [tex]x+y[/tex] raste i po x-u i po y-onu, pa će maksimum i minimum u svakom dijelu subdivizije biti postignuti u donjem lijevom, tj. gornjem desnom kutu tog dijela subdivizije. Površine tih pravokutnika također lako isčitaš. Donja Darbouxova suma je upravo zbroj svih površina pomnoženih sa minimumima na tom dijelu, gornja isto, ali sa maksimumima. Dakle
[tex]
s(P) = 0*2 + 1*2 + 2*1 + 3*1 = 7
S(P) = 3*2 + 4*2 + 4*1 + 5*1 = 23
[/tex]
Za c), neku drugu integralnu sumu možeš dobiti tako da umeš primjerice vrijednosti u sredini svakog pravokutnika.
Za d) je odgovor DA, to nam garantira teorem srednje vrijednosti. Naime, na svakom tom pravokutniku ga možemo iskoristiti posebno i onda odabrati upravo te točke da dobijemo cijeli integral.
6. zad ću još pogledati.
[size=9][color=#999999]Added after 13 minutes:[/color][/size]
Za 6. zadatak, sva tri odgovora su DA
a) slijedi iz b), a b) ti je upravo primjer 6.4. u skripti.
c) je također odgovor DA jer je to upravo razlog računanja integrala sa Analize :D (a i zato što je skup prekida tog skupa opet površine nula)
Da, samo trebaš to integrirati i to je srednja vrijednost.
4. zadatak:
Skiciraš si kvadrat i te subdivizije. [tex]x+y[/tex] raste i po x-u i po y-onu, pa će maksimum i minimum u svakom dijelu subdivizije biti postignuti u donjem lijevom, tj. gornjem desnom kutu tog dijela subdivizije. Površine tih pravokutnika također lako isčitaš. Donja Darbouxova suma je upravo zbroj svih površina pomnoženih sa minimumima na tom dijelu, gornja isto, ali sa maksimumima. Dakle
[tex]
s(P) = 0*2 + 1*2 + 2*1 + 3*1 = 7
S(P) = 3*2 + 4*2 + 4*1 + 5*1 = 23
[/tex]
Za c), neku drugu integralnu sumu možeš dobiti tako da umeš primjerice vrijednosti u sredini svakog pravokutnika.
Za d) je odgovor DA, to nam garantira teorem srednje vrijednosti. Naime, na svakom tom pravokutniku ga možemo iskoristiti posebno i onda odabrati upravo te točke da dobijemo cijeli integral.
6. zad ću još pogledati.
Added after 13 minutes:
Za 6. zadatak, sva tri odgovora su DA
a) slijedi iz b), a b) ti je upravo primjer 6.4. u skripti.
c) je također odgovor DA jer je to upravo razlog računanja integrala sa Analize  (a i zato što je skup prekida tog skupa opet površine nula)
|
|
| [Vrh] |
|
pedro
Forumaš(ica)
Pridružen/a: 21. 10. 2010. (14:08:21)
Postovi: (19B)16
|
| Postano: 15:25 sub, 23. 3. 2013 Naslov: |
|
|
|
[quote="fkirsek"]
4. zadatak od iste godine:
Dakle, pitanje je ima li skup [tex]L(C )[/tex] površinu. Koristit ćemo teorem o zamjeni varijabli (iako možemo koristiti i Korolar 9.5 koji će isti rezultat dati izravno). Prvo, primjetimo da je L regularna matrica, tj. da će determinanta preslikavanja L(x,y) biti različita od nule. Prema teoremu o zamjeni varijabli (ili Korolaru 9.5) dobijamo da, ako [tex]C[/tex] ima površinu, onda i [tex]L(C)[/tex] ima površinu i ta površina je upravo [tex] |det L|\nu(C) [/tex].
Štoviše, pošto je [tex]L[/tex] regularan, postoji inverzno preslikavanje [tex]L^{-1}[/tex], pa vrijedi i obrnuto, ako skup [tex]L(C)[/tex] ima površinu, onda ju ima i skup [tex]C[/tex]. Obratom po kontrapoziciji dobijemo: ako skup [tex]C[/tex] nema površinu, nema je ni skup [tex]L(C)[/tex].
Ukratko, vrijedi:
[tex]L(C)[/tex] ima površinu ako i samo ako skup [tex]C[/tex] ima površinu.
Dakle, trebamo to provjeriti samo za skup [tex]C[/tex]. Skup [tex]C[/tex]. će imati površinu ako je ograničen i ako mu je rub skup mjere nula.
Je li skup [tex]C[/tex] ograničen? Da! Lako se pokaže (vidi sa grafa, ako ništa drugo) da je taj skup sadržan u pravokutniku čiji su rubovi točke [tex](0,0), (0,3), (1,0), (1,3)[/tex], dakle ograničen je.
Je li rub skupa mjere nula?
Također je jasno da je rub skupa unija tri dužine (koje su mjere nula) i grafa funkcije [tex]f(x) = \frac{1}{1+x}[/tex] na segmentu [tex][0,3][/tex].
Znamo da vrijedi da je graf neprekidne funkcije na segmentu mjere nula. Gornja funkcija je zaista takva pa je njen graf mjere nula. Dakle rub skupa [tex]C[/tex] je konačna unija skupova mjere nula, pa je i sam mjere nula.
Dakle [tex]C[/tex] ima površinu, pa površinu ima i [tex]L(C)[/tex].
[/quote]
je li površina od L(C) = ln4 - ln1?
| fkirsek (napisa): |
4. zadatak od iste godine:
Dakle, pitanje je ima li skup [tex]L(C )[/tex] površinu. Koristit ćemo teorem o zamjeni varijabli (iako možemo koristiti i Korolar 9.5 koji će isti rezultat dati izravno). Prvo, primjetimo da je L regularna matrica, tj. da će determinanta preslikavanja L(x,y) biti različita od nule. Prema teoremu o zamjeni varijabli (ili Korolaru 9.5) dobijamo da, ako [tex]C[/tex] ima površinu, onda i [tex]L(C)[/tex] ima površinu i ta površina je upravo [tex] |det L|\nu(C) [/tex].
Štoviše, pošto je [tex]L[/tex] regularan, postoji inverzno preslikavanje [tex]L^{-1}[/tex], pa vrijedi i obrnuto, ako skup [tex]L(C)[/tex] ima površinu, onda ju ima i skup [tex]C[/tex]. Obratom po kontrapoziciji dobijemo: ako skup [tex]C[/tex] nema površinu, nema je ni skup [tex]L(C)[/tex].
Ukratko, vrijedi:
[tex]L(C)[/tex] ima površinu ako i samo ako skup [tex]C[/tex] ima površinu.
Dakle, trebamo to provjeriti samo za skup [tex]C[/tex]. Skup [tex]C[/tex]. će imati površinu ako je ograničen i ako mu je rub skup mjere nula.
Je li skup [tex]C[/tex] ograničen? Da! Lako se pokaže (vidi sa grafa, ako ništa drugo) da je taj skup sadržan u pravokutniku čiji su rubovi točke [tex](0,0), (0,3), (1,0), (1,3)[/tex], dakle ograničen je.
Je li rub skupa mjere nula?
Također je jasno da je rub skupa unija tri dužine (koje su mjere nula) i grafa funkcije [tex]f(x) = \frac{1}{1+x}[/tex] na segmentu [tex][0,3][/tex].
Znamo da vrijedi da je graf neprekidne funkcije na segmentu mjere nula. Gornja funkcija je zaista takva pa je njen graf mjere nula. Dakle rub skupa [tex]C[/tex] je konačna unija skupova mjere nula, pa je i sam mjere nula.
Dakle [tex]C[/tex] ima površinu, pa površinu ima i [tex]L(C)[/tex].
|
je li površina od L(C) = ln4 - ln1?
|
|
| [Vrh] |
|
fkirsek
Forumaš(ica)
Pridružen/a: 28. 09. 2012. (23:52:51)
Postovi: (23)16
|
| Postano: 16:28 sub, 23. 3. 2013 Naslov: |
|
|
|
[quote="pedro"]je li površina od L(C) = ln4 - ln1?[/quote]
Da, pošto je determinanta preslikavanja 1, površina od L(C) je isto što i površina od C, a to je pak integral ispod te krivulje što je, kao što si rekla, [tex]ln 4[/tex] ( jer je [tex]ln 1=0[/tex])
| pedro (napisa): | | je li površina od L(C) = ln4 - ln1? |
Da, pošto je determinanta preslikavanja 1, površina od L(C) je isto što i površina od C, a to je pak integral ispod te krivulje što je, kao što si rekla, [tex]ln 4[/tex] ( jer je [tex]ln 1=0[/tex])
|
|
| [Vrh] |
|
pedro
Forumaš(ica)
Pridružen/a: 21. 10. 2010. (14:08:21)
Postovi: (19B)16
|
| Postano: 12:57 ned, 24. 3. 2013 Naslov: |
|
|
|
[quote="fkirsek"]Da, samo trebaš to integrirati i to je srednja vrijednost.
4. zadatak:
Skiciraš si kvadrat i te subdivizije. [tex]x+y[/tex] raste i po x-u i po y-onu, pa će maksimum i minimum u svakom dijelu subdivizije biti postignuti u donjem lijevom, tj. gornjem desnom kutu tog dijela subdivizije. Površine tih pravokutnika također lako isčitaš. Donja Darbouxova suma je upravo zbroj svih površina pomnoženih sa minimumima na tom dijelu, gornja isto, ali sa maksimumima. Dakle
[tex]
s(P) = 0*2 + 1*2 + 2*1 + 3*1 = 7
S(P) = 3*2 + 4*2 + 4*1 + 5*1 = 23
[/tex]
[/quote]
nacrtala sam si i nikak ne mogu skužiti ovo za min i max koje točke uzimam
| fkirsek (napisa): | Da, samo trebaš to integrirati i to je srednja vrijednost.
4. zadatak:
Skiciraš si kvadrat i te subdivizije. [tex]x+y[/tex] raste i po x-u i po y-onu, pa će maksimum i minimum u svakom dijelu subdivizije biti postignuti u donjem lijevom, tj. gornjem desnom kutu tog dijela subdivizije. Površine tih pravokutnika također lako isčitaš. Donja Darbouxova suma je upravo zbroj svih površina pomnoženih sa minimumima na tom dijelu, gornja isto, ali sa maksimumima. Dakle
[tex]
s(P) = 0*2 + 1*2 + 2*1 + 3*1 = 7
S(P) = 3*2 + 4*2 + 4*1 + 5*1 = 23
[/tex]
|
nacrtala sam si i nikak ne mogu skužiti ovo za min i max koje točke uzimam
|
|
| [Vrh] |
|
fkirsek
Forumaš(ica)
Pridružen/a: 28. 09. 2012. (23:52:51)
Postovi: (23)16
|
|
| [Vrh] |
|
pedro
Forumaš(ica)
Pridružen/a: 21. 10. 2010. (14:08:21)
Postovi: (19B)16
|
|
| [Vrh] |
|
pedro
Forumaš(ica)
Pridružen/a: 21. 10. 2010. (14:08:21)
Postovi: (19B)16
|
|
| [Vrh] |
|
matijaB
Forumaš(ica)
Pridružen/a: 19. 08. 2010. (09:11:43)
Postovi: (4D)16
|
|
| [Vrh] |
|
Nightrider
Forumaš s poteškoćama u pisanju
Pridružen/a: 19. 03. 2013. (19:01:05)
Postovi: (61)16
Spol: 
|
| Postano: 16:43 uto, 2. 4. 2013 Naslov: |
|
|
|
[quote="matijaB"]da li kruznica ima povrsinu nula?[/quote]
Ima. Pokusaj dokazat da za svaki epsilon>0 postoji skup pravokutnika koji u potpunosti pokrivaju kruznicu i njihova je ukupna povrsina manja od epsilon (mislim da smijes uzet i neke druge kompaktne skupove osim pravokutnika).
[quote="matijaB"]cini mi se da je to ista stvar kao i duzina..samo spojeni krajevi :D pa nebi trebalo biti razlicito..ali neznam argumentirati...tnx unaprijed[/quote]
Tu si blizu pojma homeomorfizam(obostrano neprekidna bijekcija), mozes i tako(vjerojatno bi trebao izbacit jednu tocku sa kruznice no jedna tocka ne mijenja mjeru(povrsinu)) i neznam jeste li spominjali homeomorfizme uopce?
Ne znam koji su ti teoremi dostupni, mozes na dosta nacina, vjerojatno ce netko tko pozna koji se teoremi rade u kolegiju naci laksi pristup problemu. :)
(pretpostavljam i da vrijedi da ako je neki skup u [latex]\mathbb R^2[/latex] otvoren da rub tog skupa ima povrsinu nula, pa mozes i tako ako to vrijedi)
| matijaB (napisa): | | da li kruznica ima povrsinu nula? |
Ima. Pokusaj dokazat da za svaki epsilon>0 postoji skup pravokutnika koji u potpunosti pokrivaju kruznicu i njihova je ukupna povrsina manja od epsilon (mislim da smijes uzet i neke druge kompaktne skupove osim pravokutnika).
| matijaB (napisa): | | cini mi se da je to ista stvar kao i duzina..samo spojeni krajevi pa nebi trebalo biti razlicito..ali neznam argumentirati...tnx unaprijed |
Tu si blizu pojma homeomorfizam(obostrano neprekidna bijekcija), mozes i tako(vjerojatno bi trebao izbacit jednu tocku sa kruznice no jedna tocka ne mijenja mjeru(povrsinu)) i neznam jeste li spominjali homeomorfizme uopce?
Ne znam koji su ti teoremi dostupni, mozes na dosta nacina, vjerojatno ce netko tko pozna koji se teoremi rade u kolegiju naci laksi pristup problemu. 
(pretpostavljam i da vrijedi da ako je neki skup u 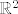 otvoren da rub tog skupa ima povrsinu nula, pa mozes i tako ako to vrijedi)
Zadnja promjena: Nightrider; 12:16 sri, 3. 4. 2013; ukupno mijenjano 1 put.
|
|
| [Vrh] |
|
mata
Forumaš(ica)
Pridružen/a: 02. 04. 2011. (17:50:57)
Postovi: (17)16
|
|
| [Vrh] |
|
fkirsek
Forumaš(ica)
Pridružen/a: 28. 09. 2012. (23:52:51)
Postovi: (23)16
|
| Postano: 17:48 sub, 6. 4. 2013 Naslov: |
|
|
|
[quote="pedro"][quote="fkirsek"][quote="pedro"]nacrtala sam si i nikak ne mogu skužiti ovo za min i max koje točke uzimam[/quote]
Pogledaj npr.jedinični kvadrat [tex][0,1]\times[0,1][/tex].
Gdje je tamo maksimum od [tex]x+y[/tex], a gdje minimum?[/quote]
joj ja sam crtala u R^2 pa mi nikak nije bilo jasno
sada je
ali možeš li pls c i d malo detaljnije objasniti
hvalaa![/quote]
Ispričavam se što duže nisam odgovarao, ipak i vaši demosi imaju kolokvije :D
Nego,
http://web.math.pmf.unizg.hr/nastava/difraf/int/2009-10/kolokvij1.pdf
4. zadatak
c) Neku drugu integralnu sumu dobiješ tako da jednostavno za svaki pravokutnik te subdivizije NE uzmeš minimum i maksimum na tom pravokutniku nego jednostavno neku drugu vrijednost.
d) Dakle, teorem srednje vrijednosti vam kaže da će za neprekidnu funkciju [tex]f[/tex] i njen integral po području [tex]A[/tex] postojati točka [tex]c[/tex] tako da je
[tex] f(c)\cdot\nu(A) = \int_A f(x) dx [/tex], gdje je [tex]\nu(A) [/tex] površina skupa [tex]A[/tex].
Sad, na prvi pogled, ne čini se da to tu koristi, jel tako? Ako to primjenimo za naš kvadrat, on će nam samo dati c za cijelo naše područje, dakle za [tex][0,2]x[0,3][/tex]. Međutim, možemo primjeniti taj teorem na svako podpodručje subdivizije posebno, dobijajću [tex]c_1, c_2,c_3, c_4[/tex] za koje vrijedi, po svakom od tih kvadrata, da je [tex]f(c_i)\cdot povrsina = \int_{pravokutnik} f(x) dx[/tex].
Kad bi zbrojili sve gornje jednadžbe, s desne strane bi dobili integral po cijelom pravokutniku [tex][0,2]x[0,3][/tex], a s lijeve integralnu sumu za taj integral.
Iako, to smo mogli i direktno. Ako se ne varam, [tex]c_i[/tex] iz gornjeg teorema će upravo biti sredine svakog od pravokutnika.
[size=9][color=#999999]Added after 32 minutes:[/color][/size]
[quote="pedro"]http://web.math.pmf.unizg.hr/nastava/difraf/int/2007-08/IFVVkol1.pdf
[/quote]
3.b)
Skoro. Ovo što si ti napisala za taj zadatak je integral po "unutrašnjosti" tog paraboloida, zapravo se traži volumen svega u cilindru OSIM tog dijela. No, pošto je volumen cilindra lako izračunati, iznosi [tex]a^3\pi[/tex], rješenje je [tex]a^3\pi - I[/tex], gdje je I integral koji si napisala.
2.
Prvi integral je dobar, u drugom x sigurno ne ide od 1 do 9 već od 1 do 3, dok su ti granice y-ona... čudne. Ne možeš imati y kao varijablu u granicama od y-on. Dakle, drugi integral bi trebao ići:
[tex]\int_0^3 \int_{x^2}^{4x+3} (x-y) dy dx[/tex]
[tex]x^2[/tex] je donja granica jer je parabola ispod pravca u tom komadiću, gledajući po y-osi.
| pedro (napisa): | | fkirsek (napisa): | | pedro (napisa): | | nacrtala sam si i nikak ne mogu skužiti ovo za min i max koje točke uzimam |
Pogledaj npr.jedinični kvadrat [tex][0,1]\times[0,1][/tex].
Gdje je tamo maksimum od [tex]x+y[/tex], a gdje minimum? |
joj ja sam crtala u R^2 pa mi nikak nije bilo jasno
sada je
ali možeš li pls c i d malo detaljnije objasniti
hvalaa! |
Ispričavam se što duže nisam odgovarao, ipak i vaši demosi imaju kolokvije
Nego,
http://web.math.pmf.unizg.hr/nastava/difraf/int/2009-10/kolokvij1.pdf
4. zadatak
c) Neku drugu integralnu sumu dobiješ tako da jednostavno za svaki pravokutnik te subdivizije NE uzmeš minimum i maksimum na tom pravokutniku nego jednostavno neku drugu vrijednost.
d) Dakle, teorem srednje vrijednosti vam kaže da će za neprekidnu funkciju [tex]f[/tex] i njen integral po području [tex]A[/tex] postojati točka [tex]c[/tex] tako da je
[tex] f(c)\cdot\nu(A) = \int_A f(x) dx [/tex], gdje je [tex]\nu(A) [/tex] površina skupa [tex]A[/tex].
Sad, na prvi pogled, ne čini se da to tu koristi, jel tako? Ako to primjenimo za naš kvadrat, on će nam samo dati c za cijelo naše područje, dakle za [tex][0,2]x[0,3][/tex]. Međutim, možemo primjeniti taj teorem na svako podpodručje subdivizije posebno, dobijajću [tex]c_1, c_2,c_3, c_4[/tex] za koje vrijedi, po svakom od tih kvadrata, da je [tex]f(c_i)\cdot povrsina = \int_{pravokutnik} f(x) dx[/tex].
Kad bi zbrojili sve gornje jednadžbe, s desne strane bi dobili integral po cijelom pravokutniku [tex][0,2]x[0,3][/tex], a s lijeve integralnu sumu za taj integral.
Iako, to smo mogli i direktno. Ako se ne varam, [tex]c_i[/tex] iz gornjeg teorema će upravo biti sredine svakog od pravokutnika.
Added after 32 minutes:
| pedro (napisa): | http://web.math.pmf.unizg.hr/nastava/difraf/int/2007-08/IFVVkol1.pdf
|
3.b)
Skoro. Ovo što si ti napisala za taj zadatak je integral po "unutrašnjosti" tog paraboloida, zapravo se traži volumen svega u cilindru OSIM tog dijela. No, pošto je volumen cilindra lako izračunati, iznosi [tex]a^3\pi[/tex], rješenje je [tex]a^3\pi - I[/tex], gdje je I integral koji si napisala.
2.
Prvi integral je dobar, u drugom x sigurno ne ide od 1 do 9 već od 1 do 3, dok su ti granice y-ona... čudne. Ne možeš imati y kao varijablu u granicama od y-on. Dakle, drugi integral bi trebao ići:
[tex]\int_0^3 \int_{x^2}^{4x+3} (x-y) dy dx[/tex]
[tex]x^2[/tex] je donja granica jer je parabola ispod pravca u tom komadiću, gledajući po y-osi.
|
|
| [Vrh] |
|
pedro
Forumaš(ica)
Pridružen/a: 21. 10. 2010. (14:08:21)
Postovi: (19B)16
|
| Postano: 14:52 ned, 7. 4. 2013 Naslov: |
|
|
|
[quote="fkirsek"][quote="pedro"][quote="fkirsek"][quote="pedro"]nacrtala sam si i nikak ne mogu skužiti ovo za min i max koje točke uzimam[/quote]
Pogledaj npr.jedinični kvadrat [tex][0,1]\times[0,1][/tex].
Gdje je tamo maksimum od [tex]x+y[/tex], a gdje minimum?[/quote]
joj ja sam crtala u R^2 pa mi nikak nije bilo jasno
sada je
ali možeš li pls c i d malo detaljnije objasniti
hvalaa![/quote]
Ispričavam se što duže nisam odgovarao, ipak i vaši demosi imaju kolokvije :D
Nego,
http://web.math.pmf.unizg.hr/nastava/difraf/int/2009-10/kolokvij1.pdf
4. zadatak
c) Neku drugu integralnu sumu dobiješ tako da jednostavno za svaki pravokutnik te subdivizije NE uzmeš minimum i maksimum na tom pravokutniku nego jednostavno neku drugu vrijednost.
d) Dakle, teorem srednje vrijednosti vam kaže da će za neprekidnu funkciju [tex]f[/tex] i njen integral po području [tex]A[/tex] postojati točka [tex]c[/tex] tako da je
[tex] f(c)\cdot\nu(A) = \int_A f(x) dx [/tex], gdje je [tex]\nu(A) [/tex] površina skupa [tex]A[/tex].
Sad, na prvi pogled, ne čini se da to tu koristi, jel tako? Ako to primjenimo za naš kvadrat, on će nam samo dati c za cijelo naše područje, dakle za [tex][0,2]x[0,3][/tex]. Međutim, možemo primjeniti taj teorem na svako podpodručje subdivizije posebno, dobijajću [tex]c_1, c_2,c_3, c_4[/tex] za koje vrijedi, po svakom od tih kvadrata, da je [tex]f(c_i)\cdot povrsina = \int_{pravokutnik} f(x) dx[/tex].
Kad bi zbrojili sve gornje jednadžbe, s desne strane bi dobili integral po cijelom pravokutniku [tex][0,2]x[0,3][/tex], a s lijeve integralnu sumu za taj integral.
Iako, to smo mogli i direktno. Ako se ne varam, [tex]c_i[/tex] iz gornjeg teorema će upravo biti sredine svakog od pravokutnika.
[size=9][color=#999999]Added after 32 minutes:[/color][/size]
[quote="pedro"]http://web.math.pmf.unizg.hr/nastava/difraf/int/2007-08/IFVVkol1.pdf
[/quote]
3.b)
Skoro. Ovo što si ti napisala za taj zadatak je integral po "unutrašnjosti" tog paraboloida, zapravo se traži volumen svega u cilindru OSIM tog dijela. No, pošto je volumen cilindra lako izračunati, iznosi [tex]a^3\pi[/tex], rješenje je [tex]a^3\pi - I[/tex], gdje je I integral koji si napisala.
2.
Prvi integral je dobar, u drugom x sigurno ne ide od 1 do 9 već od 1 do 3, dok su ti granice y-ona... čudne. Ne možeš imati y kao varijablu u granicama od y-on. Dakle, drugi integral bi trebao ići:
[tex]\int_0^3 \int_{x^2}^{4x+3} (x-y) dy dx[/tex]
[tex]x^2[/tex] je donja granica jer je parabola ispod pravca u tom komadiću, gledajući po y-osi.[/quote]
3. kužim :) hvala na ispravci
2,. zadatak: oprosti u drugom integralu je greška, treba prvo iči dx pa onda dy :S
lapsus, znači ovako:
[latex]\int_{0}^{9}\int_{-\sqrt{y}}^{\sqrt{y}}(x-y)dxdy - \int_{1}^{9}\int_{\frac{y+3}{4}}^{\sqrt{y}}(x-y)dxdy[/latex]
mislim da bi to sad trebalo biti ok?
[size=9][color=#999999]Added after 39 minutes:[/color][/size]
24.4.2008
4. a)
promjena granica:
[latex]\int_{0}^{\frac{\pi }{2}}\int_{1-x^{2}}^{cosx}f(x,y) dydx[/latex]
[size=9][color=#999999]Added after 7 minutes:[/color][/size]
za b)
nacrtala sam u koordinatnom polukružnice i nije mi jasno koje područje točno gledamo?
| fkirsek (napisa): | | pedro (napisa): | | fkirsek (napisa): | | pedro (napisa): | | nacrtala sam si i nikak ne mogu skužiti ovo za min i max koje točke uzimam |
Pogledaj npr.jedinični kvadrat [tex][0,1]\times[0,1][/tex].
Gdje je tamo maksimum od [tex]x+y[/tex], a gdje minimum? |
joj ja sam crtala u R^2 pa mi nikak nije bilo jasno
sada je
ali možeš li pls c i d malo detaljnije objasniti
hvalaa! |
Ispričavam se što duže nisam odgovarao, ipak i vaši demosi imaju kolokvije
Nego,
http://web.math.pmf.unizg.hr/nastava/difraf/int/2009-10/kolokvij1.pdf
4. zadatak
c) Neku drugu integralnu sumu dobiješ tako da jednostavno za svaki pravokutnik te subdivizije NE uzmeš minimum i maksimum na tom pravokutniku nego jednostavno neku drugu vrijednost.
d) Dakle, teorem srednje vrijednosti vam kaže da će za neprekidnu funkciju [tex]f[/tex] i njen integral po području [tex]A[/tex] postojati točka [tex]c[/tex] tako da je
[tex] f(c)\cdot\nu(A) = \int_A f(x) dx [/tex], gdje je [tex]\nu(A) [/tex] površina skupa [tex]A[/tex].
Sad, na prvi pogled, ne čini se da to tu koristi, jel tako? Ako to primjenimo za naš kvadrat, on će nam samo dati c za cijelo naše područje, dakle za [tex][0,2]x[0,3][/tex]. Međutim, možemo primjeniti taj teorem na svako podpodručje subdivizije posebno, dobijajću [tex]c_1, c_2,c_3, c_4[/tex] za koje vrijedi, po svakom od tih kvadrata, da je [tex]f(c_i)\cdot povrsina = \int_{pravokutnik} f(x) dx[/tex].
Kad bi zbrojili sve gornje jednadžbe, s desne strane bi dobili integral po cijelom pravokutniku [tex][0,2]x[0,3][/tex], a s lijeve integralnu sumu za taj integral.
Iako, to smo mogli i direktno. Ako se ne varam, [tex]c_i[/tex] iz gornjeg teorema će upravo biti sredine svakog od pravokutnika.
Added after 32 minutes:
| pedro (napisa): | http://web.math.pmf.unizg.hr/nastava/difraf/int/2007-08/IFVVkol1.pdf
|
3.b)
Skoro. Ovo što si ti napisala za taj zadatak je integral po "unutrašnjosti" tog paraboloida, zapravo se traži volumen svega u cilindru OSIM tog dijela. No, pošto je volumen cilindra lako izračunati, iznosi [tex]a^3\pi[/tex], rješenje je [tex]a^3\pi - I[/tex], gdje je I integral koji si napisala.
2.
Prvi integral je dobar, u drugom x sigurno ne ide od 1 do 9 već od 1 do 3, dok su ti granice y-ona... čudne. Ne možeš imati y kao varijablu u granicama od y-on. Dakle, drugi integral bi trebao ići:
[tex]\int_0^3 \int_{x^2}^{4x+3} (x-y) dy dx[/tex]
[tex]x^2[/tex] je donja granica jer je parabola ispod pravca u tom komadiću, gledajući po y-osi. |
3. kužim hvala na ispravci
2,. zadatak: oprosti u drugom integralu je greška, treba prvo iči dx pa onda dy :S
lapsus, znači ovako:
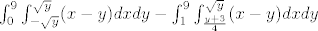
mislim da bi to sad trebalo biti ok?
Added after 39 minutes:
24.4.2008
4. a)
promjena granica:
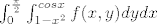
Added after 7 minutes:
za b)
nacrtala sam u koordinatnom polukružnice i nije mi jasno koje područje točno gledamo?
|
|
| [Vrh] |
|
Pepper
Forumaš(ica)
Pridružen/a: 08. 06. 2012. (02:57:26)
Postovi: (B)16
|
|
| [Vrh] |
|
fkirsek
Forumaš(ica)
Pridružen/a: 28. 09. 2012. (23:52:51)
Postovi: (23)16
|
| Postano: 17:09 ned, 7. 4. 2013 Naslov: |
|
|
|
[quote="mata"]A moze pliz pomoc oko 3. iz 2010./11.? :([/quote]
http://web.math.pmf.unizg.hr/nastava/difraf/int/2010-11/kolokvij1.pdf
Taj ti je najlakše u cilindričnim koordinatama. Primjeti, prva ploha je zapravo
[tex]x^2 + y^2 + (z - 2a)^2 = 4a[/tex], dakle sfera kojoj je središte točka [tex](0,0,2a)[/tex], a radijus [tex]2a[/tex].
Druga ploha je stožac okrenut prema gore. Za taj stožac su cilindrične koordinate posve prirodne, dobiješ jednadžbu:
[tex] az \leq 4a^2 - r^2[/tex], dok gornja jednadžba postaje:
[tex] (z-2a)^2 \leq 4a - r^2[/tex]
Dakle, granice od z-a izračunaš izravno iz tih jednadžbi, gornja je sfera, a donja je konus.
[tex]\phi[/tex] pustiš od [tex]0[/tex] do [tex]2\pi[/tex] a r pustiš od [tex]0[/tex], do radijusa kružnice u kojoj se sijeku sfera i taj stožac, a to je upravo [tex]4a[/tex] (pošto radijus uopće ne ovisi o kutu). Jacobijan znaš i to je to.
[size=9][color=#999999]Added after 4 minutes:[/color][/size]
@pedro
http://web.math.pmf.unizg.hr/nastava/difraf/int/2007-08/IFVVkol1.pdf
4.a)
čini mi se da x ipak ide od -1 do [tex]\pi/2[/tex]
b)
Čini mi se da se gleda područje većeg polukruga od kojeg je oduzet manji polukrug.
[size=9][color=#999999]Added after 2 minutes:[/color][/size]
[quote="Pepper"]jel iko rjesia 2 iz 2009 ?
iman sliku al ne znan granice :([/quote]
http://web.math.pmf.unizg.hr/nastava/difraf/int/2008-09/kolokvij1.pdf
Ako misliš na taj zadatak - hint, pređi na alternativne cilindrične koordinate:
[tex]
x = r cos \phi[/tex]
[tex]y = y[/tex]
[tex]z = r sin \phi[/tex]
[/tex]
i tako nađeš lagano granice (pošto se ipak radi o parabolama i cilindrima, za koje je poprilično jednostavno naći granice u cilindričnim koordinatama)
| mata (napisa): | A moze pliz pomoc oko 3. iz 2010./11.?  |
http://web.math.pmf.unizg.hr/nastava/difraf/int/2010-11/kolokvij1.pdf
Taj ti je najlakše u cilindričnim koordinatama. Primjeti, prva ploha je zapravo
[tex]x^2 + y^2 + (z - 2a)^2 = 4a[/tex], dakle sfera kojoj je središte točka [tex](0,0,2a)[/tex], a radijus [tex]2a[/tex].
Druga ploha je stožac okrenut prema gore. Za taj stožac su cilindrične koordinate posve prirodne, dobiješ jednadžbu:
[tex] az \leq 4a^2 - r^2[/tex], dok gornja jednadžba postaje:
[tex] (z-2a)^2 \leq 4a - r^2[/tex]
Dakle, granice od z-a izračunaš izravno iz tih jednadžbi, gornja je sfera, a donja je konus.
[tex]\phi[/tex] pustiš od [tex]0[/tex] do [tex]2\pi[/tex] a r pustiš od [tex]0[/tex], do radijusa kružnice u kojoj se sijeku sfera i taj stožac, a to je upravo [tex]4a[/tex] (pošto radijus uopće ne ovisi o kutu). Jacobijan znaš i to je to.
Added after 4 minutes:
@pedro
http://web.math.pmf.unizg.hr/nastava/difraf/int/2007-08/IFVVkol1.pdf
4.a)
čini mi se da x ipak ide od -1 do [tex]\pi/2[/tex]
b)
Čini mi se da se gleda područje većeg polukruga od kojeg je oduzet manji polukrug.
Added after 2 minutes:
| Pepper (napisa): | jel iko rjesia 2 iz 2009 ?
iman sliku al ne znan granice |
http://web.math.pmf.unizg.hr/nastava/difraf/int/2008-09/kolokvij1.pdf
Ako misliš na taj zadatak - hint, pređi na alternativne cilindrične koordinate:
[tex]
x = r cos \phi[/tex]
[tex]y = y[/tex]
[tex]z = r sin \phi[/tex]
[/tex]
i tako nađeš lagano granice (pošto se ipak radi o parabolama i cilindrima, za koje je poprilično jednostavno naći granice u cilindričnim koordinatama)
Zadnja promjena: fkirsek; 22:37 pon, 8. 4. 2013; ukupno mijenjano 1 put.
|
|
| [Vrh] |
|
mamba
Forumaš(ica)
Pridružen/a: 09. 07. 2012. (17:11:16)
Postovi: (16)16
|
| Postano: 17:56 ned, 7. 4. 2013 Naslov: |
|
|
|
[quote="pedro"]http://web.math.pmf.unizg.hr/nastava/difraf/int/2007-08/IFVVkol1.pdf
3. b)
zanima me jesam li dobro postavila granice:
[latex]\int_{0}^{2\pi }\int_{0}^{a}\int_{0}^{r^{2}} r dzdrd\varphi [/latex]
koristila sam cilindrične koordinate
[size=9][color=#999999]Added after 24 minutes:[/color][/size]
[/quote]
[quote="fkirsek"][quote="pedro"][quote="fkirsek"]
[quote="pedro"]http://web.math.pmf.unizg.hr/nastava/difraf/int/2007-08/IFVVkol1.pdf
[/quote]
3.b)
Skoro. Ovo što si ti napisala za taj zadatak je integral po "unutrašnjosti" tog paraboloida, zapravo se traži volumen svega u cilindru OSIM tog dijela. No, pošto je volumen cilindra lako izračunati, iznosi [tex]a^3\pi[/tex], rješenje je [tex]a^3\pi - I[/tex], gdje je I integral koji si napisala.
[/quote]
Kako bi onda izgledale granice za taj integral kad ga idemo izravno računati?
Meni se čini da je ovo napisano u 1. postu ok, pa zato molim da me ispravite ako griješim.
| pedro (napisa): | http://web.math.pmf.unizg.hr/nastava/difraf/int/2007-08/IFVVkol1.pdf
3. b)
zanima me jesam li dobro postavila granice:
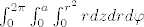
koristila sam cilindrične koordinate
Added after 24 minutes:
|
[quote="fkirsek"][quote="pedro"] | fkirsek (napisa): |
| pedro (napisa): | http://web.math.pmf.unizg.hr/nastava/difraf/int/2007-08/IFVVkol1.pdf
|
3.b)
Skoro. Ovo što si ti napisala za taj zadatak je integral po "unutrašnjosti" tog paraboloida, zapravo se traži volumen svega u cilindru OSIM tog dijela. No, pošto je volumen cilindra lako izračunati, iznosi [tex]a^3\pi[/tex], rješenje je [tex]a^3\pi - I[/tex], gdje je I integral koji si napisala.
|
Kako bi onda izgledale granice za taj integral kad ga idemo izravno računati?
Meni se čini da je ovo napisano u 1. postu ok, pa zato molim da me ispravite ako griješim.
|
|
| [Vrh] |
|
kiara
Forumaš(ica)
Pridružen/a: 15. 11. 2011. (23:22:57)
Postovi: (55)16
|
|
| [Vrh] |
|
Nightrider
Forumaš s poteškoćama u pisanju
Pridružen/a: 19. 03. 2013. (19:01:05)
Postovi: (61)16
Spol:
|
|
| [Vrh] |
|
pedro
Forumaš(ica)
Pridružen/a: 21. 10. 2010. (14:08:21)
Postovi: (19B)16
|
|
| [Vrh] |
|
kiara
Forumaš(ica)
Pridružen/a: 15. 11. 2011. (23:22:57)
Postovi: (55)16
|
|
| [Vrh] |
|
rom
Forumaš(ica)
Pridružen/a: 26. 10. 2010. (11:10:35)
Postovi: (2D)16
|
|
| [Vrh] |
|
|
