| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
If and only if
Forumaš(ica)


Pridružen/a: 30. 09. 2012. (18:16:22)
Postovi: (1F)16
Spol: 
|
|
| [Vrh] |
|
Tomislav
Forumaš(ica)

Pridružen/a: 04. 10. 2010. (20:18:25)
Postovi: (181)16
Spol: 
|
|
| [Vrh] |
|
If and only if
Forumaš(ica)


Pridružen/a: 30. 09. 2012. (18:16:22)
Postovi: (1F)16
Spol: 
|
|
| [Vrh] |
|
Tomislav
Forumaš(ica)

Pridružen/a: 04. 10. 2010. (20:18:25)
Postovi: (181)16
Spol: 
|
|
| [Vrh] |
|
rafaelm
Forumaš(ica)


Pridružen/a: 24. 12. 2006. (13:30:11)
Postovi: (21F)16
Spol: 
Lokacija: Zagreb
|
 Postano: 21:32 pet, 1. 2. 2013 Naslov: Re: Krugovi u R^2 Postano: 21:32 pet, 1. 2. 2013 Naslov: Re: Krugovi u R^2 |
    |
|
|
[quote="If and only if"]Ako na slucajan(random) nacin izaberemo beskonacan, prebrojiv skup krugova iz [latex] \mathbb R^2[/latex] takvih da svi imaju isti radijus [latex]R>1[/latex] i srediste svakog kruga ima koordinate [latex](x,y)[/latex], [latex]x,y\in\mathbb Z[/latex], kolika je vjerojatnost da je presjek svaka dva kruga iz tog skupa prazan skup?[/quote]
Zadatak nije dobro definiran, ne znamo što znači "[i]na slucajan(random) nacin izaberemo[/i]". To podrazumijeva nekakvu uniformnu mjeru na skupu svih izbora. To je OK ako je npr. skup svih mogućih izbora konačan (pa možemo gledati omjer povoljnih i mogućih događaja), ili ako je to neki "pristojan" podskup od [tex]R^n[/tex] (pa možemo gledati omjere površina/volumena). Ali za neki proizvoljan beskonačan skup (kao što je npr. skup svih prebrojivih skupova krugova konstantnog radijusa u [tex]R^2[/tex]) to ne mora imati značenja - trebaš zadati [url=http://en.wikipedia.org/wiki/Probability_measure]vjerojatnosnu mjeru[/url] na skupu svih mogućih izbora.
EDIT: Recimo, razmisli o jednostavnijem problemu: Na slučajan način izaberemo prirodan broj. Što to znači? Da je svaki broj jednako vjerojatan? Ako da, onda je vjerojatnost izvlačenja svakog pojedinog broja jednaka [tex]\frac{1}{\infty}=0[/tex], a tada bi bilo
[tex]1=P(\text{izvukli smo prirodan broj}) = P(\text{izvukli smo $1$, ili izvukli smo $2$, ili ... } ) = P(\text{izvukli smo $1$}) + P(\text{izvukli smo $2$}) + \ldots = 0 + 0 + \ldots = 0.[/tex]
| If and only if (napisa): | Ako na slucajan(random) nacin izaberemo beskonacan, prebrojiv skup krugova iz 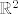 takvih da svi imaju isti radijus takvih da svi imaju isti radijus 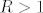 i srediste svakog kruga ima koordinate i srediste svakog kruga ima koordinate 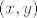 , , 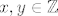 , kolika je vjerojatnost da je presjek svaka dva kruga iz tog skupa prazan skup? , kolika je vjerojatnost da je presjek svaka dva kruga iz tog skupa prazan skup? |
Zadatak nije dobro definiran, ne znamo što znači "na slucajan(random) nacin izaberemo". To podrazumijeva nekakvu uniformnu mjeru na skupu svih izbora. To je OK ako je npr. skup svih mogućih izbora konačan (pa možemo gledati omjer povoljnih i mogućih događaja), ili ako je to neki "pristojan" podskup od [tex]R^n[/tex] (pa možemo gledati omjere površina/volumena). Ali za neki proizvoljan beskonačan skup (kao što je npr. skup svih prebrojivih skupova krugova konstantnog radijusa u [tex]R^2[/tex]) to ne mora imati značenja - trebaš zadati vjerojatnosnu mjeru na skupu svih mogućih izbora.
EDIT: Recimo, razmisli o jednostavnijem problemu: Na slučajan način izaberemo prirodan broj. Što to znači? Da je svaki broj jednako vjerojatan? Ako da, onda je vjerojatnost izvlačenja svakog pojedinog broja jednaka [tex]\frac{1}{\infty}=0[/tex], a tada bi bilo
[tex]1=P(\text{izvukli smo prirodan broj}) = P(\text{izvukli smo $1$, ili izvukli smo $2$, ili ... } ) = P(\text{izvukli smo $1$}) + P(\text{izvukli smo $2$}) + \ldots = 0 + 0 + \ldots = 0.[/tex]
_________________
Rafael Mrđen
|
|
| [Vrh] |
|
If and only if
Forumaš(ica)


Pridružen/a: 30. 09. 2012. (18:16:22)
Postovi: (1F)16
Spol: 
|
 Postano: 10:11 sub, 2. 2. 2013 Naslov: Postano: 10:11 sub, 2. 2. 2013 Naslov: |
    |
|
|
[quote="Tomislav"]A imas rjesenje tog svog izmisljenog zadatka :D?[/quote] A nemam, iskreno da ti kazem, nisam jos ozbiljnije razmislio o njemu. Kolega sta se javio ispod tebe mi je svojom rekacijom da neke ideje.
[quote="rafaelm"] Ali za neki proizvoljan beskonačan skup (kao što je npr. skup svih prebrojivih skupova krugova konstantnog radijusa u [tex]R^2[/tex]) to ne mora imati značenja - trebaš zadati [url=http://en.wikipedia.org/wiki/Probability_measure]vjerojatnosnu mjeru[/url] na skupu svih mogućih izbora. [/quote]
Jasno mi je sto zelis kazat, ali bitno je i to da je dodano [tex]R>1[/tex] jer je minimalna udaljenost izmedu dvije tocke sa obje cjelobrojne koordinate jednaka [tex]1[/tex] pa da to ogranicenje na radijus nije zadano ocito bi vjerojatnost bila jednaka nula u tom slucaju, isto to nije isuvise velika proizvoljnost (a u isto vrijeme i je) jer se sredista nalaze na tockama s cjelobrojnim koordinatama. Mozda je problem dijelom i u tome sto je broj tih izbora krugova na ovako definiran nacin neprebrojiv skup pa bi vjerojatnosna mjera bila neprebrojiva suma pojedinih dogadaja. U svakom slucaju, mislim da treba pomno sagledat prirodu problema.
[quote="rafaelm"]EDIT: Recimo, razmisli o jednostavnijem problemu: Na slučajan način izaberemo prirodan broj. Što to znači? Da je svaki broj jednako vjerojatan? Ako da, onda je vjerojatnost izvlačenja svakog pojedinog broja jednaka [tex]\frac{1}{\infty}=0[/tex], a tada bi bilo
[tex]1=P(\text{izvukli smo prirodan broj}) = P(\text{izvukli smo $1$, ili izvukli smo $2$, ili ... } ) = P(\text{izvukli smo $1$}) + P(\text{izvukli smo $2$}) + \ldots = 0 + 0 + \ldots = 0.[/tex][/quote]
Izgleda u redu ali pogledaj na problem i na recimo ovakav nacin:
[tex]1=P(\text{izvukli smo prirodan broj}) = P(\text{izvukli smo paran , ili izvukli smo neparan} ) = 1/2 + 1/2=1[/tex]
EDIT: A u biti zahtjev [tex]R>1[/tex] i ne izgleda toliko bitan, on samo govori da je vjerojatnost svakog izbora u kojem su dva kruga na "susjednim" tockama jednaka nula.
:sib:
| Tomislav (napisa): | A imas rjesenje tog svog izmisljenog zadatka  ? ? |
A nemam, iskreno da ti kazem, nisam jos ozbiljnije razmislio o njemu. Kolega sta se javio ispod tebe mi je svojom rekacijom da neke ideje.
| rafaelm (napisa): | | Ali za neki proizvoljan beskonačan skup (kao što je npr. skup svih prebrojivih skupova krugova konstantnog radijusa u [tex]R^2[/tex]) to ne mora imati značenja - trebaš zadati vjerojatnosnu mjeru na skupu svih mogućih izbora. |
Jasno mi je sto zelis kazat, ali bitno je i to da je dodano [tex]R>1[/tex] jer je minimalna udaljenost izmedu dvije tocke sa obje cjelobrojne koordinate jednaka [tex]1[/tex] pa da to ogranicenje na radijus nije zadano ocito bi vjerojatnost bila jednaka nula u tom slucaju, isto to nije isuvise velika proizvoljnost (a u isto vrijeme i je) jer se sredista nalaze na tockama s cjelobrojnim koordinatama. Mozda je problem dijelom i u tome sto je broj tih izbora krugova na ovako definiran nacin neprebrojiv skup pa bi vjerojatnosna mjera bila neprebrojiva suma pojedinih dogadaja. U svakom slucaju, mislim da treba pomno sagledat prirodu problema.
| rafaelm (napisa): | EDIT: Recimo, razmisli o jednostavnijem problemu: Na slučajan način izaberemo prirodan broj. Što to znači? Da je svaki broj jednako vjerojatan? Ako da, onda je vjerojatnost izvlačenja svakog pojedinog broja jednaka [tex]\frac{1}{\infty}=0[/tex], a tada bi bilo
[tex]1=P(\text{izvukli smo prirodan broj}) = P(\text{izvukli smo $1$, ili izvukli smo $2$, ili ... } ) = P(\text{izvukli smo $1$}) + P(\text{izvukli smo $2$}) + \ldots = 0 + 0 + \ldots = 0.[/tex] |
Izgleda u redu ali pogledaj na problem i na recimo ovakav nacin:
[tex]1=P(\text{izvukli smo prirodan broj}) = P(\text{izvukli smo paran , ili izvukli smo neparan} ) = 1/2 + 1/2=1[/tex]
EDIT: A u biti zahtjev [tex]R>1[/tex] i ne izgleda toliko bitan, on samo govori da je vjerojatnost svakog izbora u kojem su dva kruga na "susjednim" tockama jednaka nula.

|
|
| [Vrh] |
|
Leolinus
Forumaš(ica)

Pridružen/a: 30. 11. 2012. (16:36:41)
Postovi: (10)16
|
 Postano: 13:11 sub, 2. 2. 2013 Naslov: Postano: 13:11 sub, 2. 2. 2013 Naslov: |
    |
|
|
[quote="If and only if"]
[tex]1=P(\text{izvukli smo prirodan broj}) = P(\text{izvukli smo paran , ili izvukli smo neparan} ) = 1/2 + 1/2=1[/tex]
EDIT: A u biti zahtjev [tex]R>1[/tex] i ne izgleda toliko bitan, on samo govori da je vjerojatnost svakog izbora u kojem su dva kruga na "susjednim" tockama jednaka nula.
:sib:[/quote]
Skup parnih, a i skup neparnih brojeva jednakobrojan je sa skupom prirodnih tako da gledajući zadatak na taj način je u potpunosti krivo jer ne postoji išta što bi reklo da parnih brojeva u skupu prirodnih ima pola.
Tvoj zadatak je sličan kao da tražiš vjerojatnost izbora neke točke unutar površine kvadrata. Jednostavno ti dimenzije nisu iste. Uvijek postoji neki izbor točke za koji se oni neće sjeći.
Recimo da imaš kvadrat neke površine N^2 i sada tražiš koliko kružnica nekog određenog radijusa možeš ubaciti, a da se ne sijeku, primijeti da kružnica ima površinu, površina kvadrata je konačna, a onda zadatak ima rješenje.
Isto bi mogao napraviti i da pozicioniraš ta središta na cjelobrojne točke.
| If and only if (napisa): |
[tex]1=P(\text{izvukli smo prirodan broj}) = P(\text{izvukli smo paran , ili izvukli smo neparan} ) = 1/2 + 1/2=1[/tex]
EDIT: A u biti zahtjev [tex]R>1[/tex] i ne izgleda toliko bitan, on samo govori da je vjerojatnost svakog izbora u kojem su dva kruga na "susjednim" tockama jednaka nula.
 |
Skup parnih, a i skup neparnih brojeva jednakobrojan je sa skupom prirodnih tako da gledajući zadatak na taj način je u potpunosti krivo jer ne postoji išta što bi reklo da parnih brojeva u skupu prirodnih ima pola.
Tvoj zadatak je sličan kao da tražiš vjerojatnost izbora neke točke unutar površine kvadrata. Jednostavno ti dimenzije nisu iste. Uvijek postoji neki izbor točke za koji se oni neće sjeći.
Recimo da imaš kvadrat neke površine N^2 i sada tražiš koliko kružnica nekog određenog radijusa možeš ubaciti, a da se ne sijeku, primijeti da kružnica ima površinu, površina kvadrata je konačna, a onda zadatak ima rješenje.
Isto bi mogao napraviti i da pozicioniraš ta središta na cjelobrojne točke.
|
|
| [Vrh] |
|
Tomislav
Forumaš(ica)

Pridružen/a: 04. 10. 2010. (20:18:25)
Postovi: (181)16
Spol: 
|
|
| [Vrh] |
|
Nightrider
Forumaš s poteškoćama u pisanju


Pridružen/a: 19. 03. 2013. (19:01:05)
Postovi: (61)16
Spol: 
|
 Postano: 19:11 pon, 8. 4. 2013 Naslov: Re: Krugovi u R^2 Postano: 19:11 pon, 8. 4. 2013 Naslov: Re: Krugovi u R^2 |
    |
|
|
[quote="rafaelm"]EDIT: Recimo, razmisli o jednostavnijem problemu: Na slučajan način izaberemo prirodan broj. Što to znači? Da je svaki broj jednako vjerojatan? Ako da, onda je vjerojatnost izvlačenja svakog pojedinog broja jednaka [tex]\frac{1}{\infty}=0[/tex], a tada bi bilo
[tex]1=P(\text{izvukli smo prirodan broj}) = P(\text{izvukli smo $1$, ili izvukli smo $2$, ili ... } ) = P(\text{izvukli smo $1$}) + P(\text{izvukli smo $2$}) + \ldots = 0 + 0 + \ldots = 0.[/tex][/quote]
To je stvar stila i ukusa, ajde ti meni zabrani da ja tvoj rezultat zapisem ovako: [tex]1=P(\text{izvukli smo prirodan broj}) = P(\text{izvukli smo $1$, ili izvukli smo $2$, ili ... } ) = P(\text{izvukli smo $1$}) + P(\text{izvukli smo $2$}) + \ldots =\frac {1}{\infty}+ \frac {1}{\infty}+...=\infty \cdot \frac {1}{\infty}=1[/tex]. Mozda bi bilo dobro odustat od pretpostavke da je svaki broj jednako vjerojatan.
[quote="Leolinus"]
Skup parnih, a i skup neparnih brojeva jednakobrojan je sa skupom prirodnih tako da gledajući zadatak na taj način je u potpunosti krivo jer ne postoji išta što bi reklo da parnih brojeva u skupu prirodnih ima pola.[/quote]
Ne postoji [color=red]tebi[/color]. Bijektivni princip usporedjivanja skupova daje neku "sliku o brojnosti elemenata u nekom skupu" i onda izranjaju razlicite kardinalnosti. No bas zato sta je skup prirodnih brojeva istog kardinaliteta ko i skup parnih brojeva moze se usporedjivat UDIO parnih brojeva u svim prirodnim. I parnih brojeva ima tocno pola u skupu prirodnih brojeva. Isto ko sta ih djeljivih sa 5 ima tocno jedna petina.
[quote="Tomislav"] Ako postoji barem 1 slucaj u kojem neka definicija nema smisla, onda ona nema smisla i gotovo. [/quote]
Tebe necu demantirat jer djelujes dobar.
[b](i neka se ovo pribaci u Cistiliste jer nije direktno vezano uz kolegij)[/b]
| rafaelm (napisa): | EDIT: Recimo, razmisli o jednostavnijem problemu: Na slučajan način izaberemo prirodan broj. Što to znači? Da je svaki broj jednako vjerojatan? Ako da, onda je vjerojatnost izvlačenja svakog pojedinog broja jednaka [tex]\frac{1}{\infty}=0[/tex], a tada bi bilo
[tex]1=P(\text{izvukli smo prirodan broj}) = P(\text{izvukli smo $1$, ili izvukli smo $2$, ili ... } ) = P(\text{izvukli smo $1$}) + P(\text{izvukli smo $2$}) + \ldots = 0 + 0 + \ldots = 0.[/tex] |
To je stvar stila i ukusa, ajde ti meni zabrani da ja tvoj rezultat zapisem ovako: [tex]1=P(\text{izvukli smo prirodan broj}) = P(\text{izvukli smo $1$, ili izvukli smo $2$, ili ... } ) = P(\text{izvukli smo $1$}) + P(\text{izvukli smo $2$}) + \ldots =\frac {1}{\infty}+ \frac {1}{\infty}+...=\infty \cdot \frac {1}{\infty}=1[/tex]. Mozda bi bilo dobro odustat od pretpostavke da je svaki broj jednako vjerojatan.
| Leolinus (napisa): |
Skup parnih, a i skup neparnih brojeva jednakobrojan je sa skupom prirodnih tako da gledajući zadatak na taj način je u potpunosti krivo jer ne postoji išta što bi reklo da parnih brojeva u skupu prirodnih ima pola. |
Ne postoji tebi. Bijektivni princip usporedjivanja skupova daje neku "sliku o brojnosti elemenata u nekom skupu" i onda izranjaju razlicite kardinalnosti. No bas zato sta je skup prirodnih brojeva istog kardinaliteta ko i skup parnih brojeva moze se usporedjivat UDIO parnih brojeva u svim prirodnim. I parnih brojeva ima tocno pola u skupu prirodnih brojeva. Isto ko sta ih djeljivih sa 5 ima tocno jedna petina.
| Tomislav (napisa): | | Ako postoji barem 1 slucaj u kojem neka definicija nema smisla, onda ona nema smisla i gotovo. |
Tebe necu demantirat jer djelujes dobar.
(i neka se ovo pribaci u Cistiliste jer nije direktno vezano uz kolegij)
|
|
| [Vrh] |
|
Tomislav
Forumaš(ica)

Pridružen/a: 04. 10. 2010. (20:18:25)
Postovi: (181)16
Spol: 
|
|
| [Vrh] |
|
satja
Forumaš(ica)

Pridružen/a: 16. 05. 2010. (10:44:17)
Postovi: (F1)16
|
 Postano: 10:55 uto, 9. 4. 2013 Naslov: Re: Krugovi u R^2 Postano: 10:55 uto, 9. 4. 2013 Naslov: Re: Krugovi u R^2 |
    |
|
|
[quote="Nightrider"] No bas zato sta je skup prirodnih brojeva istog kardinaliteta ko i skup parnih brojeva moze se usporedjivat UDIO parnih brojeva u svim prirodnim. I parnih brojeva ima tocno pola u skupu prirodnih brojeva. Isto ko sta ih djeljivih sa 5 ima tocno jedna petina.[/quote]
Zbilja? A što ako skup prirodnih brojeva napišeš ovako:
N = {1, 3, 5, 2, 7, 9, 11, 4, ...} -- dakle, tri neparna, pa jedan parni, pa tri neparna, pa jedan parni, i tako dalje.
To je još uvijek isti skup (kao što su npr. skupovi {a, b} i {b, a} isti), ali čini se da (tvojom terminologijom) "udio" parnih brojeva nije pola.
| Nightrider (napisa): | | No bas zato sta je skup prirodnih brojeva istog kardinaliteta ko i skup parnih brojeva moze se usporedjivat UDIO parnih brojeva u svim prirodnim. I parnih brojeva ima tocno pola u skupu prirodnih brojeva. Isto ko sta ih djeljivih sa 5 ima tocno jedna petina. |
Zbilja? A što ako skup prirodnih brojeva napišeš ovako:
N = {1, 3, 5, 2, 7, 9, 11, 4, ...} – dakle, tri neparna, pa jedan parni, pa tri neparna, pa jedan parni, i tako dalje.
To je još uvijek isti skup (kao što su npr. skupovi {a, b} i {b, a} isti), ali čini se da (tvojom terminologijom) "udio" parnih brojeva nije pola.
|
|
| [Vrh] |
|
Nightrider
Forumaš s poteškoćama u pisanju


Pridružen/a: 19. 03. 2013. (19:01:05)
Postovi: (61)16
Spol: 
|
 Postano: 13:00 uto, 9. 4. 2013 Naslov: Postano: 13:00 uto, 9. 4. 2013 Naslov: |
    |
|
|
[quote="Tomislav"]Za pocetak, komentar na quote od rafaelm nema apsolutno nikakvog smisla... dalje nisam imao volje citati...[/quote]
Nema [b]tebi[/b]. Sad cu i tebe demantirat jer si povodljiv.
[quote="Tomislav"] Ako postoji barem 1 slucaj u kojem neka definicija nema smisla, onda ona nema smisla i gotovo. :?[/quote]
Ovo je toliko besmislena izjava da se jednostavno moras zapitat kad ovakvo sto procitas.
Bit definicije je da sto je moguce jasnije svojim sadrzajem obuhvati odredjeni skup objekata tako da se moze, rabeci definiciju, razlucit da li nesto pripada ili ne pripada tom skupu objekata.
Tako da NEMOZE postojat slucaj u kojem definicija nema smisla jer je takodjer jedan od prvih uvjeta na dobru i valjanu definiciju taj da je ona SMISLENA.
Primjer: Broj je prost ako i samo ako su mu jedini djelitelji broj 1 i on sam. (ova definicija sluzi da se razluci pojam slozenog i pojam prostog broja i da uvede pojam prostog broja).
Primjer 2: Funkcija je neprekidna u x_0 ako i samo ako za svaki epsilon>0 postoji delta>0 takav da cim je |x-x_0|<delta tada je |f(x)-f(x_0)|<epsilon (ova definicija sluzi da razlucimo u tocki prekinute od u tocki neprekinutih funkcija i da uvedemo pojam u tocki neprekidne funkcije).
Primjer 3: Skup A\B je skup koji se sastoji od onih elemenata koji su u skupu A i koji nisu u skupu B (ova definicija sluzi da razlucimo koji je to skup "razlika skupova A i B" od svih mogucih skupova koje mozemo dobiti operiranjem nad skupovima A i B i da uvede binarnu operaciju "razlika skupova" ).
Mudrome dosta.
[quote="satja"][quote="Nightrider"] No bas zato sta je skup prirodnih brojeva istog kardinaliteta ko i skup parnih brojeva moze se usporedjivat UDIO parnih brojeva u svim prirodnim. I parnih brojeva ima tocno pola u skupu prirodnih brojeva. Isto ko sta ih djeljivih sa 5 ima tocno jedna petina.[/quote]
Zbilja? A što ako skup prirodnih brojeva napišeš ovako:
N = {1, 3, 5, 2, 7, 9, 11, 4, ...} -- dakle, tri neparna, pa jedan parni, pa tri neparna, pa jedan parni, i tako dalje.
To je još uvijek isti skup (kao što su npr. skupovi {a, b} i {b, a} isti), ali čini se da (tvojom terminologijom) "udio" parnih brojeva nije pola.[/quote]
Odlicna primjedba. Izgleda mi i da ti je jasno da sam ja mislio na prirodni poredak skupa N={1,2,3,4...}. I stvarno, ako se promatra prirodni poredak onda se moze jednostavno dokazat da ima tocno pola parnih brojeva u skupu prirodnih brojeva.
Mozemo nastavit (a i ne moramo) s detaljima oko definicije skupa prirodnih brojeva, ako idemo na Peanovu aksiomatizaciju onda je u karakterizaciji skupa prirodnih brojeva sadrzana funkcija "sljedbenik broja" definirana sa S(n)=n+1, i time tvoj skup nije skup prirodnih brojeva, premda u isto vrijeme i jest skup prirodnih brojeva ako idemo na definiciju da su dva skupa jednaka ako i samo ako se oni sastoje od istih elemenata, tako da ulazimo u logicke poteskoce.
| Tomislav (napisa): | | Za pocetak, komentar na quote od rafaelm nema apsolutno nikakvog smisla... dalje nisam imao volje citati... |
Nema tebi. Sad cu i tebe demantirat jer si povodljiv.
| Tomislav (napisa): | Ako postoji barem 1 slucaj u kojem neka definicija nema smisla, onda ona nema smisla i gotovo.  |
Ovo je toliko besmislena izjava da se jednostavno moras zapitat kad ovakvo sto procitas.
Bit definicije je da sto je moguce jasnije svojim sadrzajem obuhvati odredjeni skup objekata tako da se moze, rabeci definiciju, razlucit da li nesto pripada ili ne pripada tom skupu objekata.
Tako da NEMOZE postojat slucaj u kojem definicija nema smisla jer je takodjer jedan od prvih uvjeta na dobru i valjanu definiciju taj da je ona SMISLENA.
Primjer: Broj je prost ako i samo ako su mu jedini djelitelji broj 1 i on sam. (ova definicija sluzi da se razluci pojam slozenog i pojam prostog broja i da uvede pojam prostog broja).
Primjer 2: Funkcija je neprekidna u x_0 ako i samo ako za svaki epsilon>0 postoji delta>0 takav da cim je |x-x_0|<delta tada je |f(x)-f(x_0)|<epsilon (ova definicija sluzi da razlucimo u tocki prekinute od u tocki neprekinutih funkcija i da uvedemo pojam u tocki neprekidne funkcije).
Primjer 3: Skup A\B je skup koji se sastoji od onih elemenata koji su u skupu A i koji nisu u skupu B (ova definicija sluzi da razlucimo koji je to skup "razlika skupova A i B" od svih mogucih skupova koje mozemo dobiti operiranjem nad skupovima A i B i da uvede binarnu operaciju "razlika skupova" ).
Mudrome dosta.
| satja (napisa): | | Nightrider (napisa): | | No bas zato sta je skup prirodnih brojeva istog kardinaliteta ko i skup parnih brojeva moze se usporedjivat UDIO parnih brojeva u svim prirodnim. I parnih brojeva ima tocno pola u skupu prirodnih brojeva. Isto ko sta ih djeljivih sa 5 ima tocno jedna petina. |
Zbilja? A što ako skup prirodnih brojeva napišeš ovako:
N = {1, 3, 5, 2, 7, 9, 11, 4, ...} – dakle, tri neparna, pa jedan parni, pa tri neparna, pa jedan parni, i tako dalje.
To je još uvijek isti skup (kao što su npr. skupovi {a, b} i {b, a} isti), ali čini se da (tvojom terminologijom) "udio" parnih brojeva nije pola. |
Odlicna primjedba. Izgleda mi i da ti je jasno da sam ja mislio na prirodni poredak skupa N={1,2,3,4...}. I stvarno, ako se promatra prirodni poredak onda se moze jednostavno dokazat da ima tocno pola parnih brojeva u skupu prirodnih brojeva.
Mozemo nastavit (a i ne moramo) s detaljima oko definicije skupa prirodnih brojeva, ako idemo na Peanovu aksiomatizaciju onda je u karakterizaciji skupa prirodnih brojeva sadrzana funkcija "sljedbenik broja" definirana sa S(n)=n+1, i time tvoj skup nije skup prirodnih brojeva, premda u isto vrijeme i jest skup prirodnih brojeva ako idemo na definiciju da su dva skupa jednaka ako i samo ako se oni sastoje od istih elemenata, tako da ulazimo u logicke poteskoce.
|
|
| [Vrh] |
|
Tomislav
Forumaš(ica)

Pridružen/a: 04. 10. 2010. (20:18:25)
Postovi: (181)16
Spol: 
|
|
| [Vrh] |
|
satja
Forumaš(ica)

Pridružen/a: 16. 05. 2010. (10:44:17)
Postovi: (F1)16
|
|
| [Vrh] |
|
Nightrider
Forumaš s poteškoćama u pisanju


Pridružen/a: 19. 03. 2013. (19:01:05)
Postovi: (61)16
Spol: 
|
 Postano: 13:22 uto, 9. 4. 2013 Naslov: Postano: 13:22 uto, 9. 4. 2013 Naslov: |
    |
|
|
[quote="Tomislav"]1. Zelis reci da je onaj tvoj racun sa beskonacnom sumom ok? Takodjer obrazlozi kakvog smisla ima tvoj komentar na quote of rafaelm, jer on opet, nema APSOLUTNO NIKAKVOG smisla.
2. Posto ocito ne citas kako treba, da ponovim. Ako definiras nesto i mozes naci neki primjer za koji ta definicija nije dobra, onda to nije dobra definicija.
Sama definicija ne povlaci da je ona dobra... to je valjda jasno... Lako je pronaci primjer definicije koja nije dobra.
3. Skup nema poredak.[/quote]
1. Daj mi jedan razlog zasto je racun sa beskonacnom sumom od rafaelm-a ispravniji od moga? Zasto nema smisla da ja njegovu sumu promatram kako izraz oblika [latex]\infty \cdot 0[/latex] koji je neodredjen i moze imat bilo koju vrijednost? Ja sam namjerno izabra vrijednost 1.
2. Ne zanimaju me lose definicije. Definicija za koju postoji primjer za koji ta definicija nije dobra nije definicija definicije vec, rekli bi na engleskom govornom podrucju: "piece of shit".
3. Jesi cuo za skupove koji se nazivaju "parcijalno uredjeni skupovi" ili "totalno uredjeni skupovi"?
[size=9][color=#999999]Added after 5 minutes:[/color][/size]
[quote="satja"][quote="Nightrider"] I stvarno, ako se promatra prirodni poredak onda se moze jednostavno dokazat da ima tocno pola parnih brojeva u skupu prirodnih brojeva.[/quote]
Onda te molim da nam napišeš taj dokaz, ali prije toga precizno iskažeš tvrdnju koju dokazuješ, tj. što točno znači da ih ima pola.[/quote]
Pokusaj sam to dokazat, izrazavas se dovoljno jasno i pametno da mislim da i sam mozes pronac nacin da to dokazes.
| Tomislav (napisa): | 1. Zelis reci da je onaj tvoj racun sa beskonacnom sumom ok? Takodjer obrazlozi kakvog smisla ima tvoj komentar na quote of rafaelm, jer on opet, nema APSOLUTNO NIKAKVOG smisla.
2. Posto ocito ne citas kako treba, da ponovim. Ako definiras nesto i mozes naci neki primjer za koji ta definicija nije dobra, onda to nije dobra definicija.
Sama definicija ne povlaci da je ona dobra... to je valjda jasno... Lako je pronaci primjer definicije koja nije dobra.
3. Skup nema poredak. |
1. Daj mi jedan razlog zasto je racun sa beskonacnom sumom od rafaelm-a ispravniji od moga? Zasto nema smisla da ja njegovu sumu promatram kako izraz oblika  koji je neodredjen i moze imat bilo koju vrijednost? Ja sam namjerno izabra vrijednost 1. koji je neodredjen i moze imat bilo koju vrijednost? Ja sam namjerno izabra vrijednost 1.
2. Ne zanimaju me lose definicije. Definicija za koju postoji primjer za koji ta definicija nije dobra nije definicija definicije vec, rekli bi na engleskom govornom podrucju: "piece of shit".
3. Jesi cuo za skupove koji se nazivaju "parcijalno uredjeni skupovi" ili "totalno uredjeni skupovi"?
Added after 5 minutes:
| satja (napisa): | | Nightrider (napisa): | | I stvarno, ako se promatra prirodni poredak onda se moze jednostavno dokazat da ima tocno pola parnih brojeva u skupu prirodnih brojeva. |
Onda te molim da nam napišeš taj dokaz, ali prije toga precizno iskažeš tvrdnju koju dokazuješ, tj. što točno znači da ih ima pola. |
Pokusaj sam to dokazat, izrazavas se dovoljno jasno i pametno da mislim da i sam mozes pronac nacin da to dokazes.
|
|
| [Vrh] |
|
satja
Forumaš(ica)

Pridružen/a: 16. 05. 2010. (10:44:17)
Postovi: (F1)16
|
|
| [Vrh] |
|
Tomislav
Forumaš(ica)

Pridružen/a: 04. 10. 2010. (20:18:25)
Postovi: (181)16
Spol: 
|
|
| [Vrh] |
|
Nightrider
Forumaš s poteškoćama u pisanju


Pridružen/a: 19. 03. 2013. (19:01:05)
Postovi: (61)16
Spol: 
|
 Postano: 13:41 uto, 9. 4. 2013 Naslov: Postano: 13:41 uto, 9. 4. 2013 Naslov: |
    |
|
|
[quote="satja"][quote="Nightrider"]Pokusaj sam to dokazat, izrazavas se dovoljno jasno i pametno da mislim da i sam mozes pronac nacin da to dokazes.[/quote]
Ja to ne znam dokazati, prvenstveno zato jer ne znam sto to uopce znaci.[/quote]
Dobro, zelim ti ispunit zelju pa evo:
Promatrajmo skup prirodnih brojeva sa svojim prirodnim poretkom, dakle skup N={1,2,3,4,...}. Definirajmo funkciju f na sliijedeci nacin f(n)=broj parnih brojeva u skupu {1,2,3,...,n}. Imamo dva slucaja:
1) Ako je n=2k onda imamo f(n)=f(2k)=k
2) Ako je n=2k+1 onda opet imamo f(n)=f(2k+1)=k.
Definirajmo "udio parnih brojeva u skupu prirodnih brojeva do broja n" kao [latex]g(n)= \frac {f(n)}{n}[/latex].
Promatrajmo oba slucaja:
1) Ako je n=2k onda imamo [latex]g(2k)= \frac {f(2k)}{2k}= \frac {k}{2k}= \frac {1}{2}[/latex]
2) Ako je n=2k+1 onda imamo [latex]g(2k+1)= \frac {f(2k+1)}{2k+1}= \frac {k}{2k+1}[/latex].
Ukupni udio parnih brojeva u skupu prirodnih brojeva je ocito [latex]\lim_{k\to\infty} g(k)= \frac {1}{2}[/latex].
| satja (napisa): | | Nightrider (napisa): | | Pokusaj sam to dokazat, izrazavas se dovoljno jasno i pametno da mislim da i sam mozes pronac nacin da to dokazes. |
Ja to ne znam dokazati, prvenstveno zato jer ne znam sto to uopce znaci. |
Dobro, zelim ti ispunit zelju pa evo:
Promatrajmo skup prirodnih brojeva sa svojim prirodnim poretkom, dakle skup N={1,2,3,4,...}. Definirajmo funkciju f na sliijedeci nacin f(n)=broj parnih brojeva u skupu {1,2,3,...,n}. Imamo dva slucaja:
1) Ako je n=2k onda imamo f(n)=f(2k)=k
2) Ako je n=2k+1 onda opet imamo f(n)=f(2k+1)=k.
Definirajmo "udio parnih brojeva u skupu prirodnih brojeva do broja n" kao 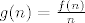 . .
Promatrajmo oba slucaja:
1) Ako je n=2k onda imamo 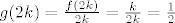
2) Ako je n=2k+1 onda imamo 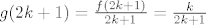 . .
Ukupni udio parnih brojeva u skupu prirodnih brojeva je ocito 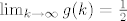 . .
|
|
| [Vrh] |
|
Tomislav
Forumaš(ica)

Pridružen/a: 04. 10. 2010. (20:18:25)
Postovi: (181)16
Spol: 
|
|
| [Vrh] |
|
Nightrider
Forumaš s poteškoćama u pisanju


Pridružen/a: 19. 03. 2013. (19:01:05)
Postovi: (61)16
Spol: 
|
 Postano: 13:54 uto, 9. 4. 2013 Naslov: Postano: 13:54 uto, 9. 4. 2013 Naslov: |
    |
|
|
[quote="Tomislav"]Posto ocito ne citas kako treba, da ponovim. [/quote]
[quote="Nightrider"]Promatrajmo skup prirodnih brojeva sa svojim prirodnim poretkom, dakle skup N={1,2,3,4,...}. [/quote]
[quote="Tomislav"]Npr sad ti je valjda jasno da tvoja definicija udjela nema smisla.... tj. kako bis ti rekao "piece of shit". (A nema smisla jer na ovaj nacin, skup N zapisan onako kako je satja napisao ne daje limes 1/2).[/quote]
I ja onda ne citam kako treba? Ti meni prvo govoris da ne citam kako treba, onda ja napisem da promatramo skup prirodnih brojeva sa svojim prirodnim poretkom (i uz tu pretpostavku definiram udio i dokazem da je jednak 1/2) i onda mi kazes da skup prirodnih brojeva definiran na satjin nacin ne daje limes 1/2 premda sam ja u dokazu koristio skup prirodnih brojeva sa svojim prirodnim poretkom? I tko onda tu ne cita kako treba?
| Tomislav (napisa): | | Posto ocito ne citas kako treba, da ponovim. |
| Nightrider (napisa): | | Promatrajmo skup prirodnih brojeva sa svojim prirodnim poretkom, dakle skup N={1,2,3,4,...}. |
| Tomislav (napisa): | | Npr sad ti je valjda jasno da tvoja definicija udjela nema smisla.... tj. kako bis ti rekao "piece of shit". (A nema smisla jer na ovaj nacin, skup N zapisan onako kako je satja napisao ne daje limes 1/2). |
I ja onda ne citam kako treba? Ti meni prvo govoris da ne citam kako treba, onda ja napisem da promatramo skup prirodnih brojeva sa svojim prirodnim poretkom (i uz tu pretpostavku definiram udio i dokazem da je jednak 1/2) i onda mi kazes da skup prirodnih brojeva definiran na satjin nacin ne daje limes 1/2 premda sam ja u dokazu koristio skup prirodnih brojeva sa svojim prirodnim poretkom? I tko onda tu ne cita kako treba?
|
|
| [Vrh] |
|
|




















