| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
Nightrider
Forumaš s poteškoćama u pisanju


Pridružen/a: 19. 03. 2013. (19:01:05)
Postovi: (61)16
Spol: 
|
 Postano: 18:12 pon, 8. 4. 2013 Naslov: Postano: 18:12 pon, 8. 4. 2013 Naslov: |
    |
|
|
[quote="kiara"][quote="Nightrider"]
Ostavio je Leibnitz jedno [url=http://en.wikipedia.org/wiki/Leibniz_integral_rule]pravilo[/url] prije nego se pridruzio svojim precima.
Ocito je [latex]f(x,t)[/latex](ova pod integralom) neprekidna kao kompozicija neprekidnih funkcija bas kao i [latex]\partial x f(x,t)[/latex] kao produkt neprekidne i neprekidne i granice [latex]g(x)=x^2[/latex] i [latex]h(x)=2x[/latex] imaju neprekidne derivacije i to ti je dovoljno da ova tvoja [latex]F[/latex] bude derivabilna.[/quote]
Oprosti,krivo sam napisala,za 1.b) ako moze pomoc?[/quote]
Ajme, dobio sam neki parametarski oblik ove spirale u (x,y) kartezijevom sustavu i gadno mi izgleda, cak se mozda izgubila diferencijabilnost u jednoj tocki jer se slomila krivulja u toj tocki, tuzno izgleda pa je bolje da ju ne pokazujem. Sta si ti probala? :D
| kiara (napisa): | | Nightrider (napisa): |
Ostavio je Leibnitz jedno pravilo prije nego se pridruzio svojim precima.
Ocito je 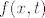 (ova pod integralom) neprekidna kao kompozicija neprekidnih funkcija bas kao i (ova pod integralom) neprekidna kao kompozicija neprekidnih funkcija bas kao i  kao produkt neprekidne i neprekidne i granice kao produkt neprekidne i neprekidne i granice  i i 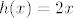 imaju neprekidne derivacije i to ti je dovoljno da ova tvoja imaju neprekidne derivacije i to ti je dovoljno da ova tvoja 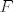 bude derivabilna. bude derivabilna. |
Oprosti,krivo sam napisala,za 1.b) ako moze pomoc? |
Ajme, dobio sam neki parametarski oblik ove spirale u (x,y) kartezijevom sustavu i gadno mi izgleda, cak se mozda izgubila diferencijabilnost u jednoj tocki jer se slomila krivulja u toj tocki, tuzno izgleda pa je bolje da ju ne pokazujem. Sta si ti probala? 
|
|
| [Vrh] |
|
kiara
Forumaš(ica)

Pridružen/a: 15. 11. 2011. (23:22:57)
Postovi: (55)16
|
 Postano: 18:52 pon, 8. 4. 2013 Naslov: Postano: 18:52 pon, 8. 4. 2013 Naslov: |
    |
|
|
[quote="rom"][tex]\int_{0}^{1}\int_{y}^{1}x^2+y^2dxdy[/tex] za [tex]x = u+ v, y=u-v[/tex], dobijem [tex]u=\frac{1}{2}(x+y)[/tex] i [tex]v=\frac{1}{2}(x-y)[/tex], i sada ne znam odrediti granice za [tex]u[/tex] i [tex]v[/tex] ako je ovo prije uopce dobro :D, hvala[/quote]
Imas g(u,v)=(x,y)=(u+v,u-v).
Kad nacrtas podrucje integracije dobijes trokut (0,0),(1,0),(1,1) u xy sustavu pa moras gledati granice
kad je y=0 (tu dobis onda u=v,x=2u tj. u=x/2 pa dobis da je u od 0 do 1/2 jer je x od 0 do 1, za pravac u=v),
x=1 (v=1-u,y=2u-1 tj. u=(y+1)/2 pa je u od 1/2 do 1 za pravac v=1-u),
i y=x (u+v=u-v tj. v=0,i u=x ili u=y pa dobis da je u od 0 do 1) i kad nacrtas u
uv sustavu dobis trokut sa vrhovima u (0,0),(1,0),(1/2,1/2) pa su
ti granice za u od 0 do 1,a za fiksan u je v od u do 1-u i racunas integral
od 2u^2+2v^2
[size=9][color=#999999]Added after 1 minutes:[/color][/size]
[/quote] Ajme, dobio sam neki parametarski oblik ove spirale u (x,y) kartezijevom sustavu i gadno mi izgleda, cak se mozda izgubila diferencijabilnost u jednoj tocki jer se slomila krivulja u toj tocki, tuzno izgleda pa je bolje da ju ne pokazujem. Sta si ti probala? :D[/quote]
Nisam znala,zato i pitam :D
| rom (napisa): | [tex]\int_{0}^{1}\int_{y}^{1}x^2+y^2dxdy[/tex] za [tex]x = u+ v, y=u-v[/tex], dobijem [tex]u=\frac{1}{2}(x+y)[/tex] i [tex]v=\frac{1}{2}(x-y)[/tex], i sada ne znam odrediti granice za [tex]u[/tex] i [tex]v[/tex] ako je ovo prije uopce dobro  , hvala , hvala |
Imas g(u,v)=(x,y)=(u+v,u-v).
Kad nacrtas podrucje integracije dobijes trokut (0,0),(1,0),(1,1) u xy sustavu pa moras gledati granice
kad je y=0 (tu dobis onda u=v,x=2u tj. u=x/2 pa dobis da je u od 0 do 1/2 jer je x od 0 do 1, za pravac u=v),
x=1 (v=1-u,y=2u-1 tj. u=(y+1)/2 pa je u od 1/2 do 1 za pravac v=1-u),
i y=x (u+v=u-v tj. v=0,i u=x ili u=y pa dobis da je u od 0 do 1) i kad nacrtas u
uv sustavu dobis trokut sa vrhovima u (0,0),(1,0),(1/2,1/2) pa su
ti granice za u od 0 do 1,a za fiksan u je v od u do 1-u i racunas integral
od 2u^2+2v^2
Added after 1 minutes:
[/quote] Ajme, dobio sam neki parametarski oblik ove spirale u (x,y) kartezijevom sustavu i gadno mi izgleda, cak se mozda izgubila diferencijabilnost u jednoj tocki jer se slomila krivulja u toj tocki, tuzno izgleda pa je bolje da ju ne pokazujem. Sta si ti probala?  [/quote] [/quote]
Nisam znala,zato i pitam 
|
|
| [Vrh] |
|
pedro
Forumaš(ica)

Pridružen/a: 21. 10. 2010. (14:08:21)
Postovi: (19B)16
|
|
| [Vrh] |
|
Nightrider
Forumaš s poteškoćama u pisanju


Pridružen/a: 19. 03. 2013. (19:01:05)
Postovi: (61)16
Spol: 
|
 Postano: 19:38 pon, 8. 4. 2013 Naslov: Postano: 19:38 pon, 8. 4. 2013 Naslov: |
    |
|
|
[quote] Ajme, dobio sam neki parametarski oblik ove spirale u (x,y) kartezijevom sustavu i gadno mi izgleda, cak se mozda izgubila diferencijabilnost u jednoj tocki jer se slomila krivulja u toj tocki, tuzno izgleda pa je bolje da ju ne pokazujem. Sta si ti probala? :D[/quote]
[quote="kiara"]
Nisam znala,zato i pitam :D[/quote]
Pogledaj zadnju sliku [url=http://www.wolframalpha.com/input/?i=%28sqrt%5Bw%2F%281%2Btg%5E2w%29%5D%2Csqrt%5Bwtg%5E2w%2F%281%2Btg%5E2w%29%5D%29%3B+w+in+%5Bo%2Cpi%5D]ovdje[/url]. Vidis da ona prikazuje krivulju koja izgleda bas kao spirala samo sta se jadna slomila kad je dotakla y-os pa se odbila od y-osi i vratila nazad u prvi kvadrant a mi bi je volili vidit u drugom kvadrantu. No razlog zasto je nema u drugom kvadrantu je vjerojatno taj sta je ona parametarski zadana pomocu korijena pa se uzima samo pozitivna vrijednost. Pokusaj sad to integrirat po formuli za volumen tijela nastao rotacijom krivulje oko x-osi koja je prikazana u parametarskom obliku, imas x(w)=sqrt(w/(1+tg^2w) i y(w)=sqrt(wtg^2w/(1+tg^2w), ovaj w je u stvari ovaj tvoj fi sta ide od nula do pi, a i ne tribam ti pisat formule, imas ih kad otvoris link odma na vrhu.
| Citat: | Ajme, dobio sam neki parametarski oblik ove spirale u (x,y) kartezijevom sustavu i gadno mi izgleda, cak se mozda izgubila diferencijabilnost u jednoj tocki jer se slomila krivulja u toj tocki, tuzno izgleda pa je bolje da ju ne pokazujem. Sta si ti probala?  |
| kiara (napisa): |
Nisam znala,zato i pitam  |
Pogledaj zadnju sliku ovdje. Vidis da ona prikazuje krivulju koja izgleda bas kao spirala samo sta se jadna slomila kad je dotakla y-os pa se odbila od y-osi i vratila nazad u prvi kvadrant a mi bi je volili vidit u drugom kvadrantu. No razlog zasto je nema u drugom kvadrantu je vjerojatno taj sta je ona parametarski zadana pomocu korijena pa se uzima samo pozitivna vrijednost. Pokusaj sad to integrirat po formuli za volumen tijela nastao rotacijom krivulje oko x-osi koja je prikazana u parametarskom obliku, imas x(w)=sqrt(w/(1+tg^2w) i y(w)=sqrt(wtg^2w/(1+tg^2w), ovaj w je u stvari ovaj tvoj fi sta ide od nula do pi, a i ne tribam ti pisat formule, imas ih kad otvoris link odma na vrhu.
|
|
| [Vrh] |
|
Pepper
Forumaš(ica)
Pridružen/a: 08. 06. 2012. (02:57:26)
Postovi: (B)16
|
|
| [Vrh] |
|
kiara
Forumaš(ica)

Pridružen/a: 15. 11. 2011. (23:22:57)
Postovi: (55)16
|
 Postano: 21:18 pon, 8. 4. 2013 Naslov: Postano: 21:18 pon, 8. 4. 2013 Naslov: |
    |
|
|
[quote="fkirsek"][quote="mata"]A moze pliz pomoc oko 3. iz 2010./11.? :([/quote]
http://web.math.pmf.unizg.hr/nastava/difraf/int/2010-11/kolokvij1.pdf
Taj ti je najlakše u cilindričnim koordinatama. Primjeti, prva ploha je zapravo
[tex]x^2 + y^2 + (z - 2a)^2 = 4a[/tex], dakle sfera kojoj je središte točka [tex](0,0,2a)[/tex], a radijus [tex]2a[/tex].
Druga ploha je stožac okrenut prema gore. Za taj stožac su cilindrične koordinate posve prirodne, dobiješ jednadžbu:
[tex] az \leq 4a^2 - r^2[/tex], dok gornja jednadžba postaje:
[tex] (z-2a)^2 \leq 4a - r^2[/tex]
Dakle, granice od z-a izračunaš izravno iz tih jednadžbi, gornja je sfera, a donja je konus.
[tex]\phi[/tex] pustiš od [tex]0[/tex] do [tex]2\pi[/tex] a r pustiš od [tex]0[/tex], do radijusa kružnice u kojoj se sijeku sfera i taj stožac, a to je upravo [tex]4a[/tex] (pošto radijus uopće ne ovisi o kutu). Jacobijan znaš i to je to.
[size=9][color=#999999]Added after 4 minutes:[/color][/size]
[/quote]
Prva jednadzba je sfera-kugla, a druga jednazdba ti nije stozac nego paraboloid okrenut prema dolje otvorom. Vrh mu je u 4a.
| fkirsek (napisa): | | mata (napisa): | A moze pliz pomoc oko 3. iz 2010./11.?  |
http://web.math.pmf.unizg.hr/nastava/difraf/int/2010-11/kolokvij1.pdf
Taj ti je najlakše u cilindričnim koordinatama. Primjeti, prva ploha je zapravo
[tex]x^2 + y^2 + (z - 2a)^2 = 4a[/tex], dakle sfera kojoj je središte točka [tex](0,0,2a)[/tex], a radijus [tex]2a[/tex].
Druga ploha je stožac okrenut prema gore. Za taj stožac su cilindrične koordinate posve prirodne, dobiješ jednadžbu:
[tex] az \leq 4a^2 - r^2[/tex], dok gornja jednadžba postaje:
[tex] (z-2a)^2 \leq 4a - r^2[/tex]
Dakle, granice od z-a izračunaš izravno iz tih jednadžbi, gornja je sfera, a donja je konus.
[tex]\phi[/tex] pustiš od [tex]0[/tex] do [tex]2\pi[/tex] a r pustiš od [tex]0[/tex], do radijusa kružnice u kojoj se sijeku sfera i taj stožac, a to je upravo [tex]4a[/tex] (pošto radijus uopće ne ovisi o kutu). Jacobijan znaš i to je to.
Added after 4 minutes:
|
Prva jednadzba je sfera-kugla, a druga jednazdba ti nije stozac nego paraboloid okrenut prema dolje otvorom. Vrh mu je u 4a.
|
|
| [Vrh] |
|
fkirsek
Forumaš(ica)

Pridružen/a: 28. 09. 2012. (23:52:51)
Postovi: (23)16
|
 Postano: 22:45 pon, 8. 4. 2013 Naslov: Postano: 22:45 pon, 8. 4. 2013 Naslov: |
    |
|
|
[quote="kiara"]Prva jednadzba je sfera-kugla, a druga jednazdba ti nije stozac nego paraboloid okrenut prema dolje otvorom. Vrh mu je u 4a.[/quote]
Istina, paraboloid je, no to ne utječe na rješenje.
[size=9][color=#999999]Added after 8 minutes:[/color][/size]
[quote="Pepper"]tako san i radila, al nisan sigurna za granice od r[/quote]
Ako gledaš ispravnu sliku, r bi ti trebao ići od [tex]4[/tex] do [tex]y+4[/tex] pošto te jednadžbe dobijaš kad uvrstiš tu supstituciju u jednadžbu.
| kiara (napisa): | | Prva jednadzba je sfera-kugla, a druga jednazdba ti nije stozac nego paraboloid okrenut prema dolje otvorom. Vrh mu je u 4a. |
Istina, paraboloid je, no to ne utječe na rješenje.
Added after 8 minutes:
| Pepper (napisa): | | tako san i radila, al nisan sigurna za granice od r |
Ako gledaš ispravnu sliku, r bi ti trebao ići od [tex]4[/tex] do [tex]y+4[/tex] pošto te jednadžbe dobijaš kad uvrstiš tu supstituciju u jednadžbu.
|
|
| [Vrh] |
|
matijaB
Forumaš(ica)

Pridružen/a: 19. 08. 2010. (09:11:43)
Postovi: (4D)16
|
|
| [Vrh] |
|
Nightrider
Forumaš s poteškoćama u pisanju


Pridružen/a: 19. 03. 2013. (19:01:05)
Postovi: (61)16
Spol: 
|
 Postano: 11:47 uto, 9. 4. 2013 Naslov: Postano: 11:47 uto, 9. 4. 2013 Naslov: |
    |
|
|
[quote="matijaB"][url]http://web.math.hr/nastava/difraf/int/2009-10/kolokvij1.pdf[/url]
jel zna ko 1. b) ono sa rotacijom spirale ?
Vec je odgovoreno par postova gore :D[/quote]
Odgovoreno je ali lose, bar je moj odgovor los jer sam prikazao parametrizaciju u nezgodnom obliku, ovako je jednostavnije:
Imas vezu izmedju polarnih i kartezijevih koordinata [latex]x=rcos \phi , y=rsin \phi[/latex] a jer je za spiralu [latex]r=\phi[/latex] dobijes parametarsku jednadzbu spirale:
[latex](x(\phi),y(\phi))=(\phi cos \phi , \phi sin \phi)[/latex] u intervalu [latex]\phi \in [0, \pi][/latex] i onda imas [url=http://en.wikipedia.org/wiki/Solid_of_revolution]ovdje[/url] formulu za volumen podrucja omedjenog krivuljom zadanom u parametarkom obliku koje rotira oko x-osi (cetvrta fomula od kraja):
Odgovoreno je ali lose, bar je moj odgovor los jer sam prikazao parametrizaciju u nezgodnom obliku, ovako je jednostavnije:
Imas vezu izmedju polarnih i kartezijevih koordinata 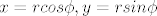 a jer je za spiralu a jer je za spiralu 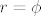 dobijes parametarsku jednadzbu spirale: dobijes parametarsku jednadzbu spirale:
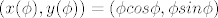 u intervalu u intervalu 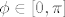 i onda imas ovdje formulu za volumen podrucja omedjenog krivuljom zadanom u parametarkom obliku koje rotira oko x-osi (cetvrta fomula od kraja): i onda imas ovdje formulu za volumen podrucja omedjenog krivuljom zadanom u parametarkom obliku koje rotira oko x-osi (cetvrta fomula od kraja):
Zadnja promjena: Nightrider; 16:30 uto, 9. 4. 2013; ukupno mijenjano 1 put.
|
|
| [Vrh] |
|
mamba
Forumaš(ica)

Pridružen/a: 09. 07. 2012. (17:11:16)
Postovi: (16)16
|
|
| [Vrh] |
|
pedro
Forumaš(ica)

Pridružen/a: 21. 10. 2010. (14:08:21)
Postovi: (19B)16
|
|
| [Vrh] |
|
mamba
Forumaš(ica)

Pridružen/a: 09. 07. 2012. (17:11:16)
Postovi: (16)16
|
|
| [Vrh] |
|
pedro
Forumaš(ica)

Pridružen/a: 21. 10. 2010. (14:08:21)
Postovi: (19B)16
|
|
| [Vrh] |
|
Ryssa
Forumaš(ica)


Pridružen/a: 18. 12. 2011. (00:10:28)
Postovi: (57)16
|
 Postano: 18:32 uto, 9. 4. 2013 Naslov: Postano: 18:32 uto, 9. 4. 2013 Naslov: |
    |
|
|
[quote="Nightrider"][quote="matijaB"][url]http://web.math.hr/nastava/difraf/int/2009-10/kolokvij1.pdf[/url]
jel zna ko 1. b) ono sa rotacijom spirale ?
Vec je odgovoreno par postova gore :D[/quote]
Odgovoreno je ali lose, bar je moj odgovor los jer sam prikazao parametrizaciju u nezgodnom obliku, ovako je jednostavnije:
Imas vezu izmedju polarnih i kartezijevih koordinata [latex]x=rcos \phi , y=rsin \phi[/latex] a jer je za spiralu [latex]r=\phi[/latex] dobijes parametarsku jednadzbu spirale:
[latex](x(\phi),y(\phi))=(\phi cos \phi , \phi sin \phi)[/latex] u intervalu [latex]\phi \in [0, \pi][/latex] i onda imas [url=http://en.wikipedia.org/wiki/Solid_of_revolution]ovdje[/url] formulu za volumen podrucja omedjenog krivuljom zadanom u parametarkom obliku koje rotira oko x-osi (cetvrta fomula od kraja):[/quote]
Ja sam to riješila na način da sam iskoristila formulu za područja prikazana polarnim koordinatama, dakle [tex]V=\frac{2}{3}\pi \int_{\varphi 1}^{\varphi 2} r^{3}\sin \varphi d\varphi [/tex]. U integralu sam samo stavila [tex]\varphi [/tex] umjesto r....neznam jesam li to uopće smjela napravit budući da ta formula vrijedi kada područje rotira oko polarne osi :S
| Nightrider (napisa): |
Odgovoreno je ali lose, bar je moj odgovor los jer sam prikazao parametrizaciju u nezgodnom obliku, ovako je jednostavnije:
Imas vezu izmedju polarnih i kartezijevih koordinata 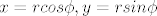 a jer je za spiralu a jer je za spiralu 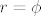 dobijes parametarsku jednadzbu spirale: dobijes parametarsku jednadzbu spirale:
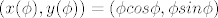 u intervalu u intervalu 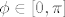 i onda imas ovdje formulu za volumen podrucja omedjenog krivuljom zadanom u parametarkom obliku koje rotira oko x-osi (cetvrta fomula od kraja): i onda imas ovdje formulu za volumen podrucja omedjenog krivuljom zadanom u parametarkom obliku koje rotira oko x-osi (cetvrta fomula od kraja): |
Ja sam to riješila na način da sam iskoristila formulu za područja prikazana polarnim koordinatama, dakle [tex]V=\frac{2}{3}\pi \int_{\varphi 1}^{\varphi 2} r^{3}\sin \varphi d\varphi [/tex]. U integralu sam samo stavila [tex]\varphi [/tex] umjesto r....neznam jesam li to uopće smjela napravit budući da ta formula vrijedi kada područje rotira oko polarne osi :S
|
|
| [Vrh] |
|
quark
Forumaš(ica)


Pridružen/a: 22. 10. 2011. (16:47:39)
Postovi: (DA)16
Spol: 
|
|
| [Vrh] |
|
Nightrider
Forumaš s poteškoćama u pisanju


Pridružen/a: 19. 03. 2013. (19:01:05)
Postovi: (61)16
Spol: 
|
 Postano: 20:00 uto, 9. 4. 2013 Naslov: Postano: 20:00 uto, 9. 4. 2013 Naslov: |
    |
|
|
[quote="Ryssa"]Ja sam to riješila na način da sam iskoristila formulu za područja prikazana polarnim koordinatama, dakle [tex]V=\frac{2}{3}\pi \int_{\varphi 1}^{\varphi 2} r^{3}\sin \varphi d\varphi [/tex]. U integralu sam samo stavila [tex]\varphi [/tex] umjesto r....neznam jesam li to uopće smjela napravit budući da ta formula vrijedi kada područje rotira oko polarne osi :S[/quote]
:D Nisam siguran, ja uglavnom biram parametarski prikaz no u ovom slucaju moj pristup sa parametarskim prikazom vodi do nezgodnog integrala dok tvoj pristup vodi do veoma zgodnog integrala. Mislim da si smjela jer, koliko ja znam, polarna os je os koja ide od pola(ishodista) prema nekom fiksnom smjeru definiranom kutem, ali ovdje je polarna os definirana ili kutem 0 ili kutem [latex]\pi[/latex] pa kako god uzmes polarna os se podudara sa x-osi, tako da je tvoj pristup dobar, puno bolji od moga.
[size=9][color=#999999]Added after 59 minutes:[/color][/size]
[quote="mamba"]
[quote="fkirsek"]
5. zadatak dakle.
a) Odgovor je DA! Naime, [tex]\bar{C}=C \cup \partial C[/tex]. Tj. rub skupa [tex]\bar{C}[/tex] je upravo [tex]\partial C[/tex].[/quote]
Može li pojašnjenje, zašto su im rubovi jednaki?[/quote]
Ne moraju rubovi od skupa C i zatvaraca skupa C biti jednaki no i ne treba ti pretpostavka da su ti rubovi jednaki da bi rijesio 5. a)
| Ryssa (napisa): | | Ja sam to riješila na način da sam iskoristila formulu za područja prikazana polarnim koordinatama, dakle [tex]V=\frac{2}{3}\pi \int_{\varphi 1}^{\varphi 2} r^{3}\sin \varphi d\varphi [/tex]. U integralu sam samo stavila [tex]\varphi [/tex] umjesto r....neznam jesam li to uopće smjela napravit budući da ta formula vrijedi kada područje rotira oko polarne osi :S |
 Nisam siguran, ja uglavnom biram parametarski prikaz no u ovom slucaju moj pristup sa parametarskim prikazom vodi do nezgodnog integrala dok tvoj pristup vodi do veoma zgodnog integrala. Mislim da si smjela jer, koliko ja znam, polarna os je os koja ide od pola(ishodista) prema nekom fiksnom smjeru definiranom kutem, ali ovdje je polarna os definirana ili kutem 0 ili kutem Nisam siguran, ja uglavnom biram parametarski prikaz no u ovom slucaju moj pristup sa parametarskim prikazom vodi do nezgodnog integrala dok tvoj pristup vodi do veoma zgodnog integrala. Mislim da si smjela jer, koliko ja znam, polarna os je os koja ide od pola(ishodista) prema nekom fiksnom smjeru definiranom kutem, ali ovdje je polarna os definirana ili kutem 0 ili kutem  pa kako god uzmes polarna os se podudara sa x-osi, tako da je tvoj pristup dobar, puno bolji od moga. pa kako god uzmes polarna os se podudara sa x-osi, tako da je tvoj pristup dobar, puno bolji od moga.
Added after 59 minutes:
| mamba (napisa): |
| fkirsek (napisa): |
5. zadatak dakle.
a) Odgovor je DA! Naime, [tex]\bar{C}=C \cup \partial C[/tex]. Tj. rub skupa [tex]\bar{C}[/tex] je upravo [tex]\partial C[/tex]. |
Može li pojašnjenje, zašto su im rubovi jednaki? |
Ne moraju rubovi od skupa C i zatvaraca skupa C biti jednaki no i ne treba ti pretpostavka da su ti rubovi jednaki da bi rijesio 5. a)
|
|
| [Vrh] |
|
matijaB
Forumaš(ica)

Pridružen/a: 19. 08. 2010. (09:11:43)
Postovi: (4D)16
|
|
| [Vrh] |
|
mamba
Forumaš(ica)

Pridružen/a: 09. 07. 2012. (17:11:16)
Postovi: (16)16
|
|
| [Vrh] |
|
quark
Forumaš(ica)


Pridružen/a: 22. 10. 2011. (16:47:39)
Postovi: (DA)16
Spol: 
|
|
| [Vrh] |
|
Nightrider
Forumaš s poteškoćama u pisanju


Pridružen/a: 19. 03. 2013. (19:01:05)
Postovi: (61)16
Spol: 
|
 Postano: 22:17 uto, 9. 4. 2013 Naslov: Postano: 22:17 uto, 9. 4. 2013 Naslov: |
    |
|
|
[quote="mamba"][quote="Nightrider"]
[quote="mamba"]
[quote="fkirsek"]
5. zadatak dakle.
a) Odgovor je DA! Naime, [tex]\bar{C}=C \cup \partial C[/tex]. Tj. rub skupa [tex]\bar{C}[/tex] je upravo [tex]\partial C[/tex].[/quote]
Može li pojašnjenje, zašto su im rubovi jednaki?[/quote]
Ne moraju rubovi od skupa C i zatvaraca skupa C biti jednaki no i ne treba ti pretpostavka da su ti rubovi jednaki da bi rijesio 5. a)[/quote]
A dobro, kako onda bez toga?[/quote]
Jednostavno.
fkirsek ti je rekao da ogranicen skup ima povrsinu ako i samo ako njegov rub ima povrsinu nula.
Oznacit cu zatvarac skupa C sa [latex]cl(C)[/latex]. Imamo po definiciji zatvaraca: [latex]cl(C)=C \cup \partial C[/latex]
Tada je [latex]P(cl(C))=P(C \cup \partial C)=P(C)+P(\partial C)=P(C)+0=P(C)[/latex] pa zatvarac skupa C ima povrsinu i ona je jednaka povrsini skupa C
[size=9][color=#999999]Added after 3 minutes:[/color][/size]
[quote="quark"]
Dovoljna je činjenica da je rub od zatvorenog C podskup ruba otvorenog C. Zato što za svaki podskup skupa koji je površine nule, vrijedi da je i on površine 0.[/quote]
Ovde je stavljen uvjet da je C ogranicen, nema spomena o njegovoj otvorenosti ili zatvorenosti.
| mamba (napisa): | | Nightrider (napisa): |
| mamba (napisa): |
| fkirsek (napisa): |
5. zadatak dakle.
a) Odgovor je DA! Naime, [tex]\bar{C}=C \cup \partial C[/tex]. Tj. rub skupa [tex]\bar{C}[/tex] je upravo [tex]\partial C[/tex]. |
Može li pojašnjenje, zašto su im rubovi jednaki? |
Ne moraju rubovi od skupa C i zatvaraca skupa C biti jednaki no i ne treba ti pretpostavka da su ti rubovi jednaki da bi rijesio 5. a) |
A dobro, kako onda bez toga? |
Jednostavno.
fkirsek ti je rekao da ogranicen skup ima povrsinu ako i samo ako njegov rub ima povrsinu nula.
Oznacit cu zatvarac skupa C sa 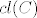 . Imamo po definiciji zatvaraca: . Imamo po definiciji zatvaraca: 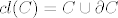
Tada je 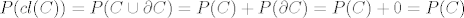 pa zatvarac skupa C ima povrsinu i ona je jednaka povrsini skupa C pa zatvarac skupa C ima povrsinu i ona je jednaka povrsini skupa C
Added after 3 minutes:
| quark (napisa): |
Dovoljna je činjenica da je rub od zatvorenog C podskup ruba otvorenog C. Zato što za svaki podskup skupa koji je površine nule, vrijedi da je i on površine 0. |
Ovde je stavljen uvjet da je C ogranicen, nema spomena o njegovoj otvorenosti ili zatvorenosti.
|
|
| [Vrh] |
|
|











