| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
Nightrider
Forumaš s poteškoćama u pisanju


Pridružen/a: 19. 03. 2013. (19:01:05)
Postovi: (61)16
Spol: 
|
 Postano: 20:34 pet, 5. 4. 2013 Naslov: Binomni koeficijenti Postano: 20:34 pet, 5. 4. 2013 Naslov: Binomni koeficijenti |
    |
|
|
Ja se mucim s ovim zadatkom vec nekih par dana i nikako da dodjem do rjesenja pa ako se netko zeli ukljuciti s idejama neka se osjeca slobodno da to ucini. A problem glasi ovako:
[i]Ima li jednadzba [latex]{n \choose m}=2{n-5 \choose m-5}[/latex] samo jedno rjesenje? Ako ima samo jedno dokazi da je to rjesenje jedino rjesenje,ako ima vise rjesenja pronadji jos jedno osim [latex](n,m)=(10,9)[/latex].[/i]
Ako se stavi [latex](n,m)=(10,9)[/latex] vidi se da je to rjesenje ali problem je dokazati da je to [b]jedino[/b] rjesenje (to je ono sto ja slutim, nisam u potpunosti iskljucio mogucnost drugog rjesenja ili vise rjesenja).
Ja sam uspio dovesti problem u neke ekvivalentne oblike ali to mi nije pomoglo da ga rijesim i mislim da je najbolje da ga ostavim u ovom svom jednostavnom obliku, mozda netko smisli neki jednostavan pristup problemu.
Edit: Bio sam stavio da zadatak glasi da se dokaze da ima samo jedno rjesenje no nije tako glasio u originalu vec je formulacija bliza u ovom obliku.
Ja se mucim s ovim zadatkom vec nekih par dana i nikako da dodjem do rjesenja pa ako se netko zeli ukljuciti s idejama neka se osjeca slobodno da to ucini. A problem glasi ovako:
Ima li jednadzba 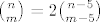 samo jedno rjesenje? Ako ima samo jedno dokazi da je to rjesenje jedino rjesenje,ako ima vise rjesenja pronadji jos jedno osim samo jedno rjesenje? Ako ima samo jedno dokazi da je to rjesenje jedino rjesenje,ako ima vise rjesenja pronadji jos jedno osim  . .
Ako se stavi  vidi se da je to rjesenje ali problem je dokazati da je to jedino rjesenje (to je ono sto ja slutim, nisam u potpunosti iskljucio mogucnost drugog rjesenja ili vise rjesenja). vidi se da je to rjesenje ali problem je dokazati da je to jedino rjesenje (to je ono sto ja slutim, nisam u potpunosti iskljucio mogucnost drugog rjesenja ili vise rjesenja).
Ja sam uspio dovesti problem u neke ekvivalentne oblike ali to mi nije pomoglo da ga rijesim i mislim da je najbolje da ga ostavim u ovom svom jednostavnom obliku, mozda netko smisli neki jednostavan pristup problemu.
Edit: Bio sam stavio da zadatak glasi da se dokaze da ima samo jedno rjesenje no nije tako glasio u originalu vec je formulacija bliza u ovom obliku.
Zadnja promjena: Nightrider; 12:19 sub, 6. 4. 2013; ukupno mijenjano 1 put.
|
|
| [Vrh] |
|
satja
Forumaš(ica)

Pridružen/a: 16. 05. 2010. (10:44:17)
Postovi: (F1)16
|
|
| [Vrh] |
|
Nightrider
Forumaš s poteškoćama u pisanju


Pridružen/a: 19. 03. 2013. (19:01:05)
Postovi: (61)16
Spol: 
|
|
| [Vrh] |
|
satja
Forumaš(ica)

Pridružen/a: 16. 05. 2010. (10:44:17)
Postovi: (F1)16
|
|
| [Vrh] |
|
Nightrider
Forumaš s poteškoćama u pisanju


Pridružen/a: 19. 03. 2013. (19:01:05)
Postovi: (61)16
Spol: 
|
|
| [Vrh] |
|
Nightrider
Forumaš s poteškoćama u pisanju


Pridružen/a: 19. 03. 2013. (19:01:05)
Postovi: (61)16
Spol: 
|
 Postano: 20:50 sri, 10. 4. 2013 Naslov: Postano: 20:50 sri, 10. 4. 2013 Naslov: |
    |
|
|
[quote="satja"][quote="Nightrider"]N={2,3,5,7,11,...} (prvo idu svi prosti brojevi pa onda ostali), u tom poretku skupa imamo [latex]\pi (n)=n[/latex] za svaki n iz N. [/quote]
Skup koji si naveo sadrzi samo proste brojeve pa stoga nije jednak skupu prirodnih brojeva. Radije stavi jedan prost, jedan slozen, jedan prost, jedan slozen i tako dalje.[/quote]
Ovo je iz one teme tamo, samo da ti kazem da nisi u pravu, moguce je konstruirat bijekciju sa N u N koja N transformira u skup S={2,3,5,7,...}={prvo idu svi prosti pa onda slozeni}, samo mi je trebalo malo vremena da ju konstruiram.
| satja (napisa): | | Nightrider (napisa): | N={2,3,5,7,11,...} (prvo idu svi prosti brojevi pa onda ostali), u tom poretku skupa imamo 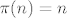 za svaki n iz N. za svaki n iz N. |
Skup koji si naveo sadrzi samo proste brojeve pa stoga nije jednak skupu prirodnih brojeva. Radije stavi jedan prost, jedan slozen, jedan prost, jedan slozen i tako dalje. |
Ovo je iz one teme tamo, samo da ti kazem da nisi u pravu, moguce je konstruirat bijekciju sa N u N koja N transformira u skup S={2,3,5,7,...}={prvo idu svi prosti pa onda slozeni}, samo mi je trebalo malo vremena da ju konstruiram.
|
|
| [Vrh] |
|
satja
Forumaš(ica)

Pridružen/a: 16. 05. 2010. (10:44:17)
Postovi: (F1)16
|
|
| [Vrh] |
|
Nightrider
Forumaš s poteškoćama u pisanju


Pridružen/a: 19. 03. 2013. (19:01:05)
Postovi: (61)16
Spol: 
|
|
| [Vrh] |
|
satja
Forumaš(ica)

Pridružen/a: 16. 05. 2010. (10:44:17)
Postovi: (F1)16
|
 Postano: 21:13 sri, 10. 4. 2013 Naslov: Postano: 21:13 sri, 10. 4. 2013 Naslov: |
    |
|
|
Naravno da ne postoji. Niz koji sadrži "prvo sve proste brojeve, pa onda složene" ogromna je besmislica. Npr., na kojoj se poziciji u tom nizu nalazi neki složeni broj, npr. broj 4? Očito ni na jednoj, jer je za svaku poziciju [tex]k[/tex] element [tex]a_k[/tex] prost, a ne složen. Sada čekam tvoj odgovor da shvatim trollaš li, ili si prethodni post zaista mislio ozbiljno. Koji god se od tih dvaju slučajeva pokazao točnim, pišeš gluposti i ubuduće na njih ne očekuj odgovore.
Naravno da ne postoji. Niz koji sadrži "prvo sve proste brojeve, pa onda složene" ogromna je besmislica. Npr., na kojoj se poziciji u tom nizu nalazi neki složeni broj, npr. broj 4? Očito ni na jednoj, jer je za svaku poziciju [tex]k[/tex] element [tex]a_k[/tex] prost, a ne složen. Sada čekam tvoj odgovor da shvatim trollaš li, ili si prethodni post zaista mislio ozbiljno. Koji god se od tih dvaju slučajeva pokazao točnim, pišeš gluposti i ubuduće na njih ne očekuj odgovore.
|
|
| [Vrh] |
|
Nightrider
Forumaš s poteškoćama u pisanju


Pridružen/a: 19. 03. 2013. (19:01:05)
Postovi: (61)16
Spol: 
|
|
| [Vrh] |
|
Borgcube
Forumaš(ica)
Pridružen/a: 01. 11. 2010. (21:14:10)
Postovi: (56)16
Lokacija: Tu i tamo.
|
 Postano: 21:43 sri, 10. 4. 2013 Naslov: Postano: 21:43 sri, 10. 4. 2013 Naslov: |
    |
|
|
Ajd prvo precizno definiraj što ti je zapravo
{prvo si prosti, a onda svi složeni}
Jel to skup? Ako je samo skup, onda je identičan kao [tex]\mathbb{N}[/tex]. Ako pričaš o totalno uređenom skupu, istina, možeš zaista konstruirati uređaj na skupu [tex]\mathbb{N}[/tex] u kojem će "ići prvo prosti, pa onda složeni".
Ali, onda ti je posve nebitno to što su ti baš prosti na početku, posve ti je nebitan taj uređaj da bi našao bijekciju s [tex]\mathbb{N}[/tex] u [tex]\mathbb{N}[/tex] (identiteta primjerice?) pošto nisi uopće mijenjao elemente skupa, samo si mijenjao poredak. Zaista postoji bijekcija između [tex]\mathbb{N}[/tex] i [tex]\mathbb{Z}[/tex], ali ne postoji sličnost; tj. na tu bijekciju ne utječe kako su ta dva skupa uređena.
Također, trivijalno se pokaže da takav TUS NIJE sličan kao TUS [tex](\mathbb{N}, <)[/tex]. Naime, za [tex](\mathbb{N}, <)[/tex] ne postoje beskonačni intervali dok u tvom TUS-u postoje.
Summa summarum:
ili si našao trivijalnu bijekciju između [tex]\mathbb{N}[/tex] i [tex]\mathbb{N}[/tex] (kao da nam takvih fali)
ili si napravio grešku.
Dakle ili trollaš ili... :)
Ajd prvo precizno definiraj što ti je zapravo
{prvo si prosti, a onda svi složeni}
Jel to skup? Ako je samo skup, onda je identičan kao [tex]\mathbb{N}[/tex]. Ako pričaš o totalno uređenom skupu, istina, možeš zaista konstruirati uređaj na skupu [tex]\mathbb{N}[/tex] u kojem će "ići prvo prosti, pa onda složeni".
Ali, onda ti je posve nebitno to što su ti baš prosti na početku, posve ti je nebitan taj uređaj da bi našao bijekciju s [tex]\mathbb{N}[/tex] u [tex]\mathbb{N}[/tex] (identiteta primjerice?) pošto nisi uopće mijenjao elemente skupa, samo si mijenjao poredak. Zaista postoji bijekcija između [tex]\mathbb{N}[/tex] i [tex]\mathbb{Z}[/tex], ali ne postoji sličnost; tj. na tu bijekciju ne utječe kako su ta dva skupa uređena.
Također, trivijalno se pokaže da takav TUS NIJE sličan kao TUS [tex](\mathbb{N}, <)[/tex]. Naime, za [tex](\mathbb{N}, <)[/tex] ne postoje beskonačni intervali dok u tvom TUS-u postoje.
Summa summarum:
ili si našao trivijalnu bijekciju između [tex]\mathbb{N}[/tex] i [tex]\mathbb{N}[/tex] (kao da nam takvih fali)
ili si napravio grešku.
Dakle ili trollaš ili... 
_________________
Ceterum censeo Carthaginem esse delendam.
|
|
| [Vrh] |
|
Nightrider
Forumaš s poteškoćama u pisanju


Pridružen/a: 19. 03. 2013. (19:01:05)
Postovi: (61)16
Spol: 
|
 Postano: 22:03 sri, 10. 4. 2013 Naslov: Postano: 22:03 sri, 10. 4. 2013 Naslov: |
    |
|
|
[quote="Borgcube"]Ajd prvo precizno definiraj što ti je zapravo
{prvo svi prosti, a onda svi složeni} [/quote]
U tome i lezi problem. Ako se napise S={prvo svi prosti, a onda svi slozeni} onda stvarno primjedba: "u tom skupu nema slozenih brojeva" ima nekog smisla, jer ako oznacimo sa a_k k-ti element skupa S onda bi bilo a_k je prost za svaki k iz N.
No ta bijekcija upravo to napravi, ona skup N transformira u skup S={prvo svi prosti, a onda svi slozeni}.
[quote="Borgcube"]Dakle ili trollaš ili... :)[/quote]
Ili?
| Borgcube (napisa): | Ajd prvo precizno definiraj što ti je zapravo
{prvo svi prosti, a onda svi složeni} |
U tome i lezi problem. Ako se napise S={prvo svi prosti, a onda svi slozeni} onda stvarno primjedba: "u tom skupu nema slozenih brojeva" ima nekog smisla, jer ako oznacimo sa a_k k-ti element skupa S onda bi bilo a_k je prost za svaki k iz N.
No ta bijekcija upravo to napravi, ona skup N transformira u skup S={prvo svi prosti, a onda svi slozeni}.
| Borgcube (napisa): | Dakle ili trollaš ili...  |
Ili?
|
|
| [Vrh] |
|
Borgcube
Forumaš(ica)
Pridružen/a: 01. 11. 2010. (21:14:10)
Postovi: (56)16
Lokacija: Tu i tamo.
|
|
| [Vrh] |
|
Nightrider
Forumaš s poteškoćama u pisanju


Pridružen/a: 19. 03. 2013. (19:01:05)
Postovi: (61)16
Spol: 
|
|
| [Vrh] |
|
vsego
Site Admin


Pridružen/a: 06. 10. 2002. (22:07:09)
Postovi: (3562)16
Spol: 
Lokacija: /sbin/init
|
 Postano: 23:11 sri, 10. 4. 2013 Naslov: Postano: 23:11 sri, 10. 4. 2013 Naslov: |
    |
|
|
[color=darkred]Pošto ti je kolega lijepo objasnio zašto takva bijekcija ne postoji, tj. zašto tvoj skup nije jednak skupu svih prirodnih brojeva, i još ti je postavio pitanje na koje nisi odgovorio ("na kojoj se poziciji u tom nizu nalazi neki složeni broj, npr. broj 4?"), slazem se s njegovom procjenom da trollaš. Ako i nije tako, to i dalje ne opravdava nastup "ja sam u pravu iako mi dokazujete da nisam, a ja ne znam (protu)argumentirati da jesam". Tvrdoglavljenju bez argumenata nije mjesto u matematici, nego u nekim drugim područjima ljudskih aktivnosti.
Zato te sada lijepo molim da prestaneš. Nisam baš strpljiv čovjek pa ću se ograničiti na samo jednu lijepu molbu.
Kolege, ubuduće ako mislite da je netko troll, nemojte ga hraniti, pa će ga glad odvesti negdje drugdje.[/color] ;)
:lockdance:
Pošto ti je kolega lijepo objasnio zašto takva bijekcija ne postoji, tj. zašto tvoj skup nije jednak skupu svih prirodnih brojeva, i još ti je postavio pitanje na koje nisi odgovorio ("na kojoj se poziciji u tom nizu nalazi neki složeni broj, npr. broj 4?"), slazem se s njegovom procjenom da trollaš. Ako i nije tako, to i dalje ne opravdava nastup "ja sam u pravu iako mi dokazujete da nisam, a ja ne znam (protu)argumentirati da jesam". Tvrdoglavljenju bez argumenata nije mjesto u matematici, nego u nekim drugim područjima ljudskih aktivnosti.
Zato te sada lijepo molim da prestaneš. Nisam baš strpljiv čovjek pa ću se ograničiti na samo jednu lijepu molbu.
Kolege, ubuduće ako mislite da je netko troll, nemojte ga hraniti, pa će ga glad odvesti negdje drugdje. 

_________________ U pravilu ignoriram pitanja u krivim topicima i kodove koji nisu u [code]...[/code] blokovima.
Takodjer, OBJASNITE sto vas muci! "Sto mi je krivo?", bez opisa u cemu je problem, rijetko ce zadobiti moju paznju.  |
|
| [Vrh] |
|
|












