| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
dodinho
Forumaš(ica)
Pridružen/a: 27. 09. 2011. (11:17:47)
Postovi: (4B)16
|
|
| [Vrh] |
|
dodinho
Forumaš(ica)
Pridružen/a: 27. 09. 2011. (11:17:47)
Postovi: (4B)16
|
|
| [Vrh] |
|
Lafiel
Forumaš(ica)


Pridružen/a: 26. 09. 2007. (09:56:59)
Postovi: (153)16
Spol: 
|
|
| [Vrh] |
|
dodinho
Forumaš(ica)
Pridružen/a: 27. 09. 2011. (11:17:47)
Postovi: (4B)16
|
|
| [Vrh] |
|
Lafiel
Forumaš(ica)


Pridružen/a: 26. 09. 2007. (09:56:59)
Postovi: (153)16
Spol: 
|
|
| [Vrh] |
|
Phoenix
Forumaš(ica)


Pridružen/a: 15. 05. 2010. (18:46:07)
Postovi: (164)16
Sarma: -
|
 Postano: 21:27 sri, 10. 4. 2013 Naslov: Postano: 21:27 sri, 10. 4. 2013 Naslov: |
    |
|
|
dodinho, suosjećam s tobom i znam kako ti je, pa ću ti potvrditi da su ti oba odgovora točna. :)
Za prvi zadatak, [tex]\left\{ |f| < +\infty \right\} \in \mathcal{F}[/tex], možeš shvatiti da, ako je [tex]|f(x)| < +\infty[/tex] za neki [tex]x \in X[/tex], sigurno postoji [tex]n \in \mathbb{N}[/tex] takav da je [tex]|f(x)|<n[/tex] (Arhimedov aksiom, ako ćeš formalno), odnosno [tex]-n<f(x)<n[/tex]. Tada je [tex]x \in \left\{ f>-n \right\}[/tex] i [tex]x \in \left\{ f<n \right\}[/tex], pa svakako i u obe unije koje si raspisao i konačno u onom presjeku.
Obratno za [tex]x[/tex] iz tvog presjeka slijedi da pripada objema unijama, a to znači da postoje [tex]n,m \in \mathbb{N}[/tex] takvi da je [tex]-m<f(x)<n[/tex], a to povlači [tex]|f(x)|<+\infty[/tex].
Ukratko, skup od kojeg si krenuo jednak je onom do kojeg si došao - sada si siguran da ti skupovna jednakost vrijedi.
Time je pokrivena intuicija! Dalje, vidim, znaš objasniti i riješiti zadatak... :)
A ovo drugo ti je dobro iz razloga što je [tex]\displaystyle \mathrm{sup} f_n \geq f_n[/tex], odnosno [tex]\left( \mathrm{sup} f_n\right) (x) \geq f_k(x), \forall x \in X[/tex] i [tex]\forall k \in \mathbb{N}[/tex] (inače bih napisao [tex]n[/tex] umjesto [tex]k[/tex], no onda miješam dvije različite oznake). Stoga, ako jest [tex]f_n \geq \alpha[/tex] za neki [tex]n[/tex], svakako je i [tex]\mathrm{sup} f_n \geq \alpha[/tex].
Lafiel, u pravu si s tim da ne mora vrijediti [tex]f_n \geq \alpha[/tex] za svaki [tex]n[/tex], no baš zato i stoji unija - mora barem neka funkcija [tex]f_n[/tex] iz tog niza na cijeloj svojoj domeni [tex]X[/tex] biti veća ili jednaka [tex]\alpha[/tex] pa će zato i [tex]\sup f_n[/tex] biti veći ili jednak [tex]\alpha[/tex]. :)
dodinho, suosjećam s tobom i znam kako ti je, pa ću ti potvrditi da su ti oba odgovora točna. 
Za prvi zadatak, [tex]\left\{ |f| < +\infty \right\} \in \mathcal{F}[/tex], možeš shvatiti da, ako je [tex]|f(x)| < +\infty[/tex] za neki [tex]x \in X[/tex], sigurno postoji [tex]n \in \mathbb{N}[/tex] takav da je [tex]|f(x)|<n[/tex] (Arhimedov aksiom, ako ćeš formalno), odnosno [tex]-n<f(x)<n[/tex]. Tada je [tex]x \in \left\{ f>-n \right\}[/tex] i [tex]x \in \left\{ f<n \right\}[/tex], pa svakako i u obe unije koje si raspisao i konačno u onom presjeku.
Obratno za [tex]x[/tex] iz tvog presjeka slijedi da pripada objema unijama, a to znači da postoje [tex]n,m \in \mathbb{N}[/tex] takvi da je [tex]-m<f(x)<n[/tex], a to povlači [tex]|f(x)|<+\infty[/tex].
Ukratko, skup od kojeg si krenuo jednak je onom do kojeg si došao - sada si siguran da ti skupovna jednakost vrijedi.
Time je pokrivena intuicija! Dalje, vidim, znaš objasniti i riješiti zadatak... 
A ovo drugo ti je dobro iz razloga što je [tex]\displaystyle \mathrm{sup} f_n \geq f_n[/tex], odnosno [tex]\left( \mathrm{sup} f_n\right) (x) \geq f_k(x), \forall x \in X[/tex] i [tex]\forall k \in \mathbb{N}[/tex] (inače bih napisao [tex]n[/tex] umjesto [tex]k[/tex], no onda miješam dvije različite oznake). Stoga, ako jest [tex]f_n \geq \alpha[/tex] za neki [tex]n[/tex], svakako je i [tex]\mathrm{sup} f_n \geq \alpha[/tex].
Lafiel, u pravu si s tim da ne mora vrijediti [tex]f_n \geq \alpha[/tex] za svaki [tex]n[/tex], no baš zato i stoji unija - mora barem neka funkcija [tex]f_n[/tex] iz tog niza na cijeloj svojoj domeni [tex]X[/tex] biti veća ili jednaka [tex]\alpha[/tex] pa će zato i [tex]\sup f_n[/tex] biti veći ili jednak [tex]\alpha[/tex]. 
|
|
| [Vrh] |
|
dodinho
Forumaš(ica)
Pridružen/a: 27. 09. 2011. (11:17:47)
Postovi: (4B)16
|
|
| [Vrh] |
|
Lafiel
Forumaš(ica)


Pridružen/a: 26. 09. 2007. (09:56:59)
Postovi: (153)16
Spol: 
|
|
| [Vrh] |
|
dodinho
Forumaš(ica)
Pridružen/a: 27. 09. 2011. (11:17:47)
Postovi: (4B)16
|
|
| [Vrh] |
|
dodinho
Forumaš(ica)
Pridružen/a: 27. 09. 2011. (11:17:47)
Postovi: (4B)16
|
|
| [Vrh] |
|
Gost
|
 Postano: 13:13 čet, 11. 4. 2013 Naslov: Postano: 13:13 čet, 11. 4. 2013 Naslov: |
    |
|
|
Pogledaj definiciju vanjske mjere, (3.9) u skripti iz predavanja.
Sada vidimo da cijeli R pokriva bilokoji neprebrojivi skup, npr. S.
μ(R) = 1 jer mu je komplement, prazan skup, prebrojiv. Sada lako slijedi da je μ*(S) = 1, jer μ*(S) = infimum skupa koji sadrzi brojeve vece ili jednake 1, a ne mozes sadrzavati nulu jer bi onda neprebrojiv S prekrivala prebrojiva unija prebrojivih skupova koja je prebrojiv skup.
Dakle za svaki neprebrojiv skup S je μ*(S) = 1.
Pogledaj definiciju vanjske mjere, (3.9) u skripti iz predavanja.
Sada vidimo da cijeli R pokriva bilokoji neprebrojivi skup, npr. S.
μ(R) = 1 jer mu je komplement, prazan skup, prebrojiv. Sada lako slijedi da je μ*(S) = 1, jer μ*(S) = infimum skupa koji sadrzi brojeve vece ili jednake 1, a ne mozes sadrzavati nulu jer bi onda neprebrojiv S prekrivala prebrojiva unija prebrojivih skupova koja je prebrojiv skup.
Dakle za svaki neprebrojiv skup S je μ*(S) = 1.
|
|
| [Vrh] |
|
dodinho
Forumaš(ica)
Pridružen/a: 27. 09. 2011. (11:17:47)
Postovi: (4B)16
|
|
| [Vrh] |
|
Gost
|
 Postano: 16:00 čet, 11. 4. 2013 Naslov: Postano: 16:00 čet, 11. 4. 2013 Naslov: |
    |
|
|
[quote="dodinho"]Hvala na odgovoru. Nemam neki poseban razlog vec zelim da mi netko potvrdi da znam sigurno da sam na dobrom putu razmisljanja :wink:
[size=9][color=#999999]Added after 11 minutes:[/color][/size]
http://web.math.pmf.unizg.hr/nastava/mii/files/Izmjerive_funkcije_07.pdf
Zad.82. : Na vjezbama je ponudjeno rjesenje izmjerivosti od sup fn (n je ovdje indeks, tj. supskript kao u zadatku) na sljedeci nacin :
{ sup fn ≤ α } = ∩{ fn ≤ α } ∈ F, pri cemu ∩ : n ide od 1 do ∞ .
Ovo je moja verzija : { sup fn ≥ α } = U{ fn ≥ α } ∈ F. Naravno, U ide isto od 1 do ∞.
Mozda je opet banalno, ali me zanima tvoje misljenje ili vec tko bude citao.
Tnx :naklon:[/quote]
Mislim da mora biti stroga nejednakost da bi jednakost skupova vrijedila:
{ sup fn > α } = U{ fn > α }
Protuprimjer za kad je >= bi bio:
fn(x) := x(2 - 1/n), definirano na x > 0
=> sup fn(x) = 2x
Sada su skupovi, za npr α = 2;
{ sup fn >= 2 } = { 2x >= 2 } = { x >= 1 }
U{ fn >= 2 } = U{ x(2 - 1/n) >= 2 } = U{ x >= 1/(1 - 1/2n) } = { x > 1 }
Pa su razliciti.
| dodinho (napisa): | Hvala na odgovoru. Nemam neki poseban razlog vec zelim da mi netko potvrdi da znam sigurno da sam na dobrom putu razmisljanja 
Added after 11 minutes:
http://web.math.pmf.unizg.hr/nastava/mii/files/Izmjerive_funkcije_07.pdf
Zad.82. : Na vjezbama je ponudjeno rjesenje izmjerivosti od sup fn (n je ovdje indeks, tj. supskript kao u zadatku) na sljedeci nacin :
{ sup fn ≤ α } = ∩{ fn ≤ α } ∈ F, pri cemu ∩ : n ide od 1 do ∞ .
Ovo je moja verzija : { sup fn ≥ α } = U{ fn ≥ α } ∈ F. Naravno, U ide isto od 1 do ∞.
Mozda je opet banalno, ali me zanima tvoje misljenje ili vec tko bude citao.
Tnx  |
Mislim da mora biti stroga nejednakost da bi jednakost skupova vrijedila:
{ sup fn > α } = U{ fn > α }
Protuprimjer za kad je >= bi bio:
fn(x) := x(2 - 1/n), definirano na x > 0
⇒ sup fn(x) = 2x
Sada su skupovi, za npr α = 2;
{ sup fn >= 2 } = { 2x >= 2 } = { x >= 1 }
U{ fn >= 2 } = U{ x(2 - 1/n) >= 2 } = U{ x >= 1/(1 - 1/2n) } = { x > 1 }
Pa su razliciti.
|
|
| [Vrh] |
|
dodinho
Forumaš(ica)
Pridružen/a: 27. 09. 2011. (11:17:47)
Postovi: (4B)16
|
|
| [Vrh] |
|
Lafiel
Forumaš(ica)


Pridružen/a: 26. 09. 2007. (09:56:59)
Postovi: (153)16
Spol: 
|
 Postano: 17:53 čet, 11. 4. 2013 Naslov: Postano: 17:53 čet, 11. 4. 2013 Naslov: |
    |
|
|
Trebam pomoć sa četvrtim zadatkom iz [url=http://web.math.pmf.unizg.hr/nastava/mii/files/mii-kol1-2012-rj.pdf]prošlogodišnjeg kolokvija[/url]:
[latex]\mathcal{C} := \{< -\infty, b] : b \in \mathbb{R}\}[/latex]
[latex]\mathcal{F} := \{B \in \mathcal{B}(\mathbb{R}) : \mu(A)\mu(B) = \mu(\mathbb{R})\mu(A\cap B)\}[/latex]
Zašto se uvjet zadatka može formulirati kao [tex] \mathcal{C}\subseteq \mathcal{F}[/tex]?
I u alternativnom rješenju istog zadatka, tekst rješenja je
[quote]Prema uvjetu zadatka je [tex]\mu_{1}(< -\infty, b]) = \mu_{2}(< -\infty, b])[/tex] za svaki [tex]b \in \mathbb{R}[/tex], odakle oduzimanjem odmah slijedi i [tex]\mu_{1}(<a, b]) = \mu_{2}(<a, b])[/tex], za svake [tex]a, b \in \mathbb{R}, a < b[/tex]. Zato su [tex]\mu_{1}[/tex] i [tex]\mu_{2}[/tex] dvije Lebesgue-Stieltjesove mjere pridružene istoj rastućoj zdesna neprekidnoj funkciji...[/quote]
Možda glupo pitanje, ali oduzimanjem čega? I kako onda iz toga zaključujemo da su to baš Lebesgue-Stieltjesove mjere? :oops:
Trebam pomoć sa četvrtim zadatkom iz prošlogodišnjeg kolokvija:
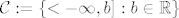
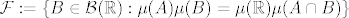
Zašto se uvjet zadatka može formulirati kao [tex] \mathcal{C}\subseteq \mathcal{F}[/tex]?
I u alternativnom rješenju istog zadatka, tekst rješenja je
| Citat: | | Prema uvjetu zadatka je [tex]\mu_{1}(< -\infty, b]) = \mu_{2}(< -\infty, b])[/tex] za svaki [tex]b \in \mathbb{R}[/tex], odakle oduzimanjem odmah slijedi i [tex]\mu_{1}(<a, b]) = \mu_{2}(<a, b])[/tex], za svake [tex]a, b \in \mathbb{R}, a < b[/tex]. Zato su [tex]\mu_{1}[/tex] i [tex]\mu_{2}[/tex] dvije Lebesgue-Stieltjesove mjere pridružene istoj rastućoj zdesna neprekidnoj funkciji... |
Možda glupo pitanje, ali oduzimanjem čega? I kako onda iz toga zaključujemo da su to baš Lebesgue-Stieltjesove mjere? 
_________________
Weit von hier fällt Gold von den Sternen
|
|
| [Vrh] |
|
Phoenix
Forumaš(ica)


Pridružen/a: 15. 05. 2010. (18:46:07)
Postovi: (164)16
Sarma: -
|
 Postano: 18:58 čet, 11. 4. 2013 Naslov: Postano: 18:58 čet, 11. 4. 2013 Naslov: |
    |
|
|
Kolegi Gostu hvala na ispravku, a kolegi dodinhu iskrene isprike na krivom rješenju!
Lafiel: Pri uvjetu zadatka se misli da jednakost zapisana u [tex]\mathcal{F}[/tex] vrijedi za sve intervale oblika [tex]\left< -\infty, b \right][/tex], a to su upravo elementi skupa [tex]\mathcal{C}[/tex]. Odnosno, u iskazu zadatka eksplicitno piše kako jednakost vrijedi za dane poluotvorene intervale, a, za potrebe rješenja zadatka, to je prikazano kao [tex]\mathcal{C} \subseteq \mathcal{F}[/tex] (što, kad doslovno čitamo, znači: ako je skup poluotvoren interval, zadovoljava jednakost.)
Za alternativno rješenje: oduzimanjem [tex]\mu_1 \left( \left< -\infty, b \right] \right) - \mu_1 \left( \left< -\infty, a \right] \right)[/tex], odnosno [tex]\mu_2 \left( \left< -\infty, b \right] \right) - \mu_2 \left( \left< -\infty, a \right] \right)[/tex]. Oduzimanje je dozvoljeno jer su vrijednosti koje oduzimamo konačne (odnosno, nisu jednake [tex]+\infty[/tex], što slijedi iz činjenice da su mjere vjerojatnosne), a konačnu jednakost dobivamo jer je drugi interval podskup prvog za [tex]a<b[/tex], pa se razlika mjera skupova svodi na mjeru skupovne razlike - što je [tex]\left< a,b \right][/tex].
Pitaj ako ti nisam dovoljno dobro raspisao jer sam napisao samo kratke natuknice - raspisat ću i više ovisno o tvojoj potrebi. :)
Kolegi Gostu hvala na ispravku, a kolegi dodinhu iskrene isprike na krivom rješenju!
Lafiel: Pri uvjetu zadatka se misli da jednakost zapisana u [tex]\mathcal{F}[/tex] vrijedi za sve intervale oblika [tex]\left< -\infty, b \right][/tex], a to su upravo elementi skupa [tex]\mathcal{C}[/tex]. Odnosno, u iskazu zadatka eksplicitno piše kako jednakost vrijedi za dane poluotvorene intervale, a, za potrebe rješenja zadatka, to je prikazano kao [tex]\mathcal{C} \subseteq \mathcal{F}[/tex] (što, kad doslovno čitamo, znači: ako je skup poluotvoren interval, zadovoljava jednakost.)
Za alternativno rješenje: oduzimanjem [tex]\mu_1 \left( \left< -\infty, b \right] \right) - \mu_1 \left( \left< -\infty, a \right] \right)[/tex], odnosno [tex]\mu_2 \left( \left< -\infty, b \right] \right) - \mu_2 \left( \left< -\infty, a \right] \right)[/tex]. Oduzimanje je dozvoljeno jer su vrijednosti koje oduzimamo konačne (odnosno, nisu jednake [tex]+\infty[/tex], što slijedi iz činjenice da su mjere vjerojatnosne), a konačnu jednakost dobivamo jer je drugi interval podskup prvog za [tex]a<b[/tex], pa se razlika mjera skupova svodi na mjeru skupovne razlike - što je [tex]\left< a,b \right][/tex].
Pitaj ako ti nisam dovoljno dobro raspisao jer sam napisao samo kratke natuknice - raspisat ću i više ovisno o tvojoj potrebi. 
|
|
| [Vrh] |
|
dodinho
Forumaš(ica)
Pridružen/a: 27. 09. 2011. (11:17:47)
Postovi: (4B)16
|
 Postano: 19:10 čet, 11. 4. 2013 Naslov: Postano: 19:10 čet, 11. 4. 2013 Naslov: |
    |
|
|
[quote="Lafiel"]Trebam pomoć sa četvrtim zadatkom iz [url=http://web.math.pmf.unizg.hr/nastava/mii/files/mii-kol1-2012-rj.pdf]prošlogodišnjeg kolokvija[/url]:
[latex]\mathcal{C} := \{< -\infty, b] : b \in \mathbb{R}\}[/latex]
[latex]\mathcal{F} := \{B \in \mathcal{B}(\mathbb{R}) : \mu(A)\mu(B) = \mu(\mathbb{R})\mu(A\cap B)\}[/latex]
Zašto se uvjet zadatka može formulirati kao [tex] \mathcal{C}\subseteq \mathcal{F}[/tex]?
[/quote]
Neka je A ∈ B([b]R[/b]) .
U [b]F[/b] se nalaze svi B ∈ B([b]R[/b]) za koje vrijedi μ(A)μ(B)=μ([b]R[/b])μ(A∩B) pa se tako posebno nalaze i < -∞,b] ∈ B([b]R[/b]), za svaki b ∈ [b]R[/b] , jer je tako zadano u zadatku.
S obzirom da je < -∞,b] ∈ [b]C[/b], za svaki b ∈ [b]R[/b], slijedi da je [b]C[/b] ⊆ [b]F[/b]
[size=9][color=#999999]Added after 1 minutes:[/color][/size]
Eto, gore sve pise... :wink:
| Lafiel (napisa): | Trebam pomoć sa četvrtim zadatkom iz prošlogodišnjeg kolokvija:
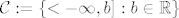
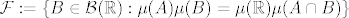
Zašto se uvjet zadatka može formulirati kao [tex] \mathcal{C}\subseteq \mathcal{F}[/tex]?
|
Neka je A ∈ B(R) .
U F se nalaze svi B ∈ B(R) za koje vrijedi μ(A)μ(B)=μ(R)μ(A∩B) pa se tako posebno nalaze i < -∞,b] ∈ B(R), za svaki b ∈ R , jer je tako zadano u zadatku.
S obzirom da je < -∞,b] ∈ C, za svaki b ∈ R, slijedi da je C ⊆ F
Added after 1 minutes:
Eto, gore sve pise... 
|
|
| [Vrh] |
|
Lafiel
Forumaš(ica)


Pridružen/a: 26. 09. 2007. (09:56:59)
Postovi: (153)16
Spol: 
|
 Postano: 20:06 čet, 11. 4. 2013 Naslov: Postano: 20:06 čet, 11. 4. 2013 Naslov: |
    |
|
|
O bože budale, ja sam pod "uvjet zadatka" cijelo vrijeme mislila na [tex]\mu(A) = 0[/tex] ili [tex]\mu(A^c) = 0[/tex] pa mi zato nikako nije bilo jasno kakve to veze ima s bilo čime. Ovako to ipak ima smisla. :zubo: Hvala obojici.
[quote="Phoenix"]Za alternativno rješenje: oduzimanjem [tex]\mu_1 \left( \left< -\infty, b \right] \right) - \mu_1 \left( \left< -\infty, a \right] \right)[/tex], odnosno [tex]\mu_2 \left( \left< -\infty, b \right] \right) - \mu_2 \left( \left< -\infty, a \right] \right)[/tex]. Oduzimanje je dozvoljeno jer su vrijednosti koje oduzimamo konačne (odnosno, nisu jednake [tex]+\infty[/tex], što slijedi iz činjenice da su mjere vjerojatnosne), a konačnu jednakost dobivamo jer je drugi interval podskup prvog za [tex]a<b[/tex], pa se razlika mjera skupova svodi na mjeru skupovne razlike - što je [tex]\left< a,b \right][/tex].[/quote]
Aaah, OK, sad mi je jasno što se tiče oduzimanja. A odakle zaključak da su one baš Lebesgue-Stieltjesove mjere?
O bože budale, ja sam pod "uvjet zadatka" cijelo vrijeme mislila na [tex]\mu(A) = 0[/tex] ili [tex]\mu(A^c) = 0[/tex] pa mi zato nikako nije bilo jasno kakve to veze ima s bilo čime. Ovako to ipak ima smisla.  Hvala obojici. Hvala obojici.
| Phoenix (napisa): | | Za alternativno rješenje: oduzimanjem [tex]\mu_1 \left( \left< -\infty, b \right] \right) - \mu_1 \left( \left< -\infty, a \right] \right)[/tex], odnosno [tex]\mu_2 \left( \left< -\infty, b \right] \right) - \mu_2 \left( \left< -\infty, a \right] \right)[/tex]. Oduzimanje je dozvoljeno jer su vrijednosti koje oduzimamo konačne (odnosno, nisu jednake [tex]+\infty[/tex], što slijedi iz činjenice da su mjere vjerojatnosne), a konačnu jednakost dobivamo jer je drugi interval podskup prvog za [tex]a<b[/tex], pa se razlika mjera skupova svodi na mjeru skupovne razlike - što je [tex]\left< a,b \right][/tex]. |
Aaah, OK, sad mi je jasno što se tiče oduzimanja. A odakle zaključak da su one baš Lebesgue-Stieltjesove mjere?
_________________
Weit von hier fällt Gold von den Sternen
|
|
| [Vrh] |
|
kosani
Forumaš(ica)
Pridružen/a: 14. 11. 2010. (21:22:58)
Postovi: (26)16
|
|
| [Vrh] |
|
Phoenix
Forumaš(ica)


Pridružen/a: 15. 05. 2010. (18:46:07)
Postovi: (164)16
Sarma: -
|
 Postano: 20:21 čet, 11. 4. 2013 Naslov: Postano: 20:21 čet, 11. 4. 2013 Naslov: |
    |
|
|
Prije teorema [tex]4. 19[/tex] se danoj mjeri (koja je konačna za svaki kompaktan skup za koji je definirana!) pridružuje određena funkcija s prva dva opisana svojstva, tj. prve dvije točke (neopadajuća i neprekidna zdesna), dok se kroz napomenu [tex]4. 21[/tex] predočava klasa funkcija koja zadovoljava oba svojstva i pripisuje se određenoj mjeri. Kao što napomena kaže, do jedinstvenosti dolazimo svojstvom poput, dogovorno, svojstva pod trećom točkom.
Po definiciji pripadne funkcije u [tex]\left( 4. 18 \right)[/tex] dobivamo podudarnost funkcija distribucija za obe mjere u zadatku (zajedno sa svojstvom da su u nuli jednake nula), a zatim iz teorema [tex]4. 19[/tex] jednakost tih mjera (kako postoji jedinstvena Lebesgue-Stieltjesova mjera za danu funkciju).
Ukratko, ključno je bilo da se mjere podudaraju na opisanim poluintervalima.
(No, tada si mogla, recimo, iskoristiti korolar [tex]4.6[/tex] umjesto ovoga i rješenje bi opet bilo dobro. :))
kosani,
[tex]E \in \mathcal{R}[/tex] pa je posebno i u strukturi generiranoj tim skupom (odnosno, vrijedi [tex]\mathcal{R} \subseteq \mathcal{M} \left( \mathcal{R} \right)[/tex]).
Za [tex]\mu \left( \emptyset \right)[/tex], vjerujem da se tada gleda [tex]\emptyset[/tex] kao [tex]\left< a,a \right] \times \left< a,a \right][/tex] za bilo koji [tex]a \in \mathbb{R}[/tex]. Tako smo na vježbama spominjali kada smo obrađivali prvu točku primjera [tex]2.9[/tex], a poklapa se i s definicijom [tex]d[/tex]-intervala u primjeru [tex]2.2[/tex] [tex](b)[/tex].
Uglavnom, da, takav dogovor narušava bitno svojstvo da prazan skup ide u nulu (dapače, slika funkcije postaje pravi nadskup od [tex]\left[ 0, +\infty \right][/tex]); no, mislim da se ipak referencira na ovo što navodim pošto je taj dogovor ipak uveden kasnije i uz nešto drugačije područje ovog kolegija.
(A ako misliš da definicija koju ti zadaš nije dovoljno jasna ili precizna, uvijek je dobro napomenuti kako se definicija točno ponaša za prazan skup ili pak njega posebno preslikati u nulu.)
Prije teorema [tex]4. 19[/tex] se danoj mjeri (koja je konačna za svaki kompaktan skup za koji je definirana!) pridružuje određena funkcija s prva dva opisana svojstva, tj. prve dvije točke (neopadajuća i neprekidna zdesna), dok se kroz napomenu [tex]4. 21[/tex] predočava klasa funkcija koja zadovoljava oba svojstva i pripisuje se određenoj mjeri. Kao što napomena kaže, do jedinstvenosti dolazimo svojstvom poput, dogovorno, svojstva pod trećom točkom.
Po definiciji pripadne funkcije u [tex]\left( 4. 18 \right)[/tex] dobivamo podudarnost funkcija distribucija za obe mjere u zadatku (zajedno sa svojstvom da su u nuli jednake nula), a zatim iz teorema [tex]4. 19[/tex] jednakost tih mjera (kako postoji jedinstvena Lebesgue-Stieltjesova mjera za danu funkciju).
Ukratko, ključno je bilo da se mjere podudaraju na opisanim poluintervalima.
(No, tada si mogla, recimo, iskoristiti korolar [tex]4.6[/tex] umjesto ovoga i rješenje bi opet bilo dobro.  ) )
kosani,
[tex]E \in \mathcal{R}[/tex] pa je posebno i u strukturi generiranoj tim skupom (odnosno, vrijedi [tex]\mathcal{R} \subseteq \mathcal{M} \left( \mathcal{R} \right)[/tex]).
Za [tex]\mu \left( \emptyset \right)[/tex], vjerujem da se tada gleda [tex]\emptyset[/tex] kao [tex]\left< a,a \right] \times \left< a,a \right][/tex] za bilo koji [tex]a \in \mathbb{R}[/tex]. Tako smo na vježbama spominjali kada smo obrađivali prvu točku primjera [tex]2.9[/tex], a poklapa se i s definicijom [tex]d[/tex]-intervala u primjeru [tex]2.2[/tex] [tex](b)[/tex].
Uglavnom, da, takav dogovor narušava bitno svojstvo da prazan skup ide u nulu (dapače, slika funkcije postaje pravi nadskup od [tex]\left[ 0, +\infty \right][/tex]); no, mislim da se ipak referencira na ovo što navodim pošto je taj dogovor ipak uveden kasnije i uz nešto drugačije područje ovog kolegija.
(A ako misliš da definicija koju ti zadaš nije dovoljno jasna ili precizna, uvijek je dobro napomenuti kako se definicija točno ponaša za prazan skup ili pak njega posebno preslikati u nulu.)
|
|
| [Vrh] |
|
|









