| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
sunny
Forumaš(ica)

Pridružen/a: 21. 01. 2007. (01:06:34)
Postovi: (153)16
|
|
| [Vrh] |
|
sunny
Forumaš(ica)

Pridružen/a: 21. 01. 2007. (01:06:34)
Postovi: (153)16
|
|
| [Vrh] |
|
kkarlo
Forumaš(ica)

Pridružen/a: 19. 05. 2010. (08:43:59)
Postovi: (1B2)16
Spol: 
|
|
| [Vrh] |
|
sunny
Forumaš(ica)

Pridružen/a: 21. 01. 2007. (01:06:34)
Postovi: (153)16
|
|
| [Vrh] |
|
kkarlo
Forumaš(ica)

Pridružen/a: 19. 05. 2010. (08:43:59)
Postovi: (1B2)16
Spol: 
|
 Postano: 23:53 sri, 3. 4. 2013 Naslov: Postano: 23:53 sri, 3. 4. 2013 Naslov: |
    |
|
|
[quote="sunny"]po proslogodisnjim kolokvijima je gradivo za drugi kolokvij, a i po onim pitanjima za kolokvij... takoder, koliko sam skuzila, u prvim kolokvijima nema zadataka sa kodiranjem RAM stroja nego samo teorija, a posto nisam bila na zadnjem predavanju/vjezbama ne znam da li smo te zadatke uopce radili :?[/quote]
Bio sam na zadnjem satu, i nismo radili neke zadatke sa kodiranjem, ali se koristilo neko svojstvo od tamo pri dokazivanju primitivno rekurzivne funkcije...
No evo sto sam si napravio za teoriju za prvi kolokvij, a dokaze sam odlucio preskocit...
Ubacio sam i ove stvari koje mozda i ne treba ucit, al bolje te dvije, tri definicije vise, nego da na kraju ispadne da bas ta dodje u kolokviju...
| sunny (napisa): | po proslogodisnjim kolokvijima je gradivo za drugi kolokvij, a i po onim pitanjima za kolokvij... takoder, koliko sam skuzila, u prvim kolokvijima nema zadataka sa kodiranjem RAM stroja nego samo teorija, a posto nisam bila na zadnjem predavanju/vjezbama ne znam da li smo te zadatke uopce radili  |
Bio sam na zadnjem satu, i nismo radili neke zadatke sa kodiranjem, ali se koristilo neko svojstvo od tamo pri dokazivanju primitivno rekurzivne funkcije...
No evo sto sam si napravio za teoriju za prvi kolokvij, a dokaze sam odlucio preskocit...
Ubacio sam i ove stvari koje mozda i ne treba ucit, al bolje te dvije, tri definicije vise, nego da na kraju ispadne da bas ta dodje u kolokviju...
| Description: |
|

Download |
| Filename: |
Izračunljivost.pdf |
| Filesize: |
259.9 KB |
| Downloaded: |
489 Time(s) |
|
|
| [Vrh] |
|
Cobs
Forumaš(ica)


Pridružen/a: 21. 01. 2008. (13:32:15)
Postovi: (206)16
Spol: 
Lokacija: Geto
|
|
| [Vrh] |
|
Cobs
Forumaš(ica)


Pridružen/a: 21. 01. 2008. (13:32:15)
Postovi: (206)16
Spol: 
Lokacija: Geto
|
 Postano: 3:05 pet, 5. 4. 2013 Naslov: Postano: 3:05 pet, 5. 4. 2013 Naslov: |
    |
|
|
[quote="sunny"]Kako se dokaze da su faktorijeli primitivno rekurzivni?[/quote]
Ja bi to ovak rješio:
(1) prvo bi napisao dokaz da je zbrajanje primitivno rekurzivna funkcija (dokaz ima dva reda i imaš ga u skripti na strani 31)
(2) onda bi dokazao da je množenje prim. rek. Tog dokaza u skripti nema pa
bi napisao da je:
[latex]mult(0,x) = 0\cdot x = 0 = Z(x)[/latex]
znamo da je [latex]Z[/latex] inicijalna funkcija, a klasa prim. rek. funkcija sadrži inicijalne f-je
zatim:
[latex]mult(y+1,x) = (y+1)\cdot x = y\cdot x + x = H(mult(y,x),y,x)[/latex]
sad treba "namjestiti" funkciju [latex]H[/latex]
znamo da je zbrajanje prim. rek. pa ako stavimo da je
[latex]H(y\cdot x,y,x) = add(I^3_1(y\cdot x,y,x),I^3_3(y\cdot x,y,x)) = y\cdot x + x = mult(y+1,x)[/latex]
Sad možemo zaključiti da je funkcija [latex]H[/latex] primitivno rekurzivna zbog jer je kompozicija zbrajanja i projekcija (koje su prim. rek.), pa je i množenje prim. rek. (jer su prim. rek. f-je zatvorene na kompoziciju)
Još treba dokazati ono traženo, a to je dijea je faktorijel prim. rek. pa pogledat samo def. 1.22 u skripti za slučaj kada je k=0
[latex]fact(0) = 1[/latex]
1 je konstanta te samim time prim. rek. (također postoji kratak dokaz u skripti, jedinica je kompozicija funkcija [latex]S_c[/latex] i [latex]Z[/latex])
[latex]fact(y+1) = (y+1)*fact(y) = H(fact(y),y)[/latex]
[latex]H(fact(y),y) = mult(fact(y),y+1) = mult(I^2_1(fact(y),y),S_c(I^2_2(fact(y),y)))[/latex]
Opet je funkcija H kompozicija prim. rek. funkcija pa je samim time i ona prim. rek. tj. faktorijel je primitivno rekurzivna funkcija
| sunny (napisa): | | Kako se dokaze da su faktorijeli primitivno rekurzivni? |
Ja bi to ovak rješio:
(1) prvo bi napisao dokaz da je zbrajanje primitivno rekurzivna funkcija (dokaz ima dva reda i imaš ga u skripti na strani 31)
(2) onda bi dokazao da je množenje prim. rek. Tog dokaza u skripti nema pa
bi napisao da je:
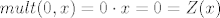
znamo da je 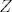 inicijalna funkcija, a klasa prim. rek. funkcija sadrži inicijalne f-je inicijalna funkcija, a klasa prim. rek. funkcija sadrži inicijalne f-je
zatim:
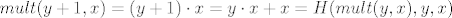
sad treba "namjestiti" funkciju 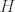
znamo da je zbrajanje prim. rek. pa ako stavimo da je

Sad možemo zaključiti da je funkcija 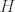 primitivno rekurzivna zbog jer je kompozicija zbrajanja i projekcija (koje su prim. rek.), pa je i množenje prim. rek. (jer su prim. rek. f-je zatvorene na kompoziciju) primitivno rekurzivna zbog jer je kompozicija zbrajanja i projekcija (koje su prim. rek.), pa je i množenje prim. rek. (jer su prim. rek. f-je zatvorene na kompoziciju)
Još treba dokazati ono traženo, a to je dijea je faktorijel prim. rek. pa pogledat samo def. 1.22 u skripti za slučaj kada je k=0
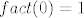
1 je konstanta te samim time prim. rek. (također postoji kratak dokaz u skripti, jedinica je kompozicija funkcija 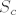 i i 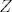 ) )
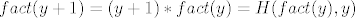
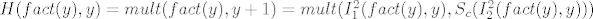
Opet je funkcija H kompozicija prim. rek. funkcija pa je samim time i ona prim. rek. tj. faktorijel je primitivno rekurzivna funkcija
|
|
| [Vrh] |
|
kkarlo
Forumaš(ica)

Pridružen/a: 19. 05. 2010. (08:43:59)
Postovi: (1B2)16
Spol: 
|
 Postano: 7:22 pet, 5. 4. 2013 Naslov: Postano: 7:22 pet, 5. 4. 2013 Naslov: |
    |
|
|
Znam da smo to radili tek kasnije ali da li bi moglo i ovako:
f(x,y)=xy,
napisat kao
f(x,y)={x+x+x+....+x} ukupno y puta.
f(x,y)=[suma(ide od 0 do y-1)](x).
Sada x zapisemo kao projekciju koja je primitivno rekurzivna, pa imamo konacnu sumu primitivno rekurzivnih funkcija te je time i f primitivno rekurzivna?
Jer nismo u dokazu da je ta suma primitivno rekurzivna nigdje koristili da je * primitivno rekurzivna...?
A za faktorijelu je lagano kad imas puta...
Čak možda faktorijelu raspisat preko konačnog produkta onda...
Mislim ako za puta može konačna suma, onda i za faktorijelu može konačni produkt?
Znam da smo to radili tek kasnije ali da li bi moglo i ovako:
f(x,y)=xy,
napisat kao
f(x,y)={x+x+x+....+x} ukupno y puta.
f(x,y)=[suma(ide od 0 do y-1)](x).
Sada x zapisemo kao projekciju koja je primitivno rekurzivna, pa imamo konacnu sumu primitivno rekurzivnih funkcija te je time i f primitivno rekurzivna?
Jer nismo u dokazu da je ta suma primitivno rekurzivna nigdje koristili da je * primitivno rekurzivna...?
A za faktorijelu je lagano kad imas puta...
Čak možda faktorijelu raspisat preko konačnog produkta onda...
Mislim ako za puta može konačna suma, onda i za faktorijelu može konačni produkt?
|
|
| [Vrh] |
|
Cobs
Forumaš(ica)


Pridružen/a: 21. 01. 2008. (13:32:15)
Postovi: (206)16
Spol: 
Lokacija: Geto
|
|
| [Vrh] |
|
kkarlo
Forumaš(ica)

Pridružen/a: 19. 05. 2010. (08:43:59)
Postovi: (1B2)16
Spol: 
|
|
| [Vrh] |
|
50kre
Forumaš(ica)
Pridružen/a: 16. 03. 2011. (19:39:38)
Postovi: (6)16
|
 Postano: 15:50 pon, 8. 4. 2013 Naslov: Postano: 15:50 pon, 8. 4. 2013 Naslov: |
    |
|
|
Pitanje vezano za zadatak iz kolokvija:
Imam fju definiranu sa:
f : S -> N , f(x,y) = max(x,y) - min(x,y) gdje je S={(x+y, x-y): x,y € N} ?
Koliko je f(6,2)? Odnosno čini mi se da je funkcija malo nezgodno definirana. Mislim da korektna interpretacija definicije nalaže da je f(6,2)=6-2=4, no izgleda kao da se je htjelo definirati fju za koju vrijedi f(6,2)=4-2 = 2. Kako ste vi rješavali ovaj zadatak?
Pitanje vezano za zadatak iz kolokvija:
Imam fju definiranu sa:
f : S -> N , f(x,y) = max(x,y) - min(x,y) gdje je S={(x+y, x-y): x,y € N} ?
Koliko je f(6,2)? Odnosno čini mi se da je funkcija malo nezgodno definirana. Mislim da korektna interpretacija definicije nalaže da je f(6,2)=6-2=4, no izgleda kao da se je htjelo definirati fju za koju vrijedi f(6,2)=4-2 = 2. Kako ste vi rješavali ovaj zadatak?
|
|
| [Vrh] |
|
kkarlo
Forumaš(ica)

Pridružen/a: 19. 05. 2010. (08:43:59)
Postovi: (1B2)16
Spol: 
|
 Postano: 16:11 pon, 8. 4. 2013 Naslov: Postano: 16:11 pon, 8. 4. 2013 Naslov: |
    |
|
|
[quote="50kre"]Pitanje vezano za zadatak iz kolokvija:
Imam fju definiranu sa:
f : S -> N , f(x,y) = max(x,y) - min(x,y) gdje je S={(x+y, x-y): x,y € N} ?
Koliko je f(6,2)? Odnosno čini mi se da je funkcija malo nezgodno definirana. Mislim da korektna interpretacija definicije nalaže da je f(6,2)=6-2=4, no izgleda kao da se je htjelo definirati fju za koju vrijedi f(6,2)=4-2 = 2. Kako ste vi rješavali ovaj zadatak?[/quote]
Evo kako:
prvo oduzimam od x-a i y-a dok jedan ne postane nula. Ako je x- postao nula, idem u besk. petlju, ako je y postao nula onda provjeravam koliki je x.
dva put smanjujem x i dvaput povecavam r0. Ako je x paran, tj. na prvom smanjivanju izleti van onda je sve ok, i zaustavljam program, a ako je x neparan onda idem u beskonacnu petlju.
Trebalo je samo skuziti slijedece:
x-y mora biti paran broj, da bi postojali a i b takvi da x=a+b i y=a-b.
Nakon sto se to otkrije je jednostavan postupak, oduzmi od x-a y i provjeri parnost, te ili spremi rez u r0 ili odi u beskon. petlju.
| 50kre (napisa): | Pitanje vezano za zadatak iz kolokvija:
Imam fju definiranu sa:
f : S → N , f(x,y) = max(x,y) - min(x,y) gdje je S={(x+y, x-y): x,y € N} ?
Koliko je f(6,2)? Odnosno čini mi se da je funkcija malo nezgodno definirana. Mislim da korektna interpretacija definicije nalaže da je f(6,2)=6-2=4, no izgleda kao da se je htjelo definirati fju za koju vrijedi f(6,2)=4-2 = 2. Kako ste vi rješavali ovaj zadatak? |
Evo kako:
prvo oduzimam od x-a i y-a dok jedan ne postane nula. Ako je x- postao nula, idem u besk. petlju, ako je y postao nula onda provjeravam koliki je x.
dva put smanjujem x i dvaput povecavam r0. Ako je x paran, tj. na prvom smanjivanju izleti van onda je sve ok, i zaustavljam program, a ako je x neparan onda idem u beskonacnu petlju.
Trebalo je samo skuziti slijedece:
x-y mora biti paran broj, da bi postojali a i b takvi da x=a+b i y=a-b.
Nakon sto se to otkrije je jednostavan postupak, oduzmi od x-a y i provjeri parnost, te ili spremi rez u r0 ili odi u beskon. petlju.
|
|
| [Vrh] |
|
50kre
Forumaš(ica)
Pridružen/a: 16. 03. 2011. (19:39:38)
Postovi: (6)16
|
 Postano: 16:33 pon, 8. 4. 2013 Naslov: Postano: 16:33 pon, 8. 4. 2013 Naslov: |
    |
|
|
[quote="kkarlo"]
Evo kako:
prvo oduzimam od x-a i y-a dok jedan ne postane nula. Ako je x- postao nula, idem u besk. petlju, ako je y postao nula onda provjeravam koliki je x.
dva put smanjujem x i dvaput povecavam r0. Ako je x paran, tj. na prvom smanjivanju izleti van onda je sve ok, i zaustavljam program, a ako je x neparan onda idem u beskonacnu petlju.
Trebalo je samo skuziti slijedece:
x-y mora biti paran broj, da bi postojali a i b takvi da x=a+b i y=a-b.
Nakon sto se to otkrije je jednostavan postupak, oduzmi od x-a y i provjeri parnost, te ili spremi rez u r0 ili odi u beskon. petlju.[/quote]
Dobro ok tako sam i ja rijesio zadatak, odnosno rjesavao sam kao da je f(6,2)=6-2.
Kazem fja je malo nezgodno definirana, zapravo uvijek vrijedi da je f(x,y) = x-y... negdje sam izgubio dosta bodova i mislio sam da je na tom zadatku, odnosno da sam krivo shvatio definiciju te fje ali izgleda da sam negdje drugdje napravio gresku/e. A nista moram cekati srijedu i uvid u kolokvije. Hvala na odgovoru!
| kkarlo (napisa): |
Evo kako:
prvo oduzimam od x-a i y-a dok jedan ne postane nula. Ako je x- postao nula, idem u besk. petlju, ako je y postao nula onda provjeravam koliki je x.
dva put smanjujem x i dvaput povecavam r0. Ako je x paran, tj. na prvom smanjivanju izleti van onda je sve ok, i zaustavljam program, a ako je x neparan onda idem u beskonacnu petlju.
Trebalo je samo skuziti slijedece:
x-y mora biti paran broj, da bi postojali a i b takvi da x=a+b i y=a-b.
Nakon sto se to otkrije je jednostavan postupak, oduzmi od x-a y i provjeri parnost, te ili spremi rez u r0 ili odi u beskon. petlju. |
Dobro ok tako sam i ja rijesio zadatak, odnosno rjesavao sam kao da je f(6,2)=6-2.
Kazem fja je malo nezgodno definirana, zapravo uvijek vrijedi da je f(x,y) = x-y... negdje sam izgubio dosta bodova i mislio sam da je na tom zadatku, odnosno da sam krivo shvatio definiciju te fje ali izgleda da sam negdje drugdje napravio gresku/e. A nista moram cekati srijedu i uvid u kolokvije. Hvala na odgovoru!
|
|
| [Vrh] |
|
kkarlo
Forumaš(ica)

Pridružen/a: 19. 05. 2010. (08:43:59)
Postovi: (1B2)16
Spol: 
|
 Postano: 17:15 pon, 8. 4. 2013 Naslov: Postano: 17:15 pon, 8. 4. 2013 Naslov: |
    |
|
|
[quote="50kre"][quote="kkarlo"]
Evo kako:
prvo oduzimam od x-a i y-a dok jedan ne postane nula. Ako je x- postao nula, idem u besk. petlju, ako je y postao nula onda provjeravam koliki je x.
dva put smanjujem x i dvaput povecavam r0. Ako je x paran, tj. na prvom smanjivanju izleti van onda je sve ok, i zaustavljam program, a ako je x neparan onda idem u beskonacnu petlju.
Trebalo je samo skuziti slijedece:
x-y mora biti paran broj, da bi postojali a i b takvi da x=a+b i y=a-b.
Nakon sto se to otkrije je jednostavan postupak, oduzmi od x-a y i provjeri parnost, te ili spremi rez u r0 ili odi u beskon. petlju.[/quote]
Dobro ok tako sam i ja rijesio zadatak, odnosno rjesavao sam kao da je f(6,2)=6-2.
Kazem fja je malo nezgodno definirana, zapravo uvijek vrijedi da je f(x,y) = x-y... negdje sam izgubio dosta bodova i mislio sam da je na tom zadatku, odnosno da sam krivo shvatio definiciju te fje ali izgleda da sam negdje drugdje napravio gresku/e. A nista moram cekati srijedu i uvid u kolokvije. Hvala na odgovoru![/quote]
Da vrlo vjerojatno. Jer s obzirom na moje bodove, ovaj zadatak mi je morao biti skroz tocan...
I nema na cemu.
:)
| 50kre (napisa): | | kkarlo (napisa): |
Evo kako:
prvo oduzimam od x-a i y-a dok jedan ne postane nula. Ako je x- postao nula, idem u besk. petlju, ako je y postao nula onda provjeravam koliki je x.
dva put smanjujem x i dvaput povecavam r0. Ako je x paran, tj. na prvom smanjivanju izleti van onda je sve ok, i zaustavljam program, a ako je x neparan onda idem u beskonacnu petlju.
Trebalo je samo skuziti slijedece:
x-y mora biti paran broj, da bi postojali a i b takvi da x=a+b i y=a-b.
Nakon sto se to otkrije je jednostavan postupak, oduzmi od x-a y i provjeri parnost, te ili spremi rez u r0 ili odi u beskon. petlju. |
Dobro ok tako sam i ja rijesio zadatak, odnosno rjesavao sam kao da je f(6,2)=6-2.
Kazem fja je malo nezgodno definirana, zapravo uvijek vrijedi da je f(x,y) = x-y... negdje sam izgubio dosta bodova i mislio sam da je na tom zadatku, odnosno da sam krivo shvatio definiciju te fje ali izgleda da sam negdje drugdje napravio gresku/e. A nista moram cekati srijedu i uvid u kolokvije. Hvala na odgovoru! |
Da vrlo vjerojatno. Jer s obzirom na moje bodove, ovaj zadatak mi je morao biti skroz tocan...
I nema na cemu.

|
|
| [Vrh] |
|
Cobs
Forumaš(ica)


Pridružen/a: 21. 01. 2008. (13:32:15)
Postovi: (206)16
Spol: 
Lokacija: Geto
|
|
| [Vrh] |
|
Cobs
Forumaš(ica)


Pridružen/a: 21. 01. 2008. (13:32:15)
Postovi: (206)16
Spol: 
Lokacija: Geto
|
|
| [Vrh] |
|
sunny
Forumaš(ica)

Pridružen/a: 21. 01. 2007. (01:06:34)
Postovi: (153)16
|
|
| [Vrh] |
|
Cobs
Forumaš(ica)


Pridružen/a: 21. 01. 2008. (13:32:15)
Postovi: (206)16
Spol: 
Lokacija: Geto
|
 Postano: 12:17 sri, 29. 5. 2013 Naslov: Postano: 12:17 sri, 29. 5. 2013 Naslov: |
    |
|
|
Definicije i iskazi na jednom papiru, s tim da ne dam ruku u vatru za par definicija, a ni zadnjih par iskaza, s obzirom da istih nema u skripti pa sam ih tražio na par izvora i kombinirao kak mislim da je najlakše shvatljivo o čemu se stvarno radi. Ak ima kakva greška, slobodno me pm-ajte da promijenim.
Definicije i iskazi na jednom papiru, s tim da ne dam ruku u vatru za par definicija, a ni zadnjih par iskaza, s obzirom da istih nema u skripti pa sam ih tražio na par izvora i kombinirao kak mislim da je najlakše shvatljivo o čemu se stvarno radi. Ak ima kakva greška, slobodno me pm-ajte da promijenim.
| Description: |
|

Download |
| Filename: |
teorija2.pdf |
| Filesize: |
126.58 KB |
| Downloaded: |
457 Time(s) |
|
|
| [Vrh] |
|
sunny
Forumaš(ica)

Pridružen/a: 21. 01. 2007. (01:06:34)
Postovi: (153)16
|
|
| [Vrh] |
|
Cobs
Forumaš(ica)


Pridružen/a: 21. 01. 2008. (13:32:15)
Postovi: (206)16
Spol: 
Lokacija: Geto
|
|
| [Vrh] |
|
|
















