Search
 
 
  Engleski
 
 
 
Open in this window (click to change)
Forum@DeGiorgi: Početna
Forum za podršku nastavi na PMF-MO
Login Registracija FAQ Smajlići Članstvo Pretražnik Forum@DeGiorgi: Početna

provjera rijesenja
WWW:

Moja sarma
 
Započnite novu temu   Odgovorite na temu   printer-friendly view    Forum@DeGiorgi: Početna -> Kolegiji 1. godine, preddiplomski studij Matematika -> Matematička analiza 1 i 2
Prethodna tema :: Sljedeća tema  
Autor/ica Poruka
filipnet
Forumaš(ica)
Forumaš(ica)


Pridružen/a: 02. 11. 2003. (01:17:46)
Postovi: (399)16
Spol: muško
Sarma = la pohva - posuda
24 = 29 - 5
Lokacija: cvrsto na stolici
PostPostano: 17:35 pon, 30. 8. 2004    Naslov: provjera rijesenja Citirajte i odgovorite
Razvijte u red potencija oko tocke c=-2 funkciju
[code:1]
ln=(4-2x)/(x+6)[/code:1]
Ja sam dobio -1/2*suma(x+2)^2n/16^n
Da li mozda neko rijesio ovaj zadatak od FMB iz 2. mjeseca?
Razvijte u red potencija oko tocke c=-2 funkciju
Kod:

ln=(4-2x)/(x+6)

Ja sam dobio -1/2*suma(x+2)^2n/16^n
Da li mozda neko rijesio ovaj zadatak od FMB iz 2. mjeseca?



_________________
Dwarf Everything happens with a reason! Vidi me kako skaaaaaceeeem!
[Vrh]
Korisnički profil Pošaljite privatnu poruku
veky
Forumaš(ica)
Forumaš(ica)


Pridružen/a: 09. 12. 2002. (19:59:43)
Postovi: (5B0)16
Sarma = la pohva - posuda
22 = 24 - 2
Lokacija: negdje daleko...
PostPostano: 16:31 uto, 31. 8. 2004    Naslov: Re: provjera rijesenja Citirajte i odgovorite
[quote="filipnet"]Razvijte u red potencija oko tocke c=-2 funkciju
[code:1]
ln=(4-2x)/(x+6)[/code:1]
Ja sam dobio -1/2*suma(x+2)^2n/16^n
Da li mozda neko rijesio ovaj zadatak od FMB iz 2. mjeseca?[/quote]

Još ti fali ln2 ispred, jedan faktor x+2 , i linearno u nazivniku...
ln((4-2x)/(x+6))=ln2-sum{n:0~}((x+2)^(2n+1)/(2^(4n+1)*(2n+1))) .
Kako si rješavao?
filipnet (napisa):
Razvijte u red potencija oko tocke c=-2 funkciju
Kod:

ln=(4-2x)/(x+6)

Ja sam dobio -1/2*suma(x+2)^2n/16^n
Da li mozda neko rijesio ovaj zadatak od FMB iz 2. mjeseca?


Još ti fali ln2 ispred, jedan faktor x+2 , i linearno u nazivniku...
ln((4-2x)/(x+6))=ln2-sum{n:0~}((x+2)^(2n+1)/(2^(4n+1)*(2n+1))) .
Kako si rješavao?


[Vrh]
Korisnički profil Pošaljite privatnu poruku Pošaljite e-mail Posjetite Web stranice
filipnet
Forumaš(ica)
Forumaš(ica)


Pridružen/a: 02. 11. 2003. (01:17:46)
Postovi: (399)16
Spol: muško
Sarma = la pohva - posuda
24 = 29 - 5
Lokacija: cvrsto na stolici
PostPostano: 19:22 uto, 31. 8. 2004    Naslov: Citirajte i odgovorite
Pa prvo sam derivirao ovaj ln i onda dalje razvijao!
Pa prvo sam derivirao ovaj ln i onda dalje razvijao!



_________________
Dwarf Everything happens with a reason! Vidi me kako skaaaaaceeeem!
[Vrh]
Korisnički profil Pošaljite privatnu poruku
veky
Forumaš(ica)
Forumaš(ica)


Pridružen/a: 09. 12. 2002. (19:59:43)
Postovi: (5B0)16
Sarma = la pohva - posuda
22 = 24 - 2
Lokacija: negdje daleko...
PostPostano: 21:02 uto, 31. 8. 2004    Naslov: Citirajte i odgovorite
[quote="filipnet"]Pa prvo sam derivirao ovaj ln i onda dalje razvijao![/quote]

Onda ga nisi dobro derivirao, zaboravio si nultu derivaciju (vrijednost funkcije u -2) ispred, i još ponešto...
filipnet (napisa):
Pa prvo sam derivirao ovaj ln i onda dalje razvijao!


Onda ga nisi dobro derivirao, zaboravio si nultu derivaciju (vrijednost funkcije u -2) ispred, i još ponešto...


[Vrh]
Korisnički profil Pošaljite privatnu poruku Pošaljite e-mail Posjetite Web stranice
filipnet
Forumaš(ica)
Forumaš(ica)


Pridružen/a: 02. 11. 2003. (01:17:46)
Postovi: (399)16
Spol: muško
Sarma = la pohva - posuda
24 = 29 - 5
Lokacija: cvrsto na stolici
PostPostano: 22:28 uto, 31. 8. 2004    Naslov: Citirajte i odgovorite
mislim da sam negdje zeznuo, ajde mala pomoc, hvala!
Doso sam do:
-1/2*(1+(x+2)^2/16 -((x+2)^2/16)^2 + ((x+2)^2/16)^3......
Je dobro tako? :?:
mislim da sam negdje zeznuo, ajde mala pomoc, hvala!
Doso sam do:
-1/2*(1+(x+2)^2/16 -((x+2)^2/16)^2 + ((x+2)^2/16)^3......
Je dobro tako? Question



_________________
Dwarf Everything happens with a reason! Vidi me kako skaaaaaceeeem!
[Vrh]
Korisnički profil Pošaljite privatnu poruku
veky
Forumaš(ica)
Forumaš(ica)


Pridružen/a: 09. 12. 2002. (19:59:43)
Postovi: (5B0)16
Sarma = la pohva - posuda
22 = 24 - 2
Lokacija: negdje daleko...
PostPostano: 9:11 sri, 1. 9. 2004    Naslov: Citirajte i odgovorite
[quote="filipnet"]mislim da sam negdje zeznuo, ajde mala pomoc, hvala!
Doso sam do:
-1/2*(1+(x+2)^2/16 -((x+2)^2/16)^2 + ((x+2)^2/16)^3......
Je dobro tako? :?:[/quote]

Koliko ja vidim, nije... :-/
Mah. Pa znaš razvit ln(1+ž) u red oko ž=0 , zar ne?
(Imaš u svakoj pristojnijoj zbirci formulâ).

Dakle, svedi ga na taj oblik (znaš kako mathematičari kuhaju čaj?; ).
Prvo svedeš ovu -2jku u nulu, jednostavnom transformacijom y=x+2 (odnosno x=y-2 ). Dobiješ ln((4-2y+4)/(y-2+6))=ln(2(4-y)/(y+4)) .

Cilj nam je dobiti ln(1+nešto) , gdje nešto ovisi o y što je moguće jednostavnije - tako da kad to razvijemo u red (ona formula koju ćeš pogledati: ), to također bude jednostavno prepoznati kao red po y , odnosno x+2 , što nam treba. To ćemo ovdje postići rastavljanjem ln-a:

ln2+ln(4-y)-ln(4+y) .
Ove ln(4{+/-}y) napišemo kao ln(4(1+-y/4))=2ln2+ln(1+-(y/4)) ,
i oduzmemo prvi od drugoga. Svaki drugi član u razvoju se dakle poništi, ostali se poduplaju, na početku dobiješ ln2 , i to je to.

Treba još detaljnije?
filipnet (napisa):
mislim da sam negdje zeznuo, ajde mala pomoc, hvala!
Doso sam do:
-1/2*(1+(x+2)^2/16 -((x+2)^2/16)^2 + ((x+2)^2/16)^3......
Je dobro tako? Question


Koliko ja vidim, nije... :-/
Mah. Pa znaš razvit ln(1+ž) u red oko ž=0 , zar ne?
(Imaš u svakoj pristojnijoj zbirci formulâ).

Dakle, svedi ga na taj oblik (znaš kako mathematičari kuhaju čaj?; ).
Prvo svedeš ovu -2jku u nulu, jednostavnom transformacijom y=x+2 (odnosno x=y-2 ). Dobiješ ln((4-2y+4)/(y-2+6))=ln(2(4-y)/(y+4)) .

Cilj nam je dobiti ln(1+nešto) , gdje nešto ovisi o y što je moguće jednostavnije - tako da kad to razvijemo u red (ona formula koju ćeš pogledati: ), to također bude jednostavno prepoznati kao red po y , odnosno x+2 , što nam treba. To ćemo ovdje postići rastavljanjem ln-a:

ln2+ln(4-y)-ln(4+y) .
Ove ln(4{+/-}y) napišemo kao ln(4(1+-y/4))=2ln2+ln(1+-(y/4)) ,
i oduzmemo prvi od drugoga. Svaki drugi član u razvoju se dakle poništi, ostali se poduplaju, na početku dobiješ ln2 , i to je to.

Treba još detaljnije?


[Vrh]
Korisnički profil Pošaljite privatnu poruku Pošaljite e-mail Posjetite Web stranice
filipnet
Forumaš(ica)
Forumaš(ica)


Pridružen/a: 02. 11. 2003. (01:17:46)
Postovi: (399)16
Spol: muško
Sarma = la pohva - posuda
24 = 29 - 5
Lokacija: cvrsto na stolici
PostPostano: 15:16 sri, 1. 9. 2004    Naslov: Citirajte i odgovorite
[quote="veky"]
ln2+ln(4-y)-ln(4+y) .
Ove ln(4{+/-}y) napišemo kao ln(4(1+-y/4))=2ln2+ln(1+-(y/4)) ,
i oduzmemo prvi od drugoga. Svaki drugi član u razvoju se dakle poništi, ostali se poduplaju, na početku dobiješ ln2 , i to je to.

Treba još detaljnije?[/quote]


Do tud sam te skuzio, ali ovo sa ln(4{+/-}y) tu si me malo zbunio! daj mi to jos malo objasni!
veky (napisa):

ln2+ln(4-y)-ln(4+y) .
Ove ln(4{+/-}y) napišemo kao ln(4(1+-y/4))=2ln2+ln(1+-(y/4)) ,
i oduzmemo prvi od drugoga. Svaki drugi član u razvoju se dakle poništi, ostali se poduplaju, na početku dobiješ ln2 , i to je to.

Treba još detaljnije?



Do tud sam te skuzio, ali ovo sa ln(4{+/-}y) tu si me malo zbunio! daj mi to jos malo objasni!



_________________
Dwarf Everything happens with a reason! Vidi me kako skaaaaaceeeem!
[Vrh]
Korisnički profil Pošaljite privatnu poruku
veky
Forumaš(ica)
Forumaš(ica)


Pridružen/a: 09. 12. 2002. (19:59:43)
Postovi: (5B0)16
Sarma = la pohva - posuda
22 = 24 - 2
Lokacija: negdje daleko...
PostPostano: 13:40 čet, 2. 9. 2004    Naslov: Citirajte i odgovorite
[quote="filipnet"][quote="veky"]
ln2+ln(4-y)-ln(4+y) .
Ove ln(4{+/-}y) napišemo kao ln(4(1+-y/4))=2ln2+ln(1+-(y/4)) ,
i oduzmemo prvi od drugoga. Svaki drugi član u razvoju se dakle poništi, ostali se poduplaju, na početku dobiješ ln2 , i to je to.

Treba još detaljnije?[/quote]

Do tud sam te skuzio, ali ovo sa ln(4{+/-}y) tu si me malo zbunio! daj mi to jos malo objasni![/quote]

Pa tu počinje fun part. :-D

Ok, vjerovat ću ti na riječ da si prelistao knjigu i našao gore spomenuti razvoj, koji glasi
[latex]\ln(1+\hat{z})=\sum_n^\omega\frac{(-1)^n\hat{z}^{n+1}}{n+1}[/latex].

Sad znaš da je ln(4+y)=ln(4(1+y/4))=ln4+ln(1+y/4) , te drugi sumand raspišeš kako gore piše. Također isto napraviš s
ln(4-y)=ln4+ln(1+(-y/4)) . E sad, gdje god imaš (-y/4)^nešto , to je zapravo (y/4)^nešto , s predznakom koji je isti ili suprotan ovisno o tome je li nešto parno ili neparno. Dakle gornji redovi su ti oblika
ln(1+y/4)=a+b+c+d+e+f+g+h+....
ln(1-y/4)=a-b+c-d+e-f+g-h+.... ,
pa kad ih oduzmeš (ln4 se ionako poništi) dobiješ
ln(4+y)-ln(4-y)=2b+2d+2f+2h+....
(za odgovarajuće vrijednosti b,d,f,h,....: ). To sad još oduzmeš od ln2 , i dobio si svoj rastav.

Sad jasno?
filipnet (napisa):
veky (napisa):

ln2+ln(4-y)-ln(4+y) .
Ove ln(4{+/-}y) napišemo kao ln(4(1+-y/4))=2ln2+ln(1+-(y/4)) ,
i oduzmemo prvi od drugoga. Svaki drugi član u razvoju se dakle poništi, ostali se poduplaju, na početku dobiješ ln2 , i to je to.

Treba još detaljnije?


Do tud sam te skuzio, ali ovo sa ln(4{+/-}y) tu si me malo zbunio! daj mi to jos malo objasni!


Pa tu počinje fun part. Very Happy

Ok, vjerovat ću ti na riječ da si prelistao knjigu i našao gore spomenuti razvoj, koji glasi
.

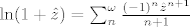Sad znaš da je ln(4+y)=ln(4(1+y/4))=ln4+ln(1+y/4) , te drugi sumand raspišeš kako gore piše. Također isto napraviš s
ln(4-y)=ln4+ln(1+(-y/4)) . E sad, gdje god imaš (-y/4)^nešto , to je zapravo (y/4)^nešto , s predznakom koji je isti ili suprotan ovisno o tome je li nešto parno ili neparno. Dakle gornji redovi su ti oblika
ln(1+y/4)=a+b+c+d+e+f+g+h+....
ln(1-y/4)=a-b+c-d+e-f+g-h+.... ,
pa kad ih oduzmeš (ln4 se ionako poništi) dobiješ
ln(4+y)-ln(4-y)=2b+2d+2f+2h+....
(za odgovarajuće vrijednosti b,d,f,h,....: ). To sad još oduzmeš od ln2 , i dobio si svoj rastav.

Sad jasno?


[Vrh]
Korisnički profil Pošaljite privatnu poruku Pošaljite e-mail Posjetite Web stranice
Prethodni postovi:   
Započnite novu temu   Odgovorite na temu   printer-friendly view    Forum@DeGiorgi: Početna -> Kolegiji 1. godine, preddiplomski studij Matematika -> Matematička analiza 1 i 2 Vremenska zona: GMT + 01:00.
Stranica 1 / 1.

 
Forum(o)Bir:  
Ne možete otvarati nove teme.
Ne možete odgovarati na postove.
Ne možete uređivati Vaše postove.
Ne možete izbrisati Vaše postove.
Ne možete glasovati u anketama.
You can attach files in this forum
You can download files in this forum


Powered by phpBB © 2001, 2002 phpBB Group
Theme created by Vjacheslav Trushkin
HR (Cro) by Ančica Sečan