| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
lucijana
Forumaš(ica)

Pridružen/a: 01. 05. 2008. (01:32:09)
Postovi: (2F)16
Spol: 
|
 Postano: 19:55 pet, 26. 7. 2013 Naslov: Kardinalnosti Postano: 19:55 pet, 26. 7. 2013 Naslov: Kardinalnosti |
    |
|
|
1) Treba izračunati kardinalnosti skupa svih nizova u skupu {1,2,3,4,5}
2) Izračunajte kardinalnosti skupa svih riječi (smislenih i nesmislenih) koji se mogu napraviti od 30 slova hrvatske abecede
3)Izračunajte kardinalnost skupa svih riječi koje se sastoje od 10
samoglasnika
4)Izračunajte kardinalnost skupa X={-1,-3,-5,...} [latex]\subseteq[/latex]Z
Ako može netko pomoći riješiti bila bih mu zahvalna
1) Treba izračunati kardinalnosti skupa svih nizova u skupu {1,2,3,4,5}
2) Izračunajte kardinalnosti skupa svih riječi (smislenih i nesmislenih) koji se mogu napraviti od 30 slova hrvatske abecede
3)Izračunajte kardinalnost skupa svih riječi koje se sastoje od 10
samoglasnika
4)Izračunajte kardinalnost skupa X={-1,-3,-5,...}  Z Z
Ako može netko pomoći riješiti bila bih mu zahvalna
|
|
| [Vrh] |
|
vsego
Site Admin


Pridružen/a: 06. 10. 2002. (22:07:09)
Postovi: (3562)16
Spol: 
Lokacija: /sbin/init
|
 Postano: 21:00 pet, 26. 7. 2013 Naslov: Postano: 21:00 pet, 26. 7. 2013 Naslov: |
    |
|
|
Hintovi:
1. Isto kao i nizovi na skupu [tex]\{0,1,2,3,4\}[/tex], a to je bijektivno sa zapisom relanih brojeva iz skupa [tex][0,1][/tex] u bazi 5.
2. Slicno, ako zamijenis [tex]\text{a} \mapsto 1,\ \text{b} \mapsto 2,\dots[/tex]. Primijeti da su rijeci konacne, sto znaci da vuces bijekciju s brojevima koji imaju konacni decimalni zapis i nemaju nule prije "kraja" decimalnog zapisa, dakle [tex][0,1] \cap \mathbb{Q}[/tex] bez ponesto brojeva.
3. Precizirati: slova koliko god, od cega 10 samoglasnika (malo igranja, no zapravo isto kao prethodno); ili ukupno 10 slova koja su sva samoglasnici (konacno, pa lako izracunas)?
4. [tex]f(x) = (1-x) / 2[/tex] je bijekcija s tvog skupa na [tex]\mathbb{N}[/tex].
Hintovi:
1. Isto kao i nizovi na skupu [tex]\{0,1,2,3,4\}[/tex], a to je bijektivno sa zapisom relanih brojeva iz skupa [tex][0,1][/tex] u bazi 5.
2. Slicno, ako zamijenis [tex]\text{a} \mapsto 1,\ \text{b} \mapsto 2,\dots[/tex]. Primijeti da su rijeci konacne, sto znaci da vuces bijekciju s brojevima koji imaju konacni decimalni zapis i nemaju nule prije "kraja" decimalnog zapisa, dakle [tex][0,1] \cap \mathbb{Q}[/tex] bez ponesto brojeva.
3. Precizirati: slova koliko god, od cega 10 samoglasnika (malo igranja, no zapravo isto kao prethodno); ili ukupno 10 slova koja su sva samoglasnici (konacno, pa lako izracunas)?
4. [tex]f(x) = (1-x) / 2[/tex] je bijekcija s tvog skupa na [tex]\mathbb{N}[/tex].
_________________ U pravilu ignoriram pitanja u krivim topicima i kodove koji nisu u [code]...[/code] blokovima.
Takodjer, OBJASNITE sto vas muci! "Sto mi je krivo?", bez opisa u cemu je problem, rijetko ce zadobiti moju paznju.  |
|
| [Vrh] |
|
lucijana
Forumaš(ica)

Pridružen/a: 01. 05. 2008. (01:32:09)
Postovi: (2F)16
Spol: 
|
|
| [Vrh] |
|
goranm
Forumaš(ica)


Pridružen/a: 12. 11. 2002. (20:09:12)
Postovi: (906)16
Spol: 
|
|
| [Vrh] |
|
inga
Forumaš(ica)

Pridružen/a: 12. 06. 2008. (12:53:49)
Postovi: (27)16
|
|
| [Vrh] |
|
goranm
Forumaš(ica)


Pridružen/a: 12. 11. 2002. (20:09:12)
Postovi: (906)16
Spol: 
|
 Postano: 18:14 sub, 27. 7. 2013 Naslov: Postano: 18:14 sub, 27. 7. 2013 Naslov: |
    |
|
|
[quote="inga"]Izgleda li rješenje ovako:
[latex] f: \mathbb{N} \rightarrow \{1,2,3,4,5\}=5^\aleph= c
[/latex][/quote]
Notacija [tex] \{1,2,3,4,5\}=5^\aleph[/tex] nema smisla.
| inga (napisa): | Izgleda li rješenje ovako:
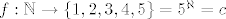 |
Notacija [tex] \{1,2,3,4,5\}=5^\aleph[/tex] nema smisla.
_________________
The Dude Abides
|
|
| [Vrh] |
|
mdoko
Forumaš(ica)


Pridružen/a: 30. 11. 2002. (22:17:12)
Postovi: (71A)16
Spol: 
Lokacija: Heriot-Watt University, Edinburgh
|
 Postano: 18:23 sub, 27. 7. 2013 Naslov: Postano: 18:23 sub, 27. 7. 2013 Naslov: |
    |
|
|
[quote="goranm"][quote="inga"]Izgleda li rješenje ovako:
[latex] f: \mathbb{N} \rightarrow \{1,2,3,4,5\}=5^\aleph= c
[/latex][/quote]
Notacija [tex] \{1,2,3,4,5\}=5^\aleph[/tex] nema smisla.[/quote]
Korektna notacija:
[latex]{\rm{card}}\left(\{f\mid f\colon \mathbb{N} \rightarrow \{1,2,3,4,5\}\}\right) = {\rm{card}}(\{1,2,3,4,5\})^{{\rm{card}}(\mathbb{N})} = 5^{\aleph_0} = c[/latex]
| goranm (napisa): | | inga (napisa): | Izgleda li rješenje ovako:
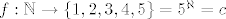 |
Notacija [tex] \{1,2,3,4,5\}=5^\aleph[/tex] nema smisla. |
Korektna notacija:
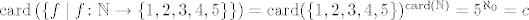
_________________
Extraordinary claims require extraordinary evidence. – Carl Sagan
|
|
| [Vrh] |
|
matematika88888
Forumaš(ica)
Pridružen/a: 18. 09. 2012. (13:45:03)
Postovi: (10)16
|
 Postano: 12:11 pon, 20. 1. 2014 Naslov: Postano: 12:11 pon, 20. 1. 2014 Naslov: |
    |
|
|
Može mi netko pomoći s ovim zadatkom:
a) Izračunati kardinalnost skupa svih nizova točaka u ravnini.
b)Odredite kardinalni broj skupa [latex] {(a_0,a_1,...a_i,...)|a_i \in {1,2,3, i \in N_0}. [/latex]
c) Ispitati kardinalnost skupa [latex] \underline{\prod(X_i)}[/latex] gdje je [latex]X_i[/latex] ekvipotentan sa R , za svaki [latex]i \in Q[/latex].
d) Izračunajte kardinalnost skupa X={-1, -3, -5,...} [latex] \subseteq [/latex] Z.
Može mi netko pomoći s ovim zadatkom:
a) Izračunati kardinalnost skupa svih nizova točaka u ravnini.
b)Odredite kardinalni broj skupa 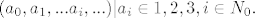
c) Ispitati kardinalnost skupa 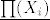 gdje je gdje je 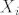 ekvipotentan sa R , za svaki ekvipotentan sa R , za svaki 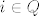 . .
d) Izračunajte kardinalnost skupa X={-1, -3, -5,...}  Z. Z.
|
|
| [Vrh] |
|
mdoko
Forumaš(ica)


Pridružen/a: 30. 11. 2002. (22:17:12)
Postovi: (71A)16
Spol: 
Lokacija: Heriot-Watt University, Edinburgh
|
 Postano: 15:48 pon, 20. 1. 2014 Naslov: Postano: 15:48 pon, 20. 1. 2014 Naslov: |
    |
|
|
[quote="matematika88888"]Može mi netko pomoći s ovim zadatkom:[/quote]
Može, ali u formi kratkih uputa. Nemam baš volje za raspisivanje detalja.
[quote]
a) Izračunati kardinalnost skupa svih nizova točaka u ravnini.
[/quote]
Traži se kardinalnost skupa svih funkcija [tex]f\colon\mathbb{N}\to\mathbb{R}^2[/tex]. To ne bi trebalo biti problem izračunati.
[quote]
b)Odredite kardinalni broj skupa [tex] \{(a_0,a_1,\ldots,a_i,\ldots)\mid a_i \in \{1,2,3\}, i \in N_0\}\}. [/tex]
[/quote]
Traži se kardinalnost skupa svih funkcija [tex]f\colon\mathbb{N}\to\{1,2,3\}[/tex].
[quote]
c) Ispitati kardinalnost skupa [latex] \underline{\prod(X_i)}[/latex] gdje je [latex]X_i[/latex] ekvipotentan sa R , za svaki [latex]i \in Q[/latex].
[/quote]
Nije mi baš jasno što bi ovo potcrtavanje trebalo značiti, ali ignorirajući to, možemo napraviti sljedeće. Uzmimo proizvoljnu bijekciju [tex]\varphi\colon\mathbb{Q}\to\mathbb{N}[/tex]. Očito je da za svaki [tex]i\in\mathbb{Q}[/tex] postoji bijekcija između [tex]X_i[/tex] i intervala [tex]\langle\varphi(i),\varphi(i)+1\rangle[/tex]. Koristeći ovu činjenicu lako je odrediti kardinalnost promatranog skupa.
[quote]
d) Izračunajte kardinalnost skupa [tex]X=\{-1, -3, -5,\ldots\} \subseteq \mathbb{Z}[/tex].[/quote]
Radi se o beskonačnom podskupu prebrojivog skupa. Need I say more?
| matematika88888 (napisa): | | Može mi netko pomoći s ovim zadatkom: |
Može, ali u formi kratkih uputa. Nemam baš volje za raspisivanje detalja.
| Citat: |
a) Izračunati kardinalnost skupa svih nizova točaka u ravnini.
|
Traži se kardinalnost skupa svih funkcija [tex]f\colon\mathbb{N}\to\mathbb{R}^2[/tex]. To ne bi trebalo biti problem izračunati.
| Citat: |
b)Odredite kardinalni broj skupa [tex] \{(a_0,a_1,\ldots,a_i,\ldots)\mid a_i \in \{1,2,3\}, i \in N_0\}\}. [/tex]
|
Traži se kardinalnost skupa svih funkcija [tex]f\colon\mathbb{N}\to\{1,2,3\}[/tex].
| Citat: |
c) Ispitati kardinalnost skupa 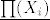 gdje je gdje je 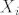 ekvipotentan sa R , za svaki ekvipotentan sa R , za svaki 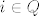 . .
|
Nije mi baš jasno što bi ovo potcrtavanje trebalo značiti, ali ignorirajući to, možemo napraviti sljedeće. Uzmimo proizvoljnu bijekciju [tex]\varphi\colon\mathbb{Q}\to\mathbb{N}[/tex]. Očito je da za svaki [tex]i\in\mathbb{Q}[/tex] postoji bijekcija između [tex]X_i[/tex] i intervala [tex]\langle\varphi(i),\varphi(i)+1\rangle[/tex]. Koristeći ovu činjenicu lako je odrediti kardinalnost promatranog skupa.
| Citat: |
d) Izračunajte kardinalnost skupa [tex]X=\{-1, -3, -5,\ldots\} \subseteq \mathbb{Z}[/tex]. |
Radi se o beskonačnom podskupu prebrojivog skupa. Need I say more?
_________________
Extraordinary claims require extraordinary evidence. – Carl Sagan
|
|
| [Vrh] |
|
matematika88888
Forumaš(ica)
Pridružen/a: 18. 09. 2012. (13:45:03)
Postovi: (10)16
|
 Postano: 13:29 sri, 22. 1. 2014 Naslov: Postano: 13:29 sri, 22. 1. 2014 Naslov: |
    |
|
|
[quote="mdoko"][quote="matematika88888"]Može mi netko pomoći s ovim zadatkom:[/quote]
Može, ali u formi kratkih uputa. Nemam baš volje za raspisivanje detalja.
[quote]
a) Izračunati kardinalnost skupa svih nizova točaka u ravnini.
[/quote]
Traži se kardinalnost skupa svih funkcija [tex]f\colon\mathbb{N}\to\mathbb{R}^2[/tex]. To ne bi trebalo biti problem izračunati.
[quote]
b)Odredite kardinalni broj skupa [tex] \{(a_0,a_1,\ldots,a_i,\ldots)\mid a_i \in \{1,2,3\}, i \in N_0\}\}. [/tex]
[/quote]
Traži se kardinalnost skupa svih funkcija [tex]f\colon\mathbb{N}\to\{1,2,3\}[/tex].
[quote]
c) Ispitati kardinalnost skupa [latex] \underline{\prod(X_i)}[/latex] gdje je [latex]X_i[/latex] ekvipotentan sa R , za svaki [latex]i \in Q[/latex].
[/quote]
Nije mi baš jasno što bi ovo potcrtavanje trebalo značiti, ali ignorirajući to, možemo napraviti sljedeće. Uzmimo proizvoljnu bijekciju [tex]\varphi\colon\mathbb{Q}\to\mathbb{N}[/tex]. Očito je da za svaki [tex]i\in\mathbb{Q}[/tex] postoji bijekcija između [tex]X_i[/tex] i intervala [tex]\langle\varphi(i),\varphi(i)+1\rangle[/tex]. Koristeći ovu činjenicu lako je odrediti kardinalnost promatranog skupa.
[quote]
d) Izračunajte kardinalnost skupa [tex]X=\{-1, -3, -5,\ldots\} \subseteq \mathbb{Z}[/tex].[/quote]
Radi se o beskonačnom podskupu prebrojivog skupa. Need I say more?[/quote]
Znači rješenja su:
a) kard [latex](R^{2 N})=c^{2{\aleph_0}}=c^{\aleph_0}=c[/latex]
b)[latex]3^{\aleph_0}={\aleph_0}^{\aleph_0}=c^{\aleph_0}=c[/latex]
c) [latex]{\aleph_0}^{\aleph_0}=c^{\aleph_0}=c[/latex]
d)[latex]{\aleph_0}[/latex]
?
Hvala puno :-)
| mdoko (napisa): | | matematika88888 (napisa): | | Može mi netko pomoći s ovim zadatkom: |
Može, ali u formi kratkih uputa. Nemam baš volje za raspisivanje detalja.
| Citat: |
a) Izračunati kardinalnost skupa svih nizova točaka u ravnini.
|
Traži se kardinalnost skupa svih funkcija [tex]f\colon\mathbb{N}\to\mathbb{R}^2[/tex]. To ne bi trebalo biti problem izračunati.
| Citat: |
b)Odredite kardinalni broj skupa [tex] \{(a_0,a_1,\ldots,a_i,\ldots)\mid a_i \in \{1,2,3\}, i \in N_0\}\}. [/tex]
|
Traži se kardinalnost skupa svih funkcija [tex]f\colon\mathbb{N}\to\{1,2,3\}[/tex].
| Citat: |
c) Ispitati kardinalnost skupa 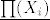 gdje je gdje je 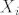 ekvipotentan sa R , za svaki ekvipotentan sa R , za svaki 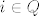 . .
|
Nije mi baš jasno što bi ovo potcrtavanje trebalo značiti, ali ignorirajući to, možemo napraviti sljedeće. Uzmimo proizvoljnu bijekciju [tex]\varphi\colon\mathbb{Q}\to\mathbb{N}[/tex]. Očito je da za svaki [tex]i\in\mathbb{Q}[/tex] postoji bijekcija između [tex]X_i[/tex] i intervala [tex]\langle\varphi(i),\varphi(i)+1\rangle[/tex]. Koristeći ovu činjenicu lako je odrediti kardinalnost promatranog skupa.
| Citat: |
d) Izračunajte kardinalnost skupa [tex]X=\{-1, -3, -5,\ldots\} \subseteq \mathbb{Z}[/tex]. |
Radi se o beskonačnom podskupu prebrojivog skupa. Need I say more? |
Znači rješenja su:
a) kard 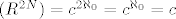
b)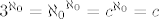
c) 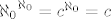
d)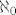
?
Hvala puno 
|
|
| [Vrh] |
|
|











