| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
hendrix
Forumaš(ica)

Pridružen/a: 03. 09. 2012. (15:59:06)
Postovi: (92)16
|
 Postano: 14:24 sub, 3. 11. 2012 Naslov: Postano: 14:24 sub, 3. 11. 2012 Naslov: |
    |
|
|
Greška je ovdje:
[quote="linus"][dtex]l(<-1,\frac{1}{2}>)=arccos(<-1,\frac{1}{2}>)=<0,\frac{\pi}{3}>[/dtex][/quote]
Trebalo bi biti [tex]l\left(\langle-1,\frac{1}{2}\rangle\right)=\arccos \left(\langle-1,\frac{1}{2}\rangle\right)=\langle\frac{\pi}{3},\pi\rangle[/tex]. Primijeti da onda djelovanjem svoje funkcije [tex]h[/tex] dobivaš upravo ono što ovako "nije bilo moguće". :D
btw. za ove oznake, umjesto [tex]<[/tex] i [tex]>[/tex], bolje (i točnije/ljepše :D) funkcionira [code:1]\left \langle \right \rangle[/code:1] :)
Greška je ovdje:
| linus (napisa): | | [dtex]l(←1,\frac{1}{2}>)=arccos(←1,\frac{1}{2}>)=<0,\frac{\pi}{3}>[/dtex] |
Trebalo bi biti [tex]l\left(\langle-1,\frac{1}{2}\rangle\right)=\arccos \left(\langle-1,\frac{1}{2}\rangle\right)=\langle\frac{\pi}{3},\pi\rangle[/tex]. Primijeti da onda djelovanjem svoje funkcije [tex]h[/tex] dobivaš upravo ono što ovako "nije bilo moguće". 
btw. za ove oznake, umjesto [tex]<[/tex] i [tex]>[/tex], bolje (i točnije/ljepše  ) funkcionira ) funkcionira | Kod: | | \left \langle \right \rangle |

|
|
| [Vrh] |
|
Zenon
Forumaš(ica)


Pridružen/a: 09. 09. 2011. (19:14:43)
Postovi: (2B1)16
Sarma: -
Lokacija: [tex]\pm\infty[/tex]
|
 Postano: 15:05 sub, 3. 11. 2012 Naslov: Postano: 15:05 sub, 3. 11. 2012 Naslov: |
    |
|
|
[quote="hendrix"]btw. za ove oznake, umjesto [tex]<[/tex] i [tex]>[/tex], bolje (i točnije/ljepše :D) funkcionira [code:1]\left \langle \right \rangle[/code:1] :)[/quote]
A možeš i [code:1]\left < \right >[/code:1] Razlika je:
Kolega hendrix [tex]\left \langle 1,\frac 32 \right \rangle [/tex].
Kolega ja: [tex]\left < 1,\frac 32\right >[/tex].
U slučaju bez razlomka je:
Kolega hendrix [tex]\left \langle 1,\ 3 \right \rangle [/tex].
Kolega ja: [tex]\left < 1, 3\right >[/tex].
Dakle, potpuno identično, a moje zahtjeva [tex]\leq[/tex] key strikes.
| hendrix (napisa): | btw. za ove oznake, umjesto [tex]<[/tex] i [tex]>[/tex], bolje (i točnije/ljepše  ) funkcionira ) funkcionira | Kod: | | \left \langle \right \rangle |
 |
A možeš i Razlika je:
Kolega hendrix [tex]\left \langle 1,\frac 32 \right \rangle [/tex].
Kolega ja: [tex]\left < 1,\frac 32\right >[/tex].
U slučaju bez razlomka je:
Kolega hendrix [tex]\left \langle 1,\ 3 \right \rangle [/tex].
Kolega ja: [tex]\left < 1, 3\right >[/tex].
Dakle, potpuno identično, a moje zahtjeva [tex]\leq[/tex] key strikes.
|
|
| [Vrh] |
|
linus
Forumaš(ica)


Pridružen/a: 20. 11. 2011. (16:59:13)
Postovi: (46)16
Lokacija: subnet mask
|
 Postano: 17:57 sub, 3. 11. 2012 Naslov: Postano: 17:57 sub, 3. 11. 2012 Naslov: |
    |
|
|
[size=7]Tnx na odgovoru, jos me muci 4. zad gdje treba dokazat monotonost->injektivnost itd. pa je[tex] f(x)=(g o h)(x)[/tex],
[dtex]h(x)=\pi x^2-2\pi x[/dtex]
[dtex]g(x)=cosx[/dtex]
gdje si dobio
[tex]h([0,1])=[0,\pi][/tex]
Taj dio ne shvacam jer je po mom misljenju [tex]h(x)=\pi x^2-2\pi x[/tex] padajuca na [tex][0,1][/tex] (ima pozitivan koef. smjera, pa je tjeme minimum, odnosno [tex]T=(1,-\pi)[/tex], a onda bi bilo [tex]h([0,1])=[-\pi,0][/tex], a tu je onda malo kompliciranije nac inverz jer je [tex]arccosx[/tex] inverz samo za [tex]x\epsilon[0,\pi][/tex][/size]
[color=darkred]Ja sam kriv, updejtao si rjesenja sry[/color]
Tnx na odgovoru, jos me muci 4. zad gdje treba dokazat monotonost→injektivnost itd. pa je[tex] f(x)=(g o h)(x)[/tex],
[dtex]h(x)=\pi x^2-2\pi x[/dtex]
[dtex]g(x)=cosx[/dtex]
gdje si dobio
[tex]h([0,1])=[0,\pi][/tex]
Taj dio ne shvacam jer je po mom misljenju [tex]h(x)=\pi x^2-2\pi x[/tex] padajuca na [tex][0,1][/tex] (ima pozitivan koef. smjera, pa je tjeme minimum, odnosno [tex]T=(1,-\pi)[/tex], a onda bi bilo [tex]h([0,1])=[-\pi,0][/tex], a tu je onda malo kompliciranije nac inverz jer je [tex]arccosx[/tex] inverz samo za [tex]x\epsilon[0,\pi][/tex]
Ja sam kriv, updejtao si rjesenja sry
|
|
| [Vrh] |
|
linus
Forumaš(ica)


Pridružen/a: 20. 11. 2011. (16:59:13)
Postovi: (46)16
Lokacija: subnet mask
|
 Postano: 17:41 ned, 4. 11. 2012 Naslov: Postano: 17:41 ned, 4. 11. 2012 Naslov: |
    |
|
|
nadam se da ima jos nekoga tko jos uvijek uci :lol:
provjera rjesenja, ne kazem da je ovo tocno(dapace lako moguce da nije)
kol. 2011, ona druga grupa (ne pisem sve medukorake) pa evo dakle:
[latex]1. zadatak[/latex],
[latex](a)[/latex]Odredite domenu fje
[latex]f(x)=arccos(x^2-x-1) * 2^{\sqrt{x}}[/latex]
[tex]1^o[/tex]argument za [tex]arccos\ \epsilon\ [-1,1][/tex]
[tex]2^o[/tex] argument za [tex]\sqrt{x}(x\geq0)[/tex]
[tex]x\epsilon[1,2]\cup\{0\}[/tex]
pod (b) nista, 1 bod vise-manje :)
[latex]2. zadatak[/latex]
[latex]f(x)=\frac{\pi}{\pi+2arcsinx}[/latex]
[latex](a)[/latex] Odretite [tex]R_f[/tex]
[tex]f(x)=(k\ o\ g\ o\ h)(x)[/tex]
[tex]h(x)=2arcsinx[/tex]
[tex]g(x)=\pi+x[/tex]
[tex]k(x)=\frac{\pi}{x}[/tex]
[latex]R_f=R_{k\ o\ g\ o\ h}[/latex]
[tex]R_h=[-\pi,\pi][/tex]
[tex]R_g=[0,2\pi][/tex]
[tex]R_k=\left[\frac{1}{2},+\infty\right >[/tex]
[latex](b)[/latex] Odredite skup [tex]S[/tex] t.d. [tex]f:\left <-\frac{1}{2},\frac{1}{2}\right ] ->S[/tex] bude surjekcija, odnosno (po mom misljenju) sliku fje f na [tex]\left <-\frac{1}{2},\frac{1}{2}\right ][/tex] (opet preko kompozicija), ugl dobijem skup [tex]S=\left[\frac{3}{4},\frac{3}{2}\right>[/tex]
[latex]3. zadatak[/latex]
[latex]f(x)=4^{\left\lfloor\frac{2-thx}{1+thx}\right\rfloor-1}[/latex]
Odredite [latex]f^{-1}(\left{4,64\right>)[/latex]
[tex]f(x)=(g_5\ o\ g_4\ o\ g_3\ o\ g_2\ o\ g_1)(x)[/tex]
[tex]g_1(x)=thx[/tex]
[tex]g_2(x)=\frac{2-x}{1+x}[/tex]
[tex]g_3(x)=\left \lfloor x\right\rfloor[/tex]
[tex]g_4(x)=x-1[/tex]
[tex]g_5(x)=4^x[/tex]
Medukorake mogu raspisati ako nekome bas zatreba, ali na kraju sam dobio
[tex]f^{-1}(\left[4,64\right>=\left<arth(-1),arth(0)\right>[/tex]
[latex]4. Zadatak[/latex]
[latex](a) f:\left<-2,-1\right> -> R[/latex]
Dokazite da je f strogo rastuca bijekcija i odredite inverz:
dokaz je analogan onome iz druge grupe(Zenonova rjesenja), a za inverz sam dobio
[latex]f^{-1}(x)=-1-\sqrt{\frac{arcctgx}{\pi}}[/latex]
EDIT: evo, postavih i 3. zad
nadam se da ima jos nekoga tko jos uvijek uci 
provjera rjesenja, ne kazem da je ovo tocno(dapace lako moguce da nije)
kol. 2011, ona druga grupa (ne pisem sve medukorake) pa evo dakle:
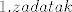 , ,
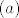 Odredite domenu fje Odredite domenu fje
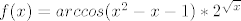
[tex]1^o[/tex]argument za [tex]arccos\ \epsilon\ [-1,1][/tex]
[tex]2^o[/tex] argument za [tex]\sqrt{x}(x\geq0)[/tex]
[tex]x\epsilon[1,2]\cup\{0\}[/tex]
pod (b) nista, 1 bod vise-manje 
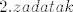
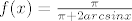
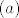 Odretite [tex]R_f[/tex] Odretite [tex]R_f[/tex]
[tex]f(x)=(k\ o\ g\ o\ h)(x)[/tex]
[tex]h(x)=2arcsinx[/tex]
[tex]g(x)=\pi+x[/tex]
[tex]k(x)=\frac{\pi}{x}[/tex]
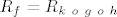
[tex]R_h=[-\pi,\pi][/tex]
[tex]R_g=[0,2\pi][/tex]
[tex]R_k=\left[\frac{1}{2},+\infty\right >[/tex]
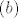 Odredite skup [tex]S[/tex] t.d. [tex]f:\left ←\frac{1}{2},\frac{1}{2}\right ] →S[/tex] bude surjekcija, odnosno (po mom misljenju) sliku fje f na [tex]\left ←\frac{1}{2},\frac{1}{2}\right ][/tex] (opet preko kompozicija), ugl dobijem skup [tex]S=\left[\frac{3}{4},\frac{3}{2}\right>[/tex] Odredite skup [tex]S[/tex] t.d. [tex]f:\left ←\frac{1}{2},\frac{1}{2}\right ] →S[/tex] bude surjekcija, odnosno (po mom misljenju) sliku fje f na [tex]\left ←\frac{1}{2},\frac{1}{2}\right ][/tex] (opet preko kompozicija), ugl dobijem skup [tex]S=\left[\frac{3}{4},\frac{3}{2}\right>[/tex]
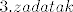
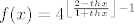
Odredite 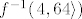
[tex]f(x)=(g_5\ o\ g_4\ o\ g_3\ o\ g_2\ o\ g_1)(x)[/tex]
[tex]g_1(x)=thx[/tex]
[tex]g_2(x)=\frac{2-x}{1+x}[/tex]
[tex]g_3(x)=\left \lfloor x\right\rfloor[/tex]
[tex]g_4(x)=x-1[/tex]
[tex]g_5(x)=4^x[/tex]
Medukorake mogu raspisati ako nekome bas zatreba, ali na kraju sam dobio
[tex]f^{-1}(\left[4,64\right>=\left<arth(-1),arth(0)\right>[/tex]
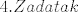
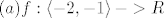
Dokazite da je f strogo rastuca bijekcija i odredite inverz:
dokaz je analogan onome iz druge grupe(Zenonova rjesenja), a za inverz sam dobio
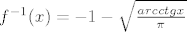
EDIT: evo, postavih i 3. zad
|
|
| [Vrh] |
|
pllook
Forumaš(ica)

Pridružen/a: 08. 11. 2013. (20:56:12)
Postovi: (CD)16
Spol: 
|
 Postano: 14:11 uto, 19. 11. 2013 Naslov: Postano: 14:11 uto, 19. 11. 2013 Naslov: |
    |
|
|
Zadatak glasi: Odredi prirodnu domenu funkcije f(x)=ln(logx(2x^2-5*x+3))
(znači ovaj x je u bazi logaritma)
E sad,ja sam dobila rj <0, 1/2> U <2,+beskonačno>, a rješenje bi trebalo biti <1/2, 1> U <2,+beskonačno>. Pa ako netko vidi grešku bila bih zahvalna.
Zadatak glasi: Odredi prirodnu domenu funkcije f(x)=ln(logx(2x^2-5*x+3))
(znači ovaj x je u bazi logaritma)
E sad,ja sam dobila rj <0, 1/2> U <2,+beskonačno>, a rješenje bi trebalo biti <1/2, 1> U <2,+beskonačno>. Pa ako netko vidi grešku bila bih zahvalna.
|
|
| [Vrh] |
|
kslaven
Forumaš(ica)

Pridružen/a: 17. 10. 2010. (18:07:06)
Postovi: (52)16
Spol: 
|
 Postano: 16:29 uto, 19. 11. 2013 Naslov: Postano: 16:29 uto, 19. 11. 2013 Naslov: |
    |
|
|
[quote="pllook"]Zadatak glasi: Odredi prirodnu domenu funkcije f(x)=ln(logx(2x^2-5*x+3))
(znači ovaj x je u bazi logaritma)
E sad,ja sam dobila rj <0, 1/2> U <2,+beskonačno>, a rješenje bi trebalo biti <1/2, 1> U <2,+beskonačno>. Pa ako netko vidi grešku bila bih zahvalna.[/quote]
Jedan od uvjeta na [tex]x[/tex] je i [dtex]\log_{x}(2x^{2}-5x+3)>0.[/dtex]
Tu nejednadžbu rješavate o ovisnosti o tome je li [tex]0<x<1[/tex] ili [tex]x>1[/tex]. Kada je [tex]0<x<1[/tex] ona prelazi u [dtex]2x^{2}-5x+3<x^{0}=1[/dtex]
jer je [tex]\log_{x}[/tex] strogo padajuća f-ja za [tex]0<x<1[/tex]. Rješavanjem [dtex]2x^{2}-5x+3<1[/dtex] dobit ćete [tex]x\in<1/2,2>\cap<0,1>=<1/2,1>.[/tex] Pretpostavljam da je tu bila greška...
| pllook (napisa): | Zadatak glasi: Odredi prirodnu domenu funkcije f(x)=ln(logx(2x^2-5*x+3))
(znači ovaj x je u bazi logaritma)
E sad,ja sam dobila rj <0, 1/2> U <2,+beskonačno>, a rješenje bi trebalo biti <1/2, 1> U <2,+beskonačno>. Pa ako netko vidi grešku bila bih zahvalna. |
Jedan od uvjeta na [tex]x[/tex] je i [dtex]\log_{x}(2x^{2}-5x+3)>0.[/dtex]
Tu nejednadžbu rješavate o ovisnosti o tome je li [tex]0<x<1[/tex] ili [tex]x>1[/tex]. Kada je [tex]0<x<1[/tex] ona prelazi u [dtex]2x^{2}-5x+3<x^{0}=1[/dtex]
jer je [tex]\log_{x}[/tex] strogo padajuća f-ja za [tex]0<x<1[/tex]. Rješavanjem [dtex]2x^{2}-5x+3<1[/dtex] dobit ćete [tex]x\in<1/2,2>\cap<0,1>=<1/2,1>.[/tex] Pretpostavljam da je tu bila greška...
|
|
| [Vrh] |
|
pllook
Forumaš(ica)

Pridružen/a: 08. 11. 2013. (20:56:12)
Postovi: (CD)16
Spol: 
|
 Postano: 17:01 uto, 19. 11. 2013 Naslov: Postano: 17:01 uto, 19. 11. 2013 Naslov: |
    |
|
|
[quote="kslaven"][quote="pllook"]Zadatak glasi: Odredi prirodnu domenu funkcije f(x)=ln(logx(2x^2-5*x+3))
(znači ovaj x je u bazi logaritma)
E sad,ja sam dobila rj <0, 1/2> U <2,+beskonačno>, a rješenje bi trebalo biti <1/2, 1> U <2,+beskonačno>. Pa ako netko vidi grešku bila bih zahvalna.[/quote]
Jedan od uvjeta na [tex]x[/tex] je i [dtex]\log_{x}(2x^{2}-5x+3)>0.[/dtex]
Tu nejednadžbu rješavate o ovisnosti o tome je li [tex]0<x<1[/tex] ili [tex]x>1[/tex]. Kada je [tex]0<x<1[/tex] ona prelazi u [dtex]2x^{2}-5x+3<x^{0}=1[/dtex]
jer je [tex]\log_{x}[/tex] strogo padajuća f-ja za [tex]0<x<1[/tex]. Rješavanjem [dtex]2x^{2}-5x+3<1[/dtex] dobit ćete [tex]x\in<1/2,2>\cap<0,1>=<1/2,1>.[/tex] Pretpostavljam da je tu bila greška...[/quote]
Hvala!
| kslaven (napisa): | | pllook (napisa): | Zadatak glasi: Odredi prirodnu domenu funkcije f(x)=ln(logx(2x^2-5*x+3))
(znači ovaj x je u bazi logaritma)
E sad,ja sam dobila rj <0, 1/2> U <2,+beskonačno>, a rješenje bi trebalo biti <1/2, 1> U <2,+beskonačno>. Pa ako netko vidi grešku bila bih zahvalna. |
Jedan od uvjeta na [tex]x[/tex] je i [dtex]\log_{x}(2x^{2}-5x+3)>0.[/dtex]
Tu nejednadžbu rješavate o ovisnosti o tome je li [tex]0<x<1[/tex] ili [tex]x>1[/tex]. Kada je [tex]0<x<1[/tex] ona prelazi u [dtex]2x^{2}-5x+3<x^{0}=1[/dtex]
jer je [tex]\log_{x}[/tex] strogo padajuća f-ja za [tex]0<x<1[/tex]. Rješavanjem [dtex]2x^{2}-5x+3<1[/dtex] dobit ćete [tex]x\in<1/2,2>\cap<0,1>=<1/2,1>.[/tex] Pretpostavljam da je tu bila greška... |
Hvala!
|
|
| [Vrh] |
|
četiri
Forumaš(ica)


Pridružen/a: 11. 09. 2012. (20:20:15)
Postovi: (1B)16
Lokacija: Zagreb
|
 Postano: 13:43 ned, 24. 11. 2013 Naslov: Postano: 13:43 ned, 24. 11. 2013 Naslov: |
    |
|
|
[quote="linus"]
[latex]3. zadatak[/latex]
[latex]f(x)=4^{\left\lfloor\frac{2-thx}{1+thx}\right\rfloor-1}[/latex]
Odredite [latex]f^{-1}(\left{4,64\right>)[/latex]
[tex]f(x)=(g_5\ o\ g_4\ o\ g_3\ o\ g_2\ o\ g_1)(x)[/tex]
[tex]g_1(x)=thx[/tex]
[tex]g_2(x)=\frac{2-x}{1+x}[/tex]
[tex]g_3(x)=\left \lfloor x\right\rfloor[/tex]
[tex]g_4(x)=x-1[/tex]
[tex]g_5(x)=4^x[/tex]
Medukorake mogu raspisati ako nekome bas zatreba, ali na kraju sam dobio
[tex]f^{-1}(\left[4,64\right>=\left<arth(-1),arth(0)\right>[/tex]
[/quote]
jel može neko objasnit međukorake ili nešto? zato što meni konačno rješenje ispadne [tex]f^{-1}(\left[4,64\right>)=\left<Arth(-2/5),Arth(0)\right][/tex]
također me zanima zašto su u rješenju oba intervala otvorena? i također me zanima zašto [tex]Arth(0)[/tex] nije zapisano kao [tex]0[/tex].
| linus (napisa): |
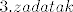
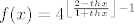
Odredite 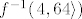
[tex]f(x)=(g_5\ o\ g_4\ o\ g_3\ o\ g_2\ o\ g_1)(x)[/tex]
[tex]g_1(x)=thx[/tex]
[tex]g_2(x)=\frac{2-x}{1+x}[/tex]
[tex]g_3(x)=\left \lfloor x\right\rfloor[/tex]
[tex]g_4(x)=x-1[/tex]
[tex]g_5(x)=4^x[/tex]
Medukorake mogu raspisati ako nekome bas zatreba, ali na kraju sam dobio
[tex]f^{-1}(\left[4,64\right>=\left<arth(-1),arth(0)\right>[/tex]
|
jel može neko objasnit međukorake ili nešto? zato što meni konačno rješenje ispadne [tex]f^{-1}(\left[4,64\right>)=\left<Arth(-2/5),Arth(0)\right][/tex]
također me zanima zašto su u rješenju oba intervala otvorena? i također me zanima zašto [tex]Arth(0)[/tex] nije zapisano kao [tex]0[/tex].
|
|
| [Vrh] |
|
Shirohige
Forumaš(ica)

Pridružen/a: 16. 11. 2012. (20:19:56)
Postovi: (ED)16
Spol: 
|
|
| [Vrh] |
|
zds
Forumaš(ica)
Pridružen/a: 26. 10. 2013. (21:44:04)
Postovi: (D)16
Spol: 
|
|
| [Vrh] |
|
Shirohige
Forumaš(ica)

Pridružen/a: 16. 11. 2012. (20:19:56)
Postovi: (ED)16
Spol: 
|
|
| [Vrh] |
|
pllook
Forumaš(ica)

Pridružen/a: 08. 11. 2013. (20:56:12)
Postovi: (CD)16
Spol: 
|
 Postano: 16:56 ned, 24. 11. 2013 Naslov: Postano: 16:56 ned, 24. 11. 2013 Naslov: |
    |
|
|
[latex]2. zadatak[/latex]
[latex]f(x)=\frac{\pi}{\pi+2arcsinx}[/latex]
[latex](a)[/latex] Odretite [tex]R_f[/tex]
[tex]f(x)=(k\ o\ g\ o\ h)(x)[/tex]
[tex]h(x)=2arcsinx[/tex]
[tex]g(x)=\pi+x[/tex]
[tex]k(x)=\frac{\pi}{x}[/tex]
[latex]R_f=R_{k\ o\ g\ o\ h}[/latex]
[tex]R_h=[-\pi,\pi][/tex]
[tex]R_g=[0,2\pi][/tex]
[tex]R_k=\left[\frac{1}{2},+\infty\right >[/tex]/quote
zašto je Rk=[1/2,+beskonačno>, a ne [0, 1/2] ?
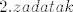
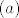 Odretite [tex]R_f[/tex] Odretite [tex]R_f[/tex]
[tex]f(x)=(k\ o\ g\ o\ h)(x)[/tex]
[tex]h(x)=2arcsinx[/tex]
[tex]g(x)=\pi+x[/tex]
[tex]k(x)=\frac{\pi}{x}[/tex]
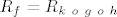
[tex]R_h=[-\pi,\pi][/tex]
[tex]R_g=[0,2\pi][/tex]
[tex]R_k=\left[\frac{1}{2},+\infty\right >[/tex]/quote
zašto je Rk=[1/2,+beskonačno>, a ne [0, 1/2] ?
|
|
| [Vrh] |
|
četiri
Forumaš(ica)


Pridružen/a: 11. 09. 2012. (20:20:15)
Postovi: (1B)16
Lokacija: Zagreb
|
 Postano: 17:06 ned, 24. 11. 2013 Naslov: Postano: 17:06 ned, 24. 11. 2013 Naslov: |
    |
|
|
[quote="pllook"]zašto je Rk=[1/2,+beskonačno>, a ne [0, 1/2] ?[/quote]
nacrtaj graf od pi/x, skica izgleda isto ko i 1/x, i onda lako sa skice grafa pročitaš i dođeš do odgovora....
| pllook (napisa): | | zašto je Rk=[1/2,+beskonačno>, a ne [0, 1/2] ? |
nacrtaj graf od pi/x, skica izgleda isto ko i 1/x, i onda lako sa skice grafa pročitaš i dođeš do odgovora....
|
|
| [Vrh] |
|
zds
Forumaš(ica)
Pridružen/a: 26. 10. 2013. (21:44:04)
Postovi: (D)16
Spol: 
|
|
| [Vrh] |
|
Shirohige
Forumaš(ica)

Pridružen/a: 16. 11. 2012. (20:19:56)
Postovi: (ED)16
Spol: 
|
|
| [Vrh] |
|
ivana_dbk
Forumaš(ica)

Pridružen/a: 27. 10. 2013. (14:24:17)
Postovi: (1D)16
|
|
| [Vrh] |
|
Shirohige
Forumaš(ica)

Pridružen/a: 16. 11. 2012. (20:19:56)
Postovi: (ED)16
Spol: 
|
|
| [Vrh] |
|
ivana_dbk
Forumaš(ica)

Pridružen/a: 27. 10. 2013. (14:24:17)
Postovi: (1D)16
|
|
| [Vrh] |
|
room
Forumaš(ica)

Pridružen/a: 03. 11. 2013. (15:41:40)
Postovi: (78)16
Spol: 
|
 Postano: 21:10 ned, 24. 11. 2013 Naslov: Postano: 21:10 ned, 24. 11. 2013 Naslov: |
    |
|
|
[quote="Shirohige"]Ima netko da je rješavao 2006/2007, zad 5?
1. stranica, Zad 5:
[url]http://web.math.pmf.unizg.hr/nastava/analiza/kol/ma1-0607-kol1.pdf[/url]
Ja sam dobio:
a) Nije surjekcija
b) [tex]-\arcsin(\sqrt{x+3} - 1) - \pi[/tex][/quote]
Zašto je ovaj minus ispred arkusa sinusa? :?
[b]EDIT: [/b]
Taj prvi zadatak iz 2008/2009 je meni ispao kao wolfram alphi, domena su svi x-evi manji od 0.5.
Ovaj dio kod arctg ne trebate ni gledati jer je arctg definiran na cijelom R-u. Gledate ovaj dio sa arcth, on je definiran [tex]\langle -1,1 \rangle[/tex], znači da morate raditi:
[tex]-1 < \frac{1+x}{2-x} < 1[/tex]
Ovo s lijeva će biti za svaki x iz R, a s desna ćete dobiti da su manji od 0.5
Zašto je ovaj minus ispred arkusa sinusa? 
EDIT:
Taj prvi zadatak iz 2008/2009 je meni ispao kao wolfram alphi, domena su svi x-evi manji od 0.5.
Ovaj dio kod arctg ne trebate ni gledati jer je arctg definiran na cijelom R-u. Gledate ovaj dio sa arcth, on je definiran [tex]\langle -1,1 \rangle[/tex], znači da morate raditi:
[tex]-1 < \frac{1+x}{2-x} < 1[/tex]
Ovo s lijeva će biti za svaki x iz R, a s desna ćete dobiti da su manji od 0.5
|
|
| [Vrh] |
|
Shirohige
Forumaš(ica)

Pridružen/a: 16. 11. 2012. (20:19:56)
Postovi: (ED)16
Spol: 
|
 Postano: 21:29 ned, 24. 11. 2013 Naslov: Postano: 21:29 ned, 24. 11. 2013 Naslov: |
    |
|
|
[quote="room"]Zašto je ovaj minus ispred arkusa sinusa? :?[/quote]
Original rješenje je (pa kad se srede pi-evi, dobi se ovo gore):
[tex]\pi-\arcsin(\sqrt{x+3} - 1) - 2\pi[/tex]
[quote]
[b]EDIT: [/b]
Taj prvi zadatak iz 2008/2009 je meni ispao kao wolfram alphi, domena su svi x-evi manji od 0.5.
Ovaj dio kod arctg ne trebate ni gledati jer je arctg definiran na cijelom R-u. Gledate ovaj dio sa arcth, on je definiran [tex]\langle -1,1 \rangle[/tex], znači da morate raditi:
[tex]-1 < \frac{1+x}{2-x} < 1[/tex]
Ovo s lijeva će biti za svaki x iz R, a s desna ćete dobiti da su manji od 0.5[/quote]
Area tangens hiperbolni je definiran za -1 do 1, prema šalabahteru je Arcth = Area kotangens hiperbolni dok je za wolfram alphu to area tangens hiperbolni, znači domena te funkcije je od -beskonačno do -1 i od 1 do +beskonačno (ako se ravnamo prema oznakama sa službenog šalabahtera, a ne prema wolfram alphi).
| room (napisa): | Zašto je ovaj minus ispred arkusa sinusa?  |
Original rješenje je (pa kad se srede pi-evi, dobi se ovo gore):
[tex]\pi-\arcsin(\sqrt{x+3} - 1) - 2\pi[/tex]
| Citat: |
EDIT:
Taj prvi zadatak iz 2008/2009 je meni ispao kao wolfram alphi, domena su svi x-evi manji od 0.5.
Ovaj dio kod arctg ne trebate ni gledati jer je arctg definiran na cijelom R-u. Gledate ovaj dio sa arcth, on je definiran [tex]\langle -1,1 \rangle[/tex], znači da morate raditi:
[tex]-1 < \frac{1+x}{2-x} < 1[/tex]
Ovo s lijeva će biti za svaki x iz R, a s desna ćete dobiti da su manji od 0.5 |
Area tangens hiperbolni je definiran za -1 do 1, prema šalabahteru je Arcth = Area kotangens hiperbolni dok je za wolfram alphu to area tangens hiperbolni, znači domena te funkcije je od -beskonačno do -1 i od 1 do +beskonačno (ako se ravnamo prema oznakama sa službenog šalabahtera, a ne prema wolfram alphi).
Zadnja promjena: Shirohige; 21:35 ned, 24. 11. 2013; ukupno mijenjano 1 put.
|
|
| [Vrh] |
|
|
















