| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
pedro
Forumaš(ica)

Pridružen/a: 21. 10. 2010. (14:08:21)
Postovi: (19B)16
|
|
| [Vrh] |
|
Phoenix
Forumaš(ica)


Pridružen/a: 15. 05. 2010. (18:46:07)
Postovi: (164)16
Sarma: -
|
 Postano: 10:46 čet, 1. 11. 2012 Naslov: Postano: 10:46 čet, 1. 11. 2012 Naslov: |
    |
|
|
Neka je [tex]c \in \mathbb{R}^n[/tex] proizvoljan. Želimo pokazati da je [tex]f[/tex] diferencijabilna u [tex]c[/tex].
Dakle, treba pronaći linearni operator [tex]L : \mathbb{R}^n \rightarrow \mathbb{R}^n[/tex] takav da vrijedi:
[tex]\displaystyle \lim_{x \rightarrow c} \frac{||f(x)-f(c)-L(x-c)||}{||x-c||}=0[/tex].
Tvrdim da je traženi operator zadan s [tex]L(x)=x[/tex]. Provjerimo:
[tex]\displaystyle \lim_{x \rightarrow c} \frac{||f(x)-f(c)-L(x-c)||}{||x-c||} = \lim_{x \rightarrow c} \frac{||x-c-(x-c)||}{||x-c||} = \lim_{x \rightarrow c} \frac{0}{||x-c||} = \lim_{x \rightarrow c} 0 = 0[/tex]
Dakle, zaista postoji takav linearni operator, stoga je [tex]f[/tex] diferencijabilna u [tex]c[/tex].
Jer je [tex]c \in \mathbb{R}^n[/tex] proizvoljan, [tex]f[/tex] je diferencijabilna na cijelom [tex]\mathbb{R}^n[/tex].
P. S. Ako te zanima kako sam se dosjetio ovog operatora, uz samu pretpostavku da je funkcija diferencijabilna (što se nekako i vidi) pogledao sam Jacobijevu matricu i iz nje (kako je ona zapisana u paru kanonskih baza [tex](e,e)[/tex], [tex]e[/tex] je kanonska baza iz [tex]\mathbb{R}^n[/tex]) sam iščitao kako izgleda sam operator.
Neka je [tex]c \in \mathbb{R}^n[/tex] proizvoljan. Želimo pokazati da je [tex]f[/tex] diferencijabilna u [tex]c[/tex].
Dakle, treba pronaći linearni operator [tex]L : \mathbb{R}^n \rightarrow \mathbb{R}^n[/tex] takav da vrijedi:
[tex]\displaystyle \lim_{x \rightarrow c} \frac{||f(x)-f(c)-L(x-c)||}{||x-c||}=0[/tex].
Tvrdim da je traženi operator zadan s [tex]L(x)=x[/tex]. Provjerimo:
[tex]\displaystyle \lim_{x \rightarrow c} \frac{||f(x)-f(c)-L(x-c)||}{||x-c||} = \lim_{x \rightarrow c} \frac{||x-c-(x-c)||}{||x-c||} = \lim_{x \rightarrow c} \frac{0}{||x-c||} = \lim_{x \rightarrow c} 0 = 0[/tex]
Dakle, zaista postoji takav linearni operator, stoga je [tex]f[/tex] diferencijabilna u [tex]c[/tex].
Jer je [tex]c \in \mathbb{R}^n[/tex] proizvoljan, [tex]f[/tex] je diferencijabilna na cijelom [tex]\mathbb{R}^n[/tex].
P. S. Ako te zanima kako sam se dosjetio ovog operatora, uz samu pretpostavku da je funkcija diferencijabilna (što se nekako i vidi) pogledao sam Jacobijevu matricu i iz nje (kako je ona zapisana u paru kanonskih baza [tex](e,e)[/tex], [tex]e[/tex] je kanonska baza iz [tex]\mathbb{R}^n[/tex]) sam iščitao kako izgleda sam operator.
|
|
| [Vrh] |
|
Loo
Forumaš(ica)


Pridružen/a: 11. 06. 2012. (16:02:07)
Postovi: (D0)16
Spol: 
|
 Postano: 18:42 sub, 12. 10. 2013 Naslov: Postano: 18:42 sub, 12. 10. 2013 Naslov: |
    |
|
|
nekolicina kolega me mailom pitala kako riješiti drugi zadatak iz prvog blica s vježbi 2010/2011 pa ću rješenje staviti ovdje u slučaju da još nekome zatreba.
http://web.math.pmf.unizg.hr/nastava/difraf/dif/2010-11/Blic11011.pdf
raspisivanjem uvjeta dobivamo:
[tex]x^2+y^2=\max\{|x|,|y|\}[/tex]
Sada je zgodno primjetiti da uvrštavanjem [tex]-x[/tex] umjesto [tex]x[/tex], odnosno [tex]-y[/tex] umjesto [tex]y[/tex] dobivamo istu jednakost pa je slika simetrična s obzirom na obje koordinatne osi.
Dakle, dovoljno je znati ju nacrtati u prvom kvadrantu! (ovo nam olakšava stvar jer bi inače imali malo više slučajeva)
Znači imamo [tex]x\geq0, y\geq 0 \Rightarrow |x|=x, |y|=y [/tex]
[tex]1°)[/tex] [tex]y\leq x[/tex]
[tex]x^2+y^2=x \\ x^2-x+y^2=0 \\ x^2-x+\frac{1}{4}+y^2=\frac{1}{4} \\ (x-\frac{1}{2})^2+y^2=\frac{1}{4}[/tex]
Znači u prvom kvadrantu ispod pravca [tex]y=x[/tex], radi se o [tex]S((\frac{1}{2}, 0), \frac{1}{2})[/tex] (dio te kružnice u prvom kvadrantu koji je ispod spomenutog pravca).
[tex]2°)[/tex] [tex]y>x[/tex]
Iz [tex]x^2+y^2=y[/tex] na analogan način kao gore dobivamo [tex]x^2+(y-\frac{1}{2})^2=\frac{1}{4}[/tex]
Dakle, u prvom kvadrantu iznad [tex]y=x[/tex] imamo [tex]S((0,\frac{1}{2}), \frac{1}{2})[/tex] (dio u prvom kvadrantu iznad spomenutog pravca).
I sada kad simetrično preslikamo dobivenu sliku preko apcise, a zatim preko ordinate, dobivamo nešto poput djeteline:
[url=http://postimage.org/][img]http://s22.postimg.org/rw4mv6yep/slika.gif[/img][/url]
(na slici se možda baš i ne vidi ali treba naglasiti da je i ishodište u tom skupu)
nekolicina kolega me mailom pitala kako riješiti drugi zadatak iz prvog blica s vježbi 2010/2011 pa ću rješenje staviti ovdje u slučaju da još nekome zatreba.
http://web.math.pmf.unizg.hr/nastava/difraf/dif/2010-11/Blic11011.pdf
raspisivanjem uvjeta dobivamo:
[tex]x^2+y^2=\max\{|x|,|y|\}[/tex]
Sada je zgodno primjetiti da uvrštavanjem [tex]-x[/tex] umjesto [tex]x[/tex], odnosno [tex]-y[/tex] umjesto [tex]y[/tex] dobivamo istu jednakost pa je slika simetrična s obzirom na obje koordinatne osi.
Dakle, dovoljno je znati ju nacrtati u prvom kvadrantu! (ovo nam olakšava stvar jer bi inače imali malo više slučajeva)
Znači imamo [tex]x\geq0, y\geq 0 \Rightarrow |x|=x, |y|=y [/tex]
[tex]1°)[/tex] [tex]y\leq x[/tex]
[tex]x^2+y^2=x \\ x^2-x+y^2=0 \\ x^2-x+\frac{1}{4}+y^2=\frac{1}{4} \\ (x-\frac{1}{2})^2+y^2=\frac{1}{4}[/tex]
Znači u prvom kvadrantu ispod pravca [tex]y=x[/tex], radi se o [tex]S((\frac{1}{2}, 0), \frac{1}{2})[/tex] (dio te kružnice u prvom kvadrantu koji je ispod spomenutog pravca).
[tex]2°)[/tex] [tex]y>x[/tex]
Iz [tex]x^2+y^2=y[/tex] na analogan način kao gore dobivamo [tex]x^2+(y-\frac{1}{2})^2=\frac{1}{4}[/tex]
Dakle, u prvom kvadrantu iznad [tex]y=x[/tex] imamo [tex]S((0,\frac{1}{2}), \frac{1}{2})[/tex] (dio u prvom kvadrantu iznad spomenutog pravca).
I sada kad simetrično preslikamo dobivenu sliku preko apcise, a zatim preko ordinate, dobivamo nešto poput djeteline:

(na slici se možda baš i ne vidi ali treba naglasiti da je i ishodište u tom skupu)
|
|
| [Vrh] |
|
hendrix
Forumaš(ica)

Pridružen/a: 03. 09. 2012. (15:59:06)
Postovi: (92)16
|
|
| [Vrh] |
|
gflegar
Forumaš(ica)


Pridružen/a: 12. 10. 2011. (15:03:41)
Postovi: (10D)16
Spol: 
|
|
| [Vrh] |
|
marsupial
Forumaš(ica)

Pridružen/a: 09. 01. 2012. (22:46:33)
Postovi: (63)16
Spol: 
|
|
| [Vrh] |
|
delilah01.
Forumaš(ica)
Pridružen/a: 10. 11. 2011. (22:50:23)
Postovi: (39)16
|
|
| [Vrh] |
|
marsupial
Forumaš(ica)

Pridružen/a: 09. 01. 2012. (22:46:33)
Postovi: (63)16
Spol: 
|
|
| [Vrh] |
|
4017
Forumaš(ica)

Pridružen/a: 11. 03. 2012. (20:55:09)
Postovi: (17)16
|
|
| [Vrh] |
|
Loo
Forumaš(ica)


Pridružen/a: 11. 06. 2012. (16:02:07)
Postovi: (D0)16
Spol: 
|
 Postano: 20:01 ned, 15. 12. 2013 Naslov: Postano: 20:01 ned, 15. 12. 2013 Naslov: |
    |
|
|
ne određuješ [latex]Df[/latex] u točkama, nego djelovanje diferencijala [latex]Df[/latex] u točki [latex](0,\frac{\pi}{6})[/latex] na vektor [latex](2,-\frac{\pi}{3})[/latex].
to radiš tako da izračunaš [latex]\nabla f(x,y)[/latex] i onda uvrstiš [latex](x,y)=(0,\frac{\pi}{6})[/latex], tj odrediš [latex]\nabla f(0,\frac{\pi}{6})[/latex].
to ti je matrični prikaz u linearnog operatora [latex]Df(0,\frac{\pi}{6})[/latex] u paru kanonskih baza.
i sad djelovanje [latex]Df(0,\frac{\pi}{6})[/latex] na vektor [latex](2,-\frac{\pi}{3})[/latex] određuješ kao na linearnoj - množenjem matričnog prikaza operatora ([latex]\nabla f(0,\frac{\pi}{6})[/latex]) sa zadanim vektorom (rješenje je opet vektor iz [latex]\mathbb{R}^2[/latex]).
ne određuješ 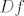 u točkama, nego djelovanje diferencijala u točkama, nego djelovanje diferencijala 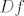 u točki u točki 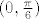 na vektor na vektor 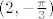 . .
to radiš tako da izračunaš 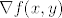 i onda uvrstiš i onda uvrstiš 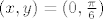 , tj odrediš , tj odrediš 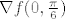 . .
to ti je matrični prikaz u linearnog operatora 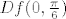 u paru kanonskih baza. u paru kanonskih baza.
i sad djelovanje 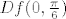 na vektor na vektor 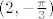 određuješ kao na linearnoj - množenjem matričnog prikaza operatora ( određuješ kao na linearnoj - množenjem matričnog prikaza operatora (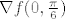 ) sa zadanim vektorom (rješenje je opet vektor iz ) sa zadanim vektorom (rješenje je opet vektor iz 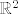 ). ).
|
|
| [Vrh] |
|
4017
Forumaš(ica)

Pridružen/a: 11. 03. 2012. (20:55:09)
Postovi: (17)16
|
|
| [Vrh] |
|
4017
Forumaš(ica)

Pridružen/a: 11. 03. 2012. (20:55:09)
Postovi: (17)16
|
|
| [Vrh] |
|
Loo
Forumaš(ica)


Pridružen/a: 11. 06. 2012. (16:02:07)
Postovi: (D0)16
Spol: 
|
 Postano: 9:12 čet, 2. 1. 2014 Naslov: Postano: 9:12 čet, 2. 1. 2014 Naslov: |
    |
|
|
Označimo [latex]F_1(x,y,z)=x^3+y^3-z, \; F_2(x,y,z)=x^2-2y^2-3z^2-4[/latex].
Sad je tangencijalna ravnina prve plohe u [latex](1,2,9)[/latex] ravnina s vektorom normale [latex]grad F_1(1,2,9)[/latex] koja prolazi točkom [latex](1,2,9)[/latex].
Normala druge plohe je pravac smjera [latex]grad F_2(3,1,-1)[/latex] koji prolazi točkom [latex](3,1,-1)[/latex] (iz ovog lako odrediš kanonski oblik jednadžbe normale)
I sad presjek određuješ kao na elementarnoj 2 - kanonski oblik pravca pretvoriš u parametarski i uvrstiš dobivene koordinate u jednadžbu ravnine, iz čega dobiješ traženi parametar (ako presjek postoji), a time i koordinate točke presjeka.
Označimo 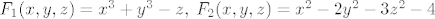 . .
Sad je tangencijalna ravnina prve plohe u 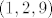 ravnina s vektorom normale ravnina s vektorom normale 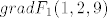 koja prolazi točkom koja prolazi točkom 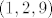 . .
Normala druge plohe je pravac smjera 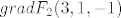 koji prolazi točkom koji prolazi točkom 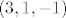 (iz ovog lako odrediš kanonski oblik jednadžbe normale) (iz ovog lako odrediš kanonski oblik jednadžbe normale)
I sad presjek određuješ kao na elementarnoj 2 - kanonski oblik pravca pretvoriš u parametarski i uvrstiš dobivene koordinate u jednadžbu ravnine, iz čega dobiješ traženi parametar (ako presjek postoji), a time i koordinate točke presjeka.
|
|
| [Vrh] |
|
krki
Forumaš(ica)

Pridružen/a: 06. 07. 2011. (20:30:12)
Postovi: (2E)16
|
|
| [Vrh] |
|
Loo
Forumaš(ica)


Pridružen/a: 11. 06. 2012. (16:02:07)
Postovi: (D0)16
Spol: 
|
 Postano: 9:34 sub, 4. 1. 2014 Naslov: Postano: 9:34 sub, 4. 1. 2014 Naslov: |
    |
|
|
2.)
Stavimo [latex]F_1(x,y,z)=x^2+(y-\alpha)^2+z^2-3, \; F_2(x,y,z)=(x-1)^2+y^2+z^2-1[/latex]
Sad tražimo [latex]\alpha[/latex] t.d. [latex]F_1(x_0,y_0,z_0)=0=F_2(x_0, y_0, z_0) \Rightarrow (gradF_1(x_0, y_0, z_0)|grad F_2(x_0, y_0, z_0)=0[/latex]
Jer su ravnine okomite ako su im vektori normala okomiti, a to znači da je skalarni produkt vektora normale nula.
Također, bitno je da presjek postoji, odnosno da postoji točka [latex](x_0, y_0, z_0)[/latex] tako da je premisa u gornjoj implikaciji ispunjena.
[latex]grad F_1(x_0, y_0, z_0)=(2x_0, \; 2(y_0-\alpha), \; 2z_0)[/latex]
[latex]grad F_1(x_0, y_0, z_0)=(2(x_0-1), \; 2y_0, \; 2z_0)[/latex]
Sad uvrstimo izračunato u uvjet [latex](gradF_1(x_0, y_0, z_0)|grad F_2(x_0, y_0, z_0)=0[/latex] i podijelimo izraz s [latex]4[/latex] pa dobijemo:
[latex]x_0(x_0-1)+y_0(y_0-\alpha)+z_0^2=0[/latex]
[latex](x_0-1+1)(x_0-1)+y_0^2+z_0^2-\alpha y_0=0[/latex]
[latex](x_0-1)^2+y_0^2+z_0^2+(x_0-1)-\alpha y_0=0[/latex]
Sad iskoristimo uvjet da je [latex]F_2(x_0, y_0, z_0)=0[/latex], odnosno
[latex](x_0-1)^2+y_0^2+z_0^2=1[/latex].
[latex]1+x_0-1-\alpha y_0=0 \Rightarrow x_0=\alpha y_0[/latex]
Sad oduzmemo jednadžbe [latex]F_1(x_0,y_0,z_0)=0, \; F_2(x_0, y_0, z_0)=0[/latex]
pa imamo:
[latex]2x_0-1-2\alpha y_0 + \alpha ^2 -2=0[/latex]
Uvrstimo [latex]x_0=\alpha y_0[/latex]:
[latex]\alpha ^2=3 \Rightarrow \alpha= \pm \sqrt{3}[/latex]
4.)
Treba samo odrediti formulu za taj volumen u ovisnosti o točki u kojoj je tangencijalna ravnina. (ispast će konstanta)
[latex]F(x,y,z)=xyz-1[/latex]
[latex]grad F(x,y,z)=(yz, \; xz, \; xy)[/latex]
Sad je jednadžba tangencijalne ravnine u [latex](x_0, y_0, z_0)[/latex]:
[latex]y_0z_0(x-x_0)+x_0z_0(y-y_0)+x_0y_0(z-z_0)=0[/latex]
[latex]y_0z_0x+x_0z_0y+x_0y_0z-3x_0y_0z_0=0[/latex]
Vrijedi [latex]x_0y_0z_0=1[/latex], pa je jednadžba:
[latex]y_0z_0x+x_0z_0y+x_0y_0z-3=0[/latex]
Da bi odredili volumen piramide, moramo odrediti sjecišta s koordinatnim osima, odnosno točke [latex](x_1, 0, 0), \; (0, y_1, 0), \; (0, 0, z_1)[/latex] koje leže na ravnini.
Onda je traženi volumen [latex]\frac{1}{6}|x_1 y_1 z_1|[/latex]
Lako dobijemo:
[latex]x_1=\frac{3}{y_0 z_0}, \; y_1=\frac {3}{x_0 z_0}, \; z_1=\frac {3}{x_0 y_0}[/latex]
(uoči da za točke s plohe vrijedi [latex]x_0\neq 0, \; y_0 \neq 0, \; z_0 \neq 0[/latex] pa su gornji nazivnici različiti od nule)
[latex]V(x_0, y_0, z_0)=\frac {27}{6(x_0 y_0 z_0)^2}=\frac{27}{6\cdot 1}=\frac {9}{2}[/latex]
2.)
Stavimo 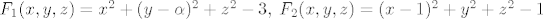
Sad tražimo  t.d. t.d. 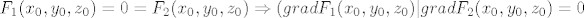
Jer su ravnine okomite ako su im vektori normala okomiti, a to znači da je skalarni produkt vektora normale nula.
Također, bitno je da presjek postoji, odnosno da postoji točka 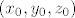 tako da je premisa u gornjoj implikaciji ispunjena. tako da je premisa u gornjoj implikaciji ispunjena.
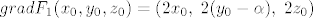
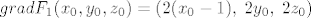
Sad uvrstimo izračunato u uvjet 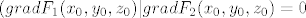 i podijelimo izraz s i podijelimo izraz s  pa dobijemo: pa dobijemo:
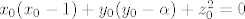
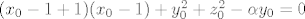

Sad iskoristimo uvjet da je 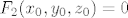 , odnosno , odnosno
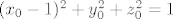 . .
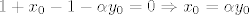
Sad oduzmemo jednadžbe 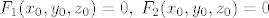
pa imamo:
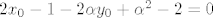
Uvrstimo 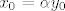 : :
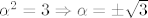
4.)
Treba samo odrediti formulu za taj volumen u ovisnosti o točki u kojoj je tangencijalna ravnina. (ispast će konstanta)
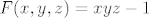
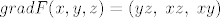
Sad je jednadžba tangencijalne ravnine u 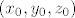 : :

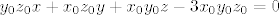
Vrijedi 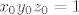 , pa je jednadžba: , pa je jednadžba:
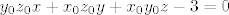
Da bi odredili volumen piramide, moramo odrediti sjecišta s koordinatnim osima, odnosno točke 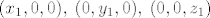 koje leže na ravnini. koje leže na ravnini.
Onda je traženi volumen 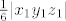
Lako dobijemo:
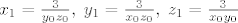
(uoči da za točke s plohe vrijedi 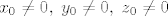 pa su gornji nazivnici različiti od nule) pa su gornji nazivnici različiti od nule)
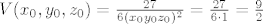
|
|
| [Vrh] |
|
krki
Forumaš(ica)

Pridružen/a: 06. 07. 2011. (20:30:12)
Postovi: (2E)16
|
|
| [Vrh] |
|
marsupial
Forumaš(ica)

Pridružen/a: 09. 01. 2012. (22:46:33)
Postovi: (63)16
Spol: 
|
 Postano: 16:06 pon, 6. 1. 2014 Naslov: Postano: 16:06 pon, 6. 1. 2014 Naslov: |
    |
|
|
[quote="Loo"]Označimo [latex]F_1(x,y,z)=x^3+y^3-z, \; F_2(x,y,z)=x^2-2y^2-3z^2-4[/latex].
Sad je tangencijalna ravnina prve plohe u [latex](1,2,9)[/latex] ravnina s vektorom normale [latex]grad F_1(1,2,9)[/latex] koja prolazi točkom [latex](1,2,9)[/latex].
Normala druge plohe je pravac smjera [latex]grad F_2(3,1,-1)[/latex] koji prolazi točkom [latex](3,1,-1)[/latex] (iz ovog lako odrediš kanonski oblik jednadžbe normale)
I sad presjek određuješ kao na elementarnoj 2 - kanonski oblik pravca pretvoriš u parametarski i uvrstiš dobivene koordinate u jednadžbu ravnine, iz čega dobiješ traženi parametar (ako presjek postoji), a time i koordinate točke presjeka.[/quote]
Da li je rješenje možda (19/8, 31/21, 2/7) ? (ako je netko rješavao)
| Loo (napisa): | Označimo 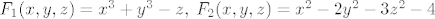 . .
Sad je tangencijalna ravnina prve plohe u 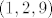 ravnina s vektorom normale ravnina s vektorom normale 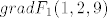 koja prolazi točkom koja prolazi točkom 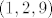 . .
Normala druge plohe je pravac smjera 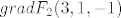 koji prolazi točkom koji prolazi točkom 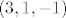 (iz ovog lako odrediš kanonski oblik jednadžbe normale) (iz ovog lako odrediš kanonski oblik jednadžbe normale)
I sad presjek određuješ kao na elementarnoj 2 - kanonski oblik pravca pretvoriš u parametarski i uvrstiš dobivene koordinate u jednadžbu ravnine, iz čega dobiješ traženi parametar (ako presjek postoji), a time i koordinate točke presjeka. |
Da li je rješenje možda (19/8, 31/21, 2/7) ? (ako je netko rješavao)
|
|
| [Vrh] |
|
marsupial
Forumaš(ica)

Pridružen/a: 09. 01. 2012. (22:46:33)
Postovi: (63)16
Spol: 
|
|
| [Vrh] |
|
Loo
Forumaš(ica)


Pridružen/a: 11. 06. 2012. (16:02:07)
Postovi: (D0)16
Spol: 
|
 Postano: 22:35 pon, 6. 1. 2014 Naslov: Postano: 22:35 pon, 6. 1. 2014 Naslov: |
    |
|
|
[quote="marsupial"]
Da li je rješenje možda (19/8, 31/21, 2/7) ? (ako je netko rješavao)[/quote]
Meni je ispalo [latex](\frac{11}{3}, \frac{5}{9}, -\frac{1}{3})[/latex].
A što se ovog prvog iz 09/10 tiče, rješenje bi išlo nekako ovako:
Jednadžba tangencijalne ravnine je [latex]6(x-3)+10(y+5)+8(z-4)=0[/latex], a xz-ravnine [latex]y=0[/latex].
I sad, općenito, presjek dviju ravnina u [latex]\mathbb{R}^3[/latex] je ili prazan (ak su paralelne i nisu iste) ili ravnina (ak su iste) ili pravac.
Očito ove dvije nisu niti paralelne, niti iste, pa će presjek biti pravac.
(ovo pričam jer je zgodno znati kakvo rješenje da očekujemo)
I sad taj pravac određuješ tako da riješiš sustav:
[latex]6(x-3)+10(y+5)+8(z-4)=0[/latex]
[latex]y=0[/latex]
Možeš npr. u gornju jednadžbu uvrstiti [latex]y=0[/latex], pa dobiješ [latex]z=-\frac{3}{4}x[/latex].
I onda staviš [latex]x=t[/latex], pa ti je kanonski oblik pravca:
[latex]\frac{x}{1}=\frac{y}{0}=\frac{z}{-\frac{3}{4}}[/latex]
| marsupial (napisa): |
Da li je rješenje možda (19/8, 31/21, 2/7) ? (ako je netko rješavao) |
Meni je ispalo 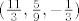 . .
A što se ovog prvog iz 09/10 tiče, rješenje bi išlo nekako ovako:
Jednadžba tangencijalne ravnine je 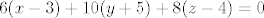 , a xz-ravnine , a xz-ravnine 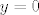 . .
I sad, općenito, presjek dviju ravnina u 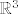 je ili prazan (ak su paralelne i nisu iste) ili ravnina (ak su iste) ili pravac. je ili prazan (ak su paralelne i nisu iste) ili ravnina (ak su iste) ili pravac.
Očito ove dvije nisu niti paralelne, niti iste, pa će presjek biti pravac.
(ovo pričam jer je zgodno znati kakvo rješenje da očekujemo)
I sad taj pravac određuješ tako da riješiš sustav:
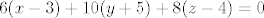
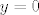
Možeš npr. u gornju jednadžbu uvrstiti 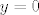 , pa dobiješ , pa dobiješ 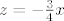 . .
I onda staviš 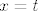 , pa ti je kanonski oblik pravca: , pa ti je kanonski oblik pravca:
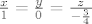
|
|
| [Vrh] |
|
marsupial
Forumaš(ica)

Pridružen/a: 09. 01. 2012. (22:46:33)
Postovi: (63)16
Spol: 
|
 Postano: 23:01 pon, 6. 1. 2014 Naslov: Postano: 23:01 pon, 6. 1. 2014 Naslov: |
    |
|
|
zlato si! fala ti :)
hm.. ovak, ja sam za ovaj 2008/2009 za drugu plohu dobila tangencijalnu ravninu 6(x-3)-4(y-1)+6(z+1)=0
kanonski sam ju zapisala (x-3)/6 = (y-1)/(-4) = (z+1)/6
dobila x=3+6L, y=1-4L, z=1+6L
uvrstila u tangencijalnu ravninu prve i dobila da mi je L= -5/42
i kada sam nazad uvrstila u x, y i z dobila sam ona rješenja
jesam x, y i z u krivu jednadžbu uvrstila?
zlato si! fala ti 
hm.. ovak, ja sam za ovaj 2008/2009 za drugu plohu dobila tangencijalnu ravninu 6(x-3)-4(y-1)+6(z+1)=0
kanonski sam ju zapisala (x-3)/6 = (y-1)/(-4) = (z+1)/6
dobila x=3+6L, y=1-4L, z=1+6L
uvrstila u tangencijalnu ravninu prve i dobila da mi je L= -5/42
i kada sam nazad uvrstila u x, y i z dobila sam ona rješenja
jesam x, y i z u krivu jednadžbu uvrstila?
|
|
| [Vrh] |
|
|















