Vjerojatnost da ćeš dobiti pismo u jednom bacanju je 1/2, pa je vjerojatnost da ćeš dobiti n pisama u n bacanja (1/2)^n. Daklem odabereš minimalni n takav da je šansa da su sve pisma a to je (1/2)^n < 5%, što je n = 5 jer je tad (1/2)^n = 0,03125 što je po prvi put < 5%.
Morat ćeš još koji put pomnožit s 1/2 da dobiješ < 1%.
Ovo drugo ista stvar, samo umjesto 1/2 potenciraš 99/100 jer je šansa da ne dobiješ stotku u jednom bacanju 99/100, pa je u n bacanja šansa da nijedno nije stotka (99/100)^n.
dakle broj potrebnih bacanja je cca [latex]\log_{1-\frac{1}{N}} 0.05[/latex], što se, ako je vjerovati [url=http://www.wolframalpha.com/input/?i=log+base+%281-1%2Fx%29+of+0.05+from+0+to+10]alphi[/url], ponaša više-manje linearno
Ovo cca je najveće ili najmanje cijelo ne znam sad :D
Vjerojatnost da ćeš dobiti pismo u jednom bacanju je 1/2, pa je vjerojatnost da ćeš dobiti n pisama u n bacanja (1/2)^n. Daklem odabereš minimalni n takav da je šansa da su sve pisma a to je (1/2)^n < 5%, što je n = 5 jer je tad (1/2)^n = 0,03125 što je po prvi put < 5%.
Morat ćeš još koji put pomnožit s 1/2 da dobiješ < 1%.
Ovo drugo ista stvar, samo umjesto 1/2 potenciraš 99/100 jer je šansa da ne dobiješ stotku u jednom bacanju 99/100, pa je u n bacanja šansa da nijedno nije stotka (99/100)^n.
dakle broj potrebnih bacanja je cca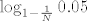 
, što se, ako je vjerovati alphi, ponaša više-manje linearno
Ovo cca je najveće ili najmanje cijelo ne znam sad 
_________________
Nikola Adžaga
Građevinski fakultet, Sveučilište u Zagrebu
