| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
Loo
Forumaš(ica)


Pridružen/a: 11. 06. 2012. (16:02:07)
Postovi: (D0)16
Spol: 
|
 Postano: 7:35 sri, 11. 12. 2013 Naslov: Postano: 7:35 sri, 11. 12. 2013 Naslov: |
    |
|
|
U biti ti je najbolje ovu funkciju gledati kao [latex]f:\mathbb{R}^{2n} \to \mathbb{R}^n[/latex].
Jer svaki uređen par vektora iz [latex]\mathbb{R}^n \times \mathbb{R}^n[/latex] možemo shvatiti kao [latex]2n[/latex]-torku iz [latex]\mathbb{R}^{2n}[/latex] i obrnuto, svaki vektor iz [latex]\mathbb{R}^{2n}[/latex] možemo shvatiti kao uređen par vektora iz [latex]\mathbb{R}^n \times \mathbb{R}^n[/latex].
Onda imaš:
[latex]
f(x_1,...,x_n,y_1,...,y_n)=e^{y_1a_1+...+y_na_n}(x_1,...,x_n)=(x_1e^{y_1a_1+...+y_na_n},...,x_ne^{y_1a_1+...+y_na_n})[/latex]
Parcijalne derivacije su:
[latex]\begin{displaymath} \frac{\partial f_i}{\partial x_j}(x,y)=\left\{
\begin{array}{lr}
0 , & i\neq j\\
e^{y_1a_1+...+y_na_n}, & i=j
\end{array}
\right.
\end{displaymath} [/latex]
[latex]\frac{\partial f_i}{\partial y_j}(x,y)=a_jx_ie^{y_1a_1+...+y_na_n}[/latex]
Zanima nas diferencijal u točki [latex](0,a)[/latex], odnosno [latex](0,...,0,a_1,...,a_n)[/latex] pa možemo odmah uvrstiti te točke u dobivene parcijalne derivacije. Imamo:
[latex]\frac{\partial f_i}{\partial x_i}(0,a)=e^{a_1^2+...+a_n^2}=e^{\|a\|^2}[/latex]
[latex]\frac{\partial f_i}{\partial y_j}(0,a)=0[/latex]
Znači da je zapravo matrica od [latex]Df(0,a) \; n\times 2n[/latex] matrica, pri čemu je prvi [latex]n\times n[/latex] dio dijagonalna marica s [latex]e^{\|a\|^2}[/latex] na dijagonali, a ostalo su nule. Tj. zadnjih [latex]n[/latex] stupaca su nul stupci:
[latex]Df(0,a)= \begin{pmatrix}
e^{\|a\|^2} & 0 & \cdots & 0 & \cdots & 0 \\
0 & e^{\|a\|^2} & \cdots & 0 & \cdots & 0\\
\vdots & \vdots & \ddots & \vdots \\
0 & 0 & \cdots & e^{\|a\|^2 & \cdots & 0}
\end{pmatrix}[/latex]
I sad lako dobiješ [latex]Df(0,a)(1,...,1)[/latex]
Uoči, mogli smo umjesto [latex](x_1,...,x_n,y_1,...,y_n)[/latex] varijable zvati [latex](x_1,...,x_{2n})[/latex] kao što smo i navikli u [latex]\mathbb{R}^{2n}[/latex], ali nekako nam je čitav zadatak zadan na način da posebno gledamo prvih [latex]n[/latex] i posebno drugih [latex]n[/latex] varijabli pa je ovako malo ljepše.
U biti ti je najbolje ovu funkciju gledati kao 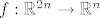 . .
Jer svaki uređen par vektora iz 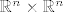 možemo shvatiti kao možemo shvatiti kao 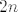 -torku iz -torku iz 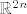 i obrnuto, svaki vektor iz i obrnuto, svaki vektor iz 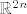 možemo shvatiti kao uređen par vektora iz možemo shvatiti kao uređen par vektora iz 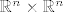 . .
Onda imaš:
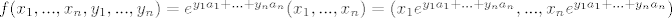
Parcijalne derivacije su:
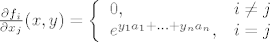
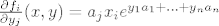
Zanima nas diferencijal u točki 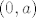 , odnosno , odnosno 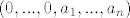 pa možemo odmah uvrstiti te točke u dobivene parcijalne derivacije. Imamo: pa možemo odmah uvrstiti te točke u dobivene parcijalne derivacije. Imamo:
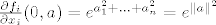
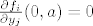
Znači da je zapravo matrica od 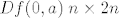 matrica, pri čemu je prvi matrica, pri čemu je prvi 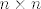 dio dijagonalna marica s dio dijagonalna marica s 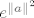 na dijagonali, a ostalo su nule. Tj. zadnjih na dijagonali, a ostalo su nule. Tj. zadnjih  stupaca su nul stupci: stupaca su nul stupci:
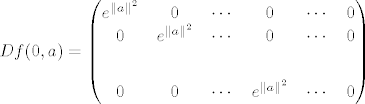
I sad lako dobiješ 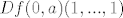
Uoči, mogli smo umjesto 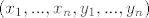 varijable zvati varijable zvati 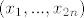 kao što smo i navikli u kao što smo i navikli u 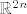 , ali nekako nam je čitav zadatak zadan na način da posebno gledamo prvih , ali nekako nam je čitav zadatak zadan na način da posebno gledamo prvih  i posebno drugih i posebno drugih  varijabli pa je ovako malo ljepše. varijabli pa je ovako malo ljepše.
|
|
| [Vrh] |
|
marsupial
Forumaš(ica)

Pridružen/a: 09. 01. 2012. (22:46:33)
Postovi: (63)16
Spol: 
|
|
| [Vrh] |
|
matkec
Forumaš(ica)


Pridružen/a: 14. 05. 2010. (16:21:29)
Postovi: (8C)16
|
|
| [Vrh] |
|
marsupial
Forumaš(ica)

Pridružen/a: 09. 01. 2012. (22:46:33)
Postovi: (63)16
Spol: 
|
|
| [Vrh] |
|
marička
Forumaš(ica)

Pridružen/a: 27. 05. 2011. (14:57:58)
Postovi: (31)16
Spol: 
|
|
| [Vrh] |
|
krki
Forumaš(ica)

Pridružen/a: 06. 07. 2011. (20:30:12)
Postovi: (2E)16
|
|
| [Vrh] |
|
acuksi
Forumaš(ica)
Pridružen/a: 23. 09. 2012. (21:23:13)
Postovi: (F)16
|
|
| [Vrh] |
|
krki
Forumaš(ica)

Pridružen/a: 06. 07. 2011. (20:30:12)
Postovi: (2E)16
|
|
| [Vrh] |
|
acuksi
Forumaš(ica)
Pridružen/a: 23. 09. 2012. (21:23:13)
Postovi: (F)16
|
|
| [Vrh] |
|
marsupial
Forumaš(ica)

Pridružen/a: 09. 01. 2012. (22:46:33)
Postovi: (63)16
Spol: 
|
|
| [Vrh] |
|
thepineapple
Forumaš(ica)

Pridružen/a: 03. 11. 2011. (18:58:15)
Postovi: (12)16
|
|
| [Vrh] |
|
Loo
Forumaš(ica)


Pridružen/a: 11. 06. 2012. (16:02:07)
Postovi: (D0)16
Spol: 
|
 Postano: 21:03 sub, 15. 2. 2014 Naslov: Postano: 21:03 sub, 15. 2. 2014 Naslov: |
    |
|
|
Skup [tex]K[/tex] je zapravo jednak [tex][-2,2]\times [-2,2][/tex] jer je [tex]\max \{|x|, |y| \} \leq 2[/tex] akko [tex]|x|\leq 2, \; |y|\leq 2[/tex].
Radi se o kompaktnom skupu, a funkcija je neprekidna, pa maksimum i minimum sigurno postoje. Ako se te vrijednosti postižu unutar kocke (na interioru), onda su to i lokalni ekstremi funkcije, pa su nužno stacionarne točke. Ako nisu unutra, onda moraju biti na rubu kocke.
Znači nađeš stacionarne točke na [tex]Int K=\langle -2, 2 \rangle \times \langle -2, 2 \rangle [/tex] i najveću i najmanju vrijednost na rubovima, tj. za [tex]|x|=2[/tex], [tex]|y|=2[/tex] i onda pogledaš u kojima od tih stacionarnih točaka i ovih točaka s rubova je vrijednost najveća/najmanja.
Skup [tex]K[/tex] je zapravo jednak [tex][-2,2]\times [-2,2][/tex] jer je [tex]\max \{|x|, |y| \} \leq 2[/tex] akko [tex]|x|\leq 2, \; |y|\leq 2[/tex].
Radi se o kompaktnom skupu, a funkcija je neprekidna, pa maksimum i minimum sigurno postoje. Ako se te vrijednosti postižu unutar kocke (na interioru), onda su to i lokalni ekstremi funkcije, pa su nužno stacionarne točke. Ako nisu unutra, onda moraju biti na rubu kocke.
Znači nađeš stacionarne točke na [tex]Int K=\langle -2, 2 \rangle \times \langle -2, 2 \rangle [/tex] i najveću i najmanju vrijednost na rubovima, tj. za [tex]|x|=2[/tex], [tex]|y|=2[/tex] i onda pogledaš u kojima od tih stacionarnih točaka i ovih točaka s rubova je vrijednost najveća/najmanja.
|
|
| [Vrh] |
|
Studoš
Forumaš(ica)
Pridružen/a: 07. 05. 2012. (15:14:14)
Postovi: (11)16
|
|
| [Vrh] |
|
Llama
Forumaš(ica)

Pridružen/a: 18. 10. 2012. (09:50:53)
Postovi: (14)16
Spol: 
|
|
| [Vrh] |
|
nicki minaj
Forumaš(ica)

Pridružen/a: 15. 01. 2012. (02:34:45)
Postovi: (11)16
|
 Postano: 0:36 pon, 17. 2. 2014 Naslov: Postano: 0:36 pon, 17. 2. 2014 Naslov: |
    |
|
|
Za ovogodisnji sesti:
a) izracunas da je F(4,3)=0 pa je (4,3) u S
b) F(4,3)=0, F je klace C1 i derivacija F po y u (4,3) je 15 sto nije 0, odnosno regularna matrica pa mozes primijeniti teorem za implicitno zadane funkcije i zakljuciti da postoji takva funkcija
c) od primjene teorema imas F(x,f(x))=x^2-3xf(x)+f(x)^3-7=0
deriviras po x-u i dobijes otpr 2x-3f(x)-3f'(x)+3f(x)^2f'(x)=0
dakle f'(x)=(3f(x)-2x)/(3f(x)^2-3x)
d) za svaku tocku iz S je dio uvjeta za teorem ispunjen, dakle gledas kada/da li je drugi. tu sam se dosta raspisala na kolokviju ali mislim da sam zeznula
to su barem idee
Za ovogodisnji sesti:
a) izracunas da je F(4,3)=0 pa je (4,3) u S
b) F(4,3)=0, F je klace C1 i derivacija F po y u (4,3) je 15 sto nije 0, odnosno regularna matrica pa mozes primijeniti teorem za implicitno zadane funkcije i zakljuciti da postoji takva funkcija
c) od primjene teorema imas F(x,f(x))=x^2-3xf(x)+f(x)^3-7=0
deriviras po x-u i dobijes otpr 2x-3f(x)-3f'(x)+3f(x)^2f'(x)=0
dakle f'(x)=(3f(x)-2x)/(3f(x)^2-3x)
d) za svaku tocku iz S je dio uvjeta za teorem ispunjen, dakle gledas kada/da li je drugi. tu sam se dosta raspisala na kolokviju ali mislim da sam zeznula
to su barem idee
|
|
| [Vrh] |
|
marsupial
Forumaš(ica)

Pridružen/a: 09. 01. 2012. (22:46:33)
Postovi: (63)16
Spol: 
|
|
| [Vrh] |
|
mala_narancasta
Forumaš(ica)
Pridružen/a: 26. 05. 2012. (16:38:26)
Postovi: (18)16
Spol: 
|
|
| [Vrh] |
|
gljividus
Forumaš(ica)
Pridružen/a: 10. 11. 2012. (22:18:49)
Postovi: (D)16
|
|
| [Vrh] |
|
kslaven
Forumaš(ica)

Pridružen/a: 17. 10. 2010. (18:07:06)
Postovi: (52)16
Spol: 
|
 Postano: 11:42 ned, 1. 6. 2014 Naslov: Postano: 11:42 ned, 1. 6. 2014 Naslov: |
    |
|
|
[quote="gljividus"]Bok! Jel netko moze objasniti kako riješiti zadatak kada je podrucje integracije luk logaritamske spirale r=ae^(m*fi). Od tocke A (0, a) do O (-oo, 0). Kako se dobiva jednadzba krivulje s x i y u takvim tipovima zadataka ?
Hvala puno :-)[/quote]
Pretpostavljam da se radi o zadatku 2298. iz Demidoviča...
Točku [tex]A[/tex] dobijemo za [tex]\phi=0[/tex], a točku [tex]O[/tex] možemo na početku zamijeniti točkom [tex]C=(c,ae^{mc})[/tex]. Prvo ćemo izračunati integral od [tex]A[/tex] do [tex]C[/tex], a zatim uzeti limes [tex]c\to -\infty[/tex], jer je [dtex]\lim_{c\to -\infty}C=\lim_{c\to -\infty} (c,ae^{mc})=(-\infty,0)=O.[/dtex]
Integriramo po [tex]\gamma : [0,c]\to\mathbb{R}^2[/tex], gdje je [tex]\gamma=(x,y)[/tex] za [dtex]x(\phi)=r(\phi)\cos\phi=ae^{m\phi}\cos\phi,\quad y(\phi)=r(\phi)\sin\phi=ae^{m\phi}\sin\phi.[/dtex]
| gljividus (napisa): | Bok! Jel netko moze objasniti kako riješiti zadatak kada je podrucje integracije luk logaritamske spirale r=ae^(m*fi). Od tocke A (0, a) do O (-oo, 0). Kako se dobiva jednadzba krivulje s x i y u takvim tipovima zadataka ?
Hvala puno  |
Pretpostavljam da se radi o zadatku 2298. iz Demidoviča...
Točku [tex]A[/tex] dobijemo za [tex]\phi=0[/tex], a točku [tex]O[/tex] možemo na početku zamijeniti točkom [tex]C=(c,ae^{mc})[/tex]. Prvo ćemo izračunati integral od [tex]A[/tex] do [tex]C[/tex], a zatim uzeti limes [tex]c\to -\infty[/tex], jer je [dtex]\lim_{c\to -\infty}C=\lim_{c\to -\infty} (c,ae^{mc})=(-\infty,0)=O.[/dtex]
Integriramo po [tex]\gamma : [0,c]\to\mathbb{R}^2[/tex], gdje je [tex]\gamma=(x,y)[/tex] za [dtex]x(\phi)=r(\phi)\cos\phi=ae^{m\phi}\cos\phi,\quad y(\phi)=r(\phi)\sin\phi=ae^{m\phi}\sin\phi.[/dtex]
|
|
| [Vrh] |
|
marička
Forumaš(ica)

Pridružen/a: 27. 05. 2011. (14:57:58)
Postovi: (31)16
Spol: 
|
|
| [Vrh] |
|
|















