| Prethodna tema :: Sljedeća tema |
| Autor/ica |
Poruka |
Gost
|
|
| [Vrh] |
|
Gost
|
 Postano: 0:06 čet, 16. 9. 2004 Naslov: |
    |
|
|
Nije baš zabavno, ali OK, ajmo...
Rješenje glasi:
f(x) = (1/2)*x^3 - 6*x^2 +(45/2)*x -24.
Uzme se f(x) = ax^3 + bx^2 + cx + d i iz zadanih uvjeta dobivaju se linearne jednadžbe s nepoznanicama a,b,c,d. Najbolje je krenuti od uvjeta za infleksiju, druga derivacija jednaka 0 u točki x=4, odakle 24a + 2b = 0 itd, uvrste se podaci za stacionarne točke (prva derivacija = 0) i pripadne vrijednosti funkcije, dobivaju se jednadžbe, riješe se...
Nije baš zabavno, ali OK, ajmo...
Rješenje glasi:
f(x) = (1/2)*x^3 - 6*x^2 +(45/2)*x -24.
Uzme se f(x) = ax^3 + bx^2 + cx + d i iz zadanih uvjeta dobivaju se linearne jednadžbe s nepoznanicama a,b,c,d. Najbolje je krenuti od uvjeta za infleksiju, druga derivacija jednaka 0 u točki x=4, odakle 24a + 2b = 0 itd, uvrste se podaci za stacionarne točke (prva derivacija = 0) i pripadne vrijednosti funkcije, dobivaju se jednadžbe, riješe se...
|
|
| [Vrh] |
|
Crni
Forumaš(ica)
Pridružen/a: 15. 12. 2003. (01:20:43)
Postovi: (23C)16
Spol: 
Lokacija: Zagreb
|
| Postano: 0:30 čet, 16. 9. 2004 Naslov: |
|
|
|
Kad deriviraš 2 puta polinom
[latex]f(x)=ax^{3}+bx^{2}+cx+d[/latex]
i izjednačiš sa 0 dobiješ:
[latex]\displaystyle 3ax+b=0\Longrightarrow x=-\frac{b}{3a}[/latex]
Kako točka infleksije ima apscisu x=4, slijedi da je b=-12a. Sada je
[latex]f(x)=ax^{3}-12ax^{2}+cx+d[/latex]
Deriviranjem i izjednačavanjem sa 0 gornje jednadžbe dobiješ
[latex]3ax^{2}-24ax+c=0\Longrightarrow c=24ax-3ax^{2}[/latex]
Kako je točka (3,3) lokalni ekstrem, slijedi da je c=45a. Sada je
[latex]f(x)=ax^{3}-12ax^{2}+45ax+d[/latex]
Sad uvrstiš bilo koje 2 od 3 zadane točke, npr. (3,3) i (4,2) i dobiješ sustav
[latex]54a+d=3[/latex]
[latex]52a+d=2[/latex]
Rješavanjem dobiješ a=1/2 i d=-24, pa je traženi polinom
[latex]\displaystyle f(x)=\frac{1}{2}x^{3}-6x^{2}+\frac{45}{2}x-24[/latex]
[color=red]Mislim da je jedna od navedenih točaka lokalnih ekstrema suvišna. U ovom mom slučaju minimum.[/color]
Kad deriviraš 2 puta polinom
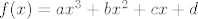
i izjednačiš sa 0 dobiješ:
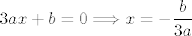
Kako točka infleksije ima apscisu x=4, slijedi da je b=-12a. Sada je
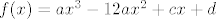
Deriviranjem i izjednačavanjem sa 0 gornje jednadžbe dobiješ
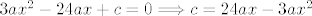
Kako je točka (3,3) lokalni ekstrem, slijedi da je c=45a. Sada je
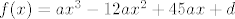
Sad uvrstiš bilo koje 2 od 3 zadane točke, npr. (3,3) i (4,2) i dobiješ sustav
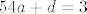
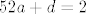
Rješavanjem dobiješ a=1/2 i d=-24, pa je traženi polinom
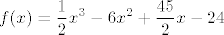
Mislim da je jedna od navedenih točaka lokalnih ekstrema suvišna. U ovom mom slučaju minimum.
|
|
| [Vrh] |
|
|
