|
Rjesenja ce biti objavljena kad i rezultati, ali ukratko za treci zadatak koji je glasio (pisem za jednu grupu, za drugu potpuno analogno):
[quote]Ortogonalne projekcije vektora
(9,0,0,0), (9,9,0,0), (9,9,9,0), (9,9,9,9)
na potprostor M unitarnog prostora R^4 su redom vektori
(1,-2,2,0), (-1,6,2,2), (1,6,10,4), (1,8,12,5).
Odredite baze za M i njegov ortogonalni komplement [latex]M^{\perp}[/latex] te izracunajte
udaljenost vektora a=(2,2,1,3) od M i [latex]M^{\perp}[/latex].[/quote]
Buduci da je ortogonalna projekcija prostora na potprostor surjektivni linearni operator (uzmemo za kodomenu taj potprostor; pogledajte sto se dogodja s vektorima koji vec leze u danom potprostoru) i da vektori (9,0,0,0), (9,9,0,0), (9,9,9,0), (9,9,9,9) razapinju R^4,
zakljucujemo da je {(1,-2,2,0), (-1,6,2,2), (1,6,10,4), (1,8,12,5)} sustav izvodnica za M. Lako se vidi da se treci i cetvrti vektor mogu zapisati preko prva dva, sto znaci da je i {(1,-2,2,0), (-1,6,2,2)} sustav izvodnica, pa zato (jer je ocito linearno nezavisan) baza za M. Bazu za ortogonalni komplement mozemo izracunati na standardni nacin, ali ovdje je jos lakse vidjeti da vektori (9,0,0,0)-(1,-2,2,0)=(8,2,-2,0) i (9,9,0,0)-(-1,6,2,2)=(10,3,-2-2) leze u [latex]M^{\perp}[/latex] (zasto?), pa kako je to potprostor dimenzije 2 (zasto?) i vektori su linearno nezavisni, zakljucujemo da je to baza za [latex]M^{\perp}[/latex].
Udaljenost vektora od potprostora je standardna stvar i trebali biste znati barem dva-tri nacina kako je izracunati.
Ipak, da jos spomenem da se ovdje mogla dobiti i formula kako ortogonalna projekcija proizvoljnog vektora na M izgleda.
Oznacimo vektore
[latex]v_1=(9,0,0,0), v_2=(9,9,0,0), v_3=(9,9,9,0), v_4=(9,9,9,9),[/latex]
a s [latex]e_1, e_2, e_3, e_4 [/latex] vektore kanonske baze od R^4.
Preslikavanje vektora u njegovu ortogonalnu projekciju na M nazovimo P. To je linearni operator, pa vrijedi:
[latex]P(e_1)=P(1/9*v_1)=1/9*P(v_1)=1/9(1,-2,2,0),[/latex]
[latex]P(e_2)=1/9*(P(v_2)-P(v_1))=1/9(-2,8,0,2),[/latex] itd.
sto daje
[latex]P(x_1,x_2,x_3,x_4)=x_1*P(e_1)+...+x_4*P(e_4)=[/latex]
[latex]
1/9(x_1-2x_2+2x_3,-2x_1+8x_2+2x_4,2x_1+8x_3+2x_4,2x_2+2x_3+x_4)[/latex]
Uvrstavanje konkretnog vektora a u gornju formulu daje jos jedan nacin za izracunati ortogonalnu projekciju a na M, duljina dobivenog vektora je udaljenost a od [latex]M^{\perp}[/latex] itd.
[b]Napomena[/b]: Nije bilo nuzno da znate da je ortogonalna projekcija (tj. tocnije ortogonalni projektor) surjektivna i linearna. Dovoljno je zakljuciti da su (1,-2,2,0) i (-1,6,2,2) u M, a (8,2,-2,0) i (10,3,-2-2) u [latex]M^{\perp}[/latex]. Buduci je suma dimenzija tih potprostora 4, zakljucujemo da su to (odnosno ti dvoclani skupovi) baze za M i njegov ortogonalni komplement.
Rjesenja ce biti objavljena kad i rezultati, ali ukratko za treci zadatak koji je glasio (pisem za jednu grupu, za drugu potpuno analogno):
| Citat: | Ortogonalne projekcije vektora
(9,0,0,0), (9,9,0,0), (9,9,9,0), (9,9,9,9)
na potprostor M unitarnog prostora R^4 su redom vektori
(1,-2,2,0), (-1,6,2,2), (1,6,10,4), (1,8,12,5).
Odredite baze za M i njegov ortogonalni komplement 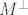 te izracunajte te izracunajte
udaljenost vektora a=(2,2,1,3) od M i 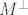 . . |
Buduci da je ortogonalna projekcija prostora na potprostor surjektivni linearni operator (uzmemo za kodomenu taj potprostor; pogledajte sto se dogodja s vektorima koji vec leze u danom potprostoru) i da vektori (9,0,0,0), (9,9,0,0), (9,9,9,0), (9,9,9,9) razapinju R^4,
zakljucujemo da je {(1,-2,2,0), (-1,6,2,2), (1,6,10,4), (1,8,12,5)} sustav izvodnica za M. Lako se vidi da se treci i cetvrti vektor mogu zapisati preko prva dva, sto znaci da je i {(1,-2,2,0), (-1,6,2,2)} sustav izvodnica, pa zato (jer je ocito linearno nezavisan) baza za M. Bazu za ortogonalni komplement mozemo izracunati na standardni nacin, ali ovdje je jos lakse vidjeti da vektori (9,0,0,0)-(1,-2,2,0)=(8,2,-2,0) i (9,9,0,0)-(-1,6,2,2)=(10,3,-2-2) leze u 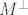 (zasto?), pa kako je to potprostor dimenzije 2 (zasto?) i vektori su linearno nezavisni, zakljucujemo da je to baza za (zasto?), pa kako je to potprostor dimenzije 2 (zasto?) i vektori su linearno nezavisni, zakljucujemo da je to baza za 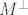 . .
Udaljenost vektora od potprostora je standardna stvar i trebali biste znati barem dva-tri nacina kako je izracunati.
Ipak, da jos spomenem da se ovdje mogla dobiti i formula kako ortogonalna projekcija proizvoljnog vektora na M izgleda.
Oznacimo vektore
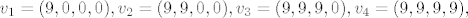
a s 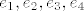 vektore kanonske baze od R^4. vektore kanonske baze od R^4.
Preslikavanje vektora u njegovu ortogonalnu projekciju na M nazovimo P. To je linearni operator, pa vrijedi:
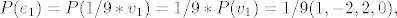
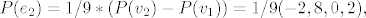 itd. itd.
sto daje
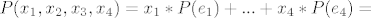
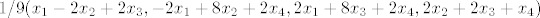
Uvrstavanje konkretnog vektora a u gornju formulu daje jos jedan nacin za izracunati ortogonalnu projekciju a na M, duljina dobivenog vektora je udaljenost a od 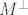 itd. itd.
Napomena: Nije bilo nuzno da znate da je ortogonalna projekcija (tj. tocnije ortogonalni projektor) surjektivna i linearna. Dovoljno je zakljuciti da su (1,-2,2,0) i (-1,6,2,2) u M, a (8,2,-2,0) i (10,3,-2-2) u 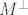 . Buduci je suma dimenzija tih potprostora 4, zakljucujemo da su to (odnosno ti dvoclani skupovi) baze za M i njegov ortogonalni komplement. . Buduci je suma dimenzija tih potprostora 4, zakljucujemo da su to (odnosno ti dvoclani skupovi) baze za M i njegov ortogonalni komplement.
|




